Should we restimate

the MAC ploidy ?

Reminder

2xMIC nuclei (2n)
- total = 4n
1xMAC nucleus (up to 800n)

if we neglict the differences in genome size :

Ratio MIC/MAC ~ 1:200

P(MIC | Paramecium DNA ) = 4 / 804

In theory:

Note:

If $p = 1/200 ^{(*)} $ :
- $P(MAC retained | IES+) \approx 50\% $
- $P(MIC | IES+) \approx 50\% $
- $P(MIC | IES+)$ depends on the MIC/MAC ploidy ratio

$\ ^{(*)} $ Quite low

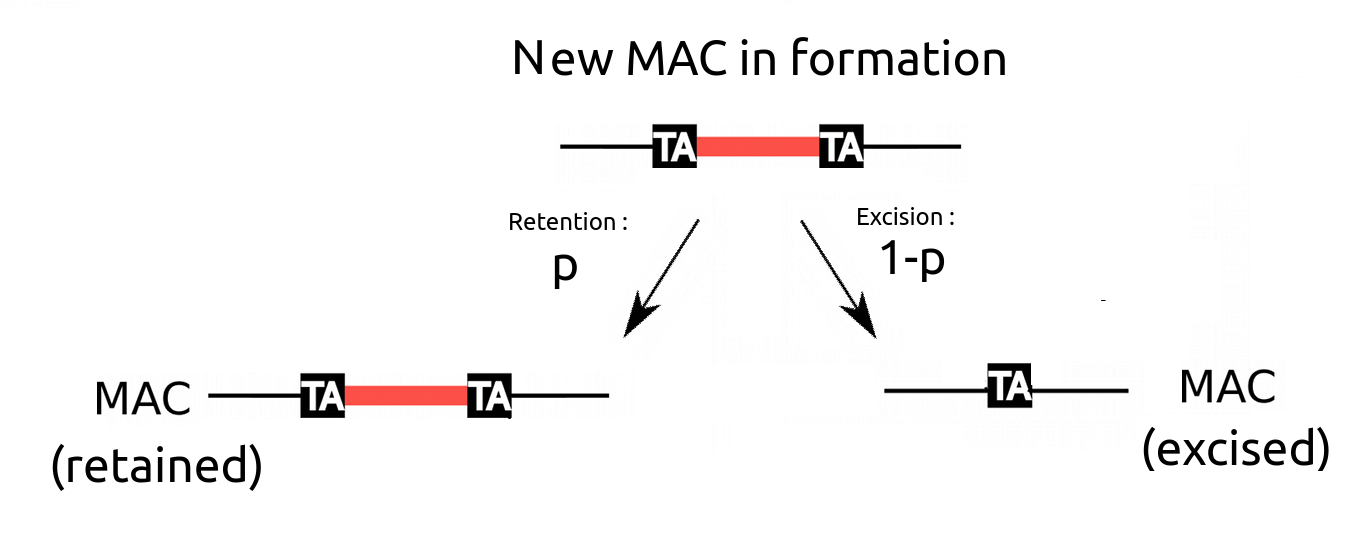
What brought us to the question of MIC/MAC ploidy ratio : The IES retention

MIC/MAC ploidy ratio: Experimental measure with NGS methods

Illumina sequencing

(total DNA)

Count the ratio of IES+ reads over the total for each bondary (left / right) of each IES

Expected 1:200 when there is no retention

Expected > 1:200 if retention

The higher the coverage, the better

Pooling of illumina

Thanks to O. Arnaiz and Eric's archeological efforts :

[ ... ]

Pooled together

> 1.000 X coverage

CTL WT

Manip 1

CTL WT

Manip 2

CTL WT

Manip 3

CTL WT

Manip 4

CTL WT

Manip

(Total DNA from WT cells)

Support left, support right, support MAC

by O. Arnaiz

(L)eft and (R)ight bondary are considered separately

the "Support MAC" overlapping a TA are common to L&R

Application issue

1 illumina sequencing : Coverage ~ hundreds X
pMIC = 4/804
High fluctuation (0, 1, 2 reads...)
Solution : Pool together several WT samples from total DNA to rise the $Np$ count

Pooled coverage $\ ^{(*)} $

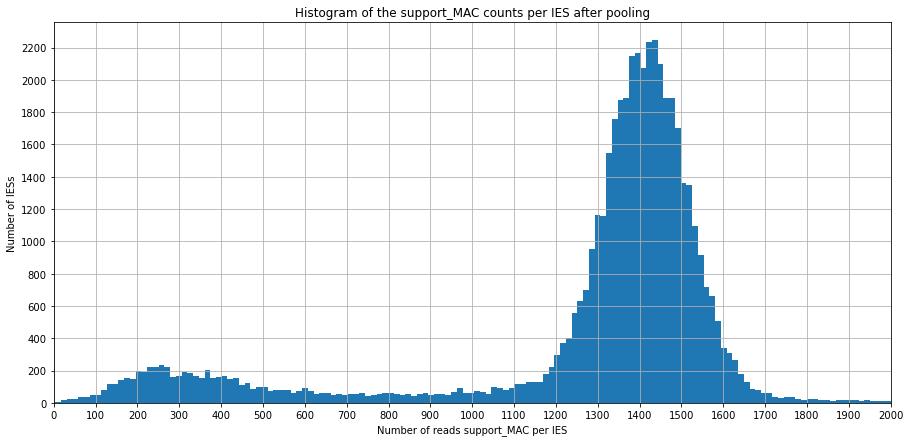
~ Variable MAC

(ploidy ratio unknown)

artifacts

(heavy tail truncated)

$\ ^{(*)} $ The number of support_MAC reads is used as a proxy to have an approximate coverage, as it represents the vast majority of reads

Area of interest because the MIC/MAC ploidy ratio can be well estimated

A routine checking that went wrong

$\ ^{(*)} $ The number of support_MAC reads is used as a proxy to have an approximate coverage, as it represents the vast majority of reads

Do we have $ \frac{nbIES+}{total\ reads} > \frac{1}{200}\ ^{(*)} \ (0.005) $ here)?

No : $ \frac{nbIES+}{total\ reads} \approx 0.00368 $

Reminder: Expected 1:200 when there is no retention

Expected > 1:200 if retention

$ \ ^{(*)} $ 4/804 $ \approx $ 1/200

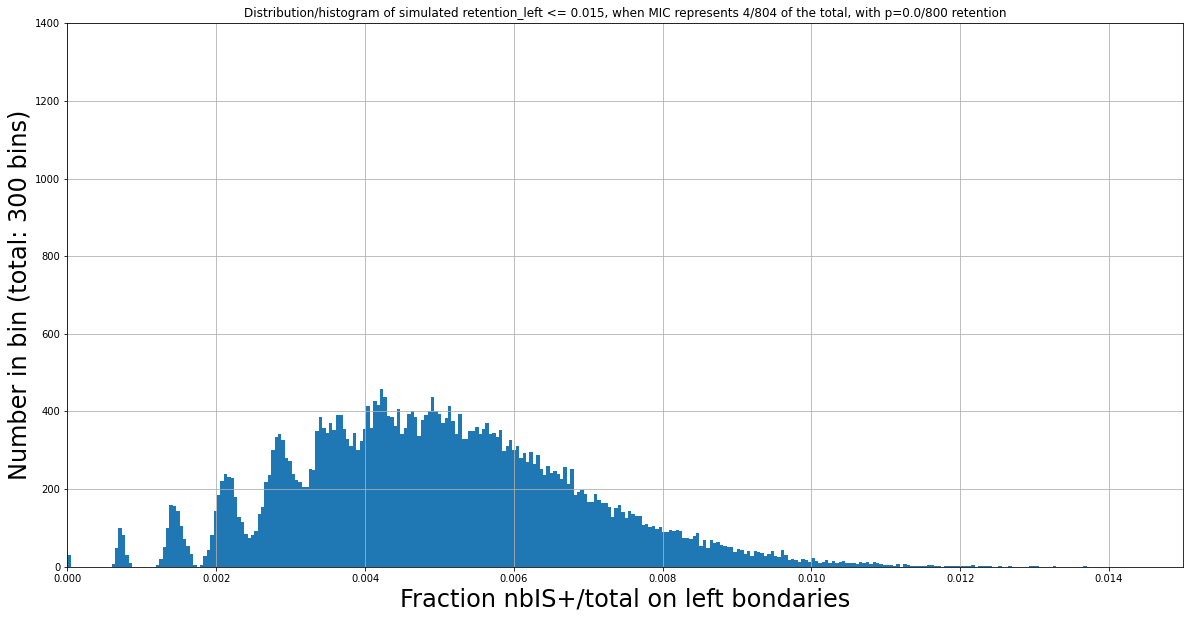
(Zoomed) Expected distribution of $\frac{nbIES+}{total\ reads} $ with Monte Carlo simulation, when P(MIC) = 4/804

If we consider

This range of coverage
p(MIC) = 4/804
retention = 0%

... Then we should expect :

Theory : 0.005 if no retention, more if retention

(Zoomed) Experimental distribution of $ \frac{nbIES+}{total\ reads} $

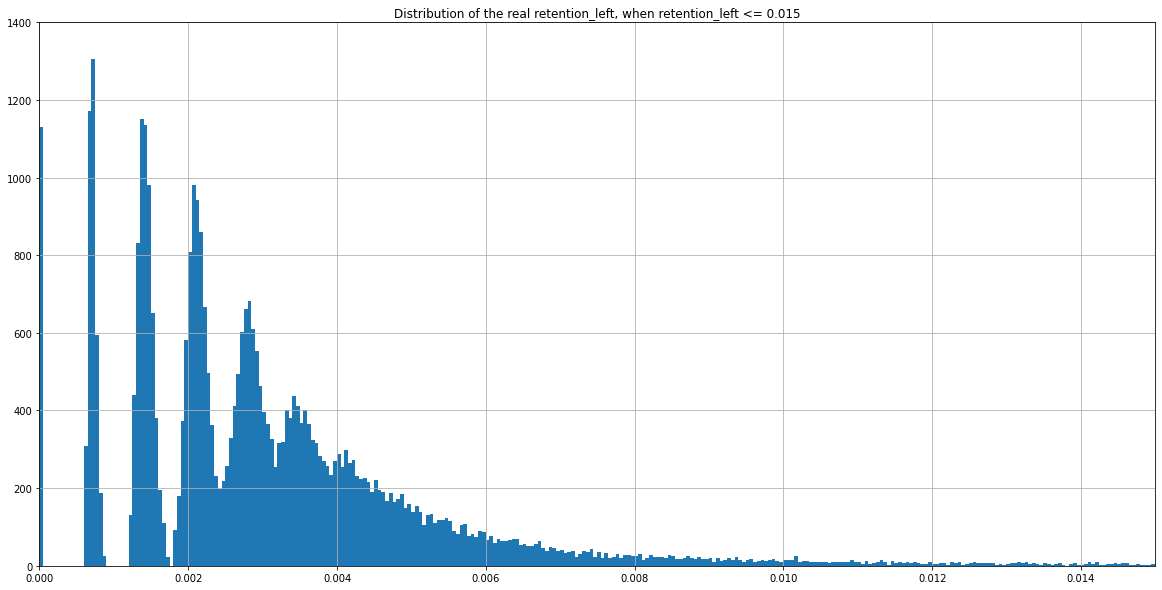
Theory : 0.005 if no retention, more if retention

Experimental distribution of $ \frac{nbIES+}{total\ reads} $

Need to zoom to see the details...

(Zoomed) Expected distribution of $\frac{nbIES+}{total\ reads} $ with Monte Carlo simulation, when P(MIC) = 4/1604

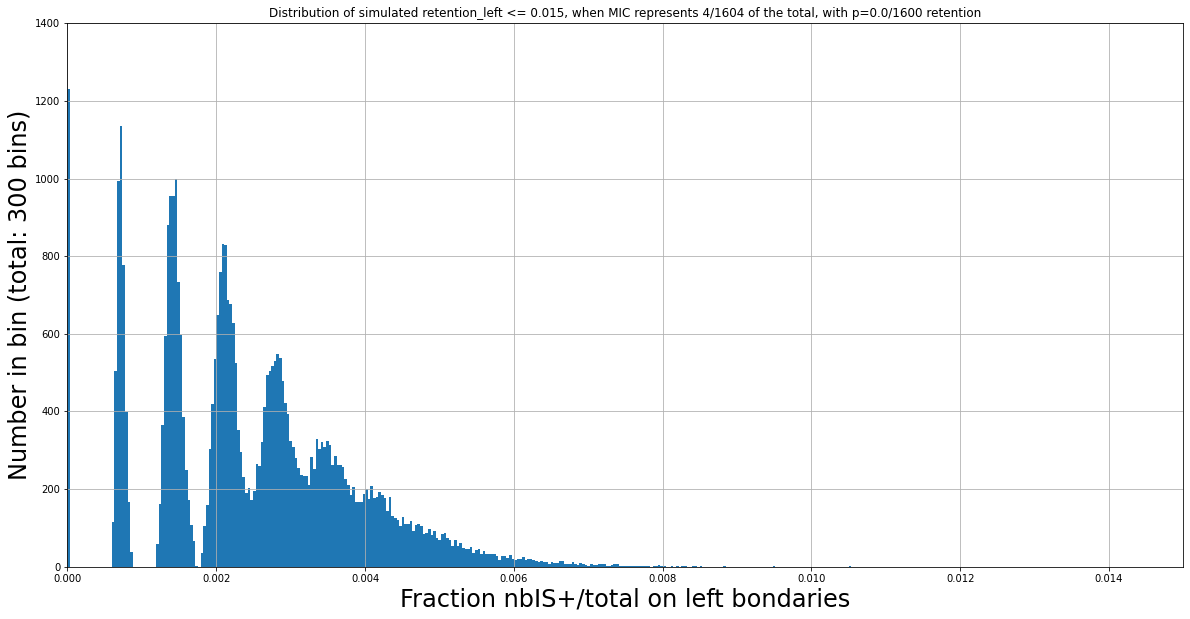
mean : 0.0025 (4/1604)

Distribution comparison (Zoom)

Monte-Carlo (4/1604)
No retention

Monte-Carlo (4/804)
No retention

Experimental

Predicted

Do we really have 4n in the MIC against 800N in the MAC, or rather against 1600N ?

What could be wrong in my approach ?

The distributions of IES+/Total we observe are still function of the retention level, even for very low fractions of IES+/total.

For instance, two expected distributions that are identical despite having different ratios MIC/MAC :

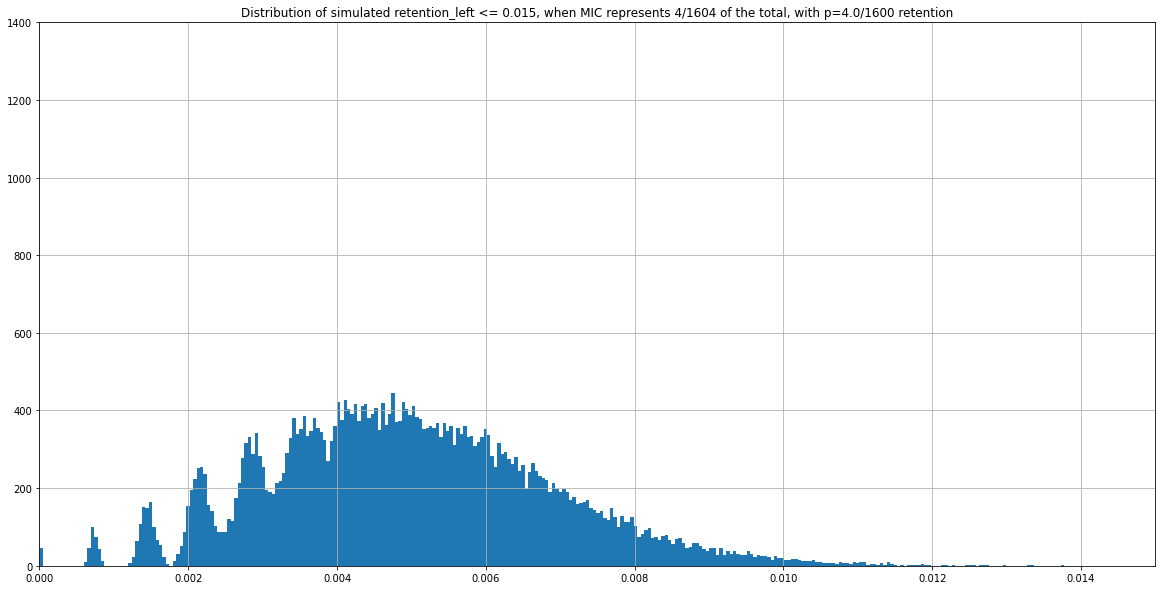
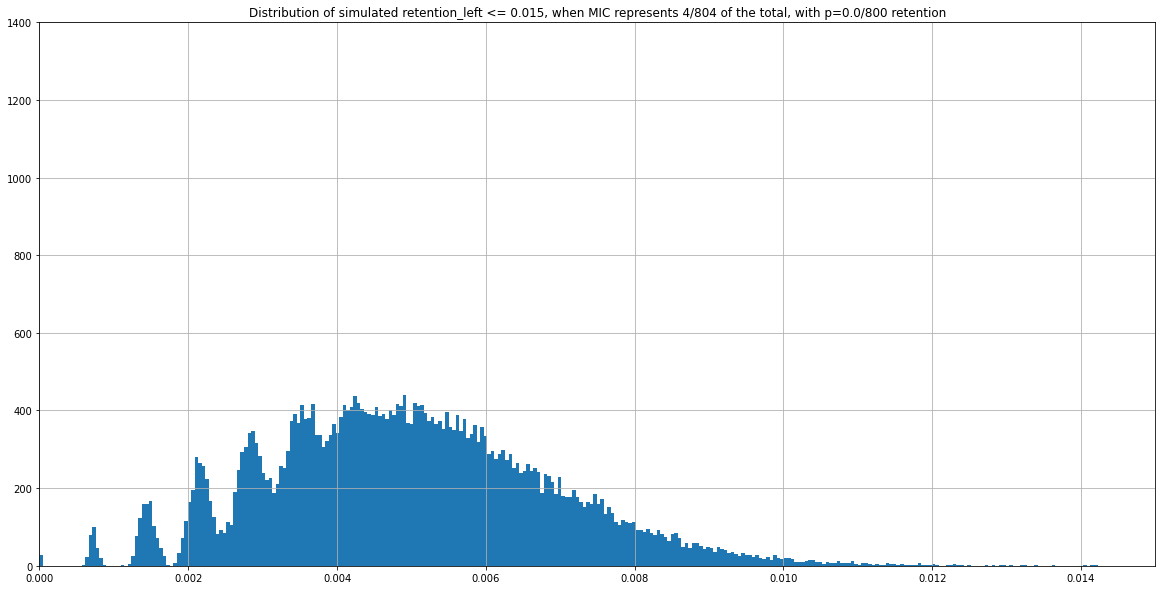
P(MIC) = 4/804

Retention = 0/800

P(MIC) = 4/1604

Retention = 4/1600

Fitness to the expectated distribution is not sufficient

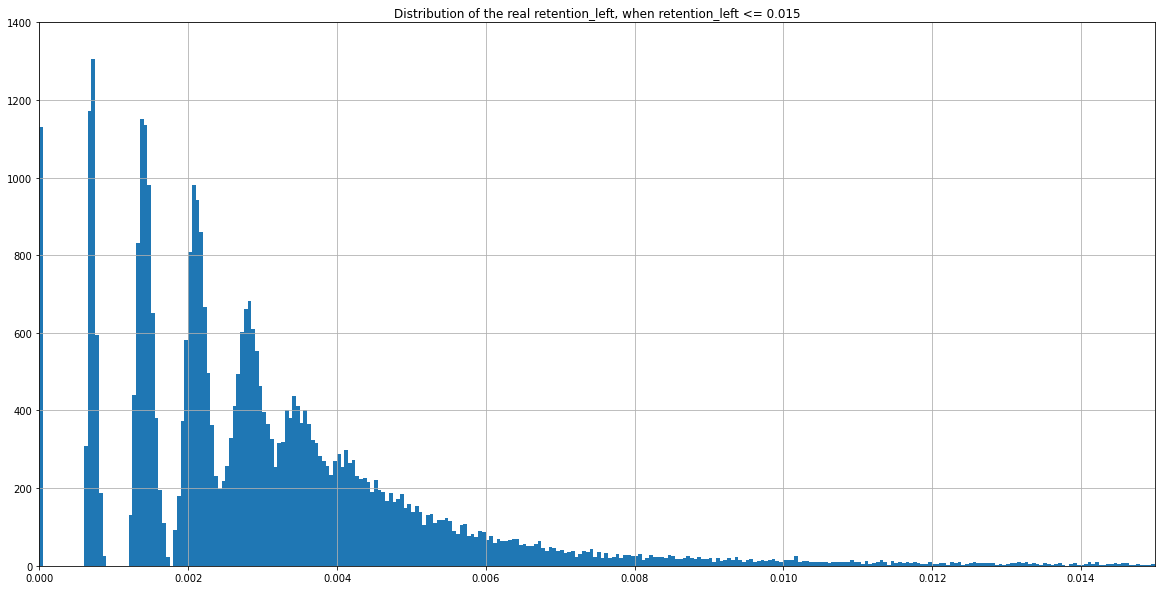
Observed

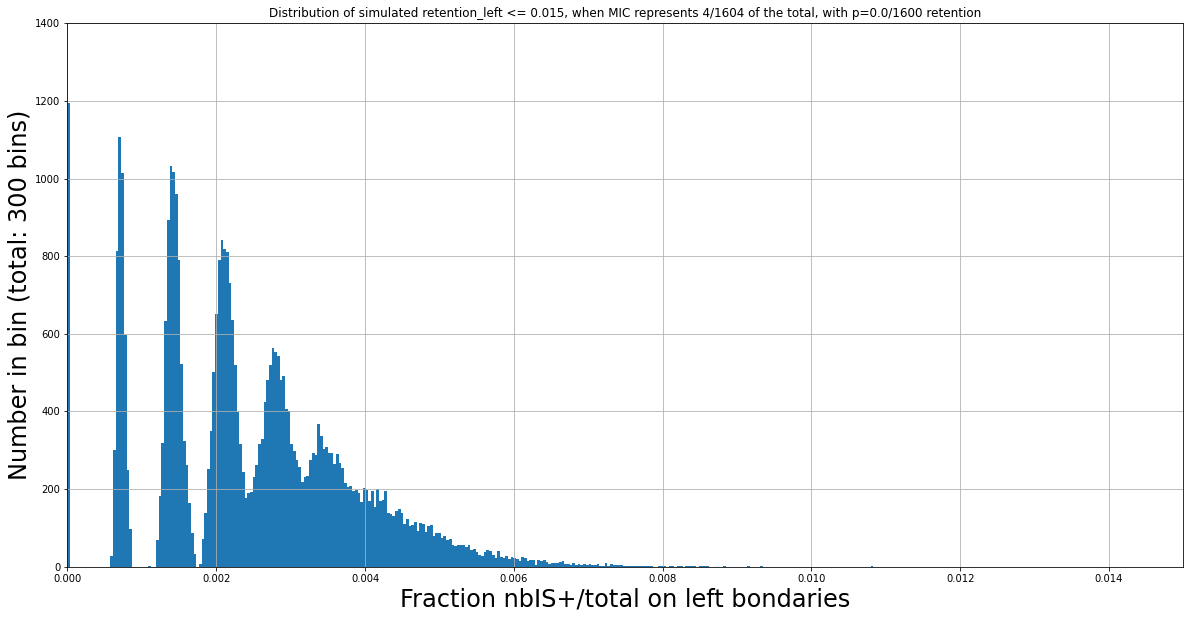
N Mac = 1600

Retention = 0/1600

N Mac = 2000

Retention = 1/2000

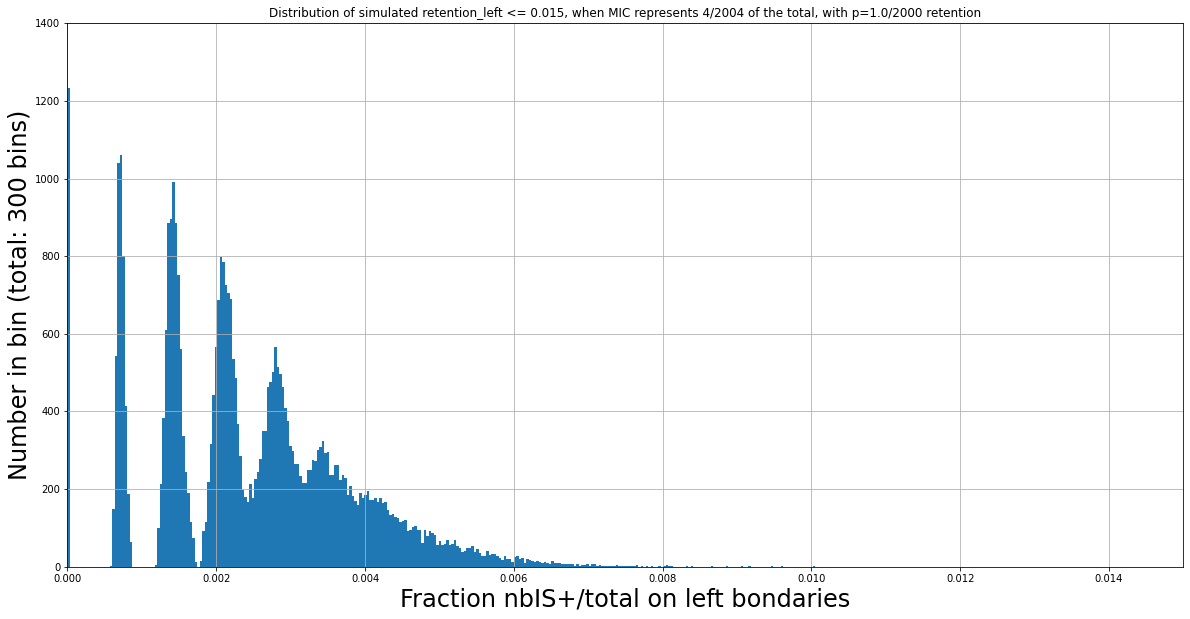
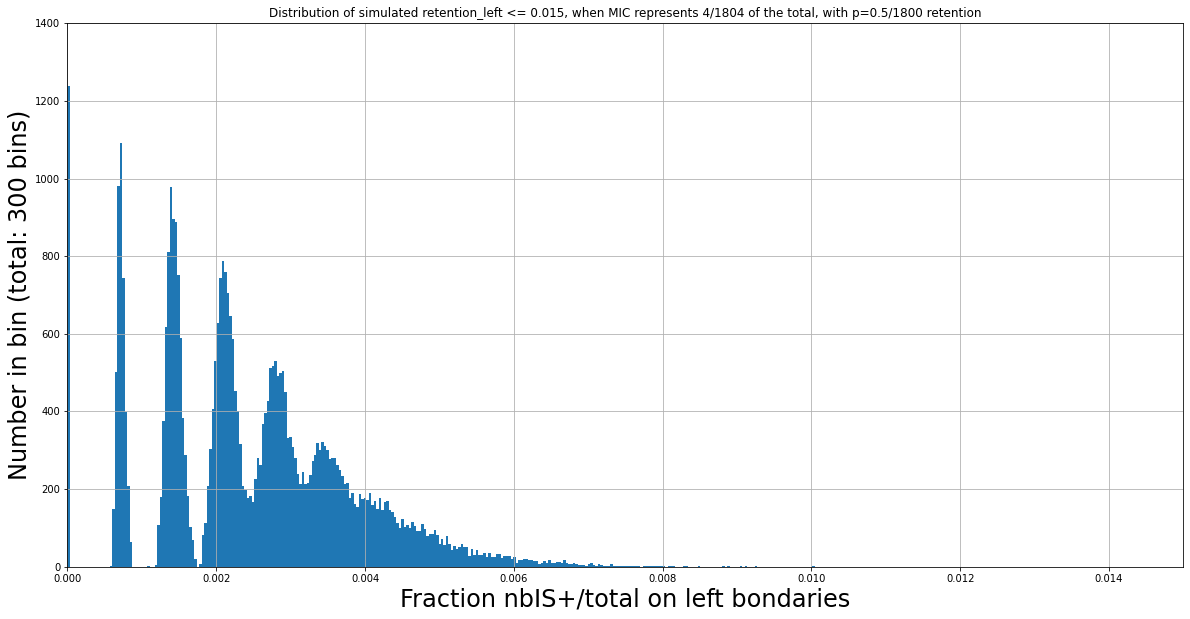
N Mac = 1800

Retention = 0.5/1800

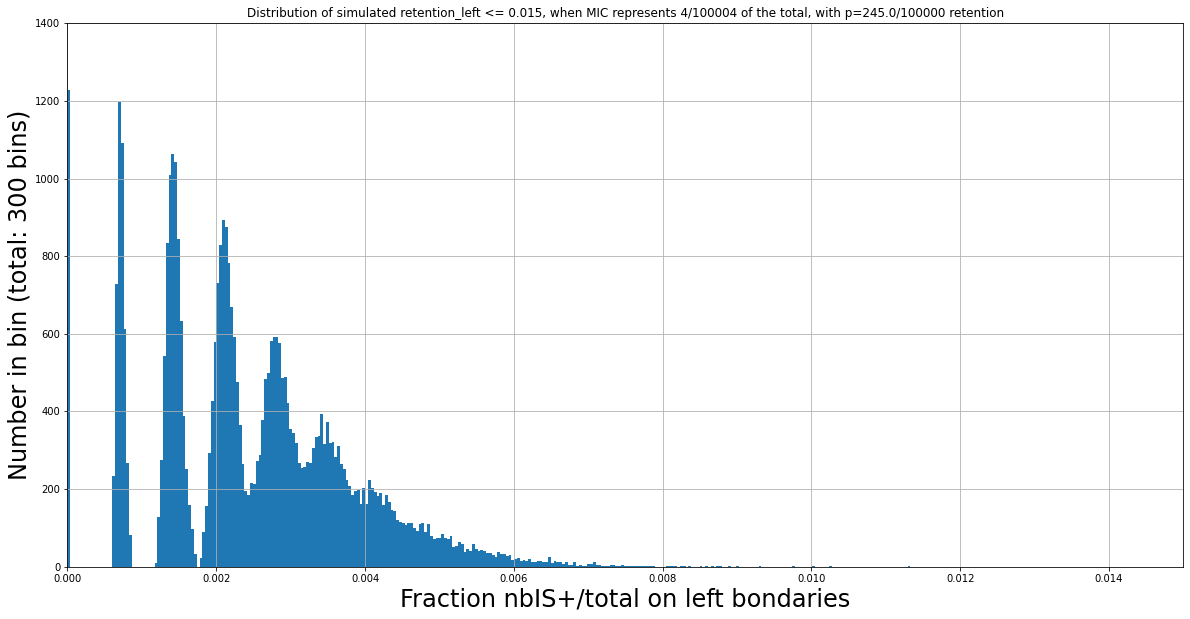
N Mac = 100000

Retention = 245/100000

(absurd)

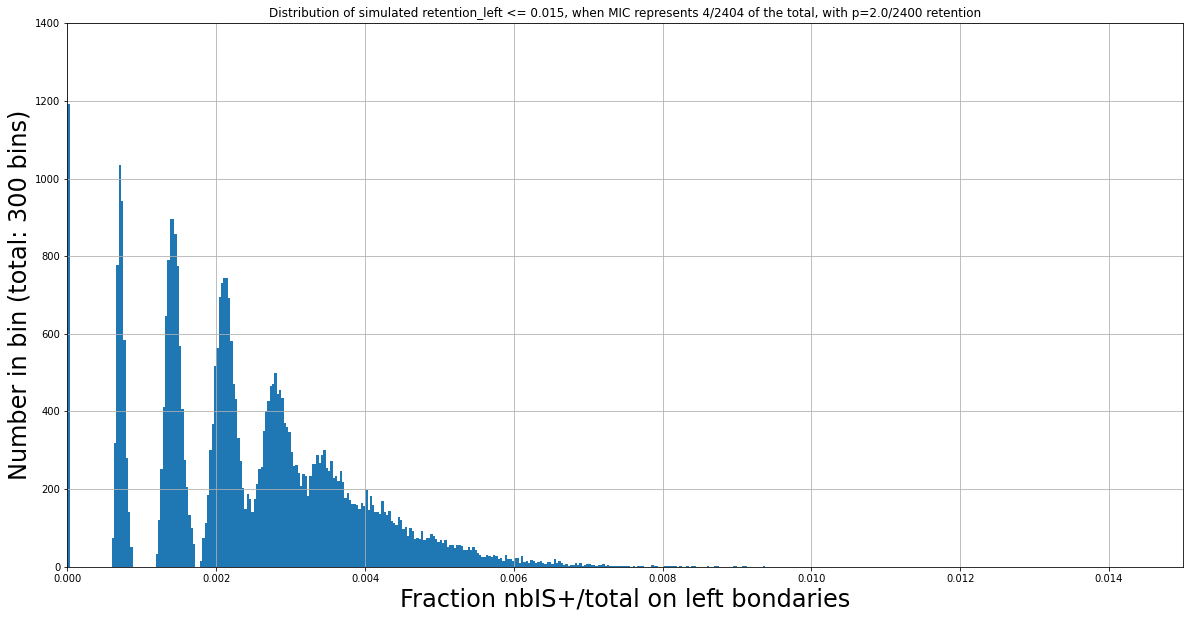
N Mac = 2400

Retention = 2/2400

Why is the ploidy ratio likely not 4:800 ?

Despite the considerations of the previous slide,

No retention level (ranging from 0/800 to 800/800) can possibly lead anywhere close to this figure (obtained from experimental data) while having a MIC/MAC 4:800

Other considerations

The pipeline to assign the reads at left and right bondary is stringent. What if a few are lost ?
The MIC and MAC genomes actually don't have the same size, so we already know that 4:800 is not a correct number
The ploidy could vary from one chr to another
All IESs don't have the same probability p of being retained, contrary to our model. The reality is likely much more complex
The possibilities are actually way more diverse than a simple choice between 4:800 or 4:1600. There is an infinity of combinations of couples (ploidy ratio,retentions) that could fit approximately what we observe. None of them is 100% satisfying.

Conclusion

4:800 ? 4:1600 ?

Anything else ?

I am naked in the darkness of ignorance

Score de rétention

\frac{nb\ IES^+}{N} = Retention\ score

Rationnel de base:

Attendu sans rétention ~ 1/200
L'observé est-il nettement supérieur à ~1/200 ?

Si N = reads passant sur la jonction TA du MAC + les reads portant l'IES :

A priori: Simple, efficace, pas cher.

Implémentation stat

= Comparaison de proportion: théorique $p$ VS observée $p_0$

$$ H_0 : p = p_0 $$

$$ H_1 : p > p_0 $$ (unilatérale droite)

$$ pvalue = P(p_0 | H_0) $$

Faisable uniquement si:

$$ N \geq 30,\ N\cdotp_0\geq5\ et\ N(1-p_0)\geq5 $$

Très souvent faux pour nous

Option 1 : Approximation loi normale.

Option 2 : Test exact de Fisher

Distribution des p-values

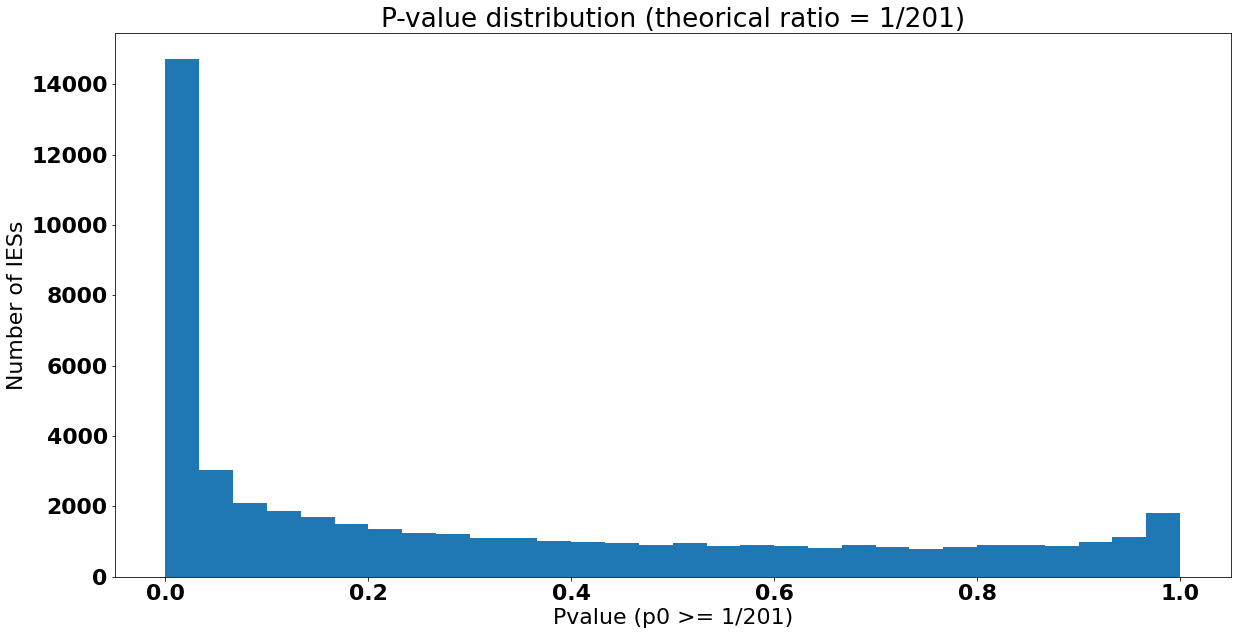
$$ pvalue \leq 5\% \iff Retention \geq 0.00848 $$

Premier non rejet de $H_0$

La molécule avec le score de rétention le plus élevé pour laquelle $H_0$ n'est pas rejetée pour $ \alpha = 5\% $ :

Reads MAC : 70

Reads IES+ : 2

$p_0= 0.02857... $

$ Retention = \frac{2}{72} = 0.27..7 $

> Si on se base hâtivement sur le test, on considérera que ça vient physiquement du MIC

Pourtant...

Reads MAC : 70

Reads IES+ : 2

$p_0= 0.02857... $

$ Retention = \frac{2}{72} = 0.27..7 $

Si la probabilité réelle de rétention de cette IES dans le MAC notée $ P(R|MAC) $ était, par exemple, de 1% :

Il n'y aurait rien de choquant à n'avoir 0 read IES+ venant du MIC quand on sait que leur probabilité est de ~1/201 du total.
Il n'y aurait rien de choquant à avoir 2 reads IES+ qui viennent du MAC avec une probabilité de 1/100 par molécule MAC
Les deux IES+ qu'on aurait piochées ici viendraient très probablement du MAC retenu

Plus précisément : $ P(MIC|IES^+) = 50\%) $
Peut-on considérer que c'est suffisant pour étudier le MIC ? ...

Solution évidente :

> Prendre $ \alpha $ plus grand !

Quel threshold ?
Sur quelle base ?
On va très vite tout éliminer

Soulève d'autres problèmes :

Autre formulation de la situation :

Si $pvalue \leq \alpha $ : clairement retenues
Si $pvalue > \alpha$, ça peut parfaitement être rempli de séquences retenues quand même.

Or, on veut travailler sur les IES avec $pvalue > \alpha$...

Conclusion : Le score de rétention n'est pas une métrique appropriée pour notre problème.

Reformulation

Ce qui nous intéresse est uniquement, pour chaque IES :

$ P(MIC|IES^+) $ pour chaque IES
Le score de rétention n'en est qu'un proxy

Idée grossière:

On ne connait pas le pourcentage de molécules MAC qui retiennent l'IES. Mais :

On connait le nombre d'IES+ obtenu
On connait le nombre de MIC espéré: $ nb_{MIC} \approx P(MIC) \cdot N $
On a donc une idée de l'attendu du nombre de séquences MAC retenant l'IES : $ E( nb_{MACret} ) \approx {nbIES}^+ - E( nbMIC ) $

De là : On a bien une piste pour estimer la proportion des IES+ qui viennent physiquement du MIC:

Exemple :

10.000 reads
dont 5000 reads IES+

--> On peut estimer grossièrement $ P(R|MAC) \approx 50\% $

$ P(MIC |IES⁺) \approx \frac{1}{200} $

Exemple guide

Exemple guide :

N = 100

$ nb_{IES^+} = 3 $

$ P(MIC) = \frac{4}{804} $

P(retention) = ??

$ P(MIC|IES⁺) = ?? $

Calcul des probabilités :

On a donc, littéralement, la distribution de probabilité de la variable aléatoire $ \frac{nbMIC}{nbIES+} $ sachant nbIES+.
$ P(MIC|IES+) $ est approché par la moyenne de cette variable aléatoire.

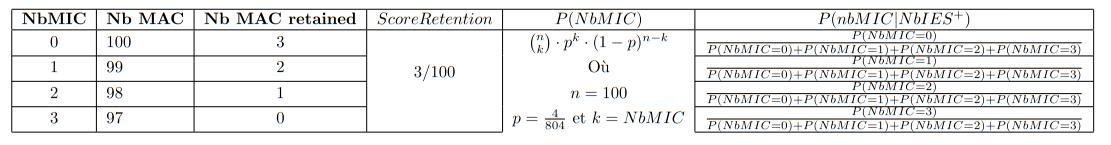
> Pour une IES donnée, on peut donc estimer la probabilité qu'elle vienne du MIC ou du MAC

On peut utiliser cet estimateur en déduire, pour un ensemble de X séquences $IES^+$, quel sera, en moyenne, la proportion de molécules venant du MIC.

$ \frac{nbMIC}{NbMacRet} $

0/3

1/3

2/3

3/3

Should we restimate

the MAC ploidy ?

Reminder

What brought us to the question of MIC/MAC ploidy ratio : The IES retention

MIC/MAC ploidy ratio: Experimental measure with NGS methods

Pooling of illumina

Support left, support right, support MAC

by O. Arnaiz

Application issue

Pooled coverage \(\ ^{(*)} \)

A routine checking that went wrong

(Zoomed) Expected distribution of \(\frac{nbIES+}{total\ reads} \) with Monte Carlo simulation, when P(MIC) = 4/804

(Zoomed) Experimental distribution of \( \frac{nbIES+}{total\ reads} \)

Experimental distribution of \( \frac{nbIES+}{total\ reads} \)

(Zoomed) Expected distribution of \(\frac{nbIES+}{total\ reads} \) with Monte Carlo simulation, when P(MIC) = 4/1604

Distribution comparison (Zoom)

What could be wrong in my approach ?

Why is the ploidy ratio likely not 4:800 ?

Other considerations

Conclusion

Score de rétention

Implémentation stat

Distribution des p-values

Premier non rejet de \(H_0\)

Pourtant...

Solution évidente :

Autre formulation de la situation :

Reformulation

Idée grossière:

Exemple guide