Particle Filter for Identifying and Correcting Phase Transitions in Semi-Coherent GNSS Signals

Brian Breitsch      Jade Morton

University of Colorado Boulder

ION GNSS+ 2019

Semi-Coherent Signals:

  • random short-delay multipath in the presence of a dominant direct signal
  • adverse impact on carrier phase measurement
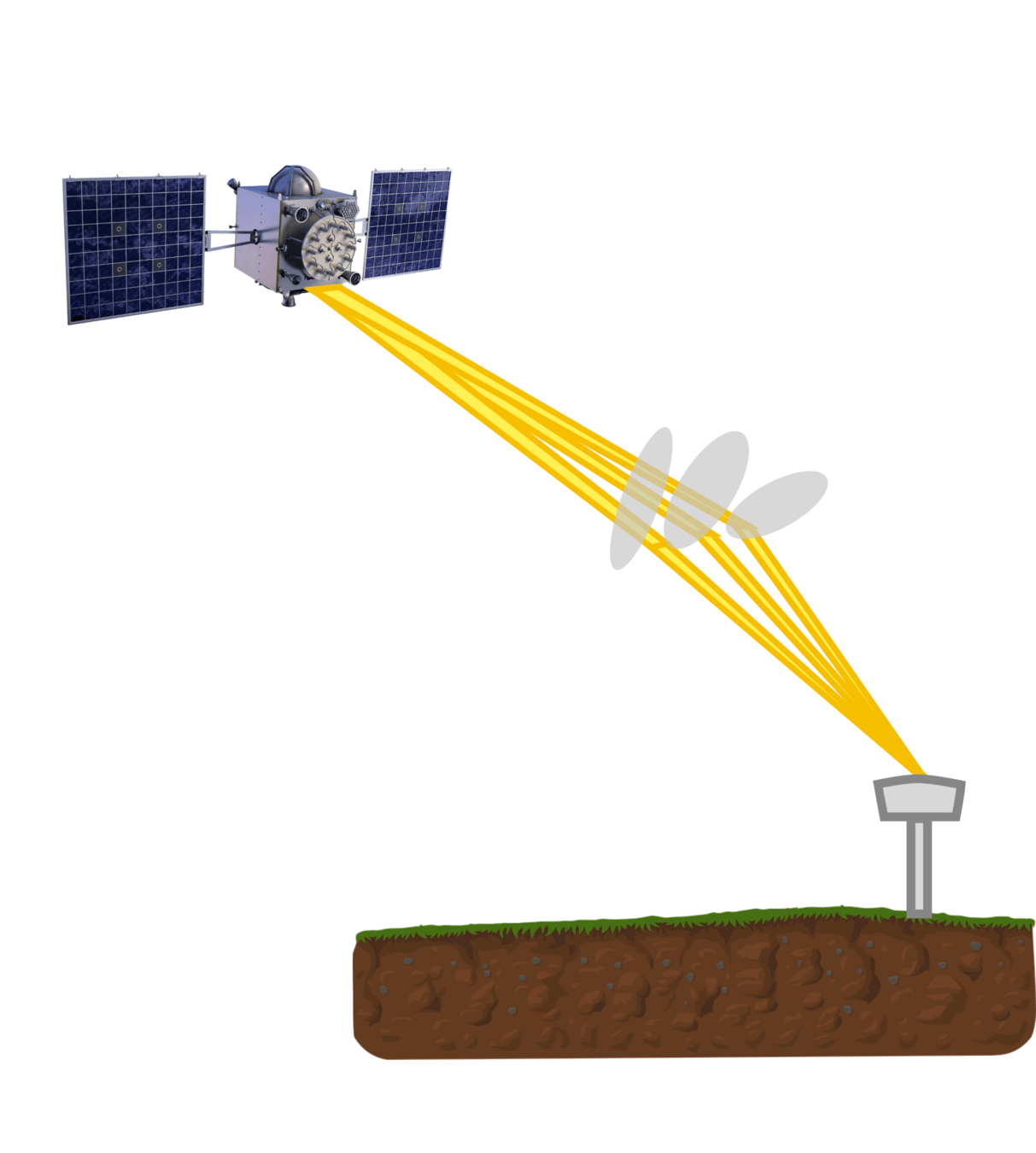
  • particularly prevalent in remote-sensing applications

ionosphere scintillation

radio occultation / troposphere scintillation

ocean reflection

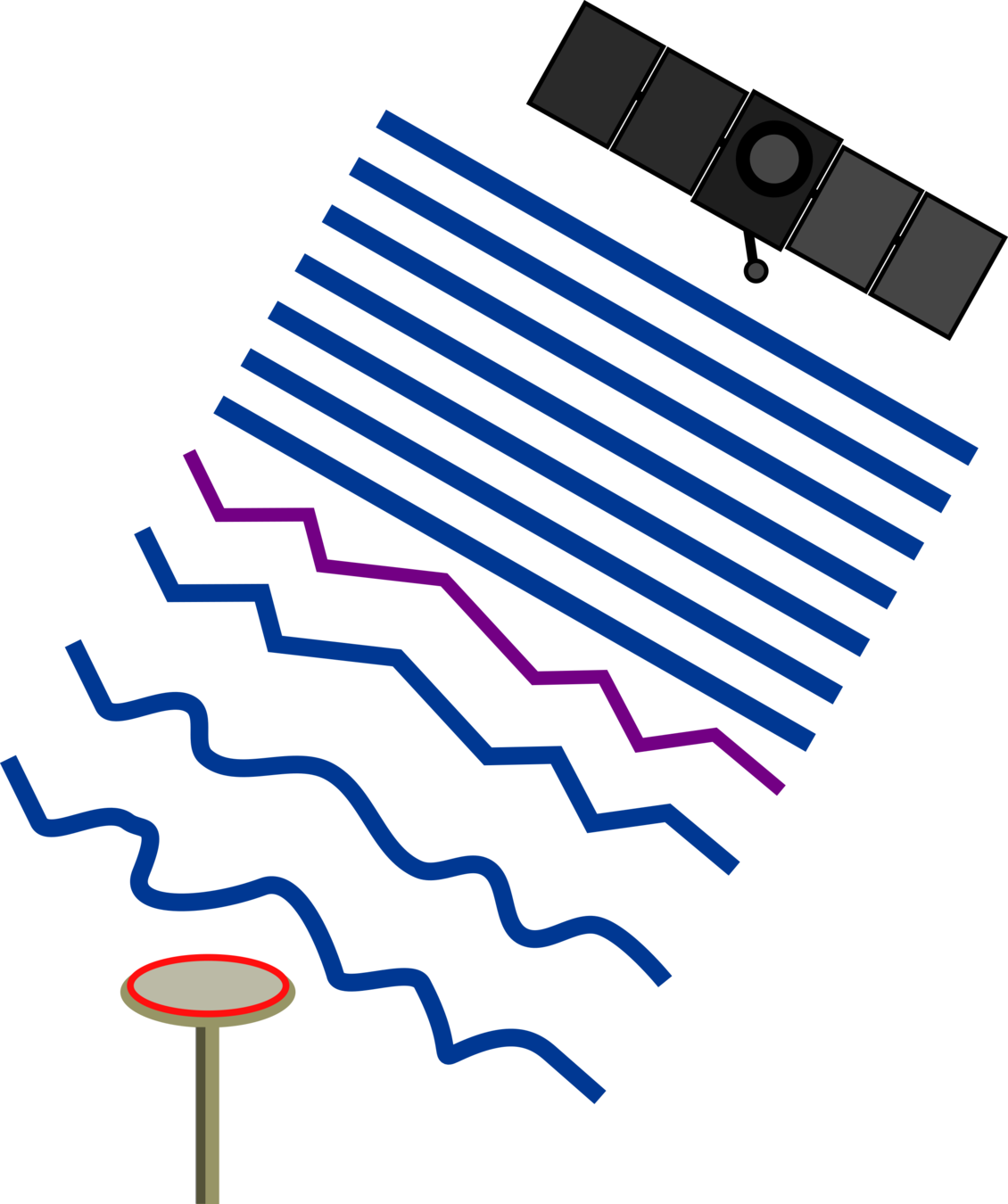
Motivation: Semi-Coherent Examples

Problem: Phase Transitions

Solution: Particle Filter Algorithm

Background: Signal Model

Semi-Coherent Signals:

Ionosphere Scintillation (Ascension Island)

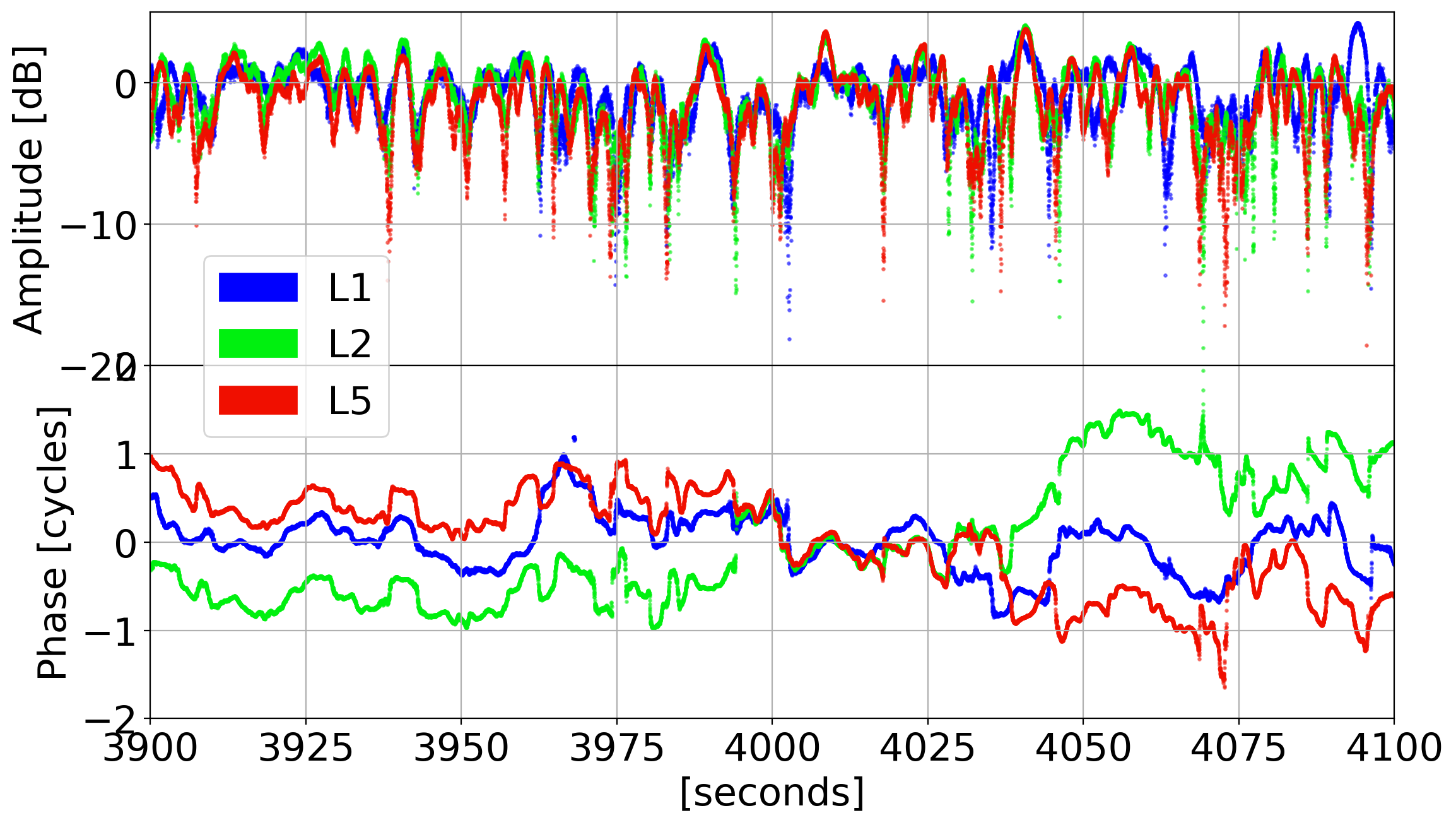
Semi-Coherent Signals:

Troposphere Scintillation (Hawaii)

Semi-Coherent Signals:

Ocean Reflection (Hawaii)

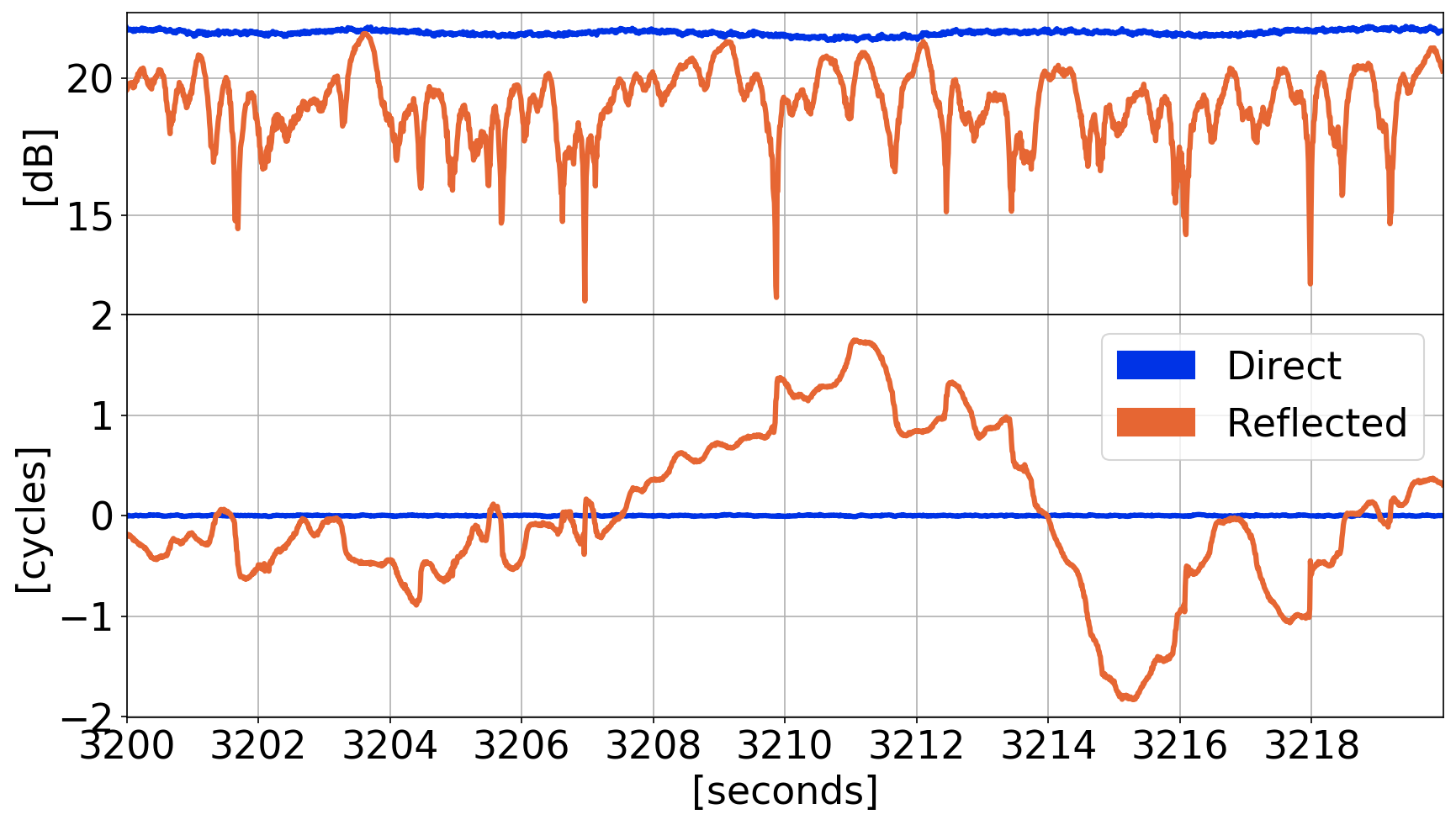
GPS L1 (PRN 30)

Motivation: Semi-Coherent Examples

Problem: Phase Transitions

Solution: Particle Filter Algorithm

Background: Models

Signal Model

REFRACTIVE IONOSPHERE  EFFECT

MULTIPATH PHASE EFFECT

FREQUENCY INDEPENDENT EFFECTS

A_k\exp(i\phi_k)
\frac{\lambda_k}{2\pi} \phi_k= G + \alpha_k T + \frac{\lambda_k}{2\pi}\tilde{\phi}_k
M_k = \tilde{A}_k\exp(i\tilde{\phi}_k)

phase model

baseband signal

multipath model

A = \tilde{A}

Assume normalized signal power; amplitude measurements are direct measurements of \(\tilde{A}\)

State-Space Model

\mathbf{x} = \begin{bmatrix} G \\ T \\ \tilde{\phi}_{L1} \\ \tilde{\phi}_{L2} \\ \tilde{\phi}_{L5} \\ \tilde{A}_{L1} \\ \tilde{A}_{L2} \\ \tilde{A}_{L5} \end{bmatrix}

state

% \mathbf{y} = \begin{bmatrix} \phi_{L1} \\ \phi_{L2} \\ \phi_{L5} \end{bmatrix} = H \mathbf{x} \mathbf{y} = H\mathbf{x} = \begin{bmatrix} \phi_{L1} \\ \phi_{L2} \\ \phi_{L5} \\ A_{L1} \\ A_{L2} \\ A_{L5} \end{bmatrix} + \mathbf{\epsilon}

measurements

Multipath Model

M_k = \tilde{A}_k\exp(i\tilde{\phi}_k)

coherent multipath

weak scintillation

strong scintillation

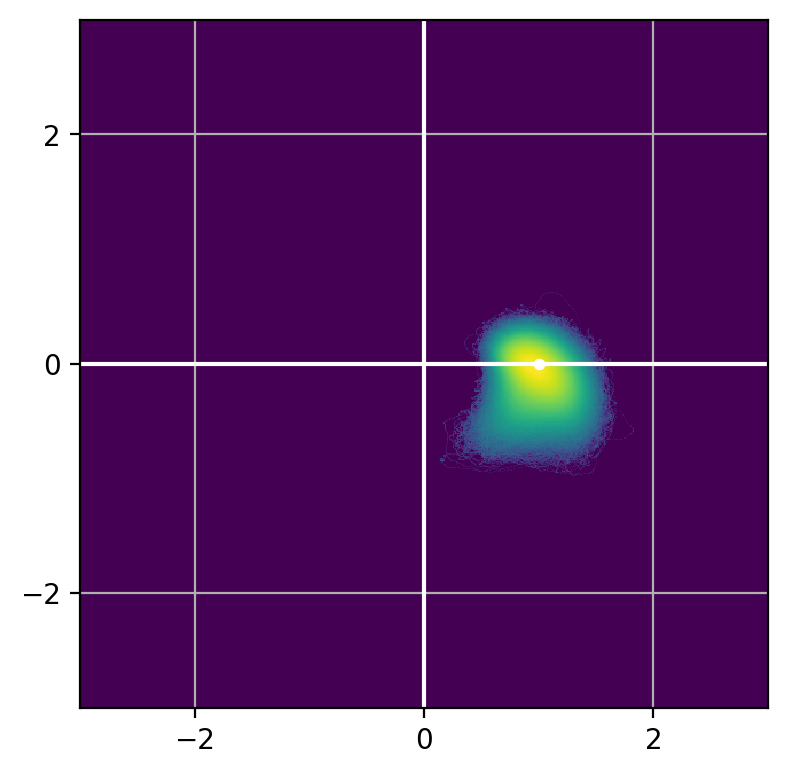
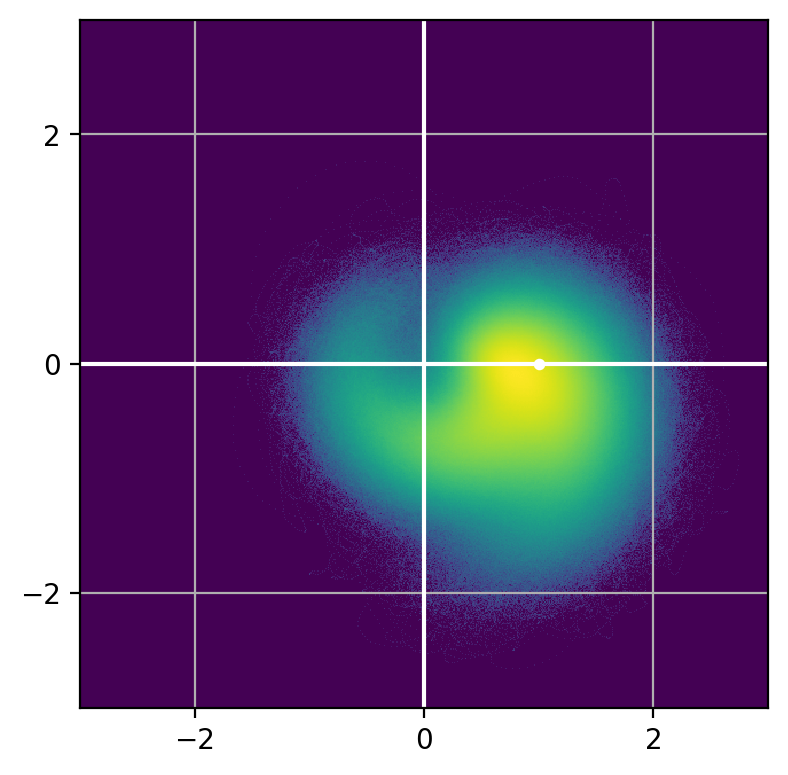
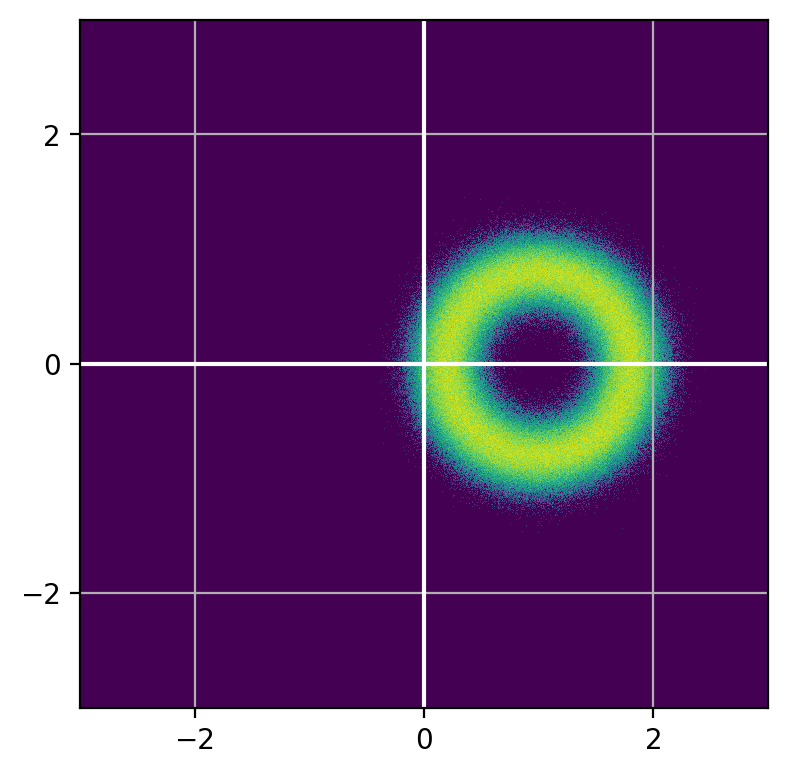
Whether deterministic or stochastic, we can model \(M\)

Re

Im

Scintillation Simulator

  • multi-frequency scintillation simulator using physics-based phase screen model

We use this example to test the particle filter algorithm

Jiao, Y., Xu, D., Rino, C. L., Morton, Y. T., & Carrano, C. S. (2018). A Multifrequency GPS Signal Strong Equatorial Ionospheric Scintillation Simulator: Algorithm, Performance, and Characterization. IEEE Transactions on Aerospace and Electronic Systems, 54(4), 1947-1965.

Motivation: Semi-Coherent Examples

Problem: Phase Transitions

Solution: Particle Filter Algorithm

Background: Signal Model

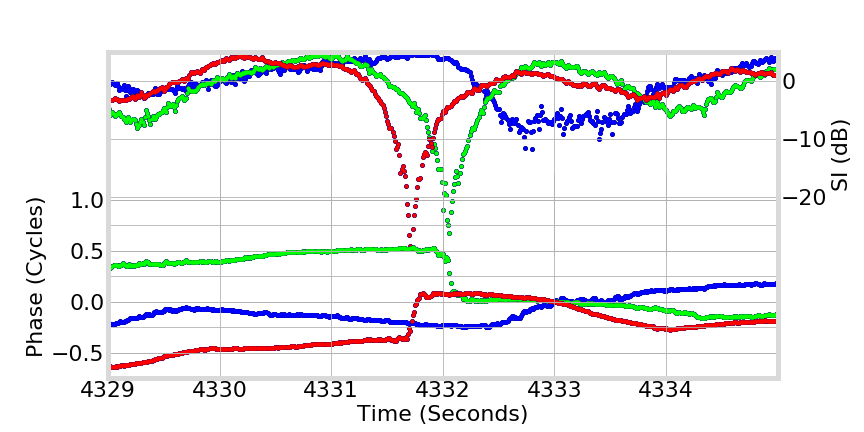
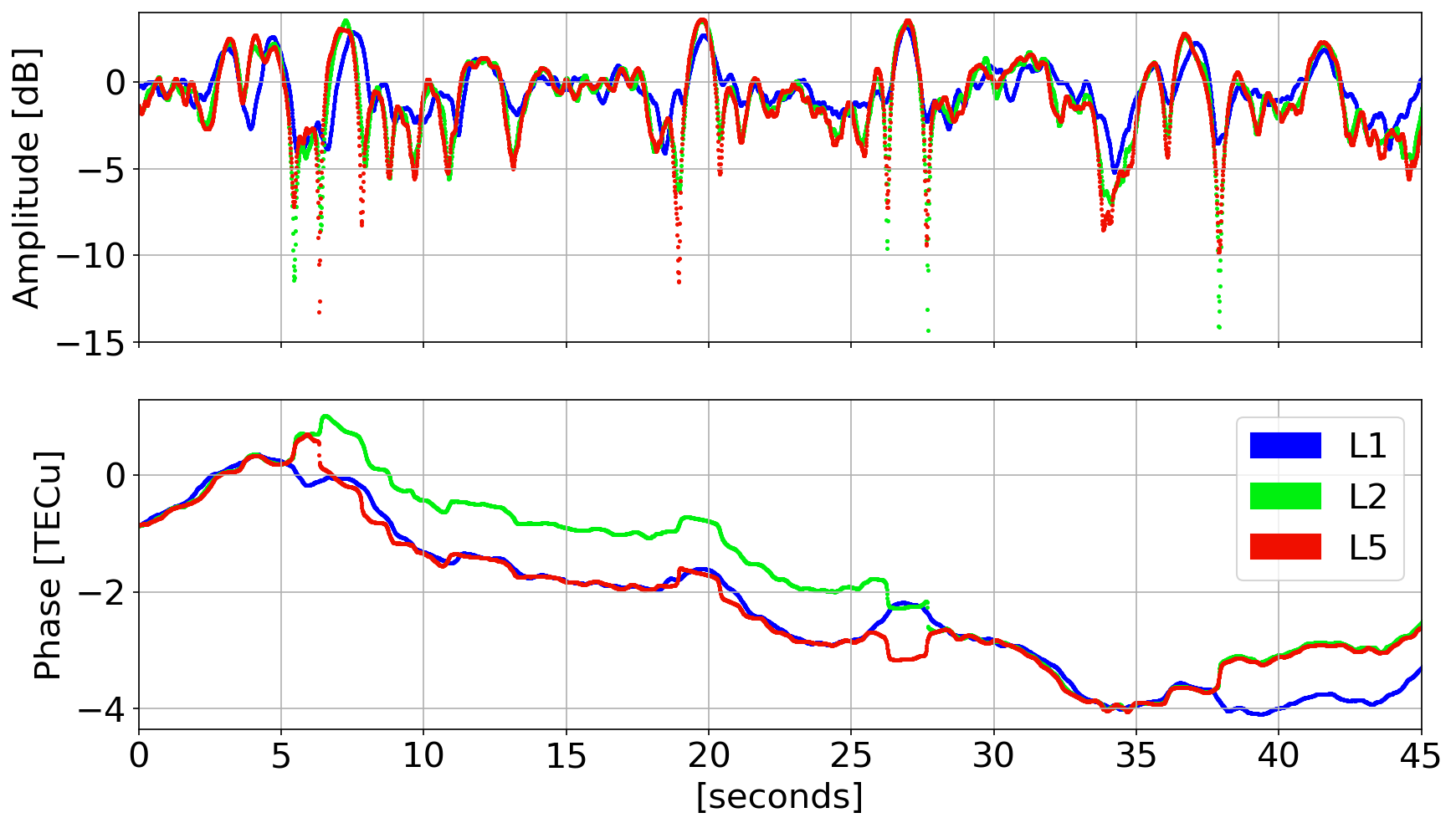
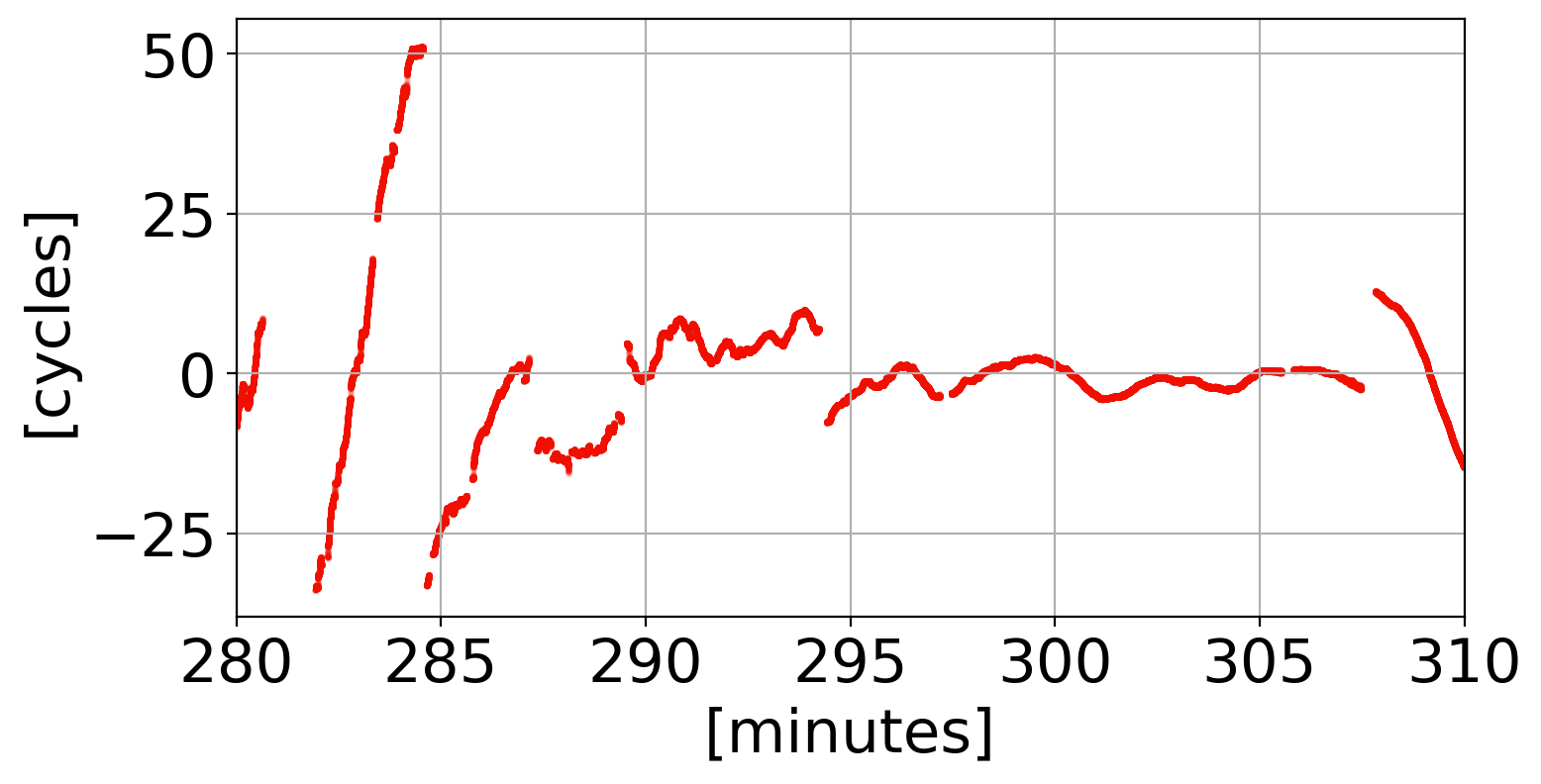
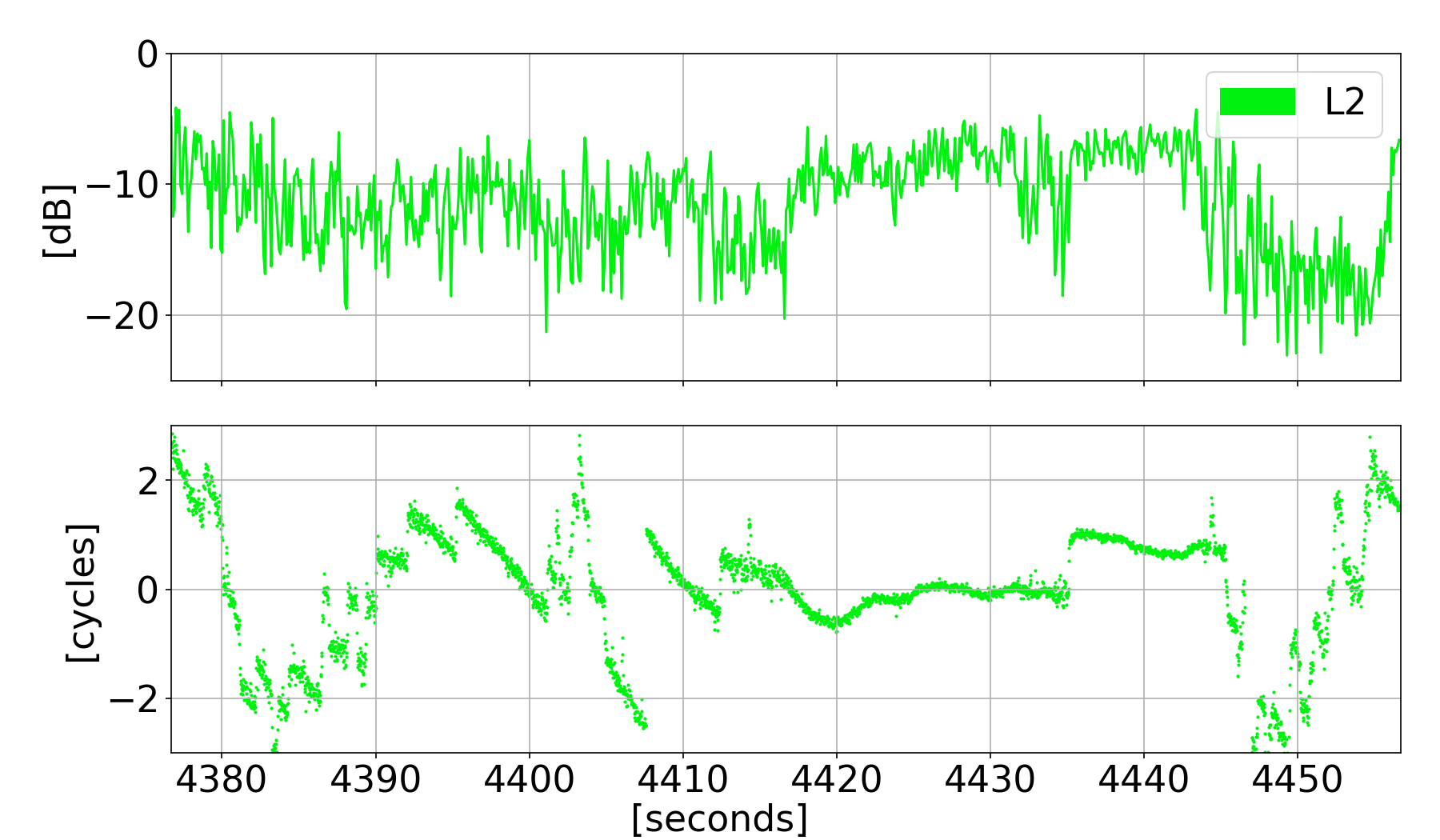
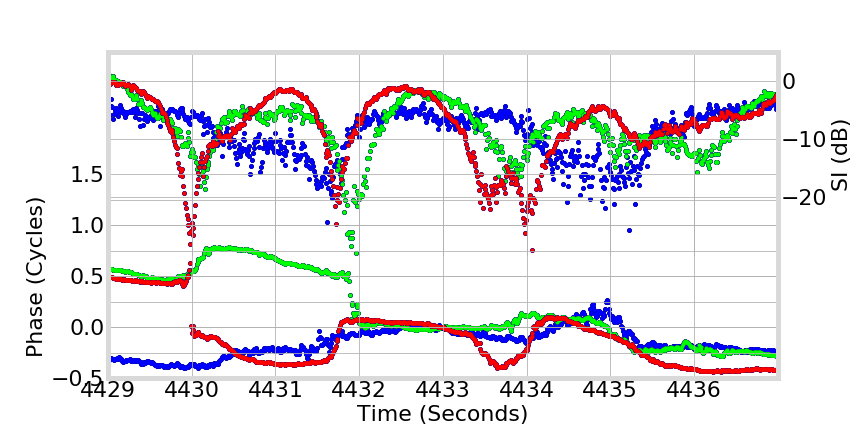
Phase Transitions

not instantaneous!

difficult to discriminate occurrence!

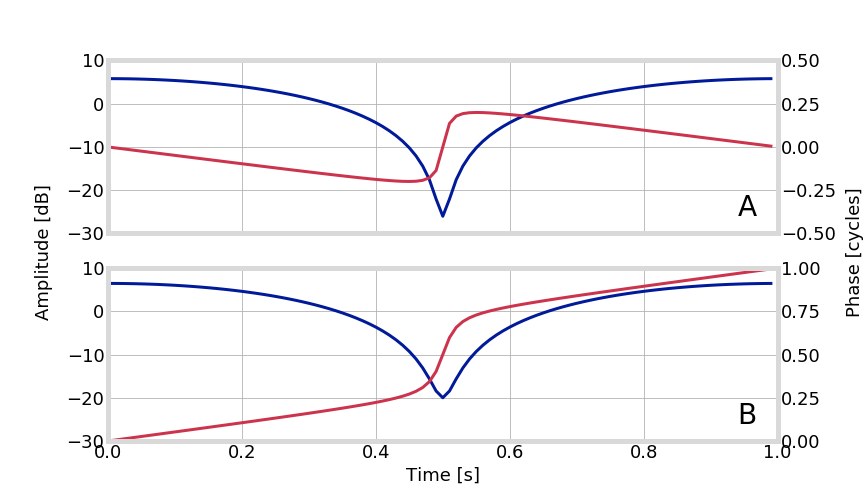
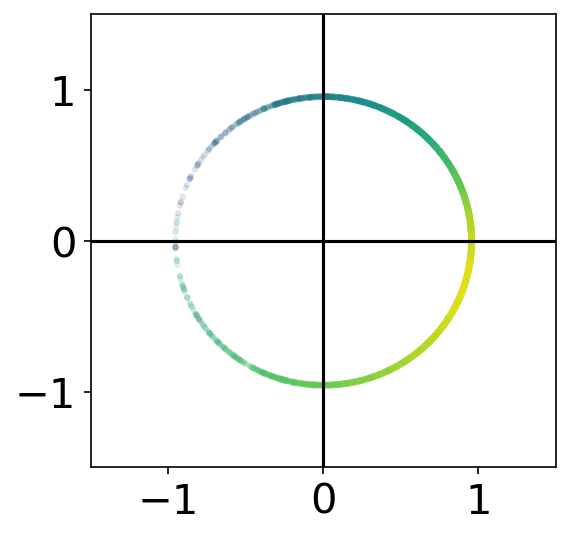
  • singularity at origin causes phase bifurcation

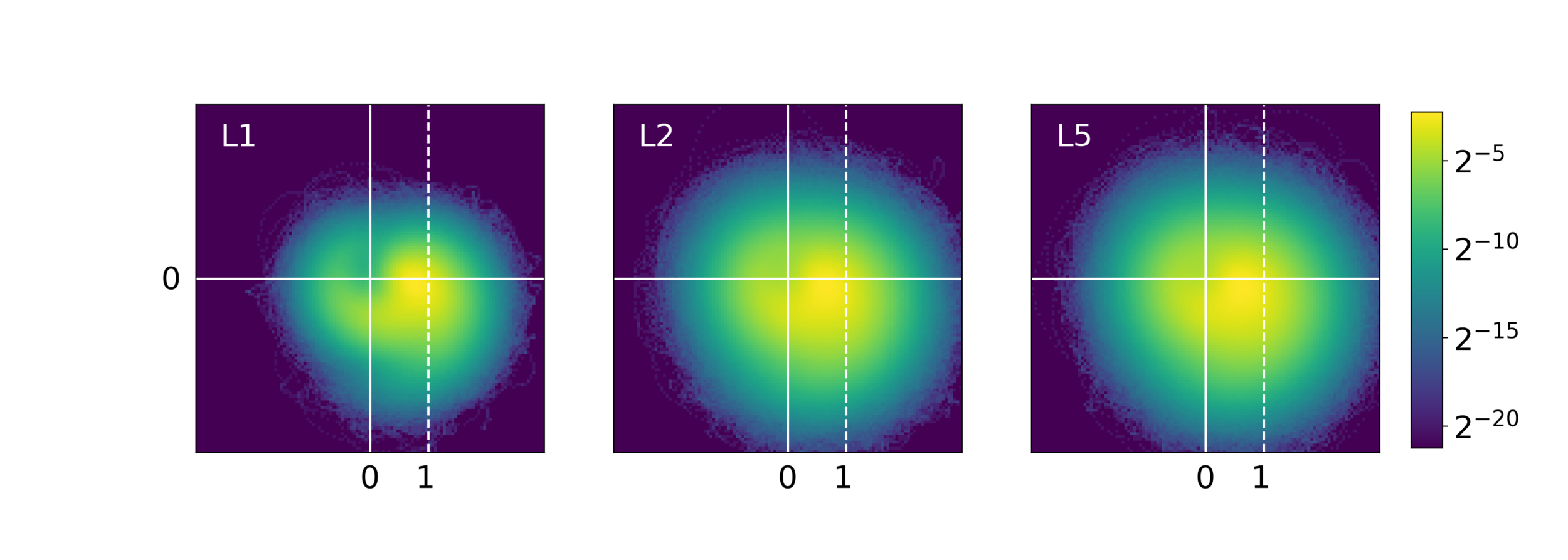
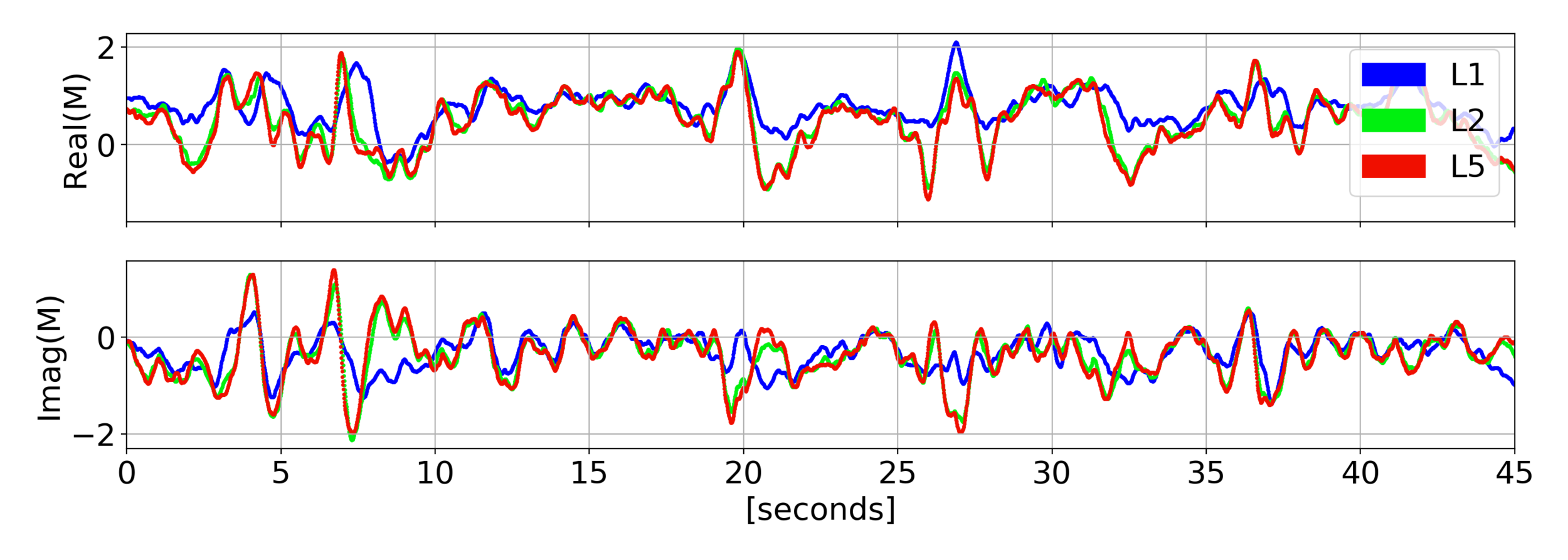
L5

L2

L1

Phase Transitions

Examples

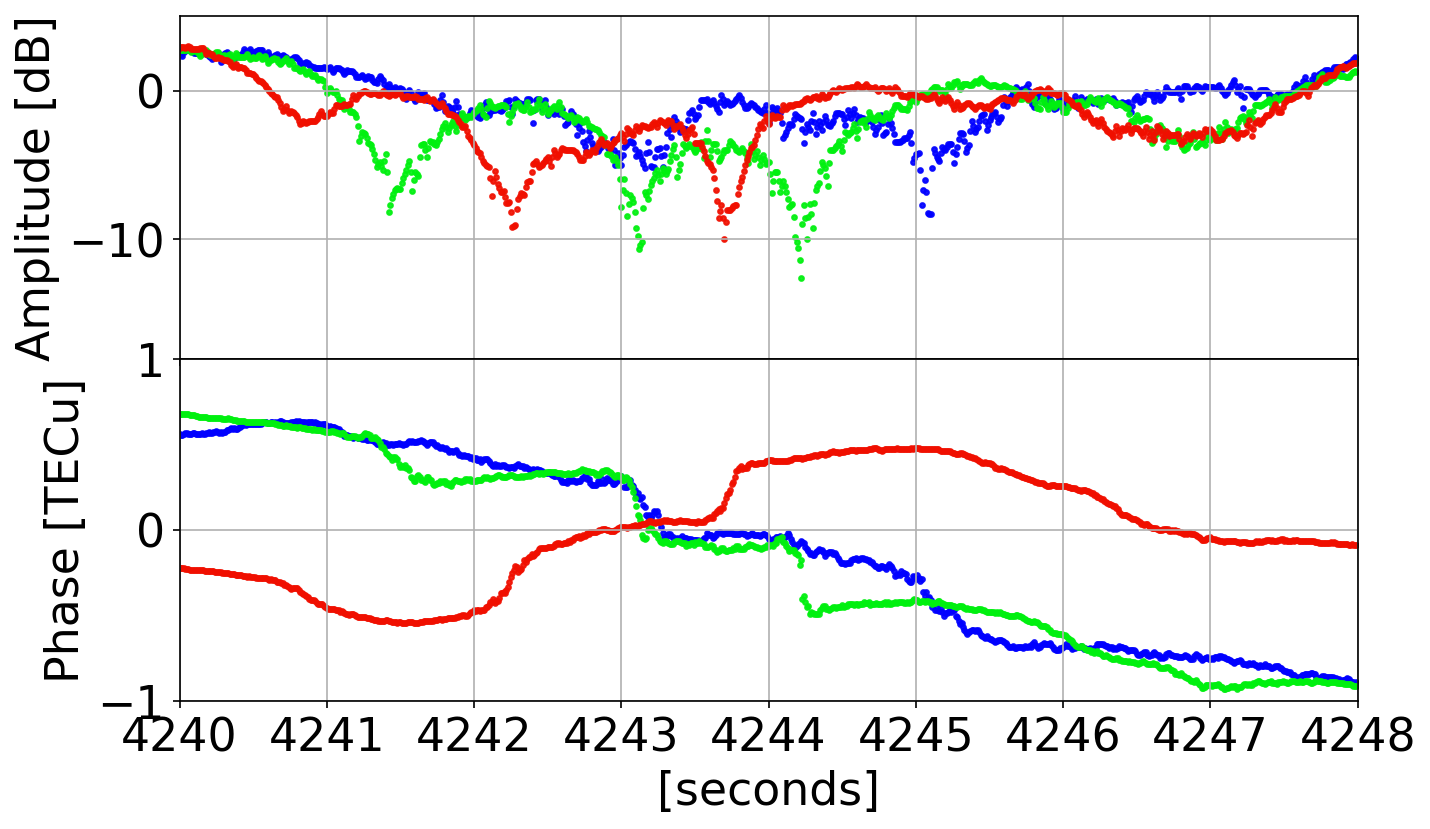
L5

L2

L1

Phase Transitions

Examples

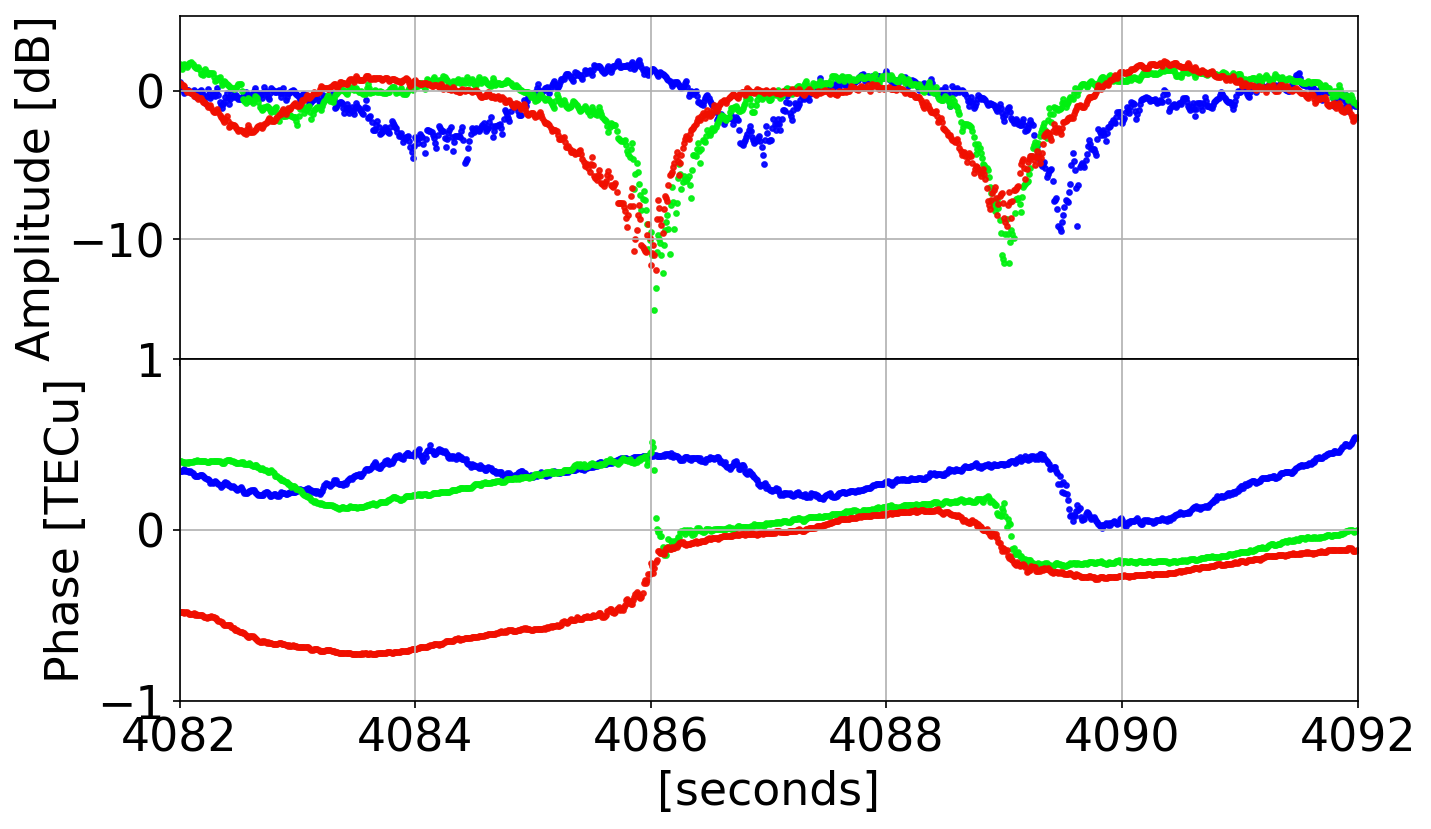
Phase Transitions

Linear Combinations

\frac{\lambda_k}{2\pi} \phi_k= G - \alpha_k T - \frac{\lambda_k}{2\pi}\tilde{\phi}_k

Ionosphere-Free (IF)

phase transitions cause correlated errors in state \(G\) and \(T\) estimates

Geometry-Free (GF)

difficult to discriminate state and multipath dynamics

Cycle Slips    vs     Phase Transitions

  • caused by propagation environment (multipath)
  • not instantaneous
  • usually an artifact of receiver processing
  • instantaneous

Addressing phase transitions in semi-coherent signals requires a special approach that incorporates high-rate signal phase and amplitude measurements along with along with robust models of random multipath

generally easier to correct

difficult to even see

Motivation: Semi-Coherent Examples

Problem: Phase Transitions

Solution: (Particle Filter Algorithm)

Background: Signal Model

Why Particle Filter?

  • Bayesian, multi-modal
  • sequential
  • good at dealing with non-linearity
M_k = \tilde{A}_k\exp(i\tilde{\phi}_k)

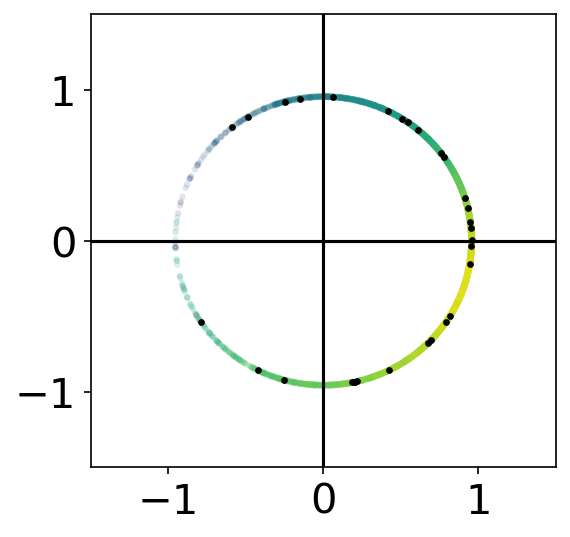
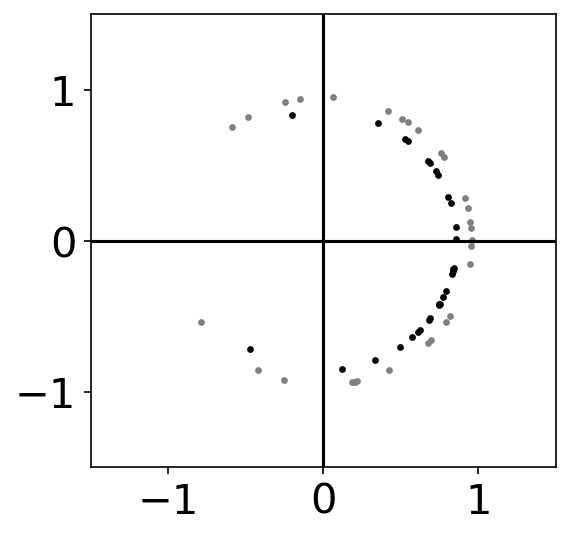
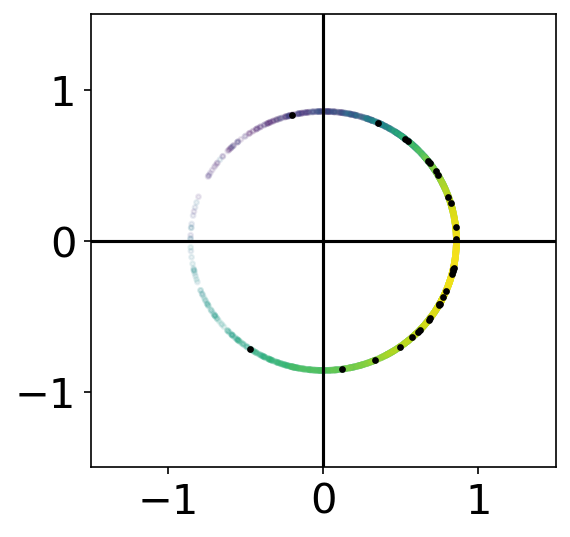
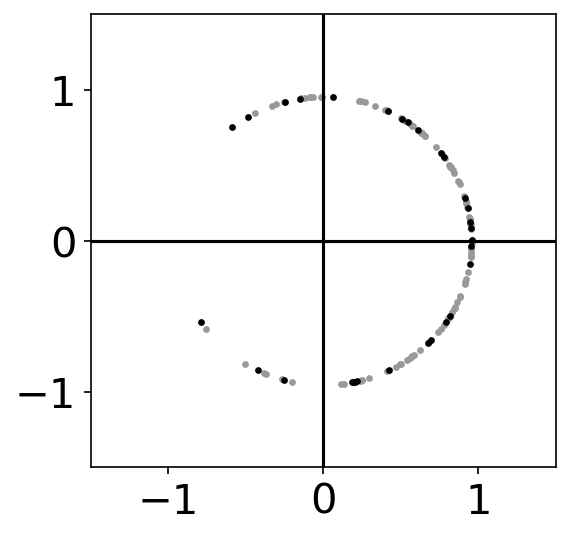
Sample \(N_p\) states from \(q_1(\mathbf{x}_{1})\)

Compute weights \(w(\mathbf{x}_{1:n}) \propto p(\mathbf{M}) \)

\(\mathbf{M}_n\)

Propagate to time \(n+1\)

Resample from \(q_{n}(\mathbf{x}_{1:n})\)

\(w(\mathbf{x}_n)\)

Particle Filter Details

Posterior Target Distribution

Ideal Measurement Assumption

Initial Proposal Distribution

q_1(\mathbf{x}_{1}) \propto \mathcal{N}(G_1; \mu_{G_1}, 0.05) \mathcal{N}(T_1; \mu_{T_1}, 0.1) \delta(\mathbf{y}_1 - H\mathbf{x}_1)
p(\mathbf{x}_{1:n} | \mathbf{y}_{1:n}) \propto p(\mathbf{y}_{1:n} | \mathbf{x}_{1:n})p(\mathbf{x}_{1:n})

Subsequent Proposal Distribution

q_n(\mathbf{x}_{1:n}) \propto \mathcal{N}(G_n; G_{n-1}, \sigma_{G_n}^2)\mathcal{N}(T_n; T_{n-1}, \sigma_{T_n}^2) \delta(\mathbf{y}_n - H\mathbf{x}_n)
p(\mathbf{y}_{1:n} | \mathbf{x}_{1:n}) = \delta(\mathbf{y}_{1:n} - H\mathbf{x}_{1:n})
  • reduces problem dimensionality
  • measurement noise can be partially absorbed into \(\mathbf{M}\) model

Weights

w(\mathbf{x}_{1:n}) \propto p(\mathbf{M}_n|\mathbf{M}_{n-1})

Other Details

  • systematic resampling
  • 5000 particles

Multipath Dynamics Model

How can we define \(p(\mathbf{M}_{(1:n)})\)?

  • highly-correlated non-linear random process

  • we approximate locally-normal correlated random process with state-dependent covariance
p(\mathbf{M}_n|\mathbf{M}_{n-1})\sim\mathcal{N}(\mathbf{M}_{n-1}, \Sigma(\mathbf{M}_{n-1})) p_0(M_n)
p_0(M_n)

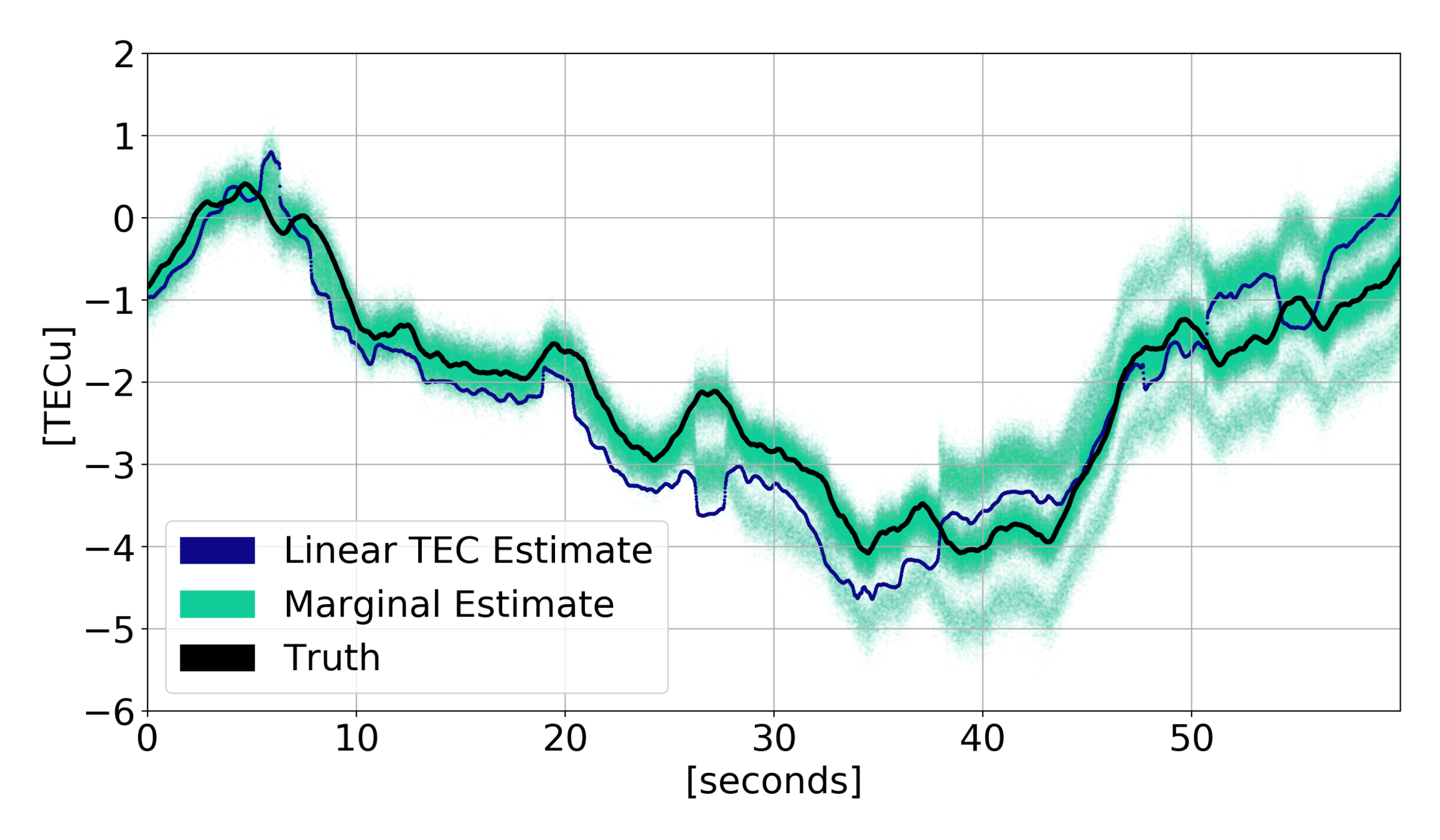
Results...

This was not a resounding success.

But we still can learn a lot.

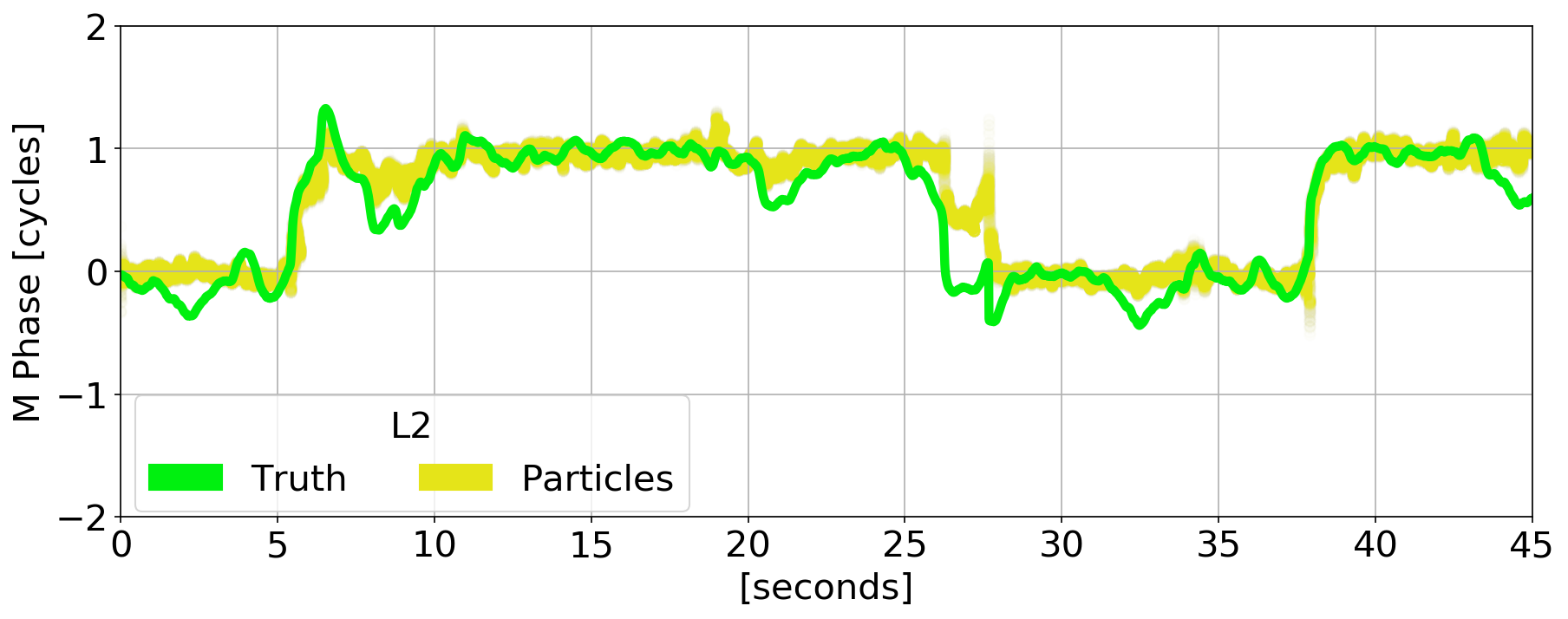
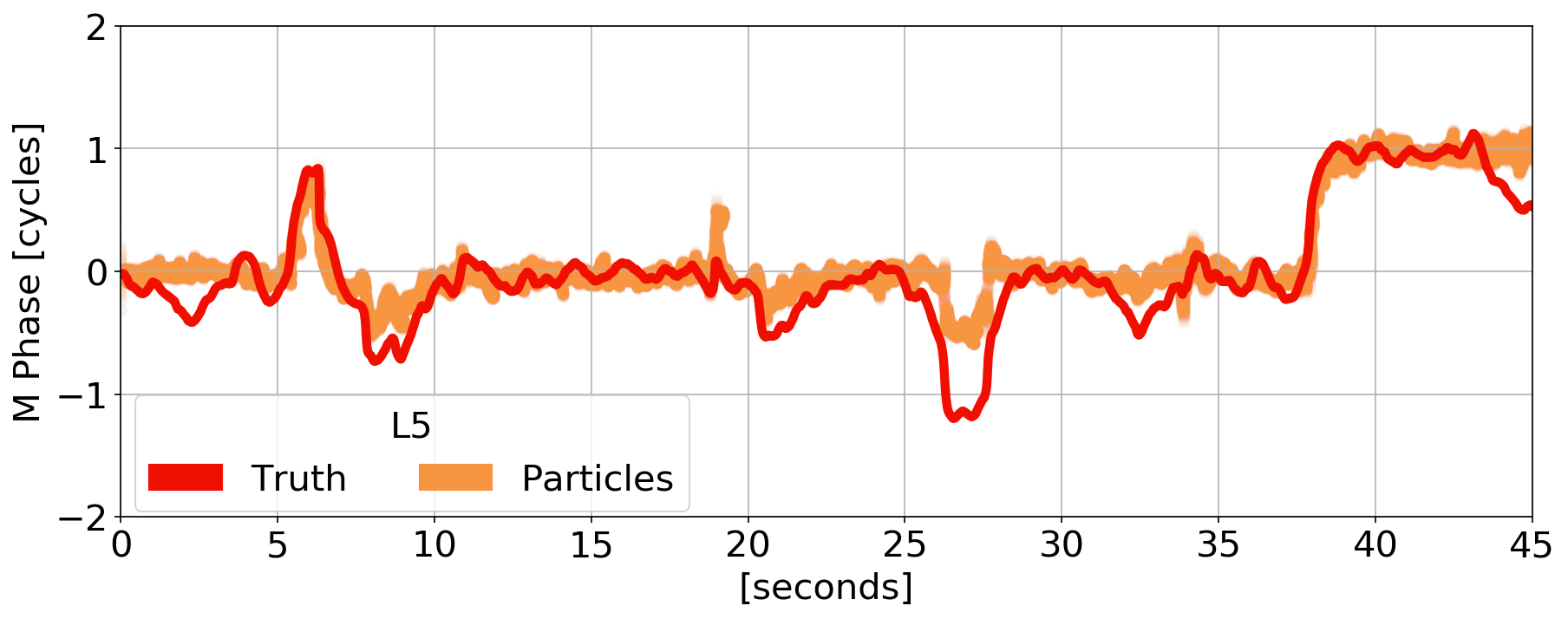
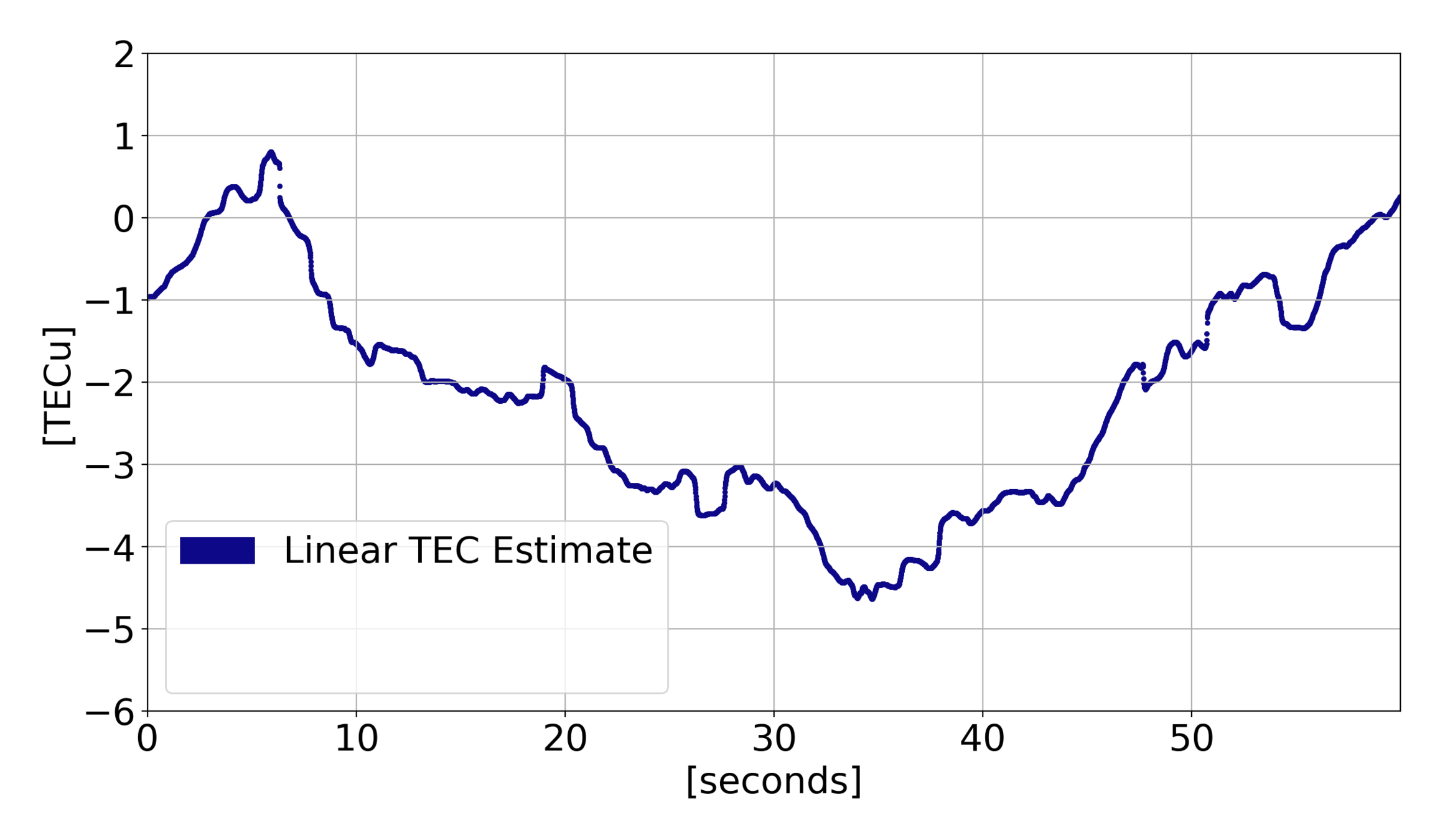
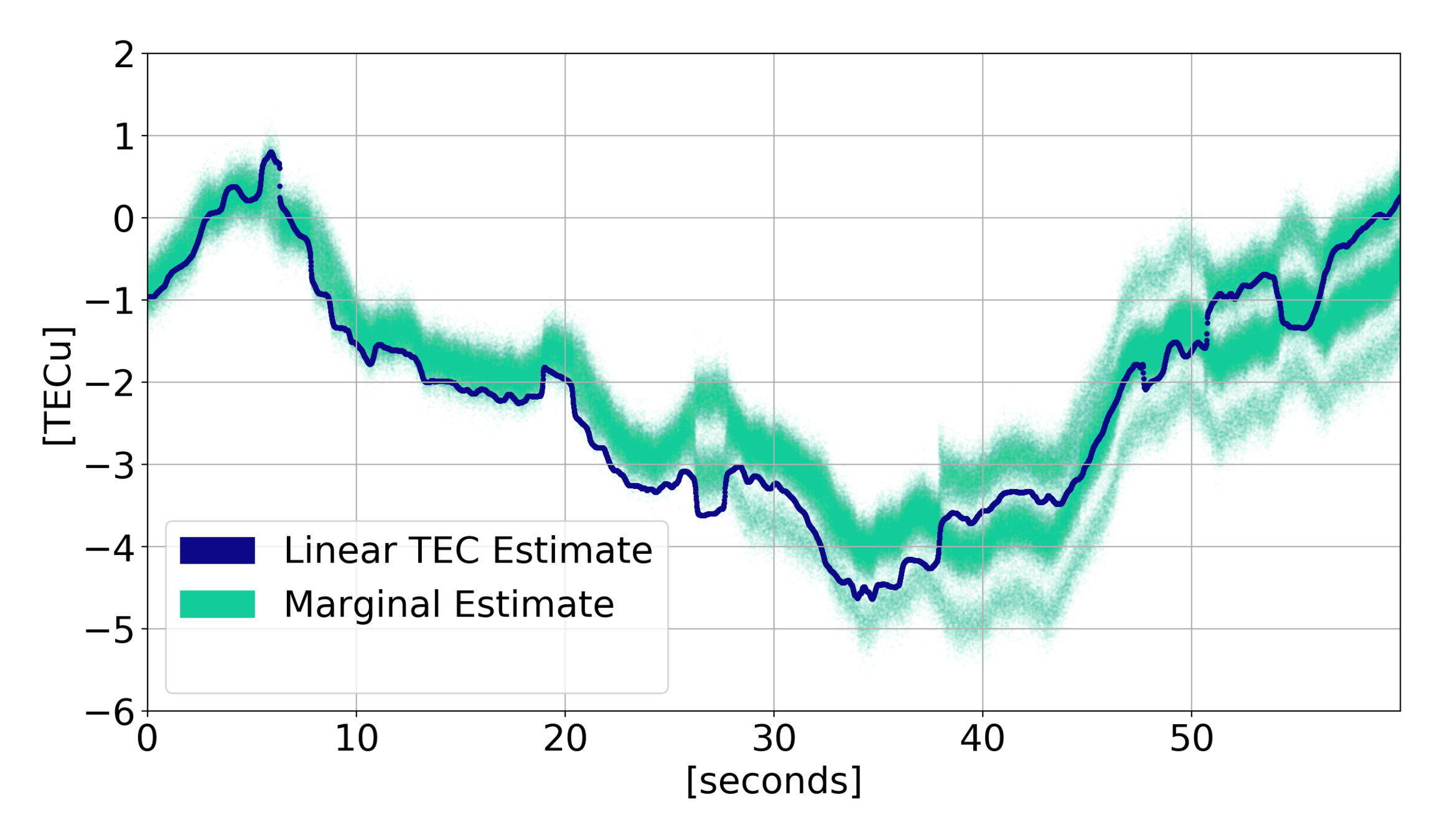
Estimation Results

   \(\tilde{\phi}\) Errors

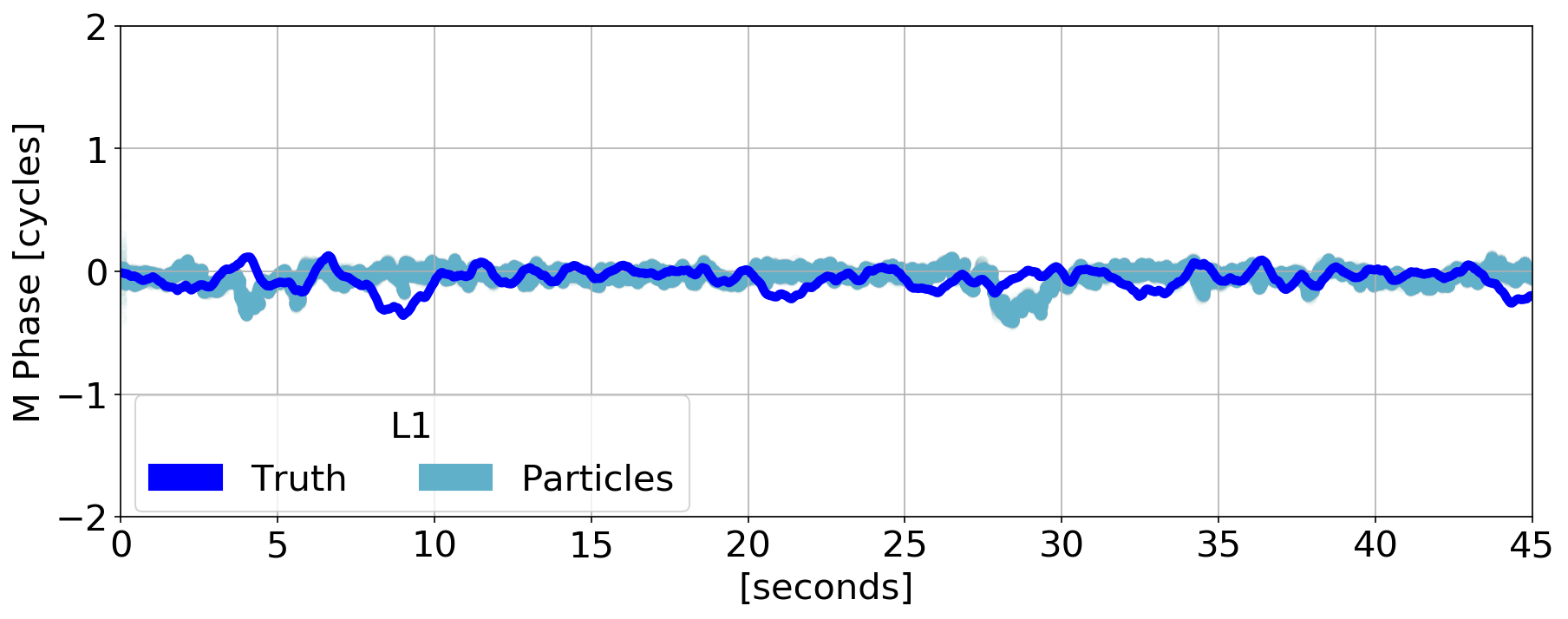
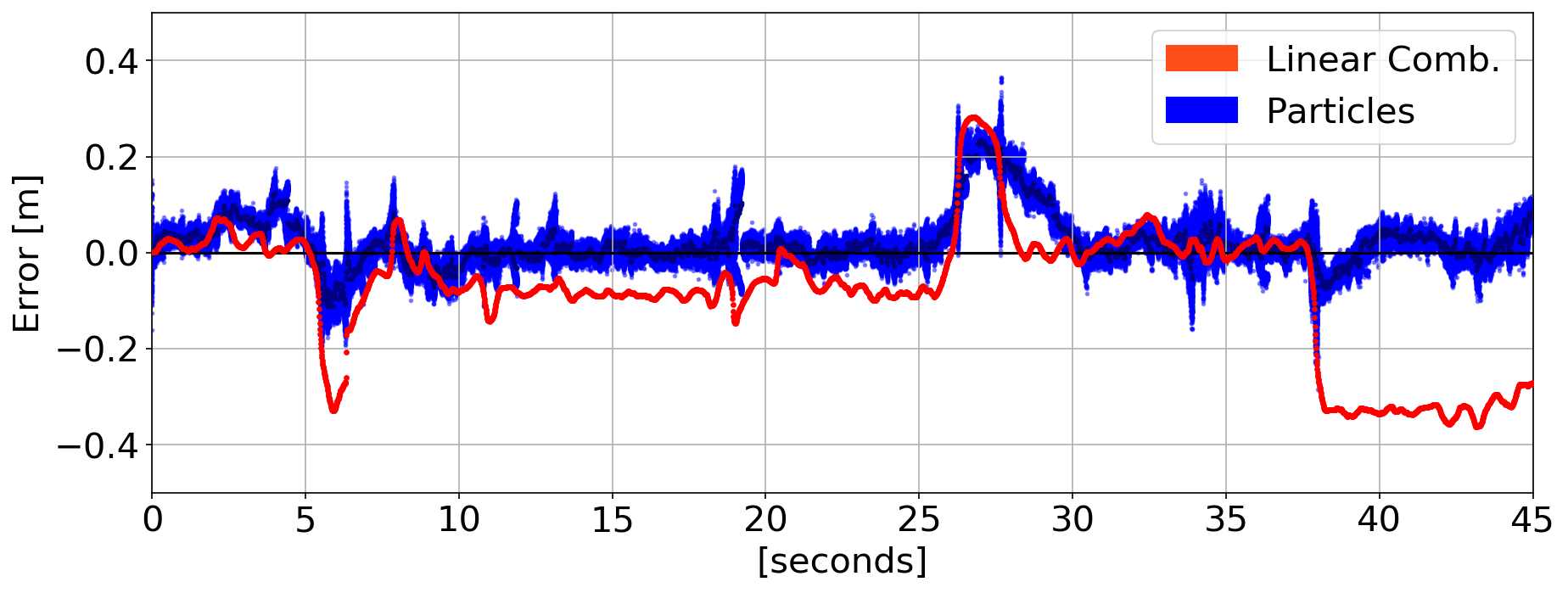
Estimation Results

   \(\tilde{\phi}\) Errors

Estimation Results

   \(G\) and \(T\) Errors

  1. Avoids jumps and biases due to phase transitions
  2. Filters some diffraction fluctuations

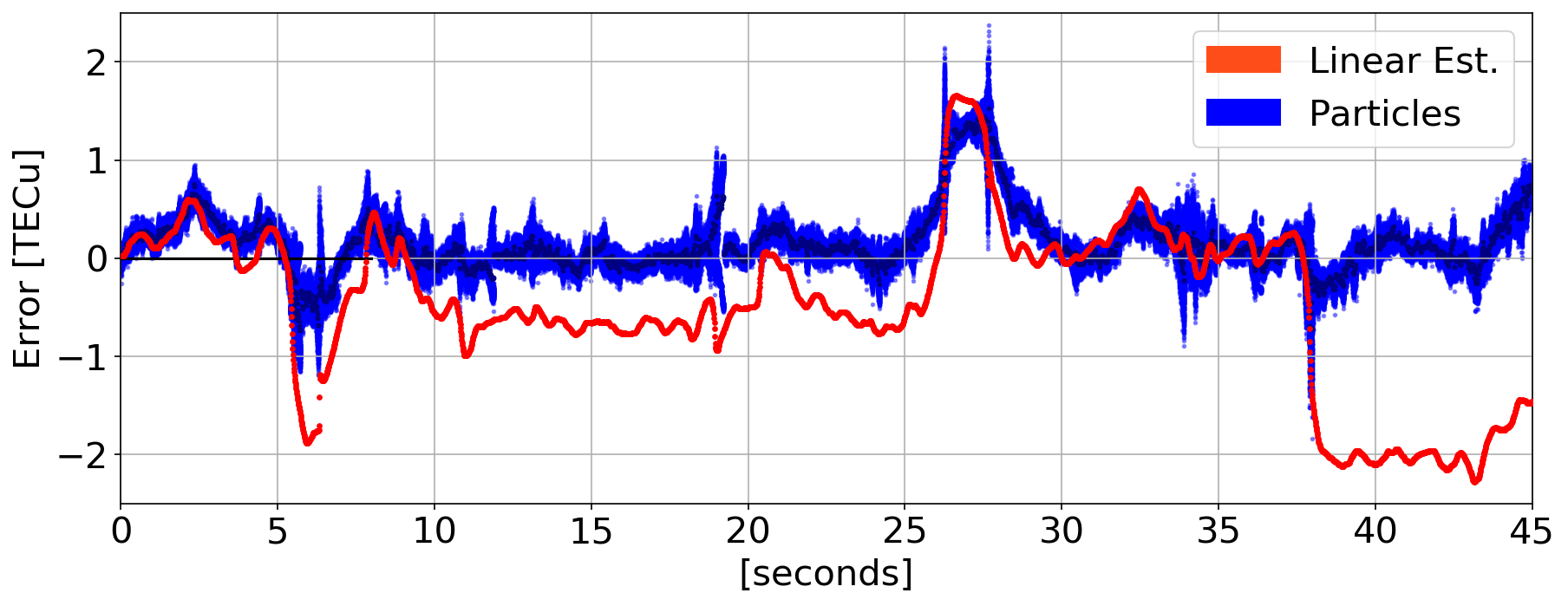
\(G\)

\(T\)

Particle Filter Summary

How well did this work?

The Good

The Bad

  • estimates phase transitions
  • marginal bifurcation
  • reduced errors in \(G\) and \(T\) estimates
  • insufficient spread in state estimate
    • particle filter degeneracy
  • some large dynamics in \(G\) and \(T\)

Key Points

Motivation:

Phase transitions cause large errors in connected phase from semi-coherent signals

Even with multi-frequency information, discriminating state and multipath dynamics is challenging/ambiguous

Particle Filter:

Not sufficient for separating multipath from other state dynamics

Next Steps:

We will try moving-window Bayesian estimation approaches

Acknowledgements

Contact

Brian Breitsch

brianbreitsch@colorado.edu

Spire

Carolyn J Roesler

Rong Yang

Steve Taylor and Harrison Bourne

  • LEO ocean reflectometry data
  • Help with Spire data
  • Help with mountaintop RO data
  • GNSS data collection

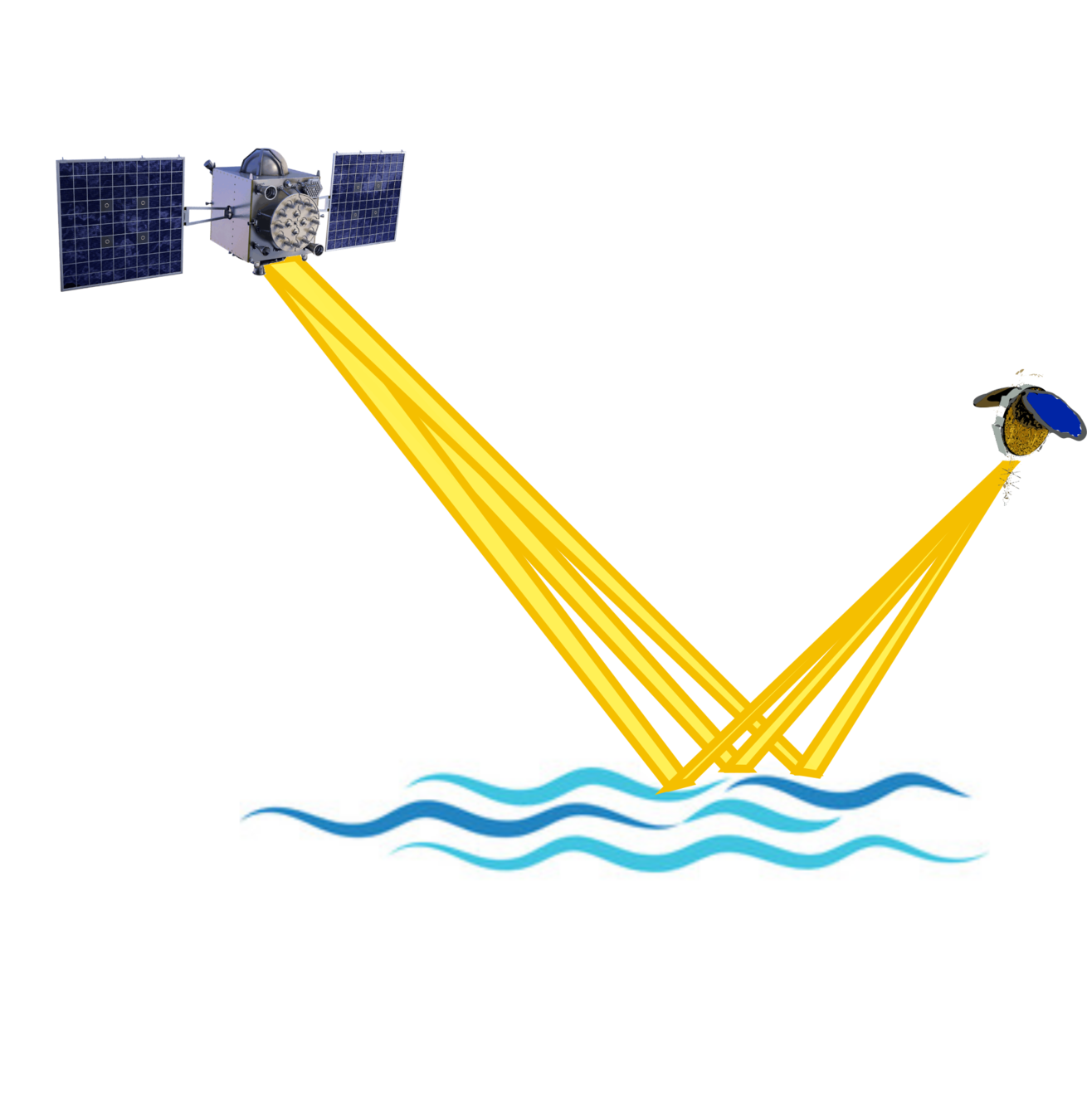
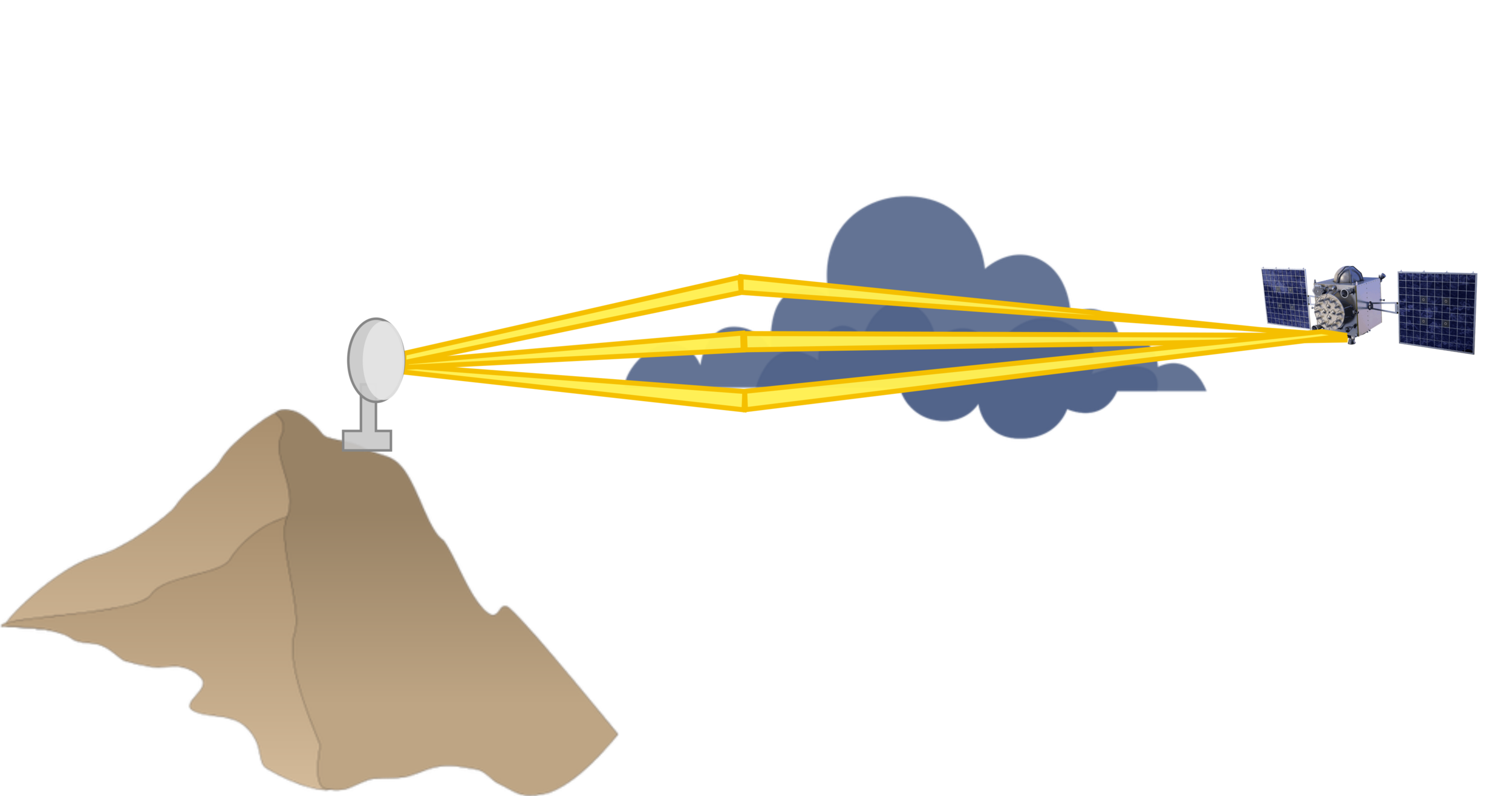
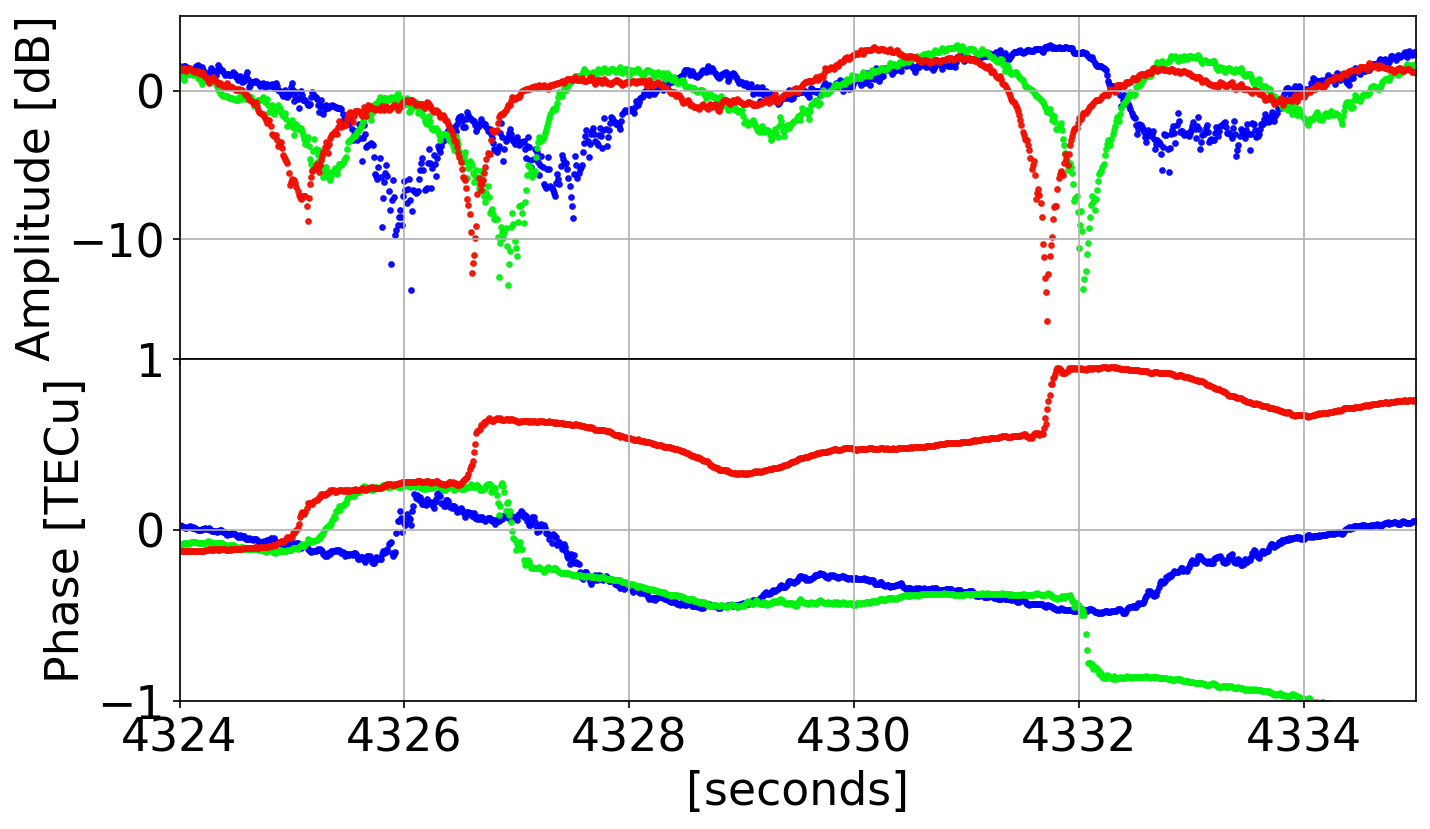
Semi-Coherent Signals:

Ocean Reflection (Spire satellite)

\(\text{reflected} - \text{direct}\)

L5

L2

L1

Phase Transitions

Examples

Why Particle Filter?

  • Bayesian
  • sequential
  • good at dealing with non-linearity
M_k = \tilde{A}_k\exp(i\tilde{\phi}_k)

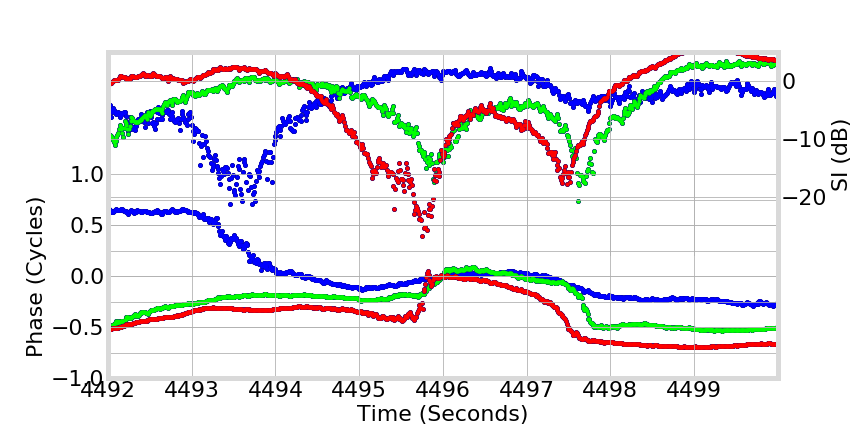
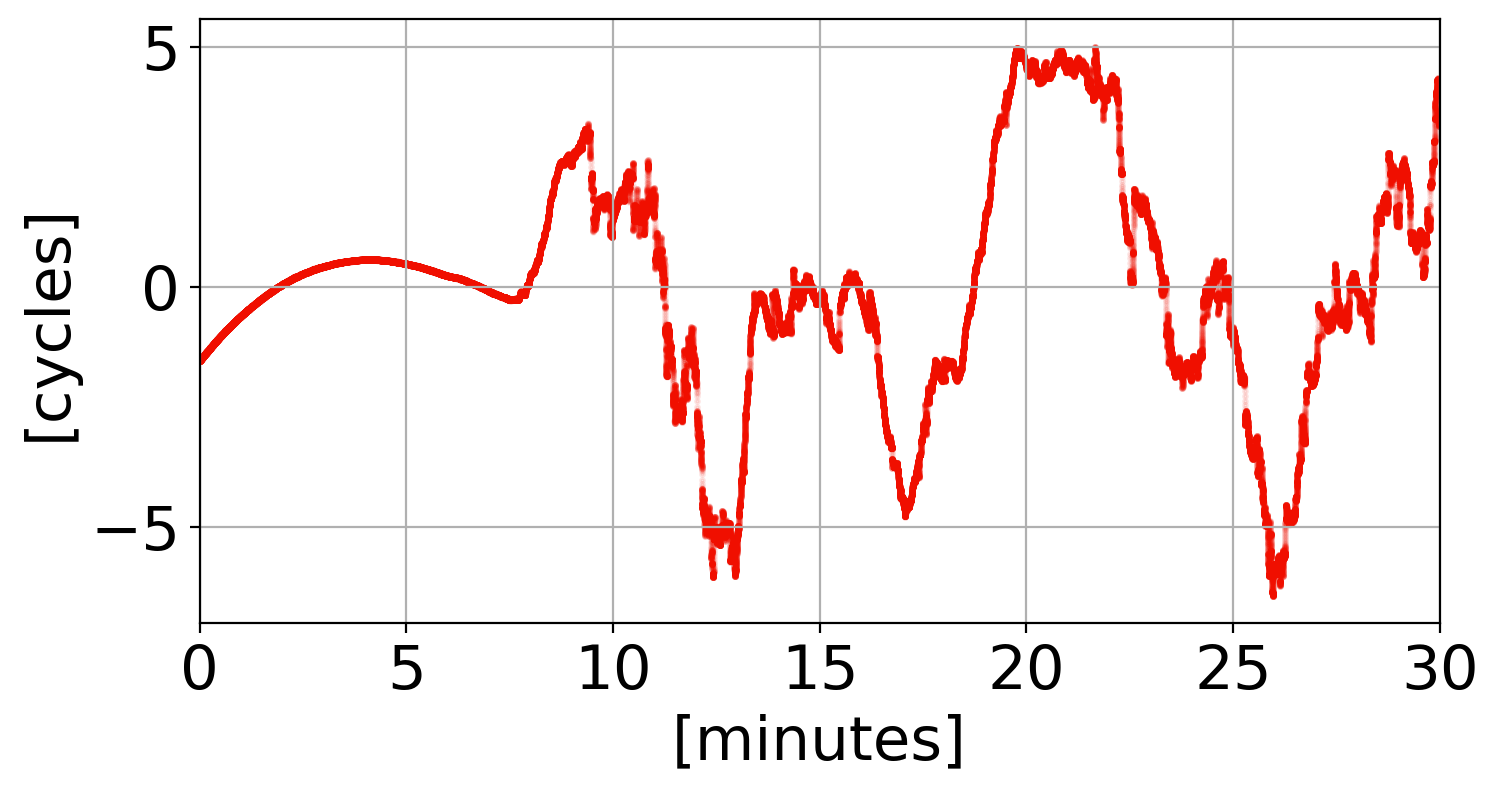
L5

L2

L1

Phase Transitions

Ascension Island

L5

L2

L1

Phase Transitions

Ascension Island

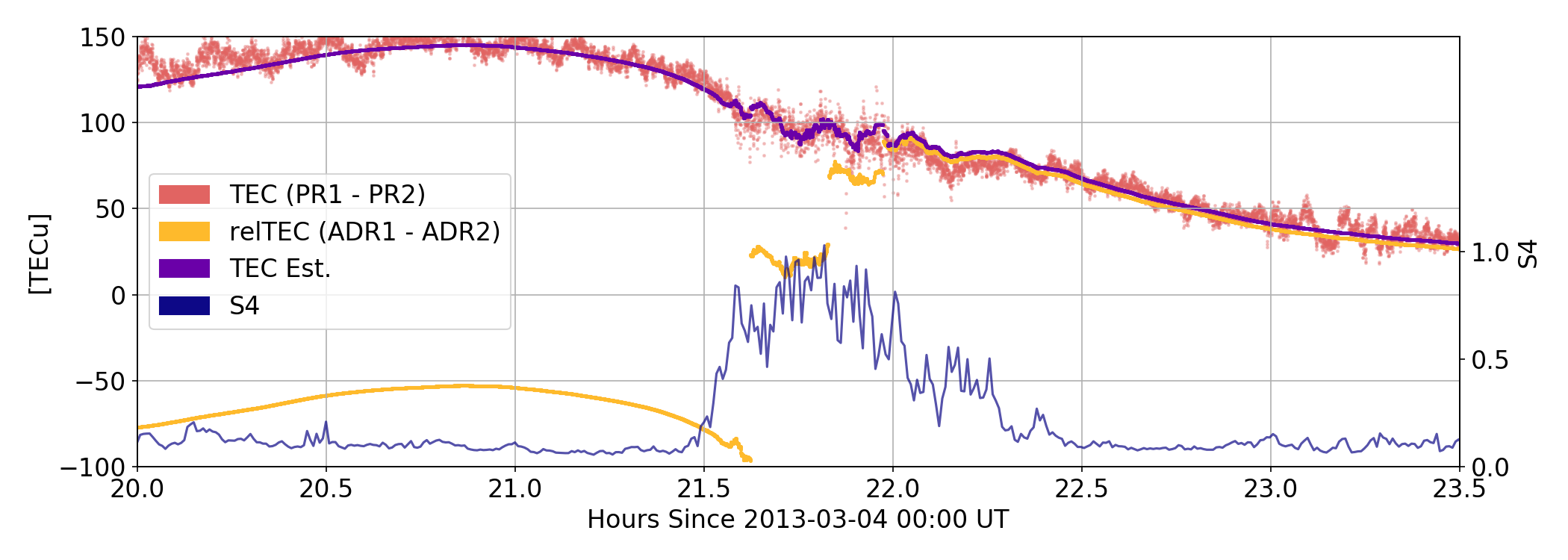
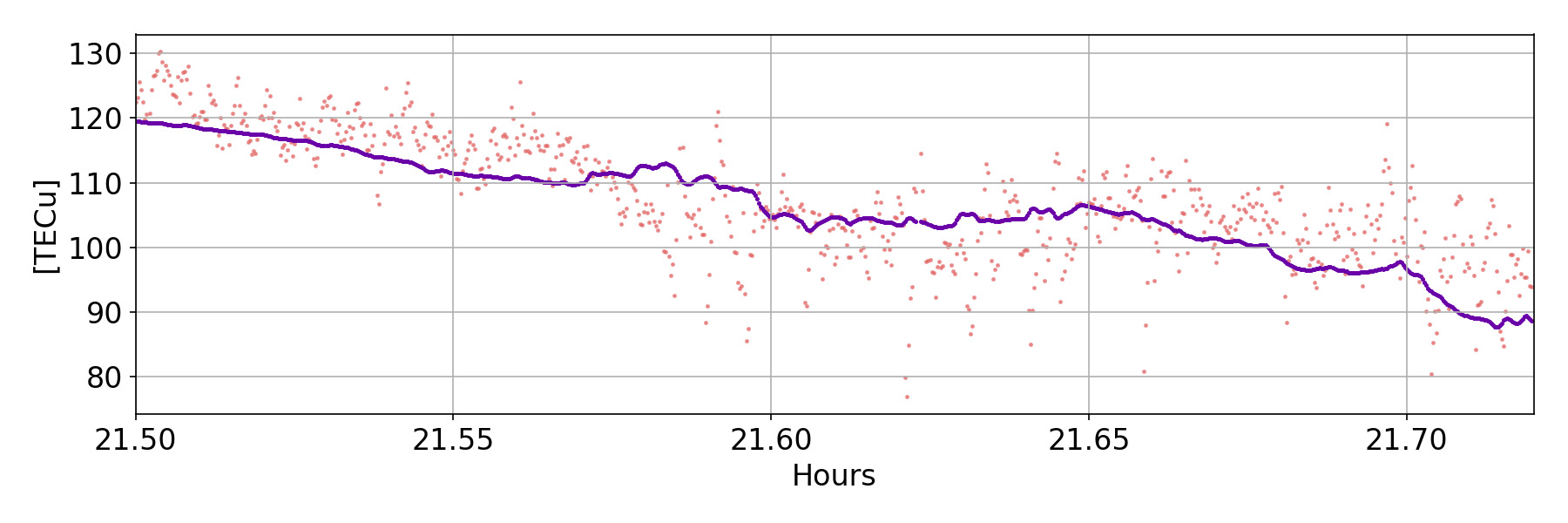
Phase Transitions

Attempted removal in real scintillation data (Hong Kong, Septentrio ground antenna)

phase transitions

Particle Filter Details

Perfect Measurement Assumption

If we assume no phase measurement noise, then:

p(\mathbf{y}|\mathbf{x}) = \delta(\mathbf{y}_\Phi - H_\Phi\mathbf{x}) p(\mathbf{y}_A | \mathbf{x}_A)

and

p(\mathbf{x}|\mathbf{y}) = \frac{\delta(\mathbf{y} - H\mathbf{x}) p(\mathbf{x})}{p(\mathbf{y})}

i.e. find the most likely state sequence that satisfies our measurements.

prior probability of state sequence

this is the hard part

not straightforward