Electron Density Reconstruction in the Ionosphere

Brian Breitsch

Advisor: Dr. Jade Morton

TEC, tomography, assimilation, GNSS occultations, spherical symmetry

A vague, uninformed, and somewhat rambling overview of

Outline

  • TEC
  • tomography
  • ionosonde/ISR
  • radio occultation
  • spherical symmetry inversion
    • derivation
    • results
    • limitations
  • other imaging methods using RO

Electron Density 

and Reconstruction

  • electron density        is the image

 

  • total electron content               is the typical observable
    • also                ,                ,               

 

  •              is the path integral of
N_e
NeN_e
TEC
TECTEC
TEC
TECTEC
N_e
NeN_e
VTEC
VTECVTEC
STEC
STECSTEC
LTEC
LTECLTEC

Austen et. al. 1988

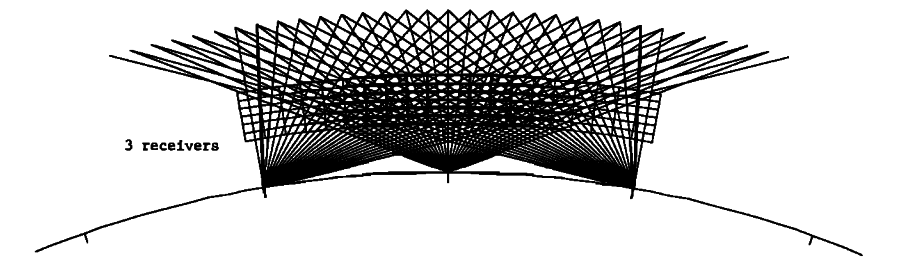
three receiver simulation geometry

Ionospheric Imaging Using Computerized Tomography

  • simulation study
  • 2D plane
  • suggests feasibility of ionosphere tomography
  • indicates poor vertical resolution

Yeh and Raymund 1991

Limitations of Ionospheric Imaging by Tomography

  • detailed mathematical analysis
  • impulse response methods
  • quantitative results for resolution
    • affirms poor vertical resolution

 

Tomography Successes

  • early success with polar orbiting beacons
  • NNSS (Navy Navigation Satellite System)
    • near-polar orbit at 1000km 

Na et. al. 1990 imaging of ionosphere trough

Tomography Successes

  • Yizengraw et. al. 2003

  • Tomographic reconstruction of the ionosphere using ground-based GPS data in the Australian region

  • GPS satellites in 2D geometry

  • showed ionospheric trough during geomagnetic storm

Tomography Successes

  • many others
  • most using a priori information
    • model-based background
  • many using regularization contraints
    • orthonormal basis functions
      • spherical harmonics
      •  
    • model-based functions
      • Chapman
      • DGR (Giovanni and Radiacella, Radiacella & Zhang 1995)

tomographic image and EISCAT verification, Mitchel et. al. 1997

Problems

  • 2D plane assumption invalid
  • poor vertical resolution
  • poor temporal resolution with GPS satellites
  • ill-posed inverse problem
    • especially in 3D
    • need for regularization
    • need for more data

Ionosondes and ISRs

advantages

  • provide high-resolution vertical information
  • on-demand (ish) sounding

disadvantages

  • size
  • cost to build/operate
  • restricted location
  • bottomside profile only for ionosondes

Radio Occultations

  • Earth limb sounding of TEC (LTEC)
  • provide information with good vertical resolution
  • even, global distribution of soundings
  • useful for tomography                 and model assimilation
  • complementary to ground-GNSS geometry

Reconstruction

radio occultation data can stand on its own

  • spherical symmetry assumption for        provides sufficient regularization
  • resulting inverse problem is well-defined

 

 

  • solution to Abel inversion is least-squares solution to corresponding system
N_e
NeN_e
y = Ax
y=Axy = Ax
A
AA

upper triangular

Reconstruction

assuming spherical symmetry

dx = \frac{r}{\sqrt{r^2 - y^2}} dr
dx=rr2−y2drdx = \frac{r}{\sqrt{r^2 - y^2}} dr
r = \sqrt{y^2 + x^2}
r=y2+x2r = \sqrt{y^2 + x^2}
F(y) = \int_{-\infty}^{\infty}\frac{rf(r)}{\sqrt{r^2 - y^2}} dr
F(y)=∫−∞∞rf(r)r2−y2drF(y) = \int_{-\infty}^{\infty}\frac{rf(r)}{\sqrt{r^2 - y^2}} dr

Reconstruction

layers

  • assume         varies linearly between layers
N_e
NeN_e
N_i(r) = N(p_{i-1}) + \frac{N(p_{i}) - N(p_{i-1})}{p_{i} - p_{i-1}} (r - p_{i-1})
Ni(r)=N(pi−1)+N(pi)−N(pi−1)pi−pi−1(r−pi−1)N_i(r) = N(p_{i-1}) + \frac{N(p_{i}) - N(p_{i-1})}{p_{i} - p_{i-1}} (r - p_{i-1})

between                  and                   layers, define election density:

i^{th}
ithi^{th}
i-1^{th}
i−1thi-1^{th}
\Rightarrow N_{i}(r) = a_{i} + b_{i} r
⇒Ni(r)=ai+bir\Rightarrow N_{i}(r) = a_{i} + b_{i} r

Reconstruction

TEC observation expression

  • TEC typically defined in TECU:
  • redefine as:
1e16 \text{ electrons} / m^2
1e16 electrons/m21e16 \text{ electrons} / m^2
T(p_i) = 1e16 \cdot TEC(p_i)
T(pi)=1e16⋅TEC(pi)T(p_i) = 1e16 \cdot TEC(p_i)
p_i
pip_i

where       is the impact parameter for layer

i
ii
i = M - 1, ..., 0
i=M−1,...,0i = M - 1, ..., 0
M = \text{ number of layers}
M= number of layersM = \text{ number of layers}
T(p_i) = \sum_{k=1}^m 2 \int_{p_{i+k-1}}^{p_{i+k}} \frac{rN_{i+k}(r)}{\sqrt{r^2 - p_i^2}}dr
T(pi)=∑k=1m2∫pi+k−1pi+krNi+k(r)r2−pi2drT(p_i) = \sum_{k=1}^m 2 \int_{p_{i+k-1}}^{p_{i+k}} \frac{rN_{i+k}(r)}{\sqrt{r^2 - p_i^2}}dr
m = M - i
m=M−im = M - i

Reconstruction

solving integrals

  • plug in linear expression:
  • solve integrals
N_{i}(r) = a_i + b_i r
Ni(r)=ai+birN_{i}(r) = a_i + b_i r
\int_{p_{i+k-1}}^{p_{i+k}} \frac{rN_{i+k}(r)}{\sqrt{r^2 - p_i^2}}dr
∫pi+k−1pi+krNi+k(r)r2−pi2dr\int_{p_{i+k-1}}^{p_{i+k}} \frac{rN_{i+k}(r)}{\sqrt{r^2 - p_i^2}}dr
\int \frac{r}{\sqrt{r^2 - p^2}}dr \Rightarrow \sqrt{r^2 - p^2}
∫rr2−p2dr⇒r2−p2\int \frac{r}{\sqrt{r^2 - p^2}}dr \Rightarrow \sqrt{r^2 - p^2}
\int \frac{r^2}{\sqrt{r^2 - p^2}}dr \Rightarrow \frac{1}{2} \left[ r\sqrt{r^2 - p^2} + p^2 \ln\left|\frac{1}{p}\left(r + \sqrt{r^2 - p^2} \right)\right| \right]
∫r2r2−p2dr⇒12[rr2−p2+p2ln∣1p(r+r2−p2)∣]\int \frac{r^2}{\sqrt{r^2 - p^2}}dr \Rightarrow \frac{1}{2} \left[ r\sqrt{r^2 - p^2} + p^2 \ln\left|\frac{1}{p}\left(r + \sqrt{r^2 - p^2} \right)\right| \right]

Reconstruction

expand solution

\int_{p_{i+k-1}}^{p_{i+k}} \frac{rN_{i+k}(r)}{\sqrt{r^2 - p_i^2}}dr
∫pi+k−1pi+krNi+k(r)r2−pi2dr\int_{p_{i+k-1}}^{p_{i+k}} \frac{rN_{i+k}(r)}{\sqrt{r^2 - p_i^2}}dr
\rho_{i,k} = \frac{ \alpha_{i,k} - \alpha_{i,k-1} }{p_{i+k} - p_{i+k-1}}
ρi,k=αi,k−αi,k−1pi+k−pi+k−1\rho_{i,k} = \frac{ \alpha_{i,k} - \alpha_{i,k-1} }{p_{i+k} - p_{i+k-1}}
\sigma_{i,k} = \frac{ p_{i+k} \alpha_{i,k} - p_{i+k-1} \alpha_{i,k-1} }{2 p_i \left(p_{i+k} - p_{i+k-1}\right)} + \frac{p_i^2}{2\left(p_{i+k} - p_{i+k-1}\right)} \ln \left| \frac{ p_{i+k} + \alpha_{i,k} }{ p_{i+k-1} + \alpha_{i,k-1} } \right|
σi,k=pi+kαi,k−pi+k−1αi,k−12pi(pi+k−pi+k−1)+pi22(pi+k−pi+k−1)ln∣pi+k+αi,kpi+k−1+αi,k−1∣\sigma_{i,k} = \frac{ p_{i+k} \alpha_{i,k} - p_{i+k-1} \alpha_{i,k-1} }{2 p_i \left(p_{i+k} - p_{i+k-1}\right)} + \frac{p_i^2}{2\left(p_{i+k} - p_{i+k-1}\right)} \ln \left| \frac{ p_{i+k} + \alpha_{i,k} }{ p_{i+k-1} + \alpha_{i,k-1} } \right|
  • define:
2\sum_{k=1}^m \left[ N(p_{i+k-1}) \left( p_{i+k} \rho_{i,k} - \sigma_{i,k} \right) - N(p_{i+k}) \left( p_{i+k-1} \rho_{i,k} - \sigma_{i,k} \right) \right]
2∑k=1m[N(pi+k−1)(pi+kρi,k−σi,k)−N(pi+k)(pi+k−1ρi,k−σi,k)]2\sum_{k=1}^m \left[ N(p_{i+k-1}) \left( p_{i+k} \rho_{i,k} - \sigma_{i,k} \right) - N(p_{i+k}) \left( p_{i+k-1} \rho_{i,k} - \sigma_{i,k} \right) \right]
T(p_i) =
T(pi)=T(p_i) =
\alpha_{i,k} = \sqrt{p_{i+k}^2 - p_{i}^2}
αi,k=pi+k2−pi2\alpha_{i,k} = \sqrt{p_{i+k}^2 - p_{i}^2}

Reconstruction

group corresponding layers

\frac{T(p_i)}{2} =
T(pi)2=\frac{T(p_i)}{2} =
N(p_i) (p_{i+1} \rho_{i,1} - \sigma_{i,1})
N(pi)(pi+1ρi,1−σi,1) N(p_i) (p_{i+1} \rho_{i,1} - \sigma_{i,1})
+ \sum_{k=1}^{m-1} N(p_{i+k}) \left( p_{i+k+1} \rho_{i, k+1} - \sigma_{i, k+1} - p_{i+k-1} \rho_{i, k} + \sigma_{i, k} \right)
+∑k=1m−1N(pi+k)(pi+k+1ρi,k+1−σi,k+1−pi+k−1ρi,k+σi,k) + \sum_{k=1}^{m-1} N(p_{i+k}) \left( p_{i+k+1} \rho_{i, k+1} - \sigma_{i, k+1} - p_{i+k-1} \rho_{i, k} + \sigma_{i, k} \right)
- N(p_{i+m})(p_{i+m-1} \rho_{i,m} - \sigma_{i,m})
−N(pi+m)(pi+m−1ρi,m−σi,m) - N(p_{i+m})(p_{i+m-1} \rho_{i,m} - \sigma_{i,m})

Reconstruction

final expression

N(p_i) = \frac{1}{p_{i+1}\rho_{i,1} - \sigma_{i,1}} \left[ \frac{T(p_i)}{2} \right]
N(pi)=1pi+1ρi,1−σi,1[T(pi)2]N(p_i) = \frac{1}{p_{i+1}\rho_{i,1} - \sigma_{i,1}} \left[ \frac{T(p_i)}{2} \right]
- \sum_{k=1}^{m-1} N(p_{i+k}) \left( p_{i+k+1} \rho_{i, k+1} - \sigma_{i, k+1} - p_{i+k-1} \rho_{i, k} + \sigma_{i, k} \right)
−∑k=1m−1N(pi+k)(pi+k+1ρi,k+1−σi,k+1−pi+k−1ρi,k+σi,k)- \sum_{k=1}^{m-1} N(p_{i+k}) \left( p_{i+k+1} \rho_{i, k+1} - \sigma_{i, k+1} - p_{i+k-1} \rho_{i, k} + \sigma_{i, k} \right)
\left[ + N(p_{i+m})(p_{i+m-1} \rho_{i,m} - \sigma_{i,m}) \right]
[+N(pi+m)(pi+m−1ρi,m−σi,m)]\left[ + N(p_{i+m})(p_{i+m-1} \rho_{i,m} - \sigma_{i,m}) \right]

Reconstruction

top-layer density

N(p_i) = N(p_M)
N(pi)=N(pM)N(p_i) = N(p_M)
  • assume             is constant for      near
N(p_i)
N(pi)N(p_i)
p_i
pip_i
p_M
pMp_M

then

T(p) = 2\int_p^{p_M} \frac{r N(p_M)}{\sqrt{r^2 - p^2}} dr = 2 N(p_M) \sqrt{p_M^2 - p^2}
T(p)=2∫ppMrN(pM)r2−p2dr=2N(pM)pM2−p2T(p) = 2\int_p^{p_M} \frac{r N(p_M)}{\sqrt{r^2 - p^2}} dr = 2 N(p_M) \sqrt{p_M^2 - p^2}
= 2 N(p_M) \sqrt{(p_M + p)(p_M - p)}
=2N(pM)(pM+p)(pM−p)= 2 N(p_M) \sqrt{(p_M + p)(p_M - p)}
\approx 2 N(p_M) \sqrt{2 p_M (p_M - p)}
≈2N(pM)2pM(pM−p)\approx 2 N(p_M) \sqrt{2 p_M (p_M - p)}

perform fit of top few       measurements to find

TEC
TECTEC
N(p_M)
N(pM)N(p_M)

Reconstruction

above-LEO

  • subtract off              for positive elevation angle
  • usually
TEC
TECTEC
TEC
TECTEC
\approx 1-3 \ \ TEC
≈1−3  TEC\approx 1-3 \ \ TEC

Results

no calibration

Results

DCB calibration (guess/fit)

Results

above-LEO calibration

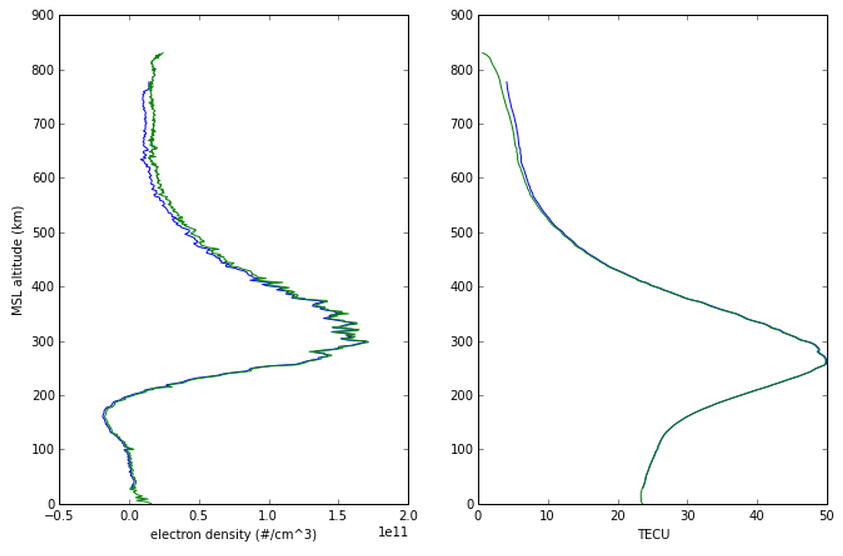
Horizontal Gradients

Case: Ascension Island

  • scintillation amongst GNSS satellites suggests horizontal gradients
  • manifest through invalid electron density profile reconstruction

Horizontal Gradients

impact on spherical symmetry assumption

  • Shaik et. al. 2013 does investigates impact of spherical symmetry assumption in ionospheric imaging
  • found good correlation between horizontal gradients and profile retrieval error

VTEC modeled using NeQuick2 with hypothetical occultation tangent point overlay

Horizontal Gradients

Using VTEC to scale profile shape

<results from paper>

Other Methods

wave-theoretic

  • use LEO orbit as synthetic aperture
  • spectrum inversion
  • addresses multipath concerns
    • not relevant in ionosphere
    • potentially very useful in troposphere

Jensen et. al. 2003 FSI simulation

Model Assimilation

  • includes physics-based a priori model
  • uses all data sources
  • 4D imaging

Simply the most comprehensive and effective way to image the ionosphere.

 

Bust 2008 provides historical context for 2D tomography leading into 4D tomography/assimilation

Tomography/Assimilation

  • Ionospheric Data Assimilation Three Dimensional (IDA3D)
    • uses 3 dimensional variational data assimilation
  • Regional Ionospheric Mapping and Tomography (RIMT)
    • toolkit developed at Cornell, used in multiple studies
  • everyone, everywhere, is/was doing ionosphere imaging
    • Stanford
    • Cornell
    • University of California, Los Angeles
    • University of Texas, Austin
    • University of Calgary, Canada
    • La Trobe University, Bundoora, Australia
    • Wuhan University, China
    • University of Wales, Aberystwyth, U.K.

Data Assimilation

IDA3D

  • Bust et. al. 2007
  • showed convective transport at polar cap

 

Proposal

 

Goal: to improve vertical ionosphere profile reconstruction using RO measurements w/o need for full-blown 3D/4D assimilative model?

  • use IRI for contributions of top-layers in lower-layer reconstruction

 

  • disadvantage: model could have significant bias
  1. Yeh, K. C., and T. D. Raymund. "Limitations of Ionospheric Imaging by Tomography." Wiley Online Library. Radio Science
  2. Radicella, Sandro Maria, and Man-Lian Zhang. "The Improved DGR Analytical Model of Electron Density Height Profile and Total Electron Content in the Ionosphere." Annali Di Geofisica 38 (1995): 35-41.
  3. Montebruck, Oliver, and Eberhard Gill. "Ionospheric Correction for GPS Tracking of LEO Satellites." The Journal of Navigation, n.d. Web. 01 July 2015.
  4. Mitchell, C. N., L. Kersley, J. A. T. Heaton, and S. E. Pryse. "Determination of the Vertical Electron-density Profile in Ionospheric Tomography: Experimental Results." Annales Geophysicae 15 (1997): 747-52.
  5. Hernandez-Pajares, M., J. M. Juan, and J. Sanz. "Improving the Abel Inversion by Adding Ground GPS Data to LEO Radio Occultations in Ionospheric Sounding." Geophysical Research Letters - Wiley Online Library. Group of Astronomy and Geomatics, n.d. Web. 01 July 2015.
  6. Garcia-Fernandez, Miquel, Manuel Hernandez-Pajares, Jose Miguel Juan-Zornoza, and Jaume Sanz-Subirana. "An Improvement of Retrieval Techniques for Ionospheric Radio Occultations." ResearchGate. Astronomy and Geomatics Research Group, n.d. Web. 01 July 2015.
  7. Fremouw, E. J., and James A. Secan. "Application of Stochastic Inverse Theory to Ionospheric Tomography" Radio Science - Wiley Online Library. Radio Science, n.d. Web. 01 July 2015.
  8. Bernhardt, P. A., K. F. Dymond, J. M. Picone, D. M. Cotton, S. Chakrabarti, T. A. Cook, and J. S. Vickers. "Improved Radio Tomography of the Ionosphere Using EUV/optical Measurements from Satellites." Radio Sci. Radio Science 32.5 (1997)
  9. Spencer, Paul S. J., Douglas S. Robertson, and Geral L. Mader. "Ionospheric Data Assimilation Methods for Geodetic Applications." (2005): n. pag. Web.