Improved Estimation of Ionosphere TEC Using Triple-Frequency GPS Signals

Brian Breitsch

Advisor: Dr. Jade Morton

  • Background and Motivation
  • Geometry-free Combinations
  • ILS TEC Estimation
  • Experiment
  • TEC Leveling
    • VTEC Gradient-Mapping Method
  • Results
  • Conclusions / Future Work

Ionosphere TEC

TEC = \int_{\text{rx}}^\text{sat} N_e(x) dx
TEC=∫rxsatNe(x)dxTEC = \int_{\text{rx}}^\text{sat} N_e(x) dx

ionosphere-induced range error for a particular satellite and carrier frequency

\approx \frac{f^2}{40.3\times 10^{16}}I_{S,f}
≈f240.3×1016IS,f\approx \frac{f^2}{40.3\times 10^{16}}I_{S,f}

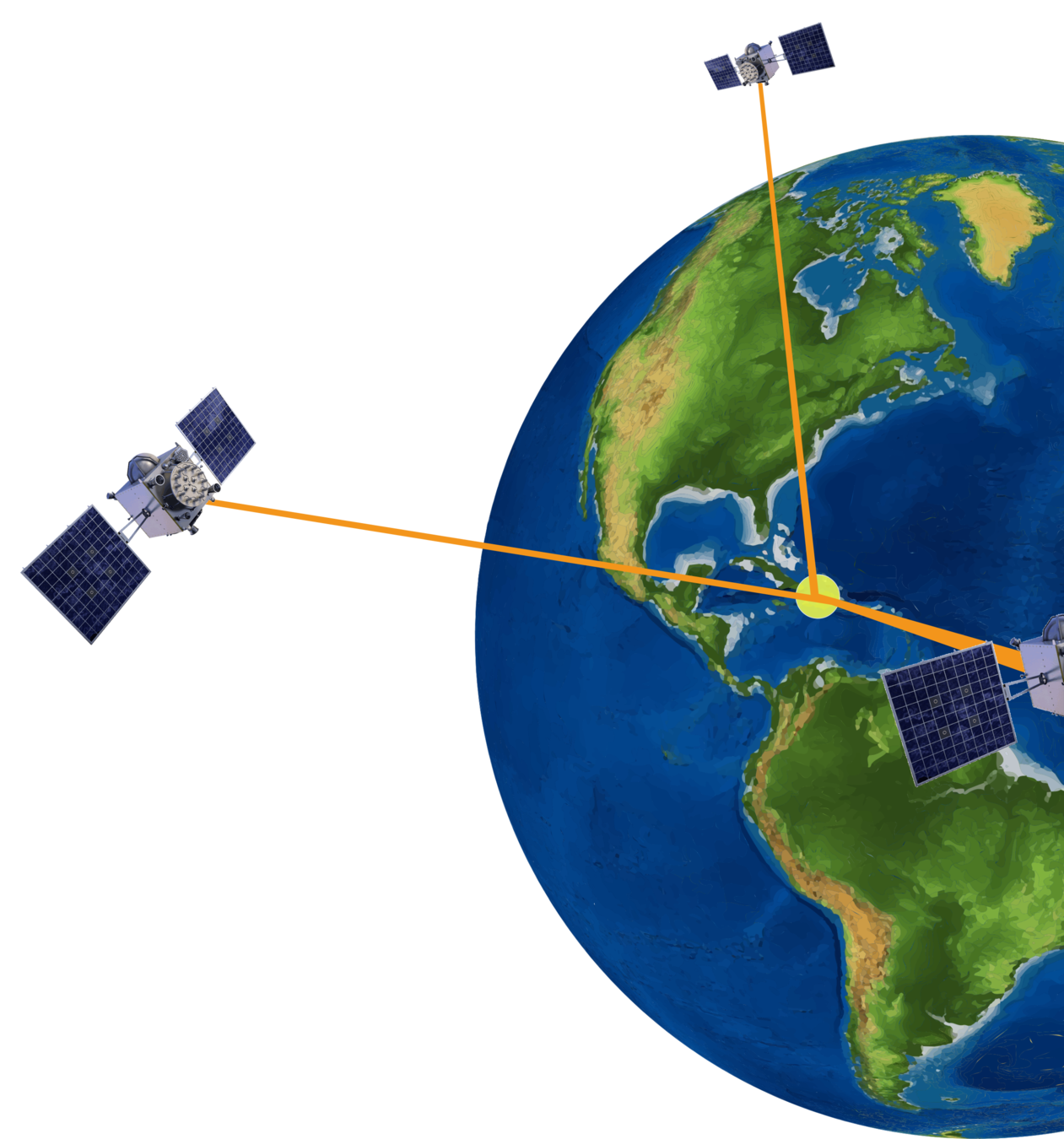
1st-order approx.

GNSS Observations

\rho_{S,f} = r_S + c\left( \Delta t_s - \Delta t_R \right) + T_S
ρS,f=rS+c(Δts−ΔtR)+TS\rho_{S,f} = r_S + c\left( \Delta t_s - \Delta t_R \right) + T_S
+ b^\rho_{S,f} + b^\rho_{R,f} + I_{S,f} + M^\rho_{S,f} + \epsilon^\rho_{S,f}
+bS,fρ+bR,fρ+IS,f+MS,fρ+ϵS,fρ+ b^\rho_{S,f} + b^\rho_{R,f} + I_{S,f} + M^\rho_{S,f} + \epsilon^\rho_{S,f}
\phi_{S,f} = r_S + c\left( \Delta t_s - \Delta t_R \right) + T_s
ϕS,f=rS+c(Δts−ΔtR)+Ts \phi_{S,f} = r_S + c\left( \Delta t_s - \Delta t_R \right) + T_s
+ b^\phi_{S,f} + b^\phi_{R,f} - I_{S,f} + \lambda_f N_{S,f} + M^\phi_{S,f} + \epsilon^\phi_{S,f}
+bS,fϕ+bR,fϕ−IS,f+λfNS,f+MS,fϕ+ϵS,fϕ+ b^\phi_{S,f} + b^\phi_{R,f} - I_{S,f} + \lambda_f N_{S,f} + M^\phi_{S,f} + \epsilon^\phi_{S,f}

HARDWARE

BIAS

IONOSPHERE DELAY

CARRIER

AMBIGUITY

MULTIPATH EFFECTS

FREQUENCY INDEPENDENT EFFECTS

Previous Work

Dissertation by Justine Spitz focused on 3-frequency signal combinations allowing improved real-time resolution of carrier ambiguities and TEC estimation

L1CA

L2C

L5

linear combination

loss of information

TEC \approx \frac{\alpha_{f_i, f_j}}{40.3\times 10^{16}} \left( I_{S,f_i} - I_{S,f_j}\right)
TEC≈αfi,fj40.3×1016(IS,fi−IS,fj)TEC \approx \frac{\alpha_{f_i, f_j}}{40.3\times 10^{16}} \left( I_{S,f_i} - I_{S,f_j}\right)

What can we accomplish with one receiver and 3-frequency GPS measurements?

Most previous work in TEC estimation uses dual-frequency GNSS receiver

  • large receiver networks
  • physical / thin-shell / tomographic ionosphere model

Bias and Error Assumptions

b_{S,f}^\phi \approx b_{S,f}^\rho
bS,fϕ≈bS,fρb_{S,f}^\phi \approx b_{S,f}^\rho
b_{R,f}^\phi \approx b_{R,f}^\rho
bR,fϕ≈bR,fρb_{R,f}^\phi \approx b_{R,f}^\rho

assume no code-carrier bias

\Delta b_{S,f_i,f_j}, \ \Delta b_{R, f_i, f_j}
ΔbS,fi,fj, ΔbR,fi,fj\Delta b_{S,f_i,f_j}, \ \Delta b_{R, f_i, f_j}
  • receiver code-carrier bias usually compensated for by manufacturer

since we will use geometry free combinations, we only care about inter-frequency biases

(IFB)

E\left[ M_{f_i} M_{f_j} \right] \approx 0
E[MfiMfj]≈0E\left[ M_{f_i} M_{f_j} \right] \approx 0
M^\phi \ll M^\rho
Mϕ≪MρM^\phi \ll M^\rho

multipath uncorrelated across different signals

carrier pseudorange noise / multipath is small compared to code

not true

\epsilon^\phi \ll \epsilon^\rho
ϵϕ≪ϵρ\epsilon^\phi \ll \epsilon^\rho
\approx \text{constant}
≈constant\approx \text{constant}

over 1 day

Geometry-Free Combinations

\phi_{S,f_i} - \phi_{S,f_j} = \Delta b_{S,f_i,f_j} + \Delta b_{R,f_i,f_j} - \left(I_{S,f_i} - I_{S,f_j} \right)
ϕS,fi−ϕS,fj=ΔbS,fi,fj+ΔbR,fi,fj−(IS,fi−IS,fj)\phi_{S,f_i} - \phi_{S,f_j} = \Delta b_{S,f_i,f_j} + \Delta b_{R,f_i,f_j} - \left(I_{S,f_i} - I_{S,f_j} \right)
+ \lambda_{f_i}N_{S,f_i} - \lambda_{f_j}N_{S,f_j} + M^\phi_{S,f_i} - M^\phi_{S,f_j} + \epsilon^\phi_{S,f_i} - \epsilon^\phi_{S,f_j}
+λfiNS,fi−λfjNS,fj+MS,fiϕ−MS,fjϕ+ϵS,fiϕ−ϵS,fjϕ+ \lambda_{f_i}N_{S,f_i} - \lambda_{f_j}N_{S,f_j} + M^\phi_{S,f_i} - M^\phi_{S,f_j} + \epsilon^\phi_{S,f_i} - \epsilon^\phi_{S,f_j}
\rho_{S,f} - \phi_{S,f} \approx 2I_{S,f} - \lambda_fN_{S,f} + M_{S,f}^\rho + \epsilon_{S,f}^{\rho}
ρS,f−ϕS,f≈2IS,f−λfNS,f+MS,fρ+ϵS,fρ\rho_{S,f} - \phi_{S,f} \approx 2I_{S,f} - \lambda_fN_{S,f} + M_{S,f}^\rho + \epsilon_{S,f}^{\rho}
\Delta ADR_{f_i,f_j}
ΔADRfi,fj\Delta ADR_{f_i,f_j}
CMC_f
CMCfCMC_f

Geometry-Free Combinations

We can remove satellite IFB using estimates from IGS

\Delta b_{S,f_i,f_j}
ΔbS,fi,fj\Delta b_{S,f_i,f_j}

We express ionosphere delays in terms of TEC

\Delta ADR_{f_i,f_j} \approx \Delta b_{R,f_i,f_j} - \frac{40.3\times 10^{16}}{\alpha_{f_i,f_j}}TEC
ΔADRfi,fj≈ΔbR,fi,fj−40.3×1016αfi,fjTEC\Delta ADR_{f_i,f_j} \approx \Delta b_{R,f_i,f_j} - \frac{40.3\times 10^{16}}{\alpha_{f_i,f_j}}TEC
+ \lambda_{f_i} N_{S,f_i} - \lambda_{f_j} N_{S,f_j} + \cdots
+λfiNS,fi−λfjNS,fj+⋯+ \lambda_{f_i} N_{S,f_i} - \lambda_{f_j} N_{S,f_j} + \cdots
CMC_f \approx \frac{40.3\times 10^{16}}{f^2}TEC - \lambda_f N_{S,f} + \cdots
CMCf≈40.3×1016f2TEC−λfNS,f+⋯CMC_f \approx \frac{40.3\times 10^{16}}{f^2}TEC - \lambda_f N_{S,f} + \cdots

multipath / noise / unmodeled errors

ILS TEC Estimation

Use iterative least-squares to solve large sparse system for 1 day of data

Experiment Data

GPS Lab high-rate GNSS data collection network

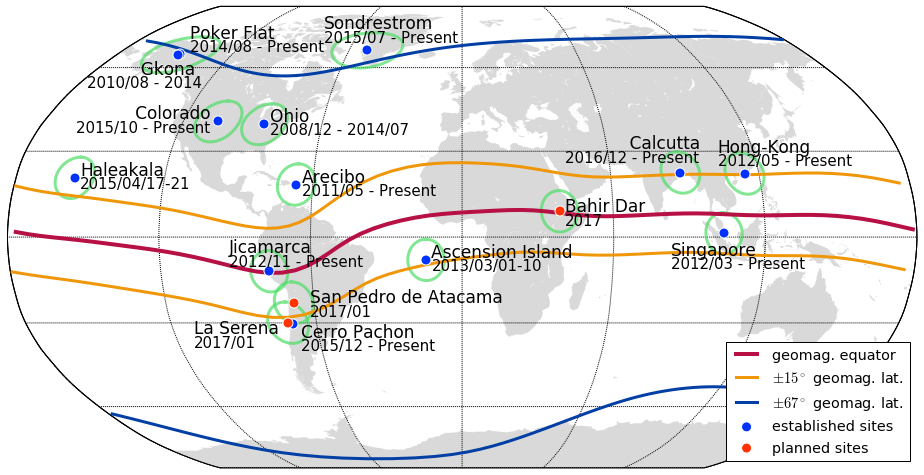
  • 3-receiver array near Poker Flat, Alaska
  • 2016 / 04 / 15
  • Septentrio PolarXs
  • 1 Hz GPS L1/L2/L5 measurements

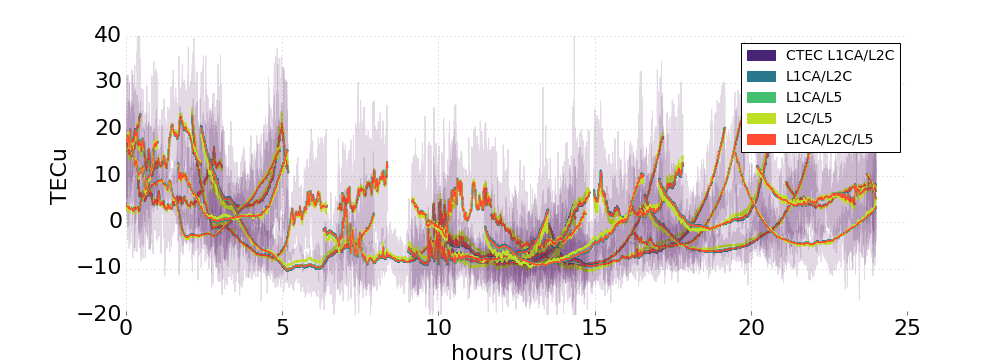
TEC Leveling

Estimated TEC is too low due to direct trade-off between TEC and IFB biases

Some ionosphere constraint or model must be imposed in order to estimate actual IFB

vTEC Gradient-Mapping Method

Assume ionosphere vertical TEC can be described by a linear 2D gradient near receiver

Solve sparse linear system of code-minus-carrier and ADR difference observables

See Harrison Bourne thesis (2016)

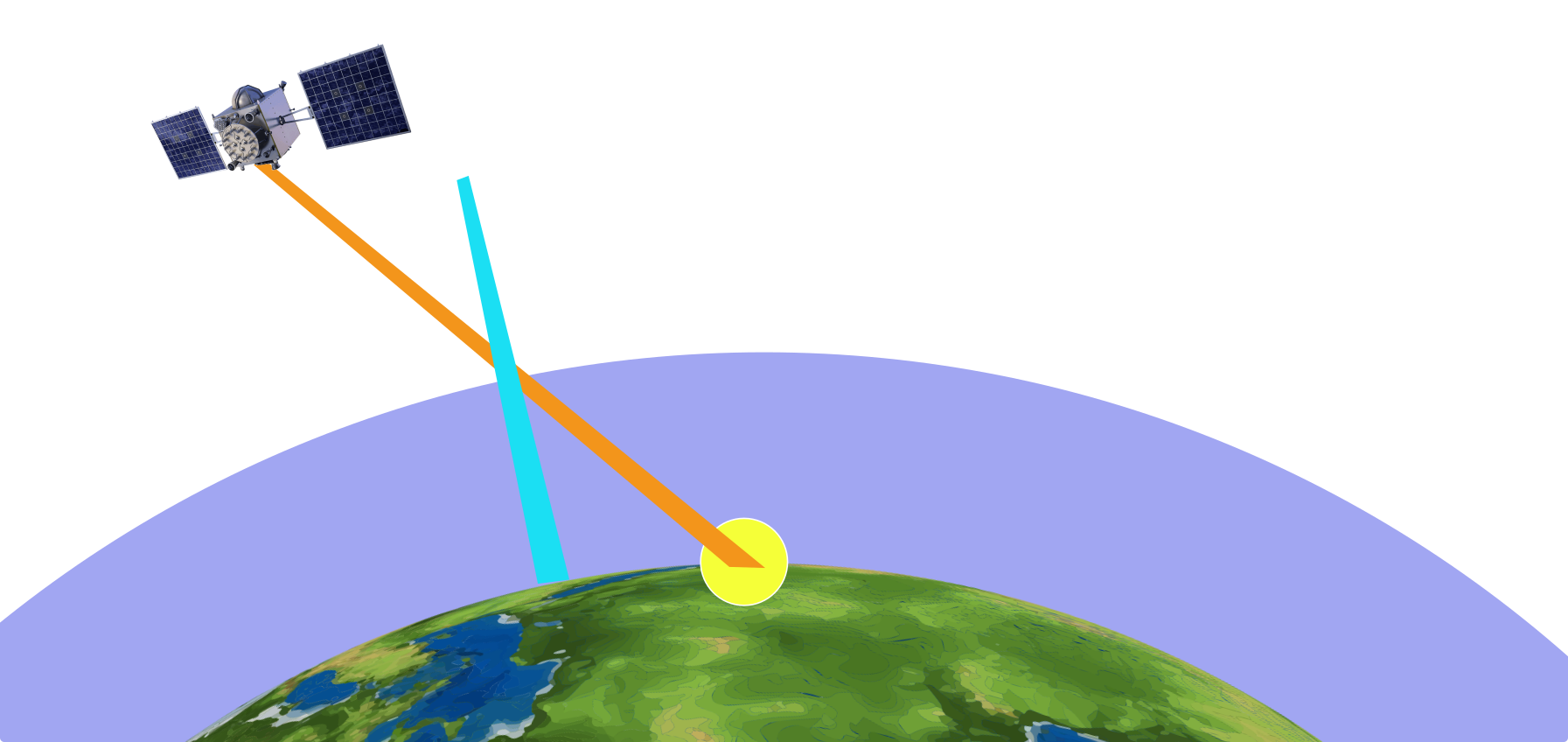
vTEC

TEC

delta lat/lon

Method Summary

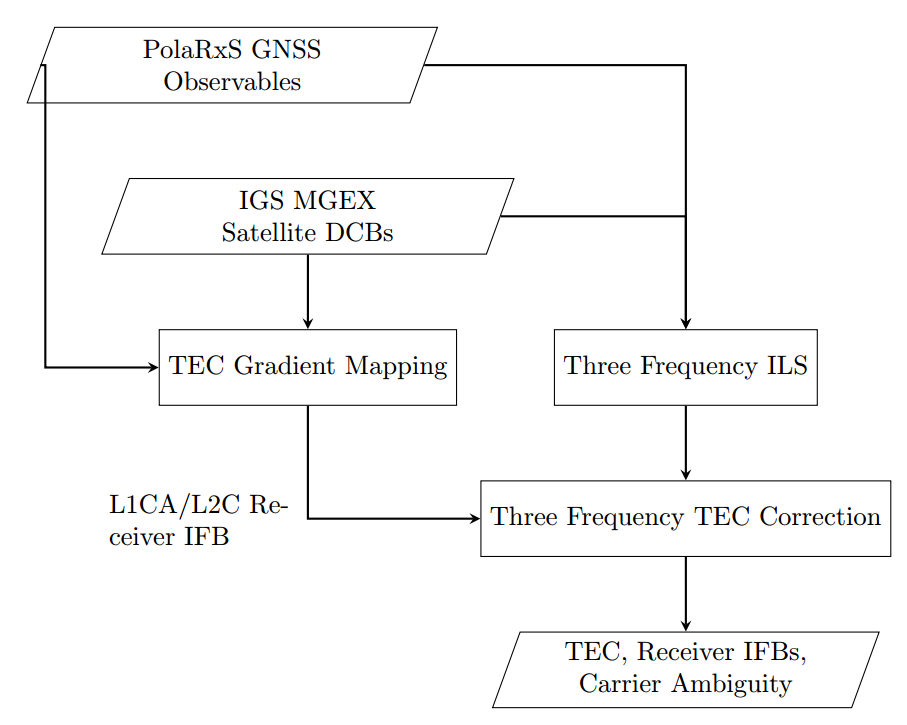
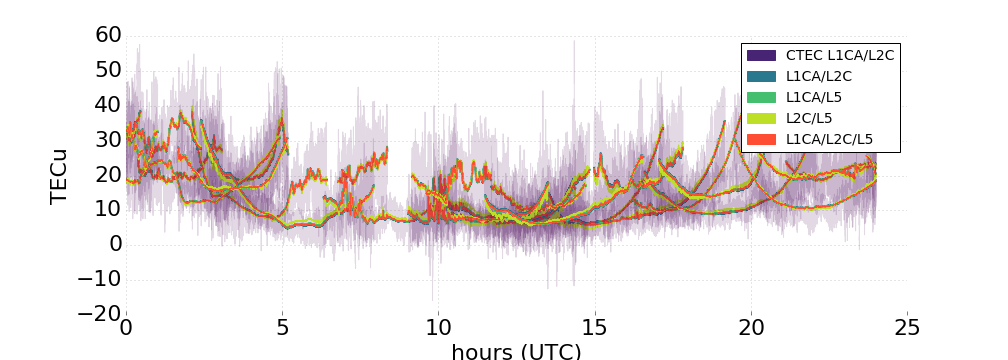
Results

2016 / 04 / 30 - Antenna 1

Full day summary shows physically reasonable TEC levels

Results

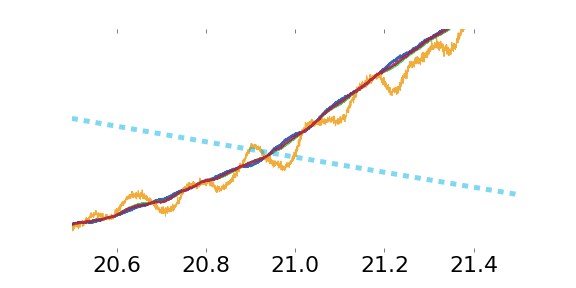
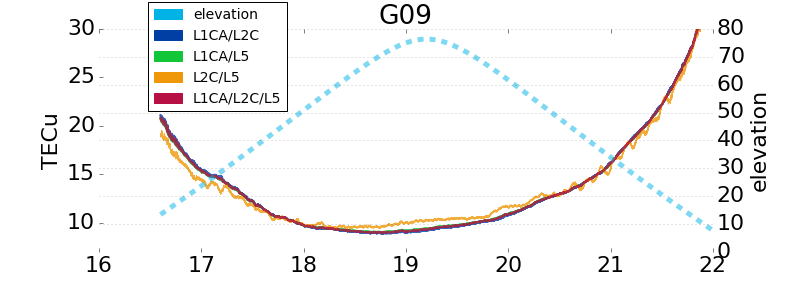
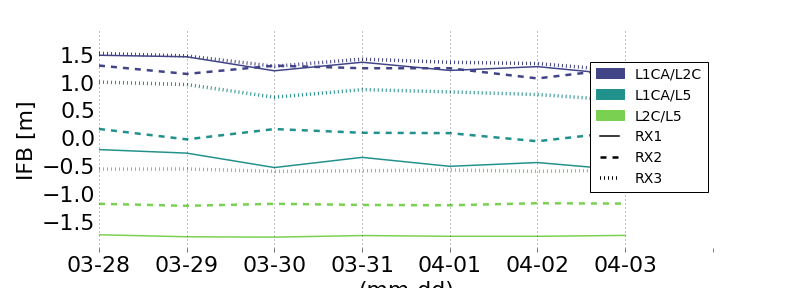
Results

Shows relatively stable receiver IFBs over 7 days

Results

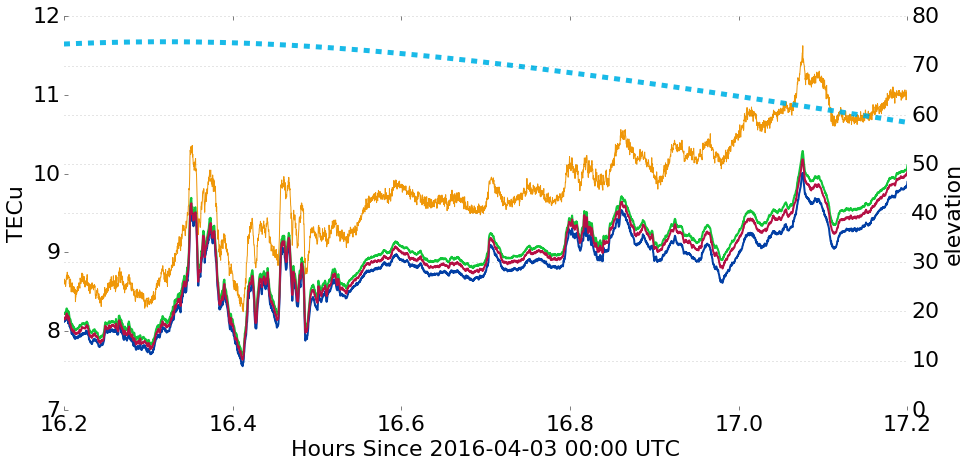
PRN 08 showing high-elevation structure

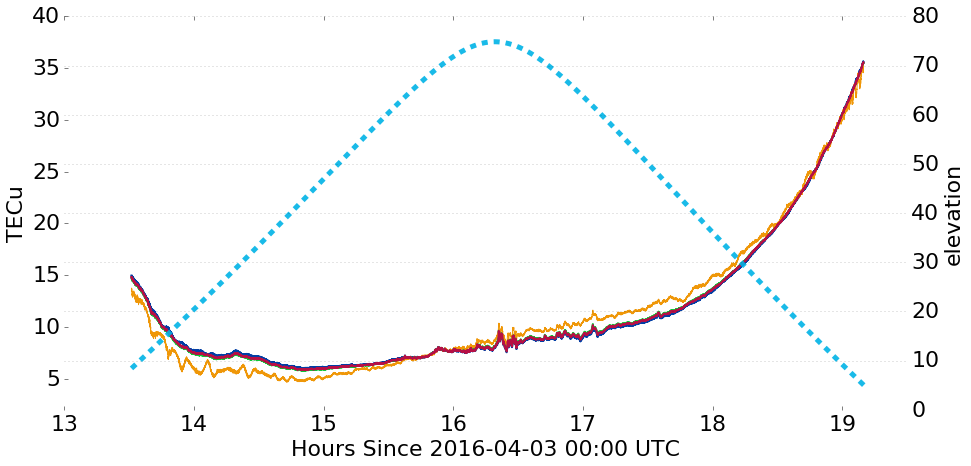
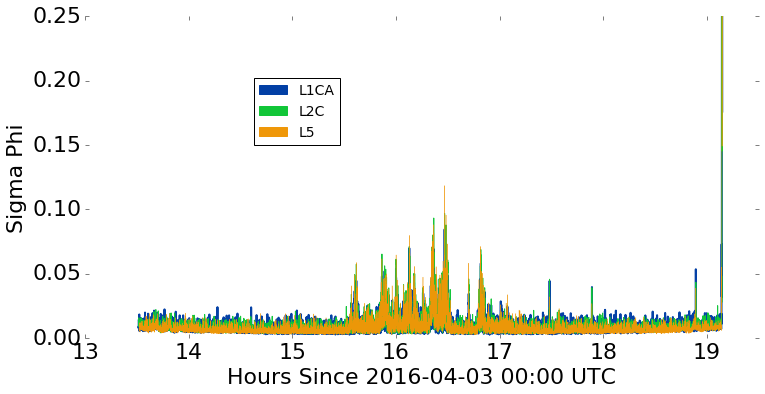
Results

(close-ups of previous slide)

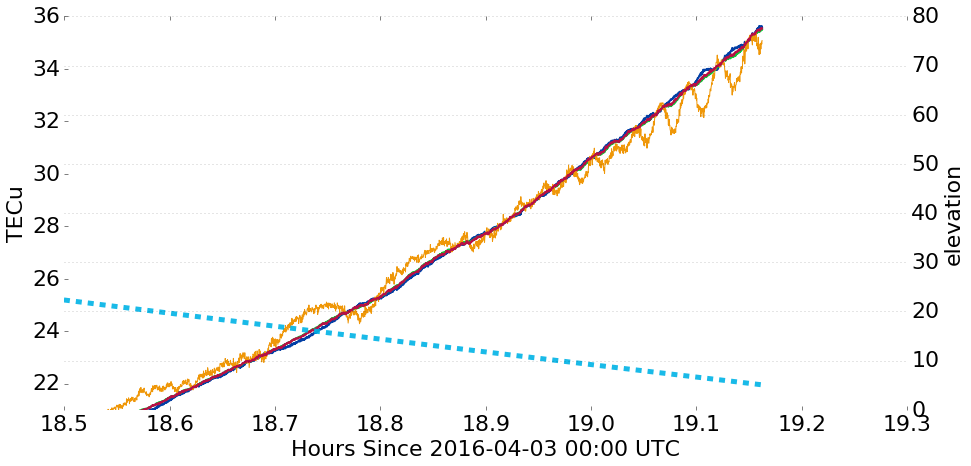
Conclusions

  • demonstrated method to estimate TEC, receiver IFBs, and carrier ambiguities using 3-frequency GPS signals
  • vTEC Gradient-Mapping method was used as the ionosphere constraint in order to receiver IFB bias
  • TEC appears leveled to physically reasonable values
  • receiver IFBs appear stable over several days
  • algorithm is useful for first-step analysis into the origin of remaining errors between TEC computed using 2 frequencies

Future Work

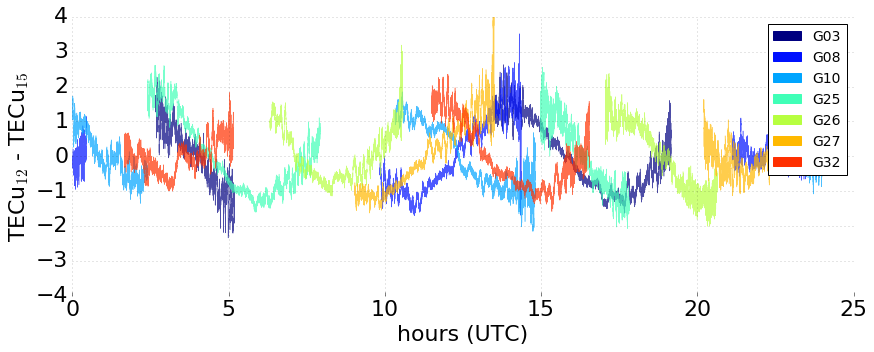
What causes errors?

  • satellite pass / geometry
    • antenna azimuth effects
    • phase wind-up
  • ???

Acknowledgements

This research was supported by the Air Force Research Laboratory and NASA.

References

Spits, Justine. Total Electron Content reconstruction using triple frequency GNSS signals. Diss. Université de Liège,​​ Belgique, 2012.

 

Bourne, Harrison W. An algorithm for accurate ionospheric total electron content and receiver bias estimation using GPS measurements. Diss. Colorado State University. Libraries, 2016.