Analysis of Carrier Phase Residual Trend Variations 

Brian Breitsch\(^1\)

Jade Morton\(^1\)

Using the Geometry-Ionosphere-Free Combination

SAINT Update 2017

1. University of Colorado Boulder

Motivation:

TEC and Triple-Frequency

Background:

Linear Estimation of GNSS Parameters

Main Topic:

Geometry-Ionosphere-Free Combination

Analysis and Results:

GIFC From Real GPS Data

Motivation:

TEC and Triple-Frequency

Background:

Linear Estimation of GNSS Parameters

Main Topic:

Geometry-Ionosphere-Free Combination

Analysis and Results:

GIFC From Real GPS Data

Carrier Phase and TEC

\Phi_i = r + c\Delta t + T + I_i + \lambda_i N_i + H_i + S_i + \epsilon_i
Φi=r+cΔt+T+Ii+λiNi+Hi+Si+ϵi \Phi_i = r + c\Delta t + T + I_i + \lambda_i N_i + H_i + S_i + \epsilon_i

HARDWARE BIASES

IONOSPHERE RANGE ERROR

CARRIER AMBIGUITY

SYSTEMATIC ERRORS / MULTIPATH

FREQUENCY INDEPENDENT EFFECTS

STOCHASTIC ERRORS

frequency \(f_i\)

I_i \approx -\frac{\kappa}{f_i^2} \text{TEC}
Ii≈−κfi2TECI_i \approx -\frac{\kappa}{f_i^2} \text{TEC}

plasma / free electrons

Multi-Frequency GNSS

  • GPS Block IIF / Block III
  • Galileo (E1, E5a/b)
  • GLONASS-K2
Signal Frequency (GHz)
L1CA 1.57542
L2C 1.2276
L5 1.17645

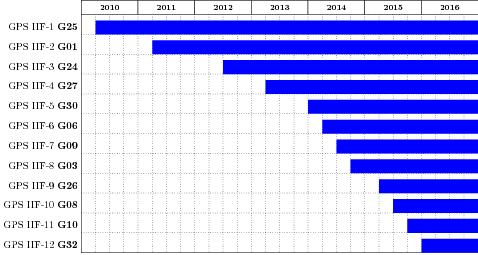
triple-frequency GPS

12 satellites since 2016

Estimation of \(G\) and \(\text{TEC}\) Using Dual-Frequency GNSS

\text{TEC} = \displaystyle -\frac{\Phi_1 - \Phi_2}{\kappa \left(\frac{1}{f_1^2} - \frac{1}{f_2^2}\right)}
TEC=−Φ1−Φ2κ(1f12−1f22)\text{TEC} = \displaystyle -\frac{\Phi_1 - \Phi_2}{\kappa \left(\frac{1}{f_1^2} - \frac{1}{f_2^2}\right)}
G = \displaystyle \frac{f_1^2 \Phi_1 - f_2^2 \Phi_2}{f_1^2 - f_2^2}
G=f12Φ1−f22Φ2f12−f22G = \displaystyle \frac{f_1^2 \Phi_1 - f_2^2 \Phi_2}{f_1^2 - f_2^2}

ionosphere-free combination

geometry-free combination

\Phi_i = G + I_i + S_i + \epsilon_i
Φi=G+Ii+Si+ϵi\Phi_i = G + I_i + S_i + \epsilon_i

"geometry" term

\Phi_i = r + c\Delta t + T + I_i + \lambda_i N_i + H_i + S_i + \epsilon_i
Φi=r+cΔt+T+Ii+λiNi+Hi+Si+ϵi \Phi_i = r + c\Delta t + T + I_i + \lambda_i N_i + H_i + S_i + \epsilon_i

we can solve bias terms

Examples of Two Dual-Frequency TEC Estimates

Poker Flat, Alaska, 2016-01-02

Can we characterize / find the source of these discrepancies?

Motivation:

TEC and Triple-Frequency

Background:

Linear Estimation of GNSS Parameters

Main Topic:

Geometry-Ionosphere-Free Combination

Analysis and Results:

GIFC From Real GPS Data

model parameters

\mathbf{\Phi} = \left[\Phi_1, \cdots, \Phi_m\right]^T
Φ=[Φ1,⋯,Φm]T\mathbf{\Phi} = \left[\Phi_1, \cdots, \Phi_m\right]^T
\mathbf{m} = \left[G, \text{TEC}, S_1, \cdots, S_m \right]^T
m=[G,TEC,S1,⋯,Sm]T\mathbf{m} = \left[G, \text{TEC}, S_1, \cdots, S_m \right]^T
\mathbf{\Phi} = \mathbf{A} \mathbf{m} + \mathbf{\epsilon}
Φ=Am+ϵ\mathbf{\Phi} = \mathbf{A} \mathbf{m} + \mathbf{\epsilon}

Linear Inverse Problem

observations

\Phi_i = G + I_i + S_i + \epsilon_i
Φi=G+Ii+Si+ϵi\Phi_i = G + I_i + S_i + \epsilon_i
\mathbf{\hat{m}} \approx \mathbf{A^*} \mathbf{\Phi}
m^≈A∗Φ\mathbf{\hat{m}} \approx \mathbf{A^*} \mathbf{\Phi}

estimate:

\mathbf{A^*} =\begin{bmatrix} \mathbf{C}_G \\ \mathbf{C}_\text{TEC} \\ \mathbf{C}_{S_1} \\ \vdots \\ \mathbf{C}_{S_m} \end{bmatrix}
A∗=[CGCTECCS1⋮CSm]\mathbf{A^*} =\begin{bmatrix} \mathbf{C}_G \\ \mathbf{C}_\text{TEC} \\ \mathbf{C}_{S_1} \\ \vdots \\ \mathbf{C}_{S_m} \end{bmatrix}

geometry estimator

TEC estimator

systematic-error estimators

Linear Coefficient Constraints

\sum_i c_i = 0
∑ici=0\sum_i c_i = 0
\sum_i c_i = 1
∑ici=1\sum_i c_i = 1

geometry-free

geometry-estimator

\sum_i -\frac{\kappa}{f_i^2}c_i = 1
∑i−κfi2ci=1\sum_i -\frac{\kappa}{f_i^2}c_i = 1
\sum_i \frac{c_i}{f_i^2} = 0
∑icifi2=0\sum_i \frac{c_i}{f_i^2} = 0

TEC-estimator

ionosphere-free

\Phi_i = G + I_i + S_i + \epsilon_i
Φi=G+Ii+Si+ϵi\Phi_i = G + I_i + S_i + \epsilon_i

solutions at intersection of constraint hyperplanes

|G| , |I_i| \gg |S_i|
∣G∣,∣Ii∣≫∣Si∣|G| , |I_i| \gg |S_i|

a-priori information:

Estimators

\(\text{TEC}\) Estimator

TEC-estimator + geometry-free constraints

\(G\) Estimator

geometry-estimator + ionosphere-free constraints

\(\text{L1,L2,L5}\)

\(\text{L1,L5}\)

\(\text{L1,L2}\)

choose min-norm

Triple-Frequency GPS Estimator Coefficients

\begin{matrix} \text{Estimate} & c_1 & c_2 & c_3 & \text{noise amp.} \\[.5em] G_\text{L1,L2,L5} & 2.3 & -0.4 & -1.0 & 2.5 \\ G_\text{L1,L5} & 2.3 & 0 & -1.3 & 2.6 \\ G_\text{L1,L2} & 2.5 & -1.5 & 0 & 3.0 \\ G_\text{L2,L5} & 0 & 12.3 & -11.3 & 16.6 \end{matrix}
Estimatec1c2c3noise amp.GL1,L2,L52.3−0.4−1.02.5GL1,L52.30−1.32.6GL1,L22.5−1.503.0GL2,L5012.3−11.316.6\begin{matrix} \text{Estimate} & c_1 & c_2 & c_3 & \text{noise amp.} \\[.5em] G_\text{L1,L2,L5} & 2.3 & -0.4 & -1.0 & 2.5 \\ G_\text{L1,L5} & 2.3 & 0 & -1.3 & 2.6 \\ G_\text{L1,L2} & 2.5 & -1.5 & 0 & 3.0 \\ G_\text{L2,L5} & 0 & 12.3 & -11.3 & 16.6 \end{matrix}
\begin{matrix} \text{Estimate} & c_1 & c_2 & c_3 & \text{noise amp.} \\[.5em] \text{TEC}_\text{L1,L2,L5} & 8.3 & -2.9 & -5.4 & 10.3 & \\ \text{TEC}_\text{L1,L5} & 7.8 & 0 & -7.8 & 11.0 & \\ \text{TEC}_\text{L1,L2} & 9.5 & -9.5 & 0 & 13.5 & \\ \text{TEC}_\text{L2,L5} & 0 & 42.1 & -42.1 & 59.5 & \end{matrix}
Estimatec1c2c3noise amp.TECL1,L2,L58.3−2.9−5.410.3TECL1,L57.80−7.811.0TECL1,L29.5−9.5013.5TECL2,L5042.1−42.159.5\begin{matrix} \text{Estimate} & c_1 & c_2 & c_3 & \text{noise amp.} \\[.5em] \text{TEC}_\text{L1,L2,L5} & 8.3 & -2.9 & -5.4 & 10.3 & \\ \text{TEC}_\text{L1,L5} & 7.8 & 0 & -7.8 & 11.0 & \\ \text{TEC}_\text{L1,L2} & 9.5 & -9.5 & 0 & 13.5 & \\ \text{TEC}_\text{L2,L5} & 0 & 42.1 & -42.1 & 59.5 & \end{matrix}

\(G\) Estimator

\(\text{TEC}\) Estimator

Triple-Frequency TEC Estimate Examples

Motivation:

TEC and Triple-Frequency

Background:

Linear Estimation of GNSS Parameters

Main Topic:

Geometry-Ionosphere-Free Combination

Analysis and Results:

GIFC From Real GPS Data

Estimating Systematic Errors

apply both geometry-free and ionosphere-free constraints

For triple-frequency GNSS:

\begin{aligned} c_1 & = \ \ x \frac{\frac{1}{f_3^2} - \frac{1}{f_2^2}}{\frac{1}{f_2^2} - \frac{1}{f_1^2}} \\[1em] c_2 & = - x \frac{\frac{1}{f_3^2} - \frac{1}{f_1^2}}{\frac{1}{f_2^2} - \frac{1}{f_1^2}} \\[1em] c_3 & = \ \ x \end{aligned}
c1=  x1f32−1f221f22−1f12c2=−x1f32−1f121f22−1f12c3=  x\begin{aligned} c_1 & = \ \ x \frac{\frac{1}{f_3^2} - \frac{1}{f_2^2}}{\frac{1}{f_2^2} - \frac{1}{f_1^2}} \\[1em] c_2 & = - x \frac{\frac{1}{f_3^2} - \frac{1}{f_1^2}}{\frac{1}{f_2^2} - \frac{1}{f_1^2}} \\[1em] c_3 & = \ \ x \end{aligned}

system is linear subspace

there is "only one estimate" of systematic errors

note this requires \(m \ge 3\)

\Phi_i = G + I_i + S_i + \epsilon_i
Φi=G+Ii+Si+ϵi\Phi_i = G + I_i + S_i + \epsilon_i

Geometry-Ionosphere-Free Combination

\mathbf{C}_{\text{TEC}_{1,2,3}}
CTEC1,2,3\mathbf{C}_{\text{TEC}_{1,2,3}}
\mathbf{C}_\text{GIFC}
CGIFC\mathbf{C}_\text{GIFC}

information about systematic and stochastic errors present in GNSS carrier phase observables

\begin{aligned} \mathbf{C}_{\text{GIFC}_\text{L1,L2,L5}} & = \mathbf{C}_{\text{TEC}_{\text{L1,L5}}} - \mathbf{C}_{\text{TEC}_{\text{L1,L2}}} \\[1em] & = \left[-1.756, \ 9.520, \ -7.764\right] \end{aligned}
CGIFCL1,L2,L5=CTECL1,L5−CTECL1,L2=[−1.756, 9.520, −7.764]\begin{aligned} \mathbf{C}_{\text{GIFC}_\text{L1,L2,L5}} & = \mathbf{C}_{\text{TEC}_{\text{L1,L5}}} - \mathbf{C}_{\text{TEC}_{\text{L1,L2}}} \\[1em] & = \left[-1.756, \ 9.520, \ -7.764\right] \end{aligned}

We (arbitrarily) choose:

\Phi_i = G + I_i + S_i + \epsilon_i
Φi=G+Ii+Si+ϵi\Phi_i = G + I_i + S_i + \epsilon_i
\mathbf{C}_{G_{1,2,3}}
CG1,2,3\mathbf{C}_{G_{1,2,3}}

\( \text{GIFC} = G_{1,3} - G_{1,2} \)

\( \text{GIFC} = \text{TEC}_{1,3} - \text{TEC}_{1,2} \)

Motivation:

TEC and Triple-Frequency

Background:

Linear Estimation of GNSS Parameters

Main Topic:

Geometry-Ionosphere-Free Combination

Analysis and Results:

GIFC From Real GPS Data

Experiment Data

Sense Lab high-rate GNSS data collection network

  • Alaska, Hong Kong, Peru
  • 2013 - 2016
  • 1 Hz GPS L1/L2/L5 measurements
  • Septentrio PolarXs

GIFC Examples

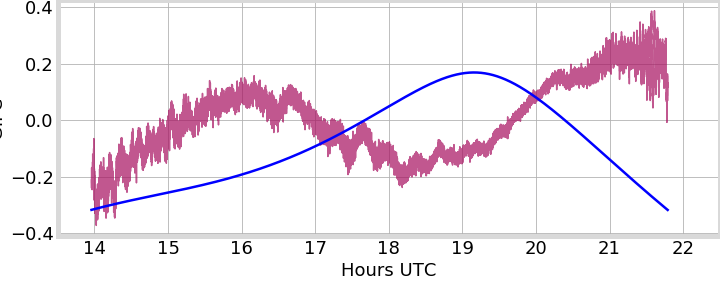
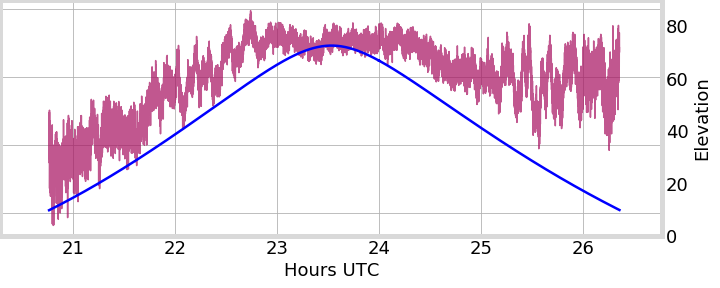
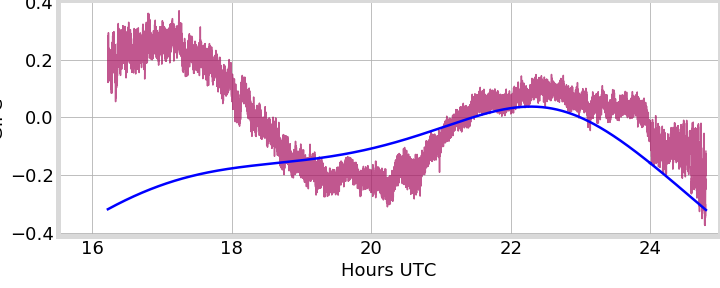
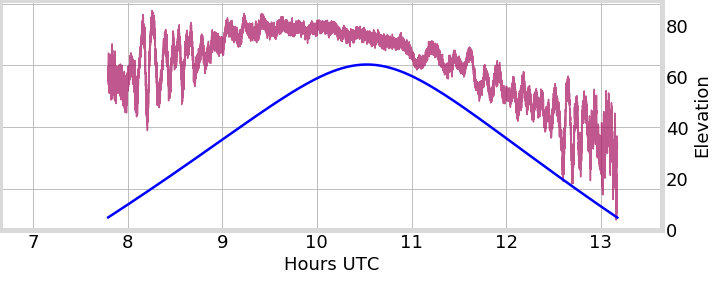
PRN 24, Peru

PRN 24, Hong Kong

PRN 25, Peru

PRN 01, Alaska

2013-01-01

2014-05-15

2013-01-01

2014-06-29

GIFC

Sat. Elevation

GIFC Calendar

PRN 24, Hong Kong

PRN 25, Hong Kong

PRN 24, Alaska

PRN 25, Alaska

GIFC Calendar

PRN 25, Alaska

  • large, long-term GIFC trend likely due mostly to satellite thermal oscillations
  • studied by (Montebruck et. al. 2012) and (Li et. al. 2013)

\(\theta\)

GIFC Histogram

Peru Example

estimate trend \(\Rightarrow\) reduce major component of TEC and G estimate errors

(all satellites, all data)

Conclusions

  • GIFC is an indicator of the presence of systematic / stochastic errors
  • dominant GIFC component is periodic
    • long, arc-wide trend due to satellite thermal variations
    • errors on order of up to 0.5 TECu
  • need to start estimating variable IFB corrections to accommodate TEC / geometry estimates

Next Steps

  • use to analyze other systematic dispersive errors such as multipath and strong scintillation

References

O. Montenbruck, U. Hugentobler, R. Dach, P. Steigenberger, and A. Hauschild, “Apparent clock variations of the Block IIF-1 (SVN62) GPS satellite,” GPS Solutions, vol. 16, no. 3, pp. 303–313, 2012.

 

H. Li, X. Zhou, and B. Wu, “Fast estimation and analysis of the inter-frequency clock bias for Block IIF satellites,” GPS Solutions, vol. 17, no. 3, pp. 347–355, 2013.

 

B. Breitsch, "Optimal Linear Combinations of GNSS Phase Observables to Improve and Assess TEC Estimation Precision," Masters Thesis, Colorado State University

 

Acknowledgements

This research was supported by the Air Force Research Laboratory.