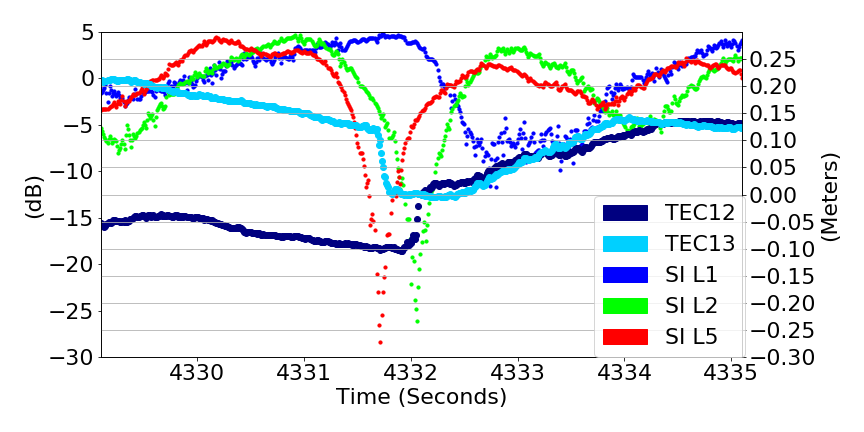
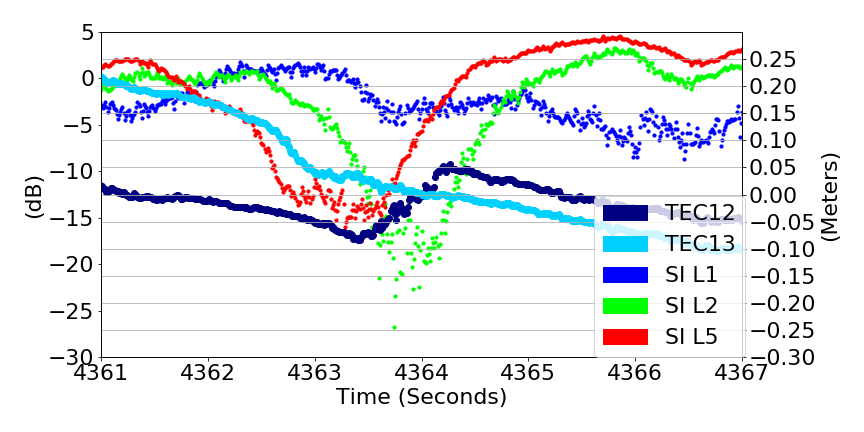
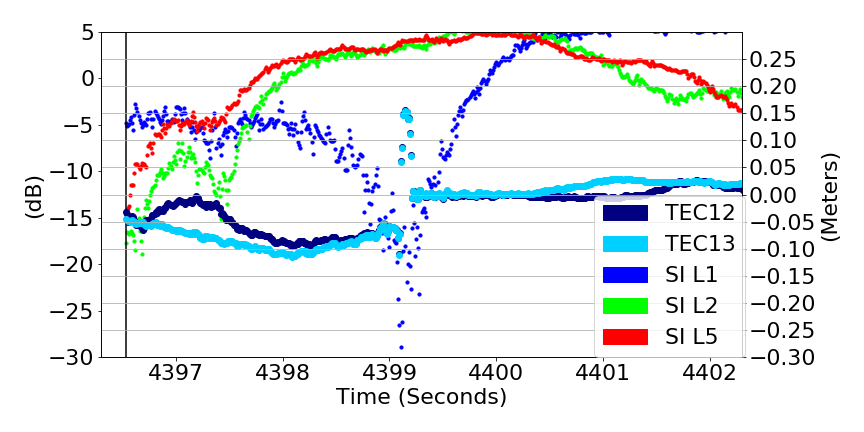
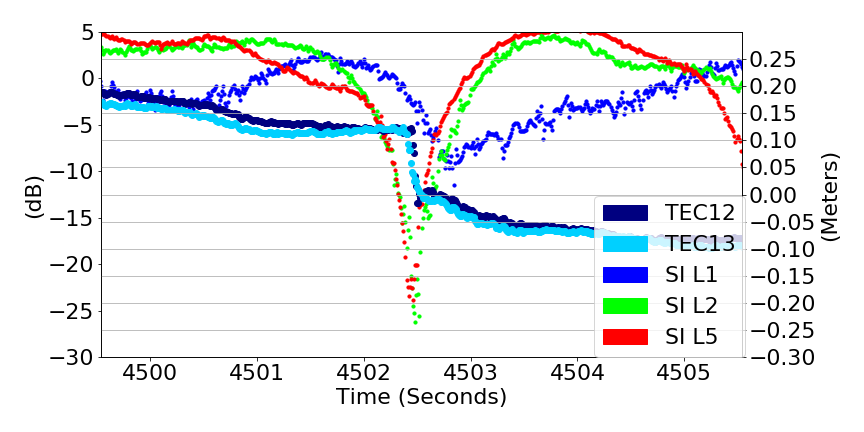
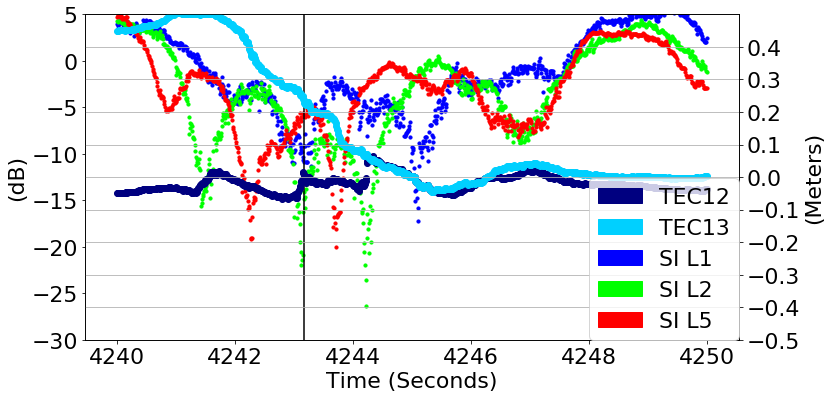
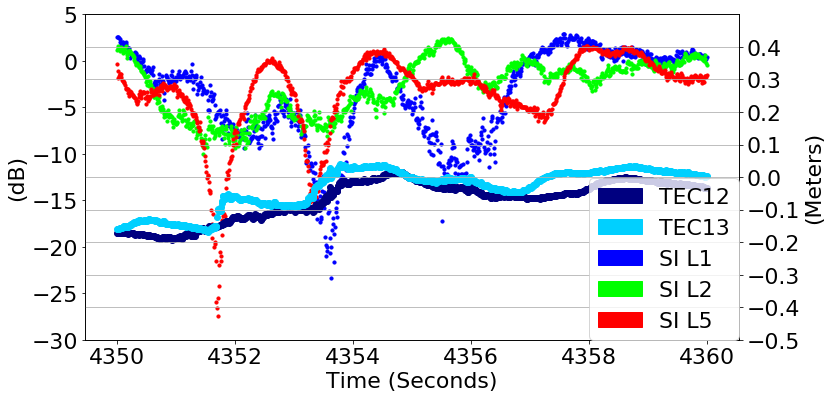
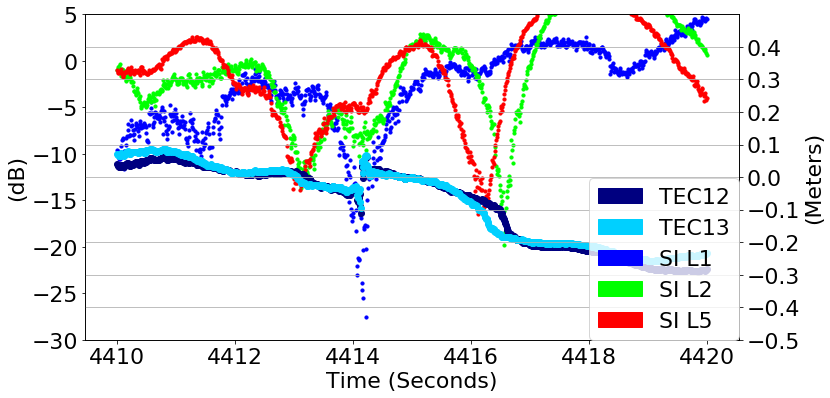
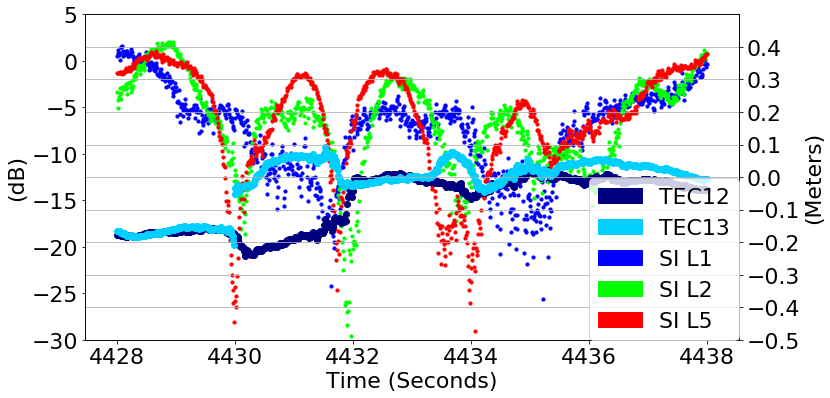
Deep Fades

Brian Breitsch

12 January 2018

Weekly Seminar:

\hat{x}(t) = x(t) + \tilde{x}(t)
x^(t)=x(t)+x~(t)\hat{x}(t) = x(t) + \tilde{x}(t)
= \frac{1}{2} A(t) \exp\left( i \phi(t) \right) \left[ 1 + \frac{\tilde{A}(t)}{A(t)} \exp\left( i \left( \tilde{\phi}(t) - \phi(t) \right) \right) \right]
=12A(t)exp(iϕ(t))[1+A~(t)A(t)exp(i(ϕ~(t)−ϕ(t)))] = \frac{1}{2} A(t) \exp\left( i \phi(t) \right) \left[ 1 + \frac{\tilde{A}(t)}{A(t)} \exp\left( i \left( \tilde{\phi}(t) - \phi(t) \right) \right) \right]
= \frac{1}{2} A(t) \exp\left( i \phi(t) \right) + \frac{1}{2} \tilde{A}(t) \exp\left( i \tilde{\phi}(t) \right)
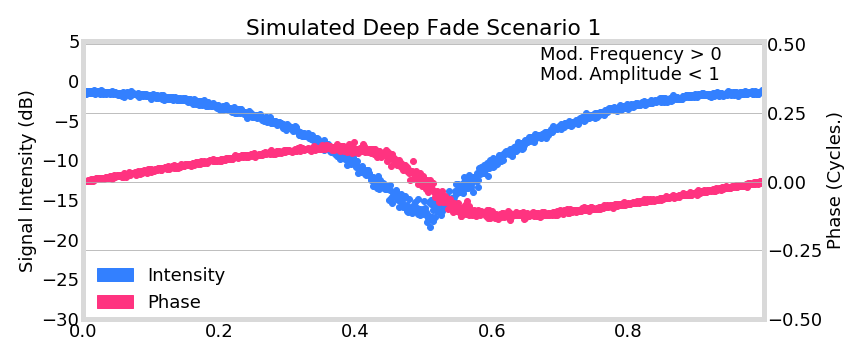
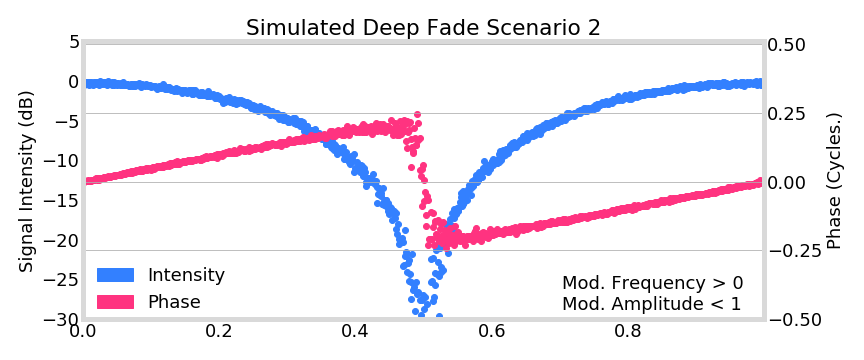
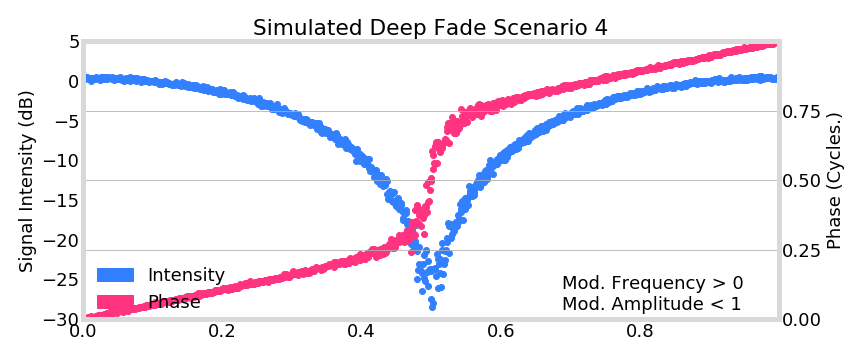
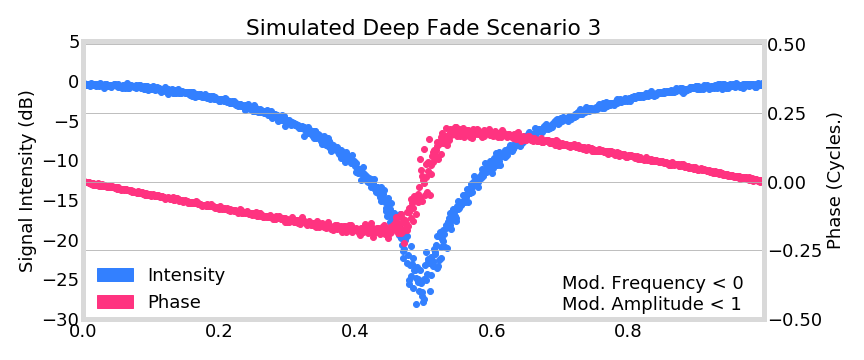
=12A(t)exp(iϕ(t))+12A~(t)exp(iϕ~(t)) = \frac{1}{2} A(t) \exp\left( i \phi(t) \right) + \frac{1}{2} \tilde{A}(t) \exp\left( i \tilde{\phi}(t) \right)
= \frac{1}{2} A(t) \exp\left( i \phi(t) \right) \left[ 1 + \alpha \exp\left( i \Delta \phi \right) \right]
=12A(t)exp(iϕ(t))[1+αexp(iΔϕ)] = \frac{1}{2} A(t) \exp\left( i \phi(t) \right) \left[ 1 + \alpha \exp\left( i \Delta \phi \right) \right]
x(t) = \frac{1}{2} A(t) \exp\left( i \phi(t) \right)
x(t)=12A(t)exp(iϕ(t))x(t) = \frac{1}{2} A(t) \exp\left( i \phi(t) \right)

BASEBAND

COMPLEX MODULATION

ORIGINAL SIGNAL