Distributed Smart Energy Systems

IfA Open House - 3 December 2018

New technologies for power generation from renewable energy sources

Ready for 100% renewables?

What is mature?

What is not?

  • Microgeneration technology
  • Primary source diversification
  • Incentives and policies
  • Enterprises and investors
  • Real-time grid operation
  • A technology to interconnect renewable sources
  • A study of the stability/performance of the system

The Smart Grid challenge:

innovate the largest machine ever built by man

Virtual inertia for

increased frequency stability

Traditional grid:

massive mechanical inertia that automatically compensates for power imbalance

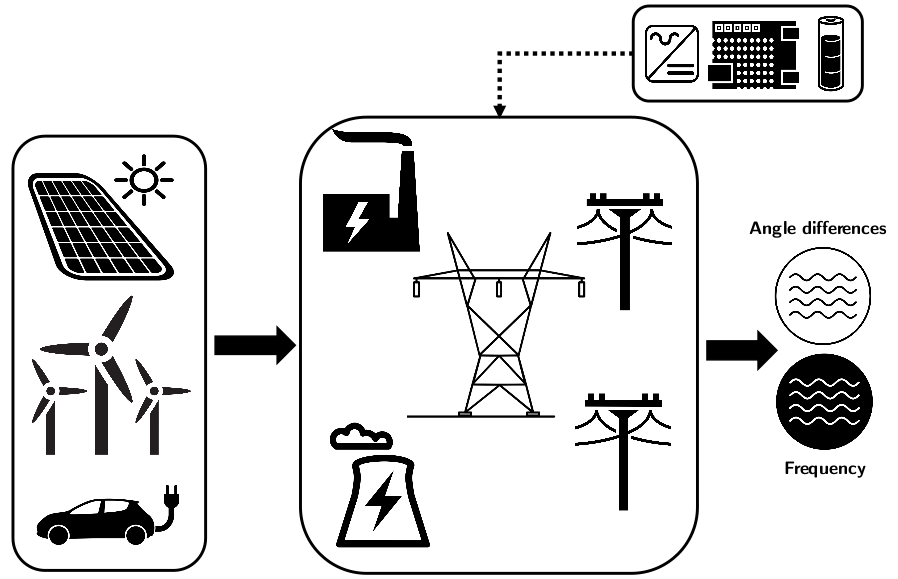
Future grid:

larger power imbalance
less mechanical inertia
one solution:
virtual inertia

Virtual inertia = real energy storage + power converter

\displaystyle \min \int_0^\infty \left( \sum_{ij} \alpha_{ij} (\theta_i(t) - \theta_j(t))^2 + \sum_i \beta_i \dot \theta_i(t)^2 \right) dt
min⁡∫0∞(∑ijαij(θi(t)−θj(t))2+∑iβiθ˙i(t)2)dt\displaystyle \min \int_0^\infty \left( \sum_{ij} \alpha_{ij} (\theta_i(t) - \theta_j(t))^2 + \sum_i \beta_i \dot \theta_i(t)^2 \right) dt
\displaystyle M_i \ddot \theta_i + D_i \dot \theta_i = {P_i}^\text{in} - {P_i}^\text{out}
Miθ¨i+Diθ˙i=Piin−Piout\displaystyle M_i \ddot \theta_i + D_i \dot \theta_i = {P_i}^\text{in} - {P_i}^\text{out}

Swing eq.

Goal:

Advanced methods for numerical optimization

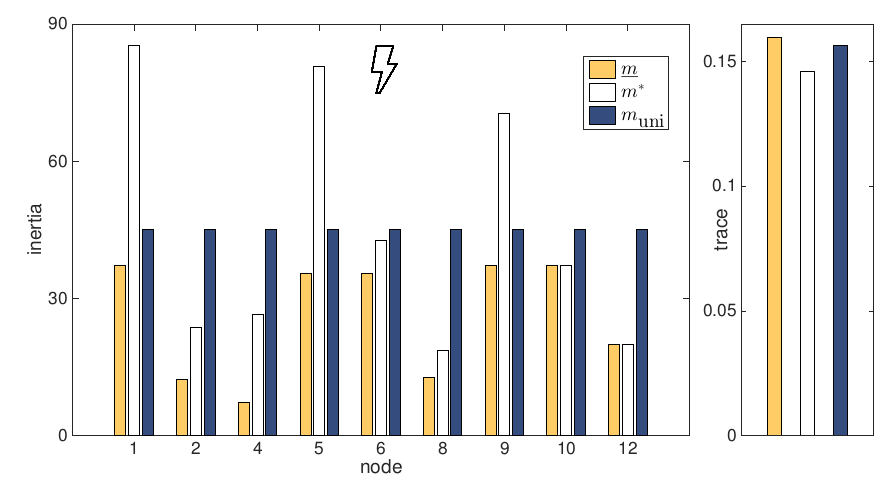
Analysis of a zero-inertia grid:
phasor-free models

Most power system models implicitly assume

quasi-sinusoidal operation at the nominal frequency

We need a model without these assumptions!

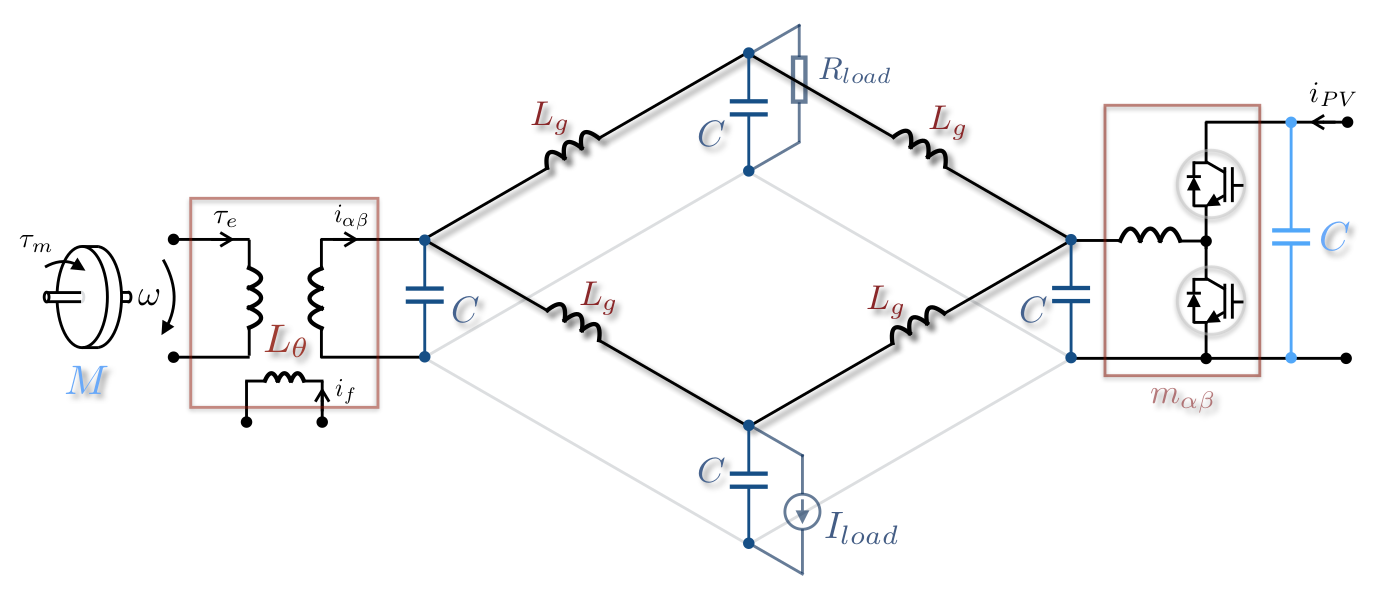
Synchronous generators

Power
converters

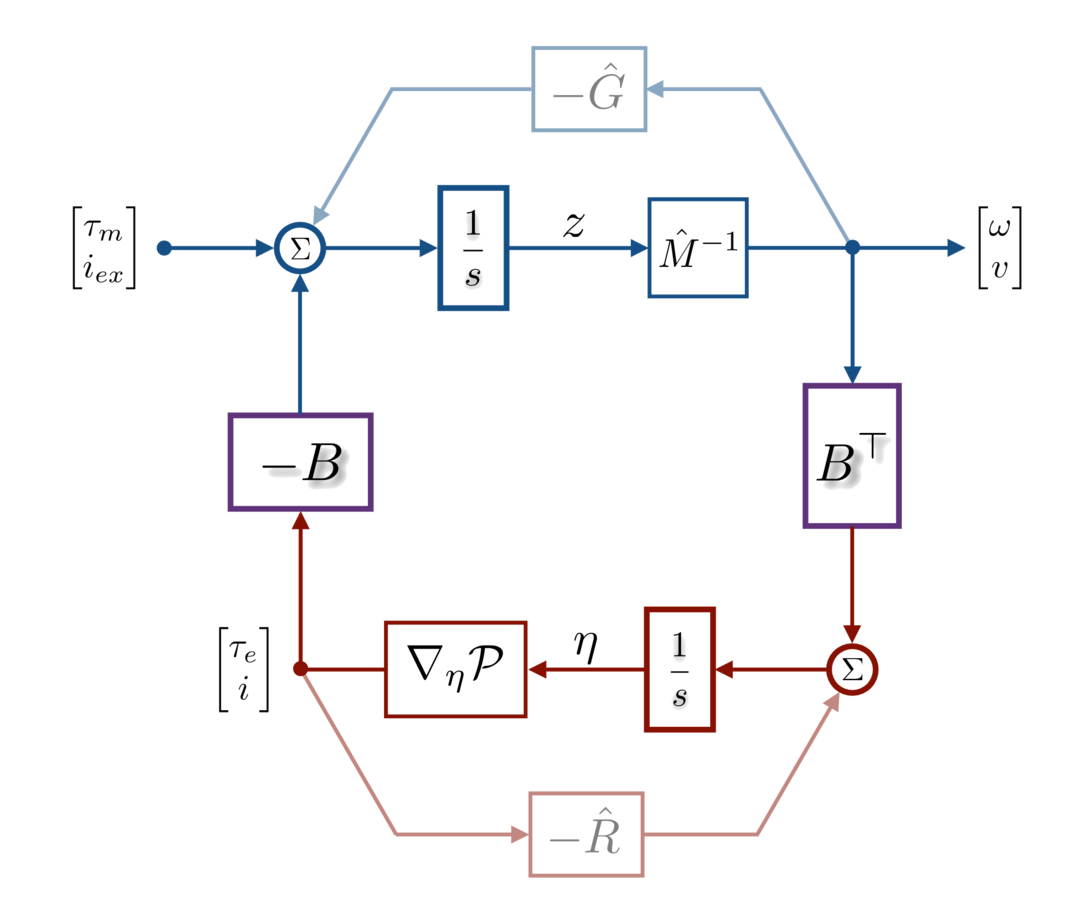
A port-Hamiltonian model for the power grid:

  • explicit modeling of energy balance
  • network of subsystems
  • powerful tools for the analysis of the interconnection

A model for the design of new generation of grid controllers

Mathematical modeling

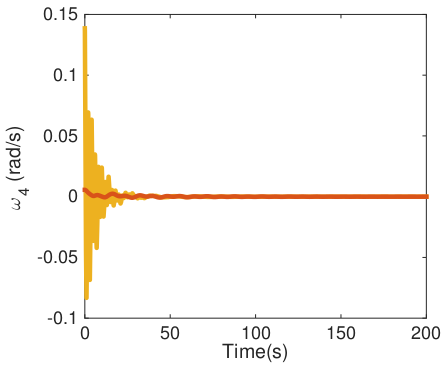
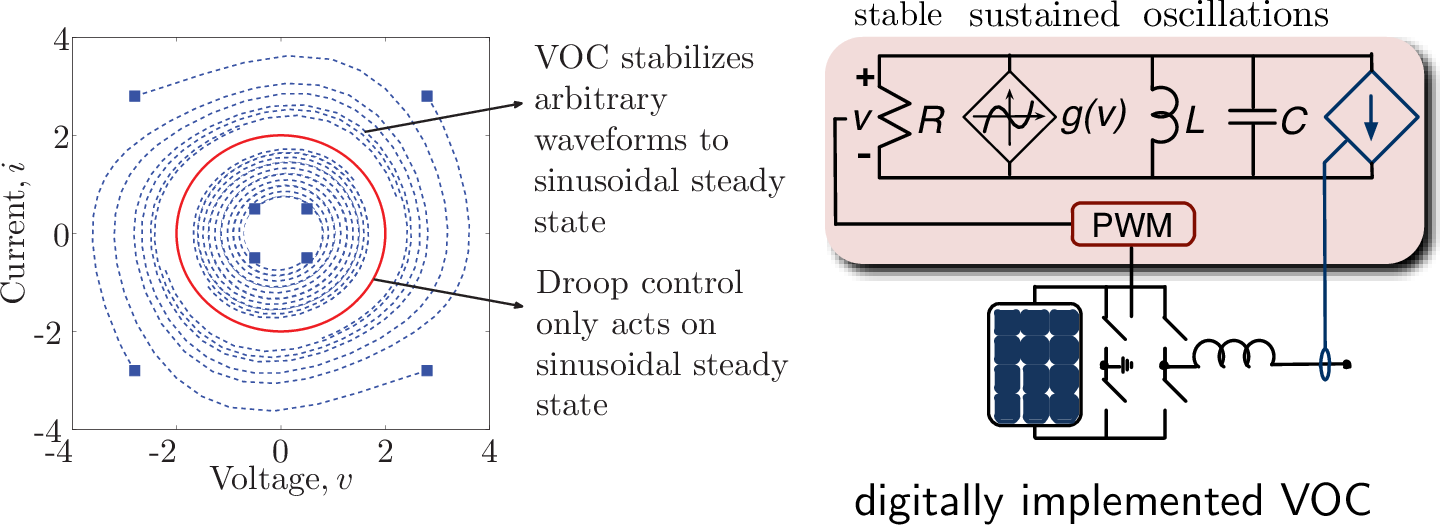
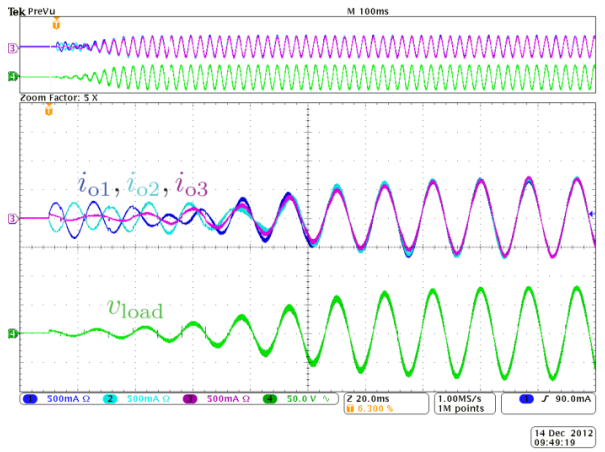
Synchronization in a zero-inertia grid:
virtual oscillators

How to synchronize power inverters?

Do we need to emulate synchronous generators? 

Emerging limit cycles in nonlinear systems!

Nonlinear control design

Real-time power flow optimization

Typical grid optimization problem

\displaystyle \min_{v, \theta, p, q} \sum_i c_i(p_i)
min⁡v,θ,p,q∑ici(pi)\displaystyle \min_{v, \theta, p, q} \sum_i c_i(p_i)

sum of power generation costs

{p_i}^\text{min} \le {p_i} \le {p_i}^\text{max}
pimin≤pi≤pimax{p_i}^\text{min} \le {p_i} \le {p_i}^\text{max}
{v_i}^\text{min} \le {v_i} \le {v_i}^\text{max}
vimin≤vi≤vimax{v_i}^\text{min} \le {v_i} \le {v_i}^\text{max}

power generation limits

voltage contraints

\sqrt{{p_i}^2 + {q_i}^2} \le {s_i}^\text{max}
pi2+qi2≤simax\sqrt{{p_i}^2 + {q_i}^2} \le {s_i}^\text{max}

thermal generator limits

v_i \sum_j v_i (g_{ij} \cos (\theta_i -\theta_j) + b_{ij} \sin (\theta_i -\theta_j) ) = p_i
vi∑jvi(gijcos⁡(θi−θj)+bijsin⁡(θi−θj))=piv_i \sum_j v_i (g_{ij} \cos (\theta_i -\theta_j) + b_{ij} \sin (\theta_i -\theta_j) ) = p_i
v_i \sum_j v_i (g_{ij} \sin (\theta_i -\theta_j) - b_{ij} \cos (\theta_i -\theta_j) ) = q_i
vi∑jvi(gijsin⁡(θi−θj)−bijcos⁡(θi−θj))=qiv_i \sum_j v_i (g_{ij} \sin (\theta_i -\theta_j) - b_{ij} \cos (\theta_i -\theta_j) ) = q_i

power flow eq's!

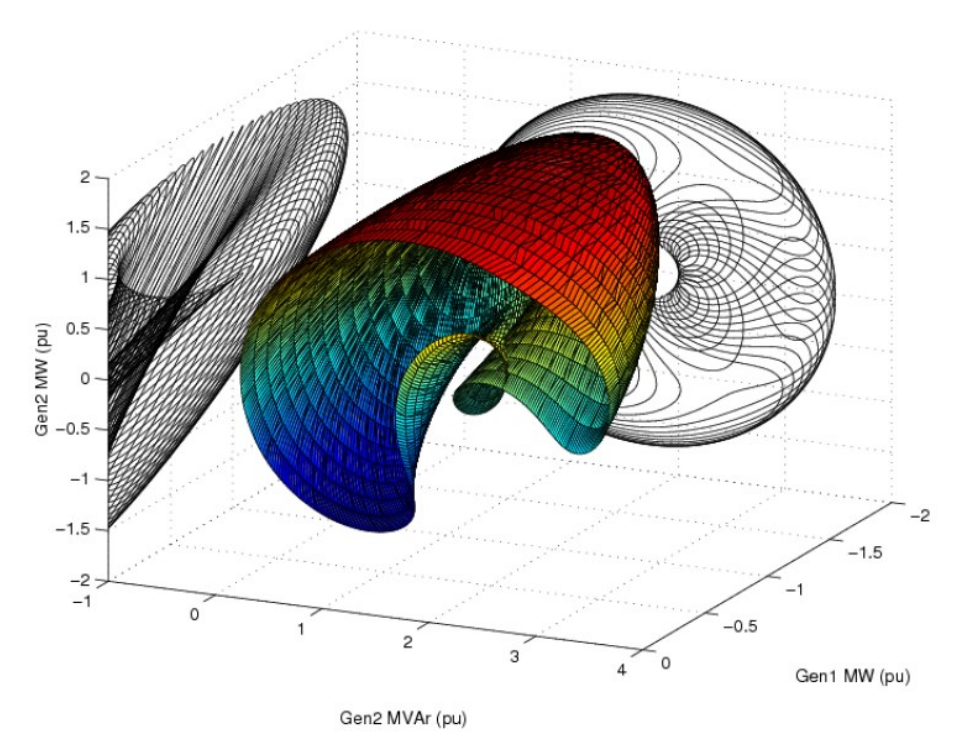
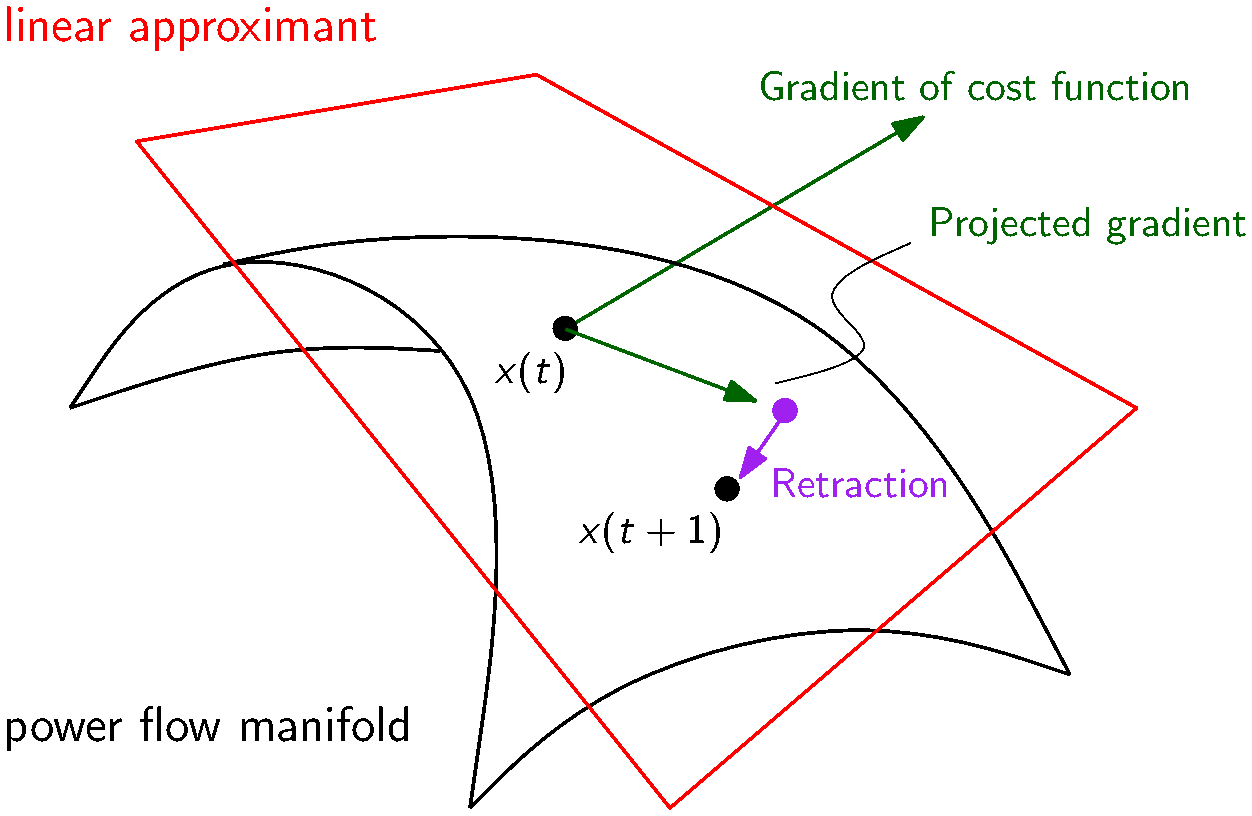
A highly nonconvex manifold!

 

Geometric methods for iterative optimization

Optimization theory

Questions?

Distributed control

Optimization theory

Nonlinear control design

Mathematical modeling

Advanced methods for numerical optimization

Distributed Smart Energy Systems