Investing is a game
A small exercise in Game Theory
for "risk-free" investment
What is Game Theory?
Game Theory is a branch of Applied Mathematics that studies the strategic behavior of rational players in a competitive scenario (game).
Investing can be a game: you (investor) against the world's economy!

Nash Equilibrium
Assume that two Players play their strategy, and after seeing the result, none of them would like to go back and change her strategy (no regret). This is a Nash Equilibrium.
In investing terms, this means investing in one kind of assets so that you are not going to regret your choice, no matter what is the outcome of the market.
As you can imagine, Nash Equilibria of this kind rarely exist...
However...
Mixed Nash Equilibrium
...John Nash (and others) proved that a mixed Nash equilibrium always exists!
If you can invest in multiple strategies at the same time, then there is an "optimal" mixture of strategies.
Sometimes the mixed strategy is completely mixed, which guarantees that the outcome does not depend at all on the other Player's action (that is, the market).
In general, a mixed stategy gives the largest risk-free return
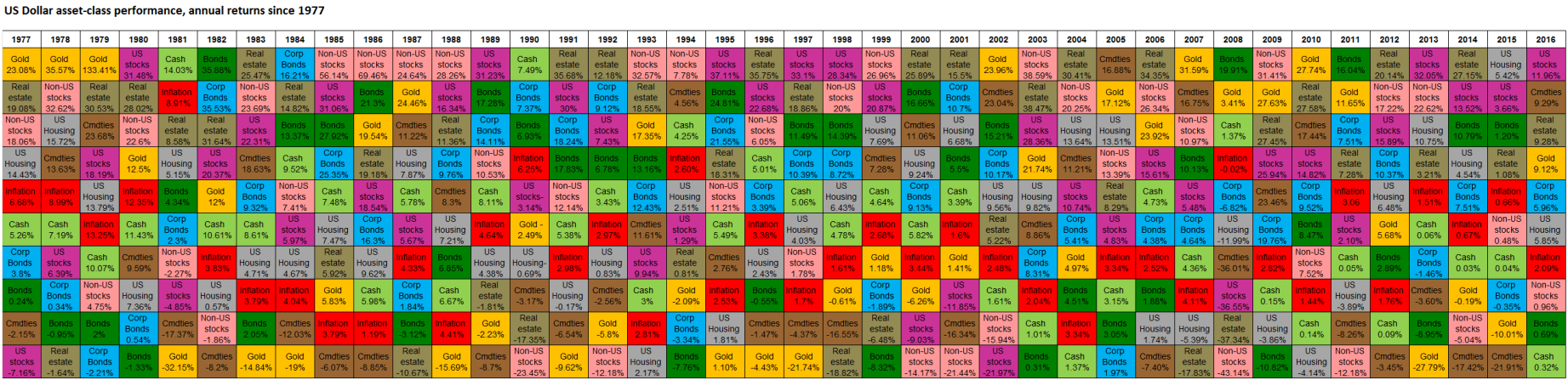
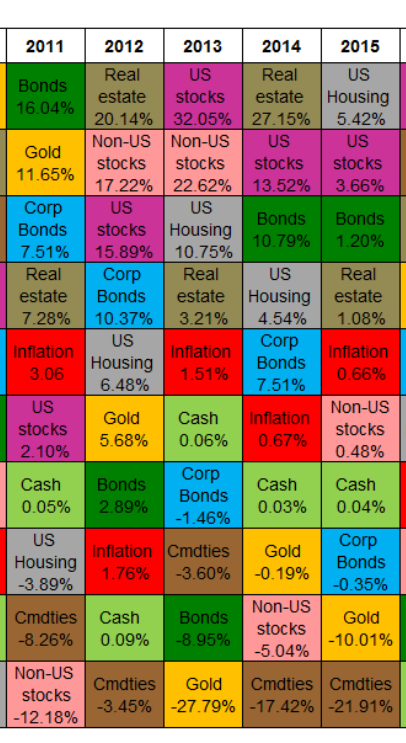
Let's classify investments quite coarsely. One can always apply the same approach to a larger list of investment options.
For each investment, we note the yearly return for every year since 1977 (data from bullionvault.com)
We normalize with respect to inflation, and we compute the growth over 1 year, 3 years, 5 years, 10 years, 20 years.




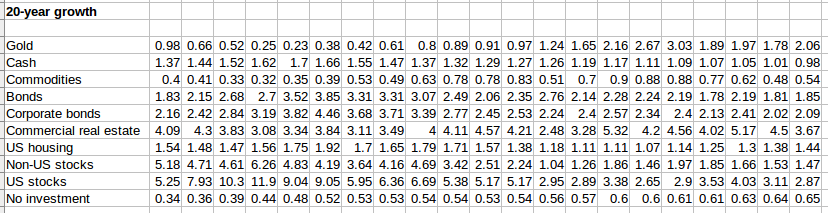
So far, so good.
Now we compute what is the mixture of investments that gives the best risk-free investment growth, assuming that the market can "replay" any past history since 1977, or even mix-and-match different periods of the past.
For those that like math,
this amounts to solving a Linear Program:
Example: 3-year investment
Gold 16.6 %
Cash 46.6 %
Commodities 0.0 %
Bonds 1.3 %
Corporate bonds 8.1 %
Commercial real estate 10.8 %
US housing 0.0 %
Non-US stocks 0.0 %
US stocks 16.6 %
No investment 0.0 %
Risk-free yearly growth 0.9 %
Min yearly growth 0.9 %
Ave yearly growth 4.0 %
Max yearly growth 8.4 %
Risk-free = for any 3-year period in the last 40 years
"Average" means very little: it's the average yearly growth of this mixture of investments in the last 40 years
10 years
Gold 34.4 %
Cash 0.0 %
Commodities 0.0 %
Bonds 16.7 %
Corporate bonds 0.0 %
Commercial real estate 15.9 %
US housing 0.0 %
Non-US stocks 0.0 %
US stocks 32.9 %
No investment 0.0 %
Risk-free yearly growth 4.2 %
Ave yearly growth 6.2 %
Max yearly growth 9.2 %
20 years
Gold 0.0 %
Cash 0.0 %
Commodities 0.0 %
Bonds 0.0 %
Corporate bonds 0.0 %
Commercial real estate 14.8 %
US housing 0.0 %
Non-US stocks 0.0 %
US stocks 85.2 %
No investment 0.0 %
Risk-free yearly growth 5.4 %
Ave yearly growth 8.7 %
Max yearly growth 12.5 %
Many disclaimers
-
This is just an exercise: one could have hundreds of investment options and still apply the method.
-
You typically cannot mix the way you want. Maybe 30% is already invested in a house, and 10% needs to stay uninvested. You can still apply the method, for example for 10-years, and you would get a risk-free return of 2.7% (instead of 4.2%) with the mixture
Gold 26.6 %
US housing 30.0 %
US stocks 33.4 %
No investment 10.0 %
- You are ignoring a lot of information here. For example, you can predict a bit the inflation in the next few years. But the point is that we don't want to do predictions. We want a risk-free investment.
- Don't quote me on the "risk-free". By "risk-free" I mean what I said before in the explanation.