Fast scenario-based decision making
in unbalanced distribution networks

Saverio Bolognani, Florian Dörfler

Automatic Control Laboratory

Future power distribution grids

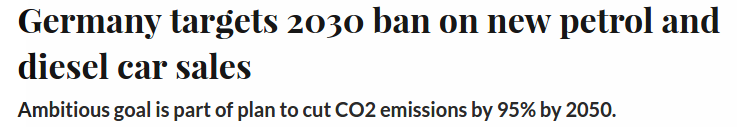
From fit-and-forget to

active power distribution networks

  • Worst case analysis at planning stage
    (e.g. California "15% rule")
  • A little bit of sensing and actuation
  • Real time control

Distribution Network operation under uncertainty

Exogeneous inputs

  • Power generation
  • Power demands
  • Substation voltage

Grid

state

x_\text{exo}
xexox_\text{exo}
x
xx

Control inputs

  • Tap changer
  • Volt/VAR control
  • Voltage regulators
  • Active power control
  • Load shedding
  • Generation curtailment
x_\text{control}
xcontrolx_\text{control}
x \in \mathcal X
x∈Xx \in \mathcal X

Operational constraints

  • Over/under voltage limits
  • Line current limits
  • Transformer loading
  • Voltage stability

Distribution network model

Grid state (nodal variables)

x = (v,\theta, p, q)
x=(v,θ,p,q)x = (v,\theta, p, q)
v_i = \begin{bmatrix} v_i^a \\ v_i^b \\ v_i^c \end{bmatrix}, \quad i = 1, \ldots, N
vi=[viavibvic],i=1,…,Nv_i = \begin{bmatrix} v_i^a \\ v_i^b \\ v_i^c \end{bmatrix}, \quad i = 1, \ldots, N

Power flow equations

v_h e^{j\theta_h} \sum_k \bar{Y}_{hk} v_k e^{-j\theta_k}- p_h - j q_h = 0 \quad \forall h
vhejθh∑kY¯hkvke−jθk−ph−jqh=0∀hv_h e^{j\theta_h} \sum_k \bar{Y}_{hk} v_k e^{-j\theta_k}- p_h - j q_h = 0 \quad \forall h
G(x) = 0
G(x)=0G(x) = 0

Implicit nonlinear model

Uncertain and control inputs

x_\text{exo} = d
xexo=dx_\text{exo} = d

Exogenous stochastic inputs

x_\text{control} = c
xcontrol=cx_\text{control} = c

Control inputs available to the DNO

x_\text{exo} = \begin{bmatrix} \cdots & p_i & q_i & \cdots \end{bmatrix}
xexo=[⋯piqi⋯]x_\text{exo} = \begin{bmatrix} \cdots & p_i & q_i & \cdots \end{bmatrix}

e.g. load

i
ii
x_\text{control} = \begin{bmatrix} \cdots & p_k & q_k & \cdots \end{bmatrix}
xcontrol=[⋯pkqk⋯]x_\text{control} = \begin{bmatrix} \cdots & p_k & q_k & \cdots \end{bmatrix}

e.g. microgenerator

k
kk
V x \le w
Vx≤wV x \le w

Operational constraints

  • Nodal constraints​ (under- / over- voltage, power limits)

  • Proxy for line capacity, transformer current limits, etc.

Chance constrained decision problem

\min \ \ \ J(c)
min   J(c)\min \ \ \ J(c)
\text{subject to}\quad\text{Prob}_d\left[ Vx \le w\right] > 1 - \epsilon
subject toProbd[Vx≤w]>1−ϵ\text{subject to}\quad\text{Prob}_d\left[ Vx \le w\right] > 1 - \epsilon

Complexity of the problem: feasible region.

 

 

An analytical derivation of the feasible region is hopeless

  • general probability distribution for      
  • nonlinear dependence of       on       and         
\mathcal F = \left\{ c \,|\, \text{Prob}_d\left[ Vx \le w\right] > 1-\epsilon \right\}
F={c∣Probd[Vx≤w]>1−ϵ}\mathcal F = \left\{ c \,|\, \text{Prob}_d\left[ Vx \le w\right] > 1-\epsilon \right\}
d
dd
c
cc
x
xx
d
dd

Cost of control

Probability of satisfying constraints

\left\{ \begin{matrix} G(x) = 0\\x_\text{exo} = d\\x_\text{control}=c \end{matrix} \right.
{G(x)=0xexo=dxcontrol=c\left\{ \begin{matrix} G(x) = 0\\x_\text{exo} = d\\x_\text{control}=c \end{matrix} \right.

Nonlinear model

Chance constraints in Power Systems

L. Roald, M. Vrakopoulou, F. Oldewurtel, G. Andersson (2014)
"Risk-Constrained Optimal Power Flow with Probabilistic Guarantees"

D. Bienstock, M. Chertkov, S. Harnett (2014)
"Chance-Constrained OPF: Risk-Aware Network Control under Uncertainty"

T. Summers, J. Warrington, M. Morari, J. Lygeros (2014)
"Stochastic OPF based on convex approximations of chance constraints"

M. Vrakopoulou, M. Katsampani, K. Margellos, J. Lygeros, G. Andersson (2013)
"Probabilistic security-constrained AC optimal power flow"

DC model /
power balance eqs.

Planning /
day ahead dispatch

N-1 criterion
replacement

Scenario approach

Approximate the constraint

 

 

via the set of constraints

 

 

where          are samples (realizations) of 

  • Based on stochastic models (fitted to the data)
  • Directly from the history of the system
\text{Prob}_d\left[ Vx(c,d) \le w\right] > 1-\epsilon
Probd[Vx(c,d)≤w]>1−ϵ\text{Prob}_d\left[ Vx(c,d) \le w\right] > 1-\epsilon
Vx(c,d^{(i)}) \le w \qquad \forall d^{(i)}, i = 1,\ldots, M(\epsilon)
Vx(c,d(i))≤w∀d(i),i=1,…,M(ϵ)Vx(c,d^{(i)}) \le w \qquad \forall d^{(i)}, i = 1,\ldots, M(\epsilon)
d^{(i)}
d(i)d^{(i)}
d.
d.d.

G.C. Calafiore, M.C. Campi (2006)
"The scenario approach to robust control design"

Scenario approach

How many?

\sum_{i=0}^{n_c-1} {{M(\epsilon)}\choose{i}} \epsilon^i (1-\epsilon)^{M(\epsilon)-i} \le \beta
∑i=0nc−1(M(ϵ)i)ϵi(1−ϵ)M(ϵ)−i≤β\sum_{i=0}^{n_c-1} {{M(\epsilon)}\choose{i}} \epsilon^i (1-\epsilon)^{M(\epsilon)-i} \le \beta
\begin{matrix} \epsilon & M(\epsilon) \\ 0.1 & 143 \\ 0.05 & 291 \\ 0.01 & 1475 \end{matrix}
ϵM(ϵ)0.11430.052910.011475\begin{matrix} \epsilon & M(\epsilon) \\ 0.1 & 143 \\ 0.05 & 291 \\ 0.01 & 1475 \end{matrix}
\beta = 10^{-3}, \quad n_c = 5
β=10−3,nc=5\beta = 10^{-3}, \quad n_c = 5
  • Does not depend on the grid size
  • Depends on the number of controls

Computational complexity

For each sample, compute

 

 

and then derive the approximate feasible region

\mathcal F^{(i)} = \left\{ c \,|\, Vx(c,d^{(i)}) \le w \right\}
F(i)={c∣Vx(c,d(i))≤w}\mathcal F^{(i)} = \left\{ c \,|\, Vx(c,d^{(i)}) \le w \right\}
\hat {\mathcal F} = \bigcap_{i} \mathcal F^{(i)}
F^=⋂iF(i)\hat {\mathcal F} = \bigcap_{i} \mathcal F^{(i)}

Computing each feasible region based on NL grid eqs.

is a computationally very intensive task

K. Dvijotham, K. Turitsyn (2015)
"Construction of power flow feasibility sets"

Linear manifold approximant

G(x) = 0
G(x)=0G(x) = 0

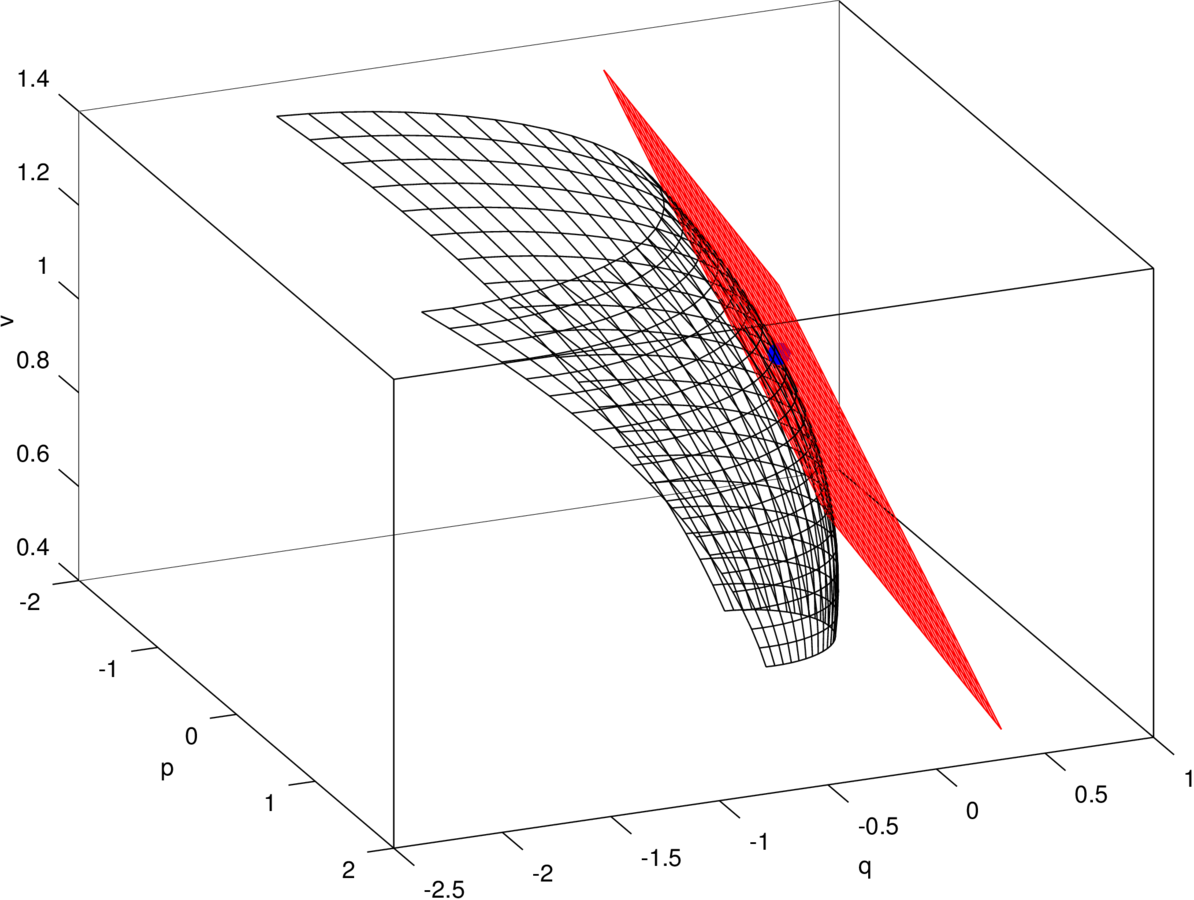
Power flow manifold

x^* \ |\ G(x^*) = 0
x∗ ∣ G(x∗)=0x^* \ |\ G(x^*) = 0

Nominal state

S. Bolognani and F. Dörfler (2015)
“Fast power system analysis via implicit linearization of the power flow manifold”

\nabla G(x^*) ^T (x- x^*) = 0
∇G(x∗)T(x−x∗)=0\nabla G(x^*) ^T (x- x^*) = 0

Tangent space

A_{x^*} x = b_{x^*}
Ax∗x=bx∗A_{x^*} x = b_{x^*}

Under-determined

system of linear equations

Linear manifold approximant

  • Sparse
  • Structure preserving
  • No assumption on
    • X/R ratio
    • constant voltage
    • radial network
  • Implicit linear relation

Compare with DC, LinDistFlow, ...

\left\{ \begin{matrix} G(x) = 0\\x_\text{exo} = d\\x_\text{control}=c \end{matrix} \right.
{G(x)=0xexo=dxcontrol=c\left\{ \begin{matrix} G(x) = 0\\x_\text{exo} = d\\x_\text{control}=c \end{matrix} \right.
\left\{ \begin{matrix} Ax = b\\x_\text{exo} = d\\x_\text{control}=c \end{matrix} \right.
{Ax=bxexo=dxcontrol=c\left\{ \begin{matrix} Ax = b\\x_\text{exo} = d\\x_\text{control}=c \end{matrix} \right.

Sparse implicit linear model

Implicit nonlinear model

Linear manifold approximant

General case

Extended state

\tilde x = (v,\theta,\text{Re}(i), \text{Im}(i),p,q)
x~=(v,θ,Re(i),Im(i),p,q)\tilde x = (v,\theta,\text{Re}(i), \text{Im}(i),p,q)
\tilde G(x) = \left[ \begin{matrix} \tilde G^\text{edges}(\tilde x)\\ \tilde G^\text{nodes}(\tilde x) \end{matrix} \right]
G~(x)=[G~edges(x~)G~nodes(x~)]\tilde G(x) = \left[ \begin{matrix} \tilde G^\text{edges}(\tilde x)\\ \tilde G^\text{nodes}(\tilde x) \end{matrix} \right]
\tilde G^\text{edges}(x) = Yu - i
G~edges(x)=Yu−i\tilde G^\text{edges}(x) = Yu - i
\tilde G_h^\text{nodes}(x) = u_h \bar i_h - s_h
G~hnodes(x)=uhi¯h−sh\tilde G_h^\text{nodes}(x) = u_h \bar i_h - s_h
u_h := v_h e^{j\theta_h}
uh:=vhejθhu_h := v_h e^{j\theta_h}

From complex-value to real-valued equations

f(x) = Ax
f(x)=Axf(x) = Ax
\frac{\partial f}{\partial x} = \langle A \rangle, \quad \langle A \rangle := \begin{bmatrix} \text{Re}A & -\text{Im}A \\ \text{Im}A & \text{Re}A \end{bmatrix}
∂f∂x=⟨A⟩,⟨A⟩:=[ReA−ImAImAReA]\frac{\partial f}{\partial x} = \langle A \rangle, \quad \langle A \rangle := \begin{bmatrix} \text{Re}A & -\text{Im}A \\ \text{Im}A & \text{Re}A \end{bmatrix}

complex-valued

real-valued

\langle \bar A \rangle = N \langle A \rangle N, \quad N := \begin{bmatrix} I & 0 \\ 0 & -I \end{bmatrix}
⟨A¯⟩=N⟨A⟩N,N:=[I00−I]\langle \bar A \rangle = N \langle A \rangle N, \quad N := \begin{bmatrix} I & 0 \\ 0 & -I \end{bmatrix}

Linear manifold approximant

\frac{\partial \begin{bmatrix} \text{Re}(u) \\ \text{Im}(u) \end{bmatrix} }{ \partial \begin{bmatrix} v \\ \theta \end{bmatrix} } = P(v,\theta) := \begin{bmatrix} \text{diag}(\cos\theta) & -\text{diag}(v) \text{diag}(\sin\theta) \\ \text{diag}(\sin\theta) & \text{diag}(v) \text{diag}(\cos\theta) \end{bmatrix}
∂[Re(u)Im(u)]∂[vθ]=P(v,θ):=[diag(cosθ)−diag(v)diag(sinθ)diag(sinθ)diag(v)diag(cosθ)]\frac{\partial \begin{bmatrix} \text{Re}(u) \\ \text{Im}(u) \end{bmatrix} }{ \partial \begin{bmatrix} v \\ \theta \end{bmatrix} } = P(v,\theta) := \begin{bmatrix} \text{diag}(\cos\theta) & -\text{diag}(v) \text{diag}(\sin\theta) \\ \text{diag}(\sin\theta) & \text{diag}(v) \text{diag}(\cos\theta) \end{bmatrix}

Evaluate the partial derivatives of

\tilde G(\tilde x)
G~(x~)\tilde G(\tilde x)
\left. \frac{\partial \tilde G}{\partial \tilde x} \right|_{\tilde x^*} = \begin{bmatrix} \langle Y \rangle P(v^*,\theta^*) & -I & 0 \\ N \langle \text{diag } i^* \rangle N P(v^*,\theta^*) & \langle \text{diag } v^* \rangle N & -I \end{bmatrix}
∂G~∂x~∣x~∗=[⟨Y⟩P(v∗,θ∗)−I0N⟨diag i∗⟩NP(v∗,θ∗)⟨diag v∗⟩N−I]\left. \frac{\partial \tilde G}{\partial \tilde x} \right|_{\tilde x^*} = \begin{bmatrix} \langle Y \rangle P(v^*,\theta^*) & -I & 0 \\ N \langle \text{diag } i^* \rangle N P(v^*,\theta^*) & \langle \text{diag } v^* \rangle N & -I \end{bmatrix}
\nabla G^T(x^*) = \begin{bmatrix} \Big( N \langle \text{diag } i^* \rangle N + \langle \text{diag } v^* \rangle N \langle Y \rangle \Big) P(v^*,\theta^*) & -I \end{bmatrix}
∇GT(x∗)=[(N⟨diag i∗⟩N+⟨diag v∗⟩N⟨Y⟩)P(v∗,θ∗)−I]\nabla G^T(x^*) = \begin{bmatrix} \Big( N \langle \text{diag } i^* \rangle N + \langle \text{diag } v^* \rangle N \langle Y \rangle \Big) P(v^*,\theta^*) & -I \end{bmatrix}

Eliminate currents and obtain

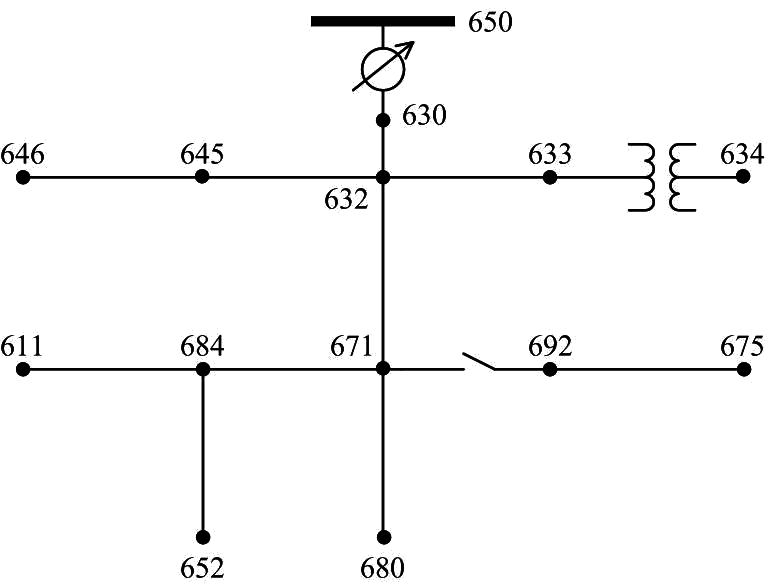
IEEE 13 Test feeder

  • Relatively highly loaded
  • Substation voltage regulator
  • Overhead and underground lines
  • Variety of phasing
  • Shunt capacitor banks
  • Unbalanced loads

Quality of the approximation

Approximate feasible region

\mathcal F^{(i)} = \left\{ c \,|\, Vx(c,d^{(i)}) \le w \right\}
F(i)={c∣Vx(c,d(i))≤w}\mathcal F^{(i)} = \left\{ c \,|\, Vx(c,d^{(i)}) \le w \right\}
\hat{\mathcal F}^{(i)} = \text{Proj}_c \hat{\mathcal F}_x^{(i)}
F^(i)=ProjcF^x(i)\hat{\mathcal F}^{(i)} = \text{Proj}_c \hat{\mathcal F}_x^{(i)}
\hat{\mathcal{F}}_x^{(i)} = \left\{ x \,|\, \begin{matrix} Ax = b \\ x_\text{exo} = d^{(i)} \\ Vx \le w \end{matrix} \right\}
F^x(i)={x∣Ax=bxexo=d(i)Vx≤w}\hat{\mathcal{F}}_x^{(i)} = \left\{ x \,|\, \begin{matrix} Ax = b \\ x_\text{exo} = d^{(i)} \\ Vx \le w \end{matrix} \right\}

Feasible
control inputs

i-th feasible region for the scenario approach

Feasible
states

Approximate feasible region

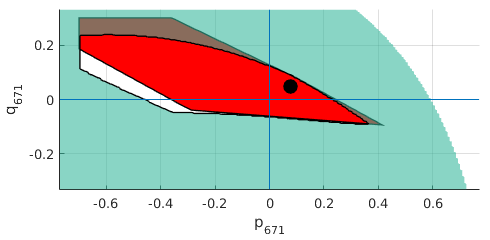
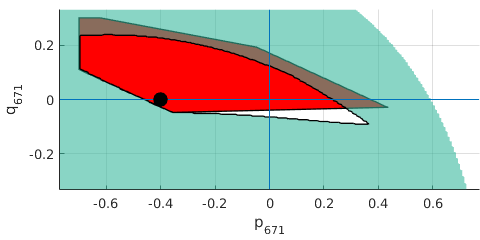
Linearization point matters!

  • Zero-load profile
  • Numerical solution in typical conditions
  • Measured state

Polytope operations

\hat F^{(i)} = \text{Proj}_c \hat F_x^{(i)}
F^(i)=ProjcF^x(i)\hat F^{(i)} = \text{Proj}_c \hat F_x^{(i)}
\hat F_x^{(i)} = \left\{ x \,|\, \begin{matrix} Ax = b \\ x_\text{exo} = d^{(i)} \\ Vx \le w \end{matrix} \right\}
F^x(i)={x∣Ax=bxexo=d(i)Vx≤w}\hat F_x^{(i)} = \left\{ x \,|\, \begin{matrix} Ax = b \\ x_\text{exo} = d^{(i)} \\ Vx \le w \end{matrix} \right\}
\hat F = \bigcap_i \hat F^{(i)}
F^=⋂iF^(i)\hat F = \bigcap_i \hat F^{(i)}
  • Convenient representation for optimization
    • ​Linear inequalities in reduced dimension
  • Many redundant constraints
    • ​Fourier-Motzkin elimination
  • Fast operations on polytopes
i = 1,\ldots, N
i=1,…,Ni = 1,\ldots, N
i = 1,\ldots, N
i=1,…,Ni = 1,\ldots, N

Chance-constrained feasible region

Disturbances

  • Power demand of spot loads

Operational constraints

  • Under- and over-voltage limits

Decision variables

  • Generation curtailment @671
  • Tap changer position @630

5% confidence

M(\epsilon) = 181
M(ϵ)=181M(\epsilon) = 181
\epsilon = 0.05
ϵ=0.05\epsilon = 0.05

Microgenerator

Tap changer

Simulations

MultiParametric Toolbox for Matlab by IfA

  • Towards real time chance-constrained operation
  • Next step: 
    • Slow data - Forecast of uncertain inputs (offline)
    • Fast data - Real time measurements (online)

Saverio Bolognani

bsaverio@ethz.ch

http://control.ee.ethz.ch/~bsaverio

Thank you for your attention.