Identifying Latent Intentions
via
Inverse Reinforcement Learning
in
Repeated Public Good Games
Carina I Hausladen, Marcel H Schubert, Christoph Engel



MAX PLANCK INSTITUTE
FOR RESEARCH ON COLLECTIVE GOODS
- Social Dilemma Games
-
Initial contributions start positive but gradually decline over time.
-
-
Classify behavior to understand contribution patterns
- Fischbacher et al. (2001) via Selten (1967)'s Strategy Method
Meta-Analysis
Thöni et al. (2018)
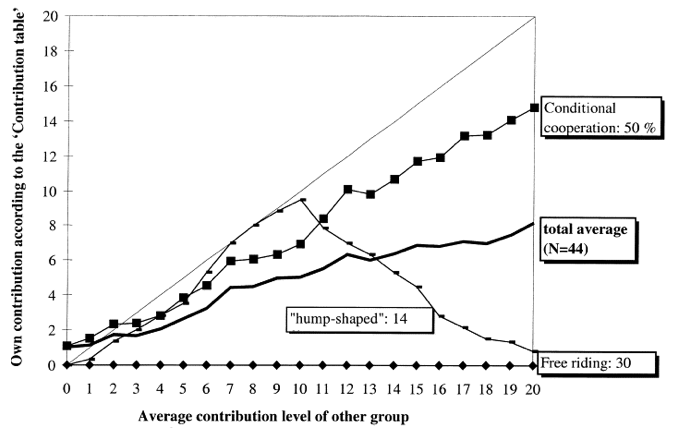
Conditional Cooperation
19.2 %
Hump-Shaped
Fischbacher et al. (2001)
61.3 %
Freeriding
10.4 %

Meta-Analysis
Thöni et al. (2018)
Conditional Cooperation
19.2 %
Hump-Shaped
Fischbacher et al. (2001)
61.3 %
Freeriding
10.4 %
Strategy Method Data
Game Play Data
Analysing Game Play Data
- Finite Mixture Model
- Bayesian Model
-
C-Lasso
-
Clustering
Theory Driven
Data Driven
- Assumes Four Types
- Estimates type probabilities and behavioral parameters via EM.
- Functional form: Decision depends on past choices, payoffs, and group behavior.
- Classifies individuals and estimates parameters simultaneously.
- Penalizes differences to reveal latent behavioral groups.
- Functional Form: Based on past choices, payoffs, and future value.
- Estimation: Bayesian mixture model
- Clustering: Gibbs sampling assigns behavioral types.
- Pattern recognition: Own & co-player decisions
- Manhattan Distance + Hierarchical clustering
Analysing Game Play Data
- Finite Mixture Model
- Bayesian Model
-
C-Lasso
-
Clustering
Theory Driven
Data Driven
Theory first: Use theory to find groups
Model first:
Specify a model, then find groups
Data first: Let the data decide groups, then theorize
Behavior Beyond Theory
- Finite Mixture Model
- Bayesian Model
-
C-Lasso
-
Clustering
Theory Driven
Data Driven
Bardsely (2006)| Tremble terms: 18.5%.
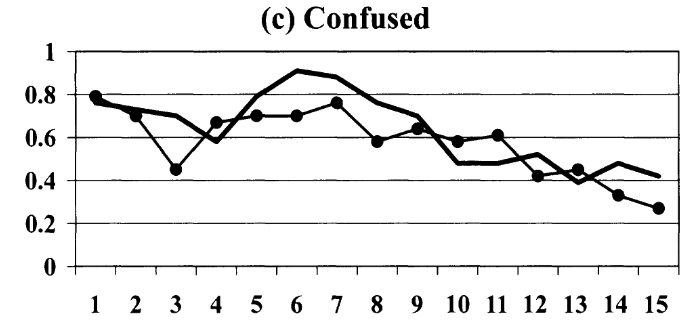
Houser (2004) | Confused: 24%
Fallucchi (2021) |Others: 22% – 32%
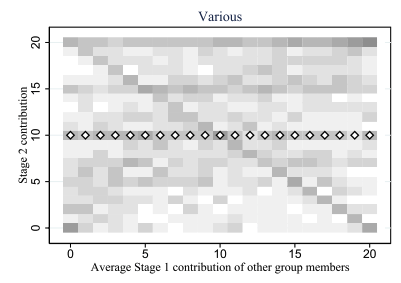
Fallucchi (2019) |Various: 16.5%
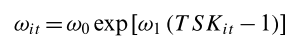
initial tremble
simulated
actual
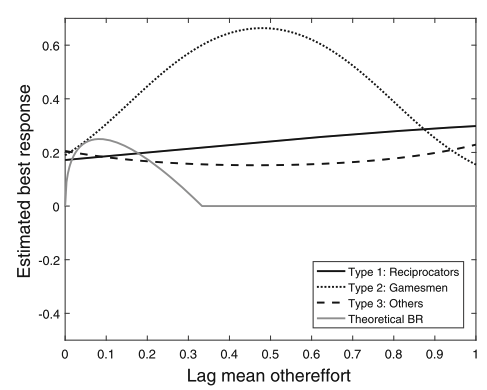
Others
18.5%
24%
32%
16.5%
random / unexplained
Step 1
Clustering
→ uncover patterns
Step 2
Inverse Reinforcement Learning
→ interpret patterns
Can we build a model that explains both
the behavior types we know and the ones we don’t?
Dataset
- Data from 10 published studies
-
2,938 participants,
50,390 observations - Game play data
- Standard linear public good games
- No behavioral interventions
- Identical information treatment
two-dimensional time series
per player
What are the most common patterns in the data?
What are the most common patterns in the data?
Step 1
Clustering
→ uncover patterns
Step 2
Inverse Reinforcement Learning
→ interpret patterns
Clustering consists of three main steps
- Choose the number of clusters k
- Calculate distances between series
- Apply a clustering algorithm to group similar series
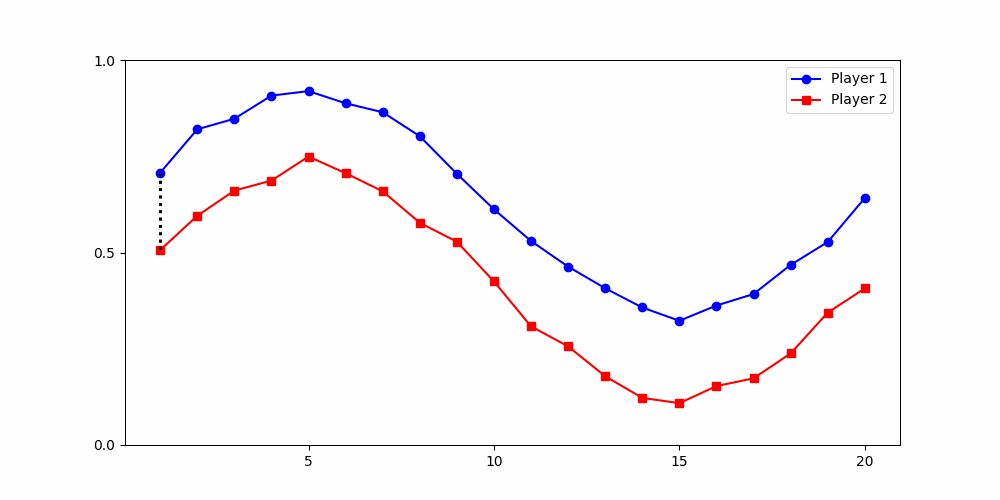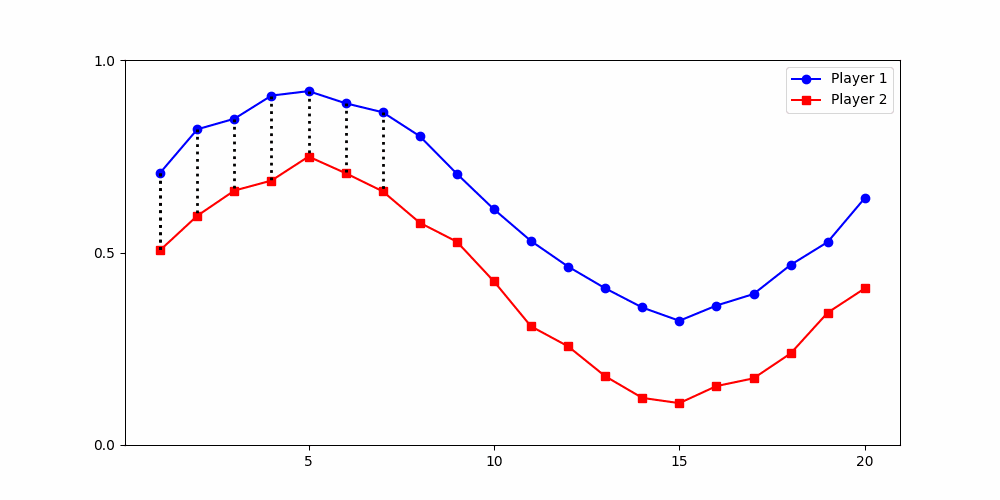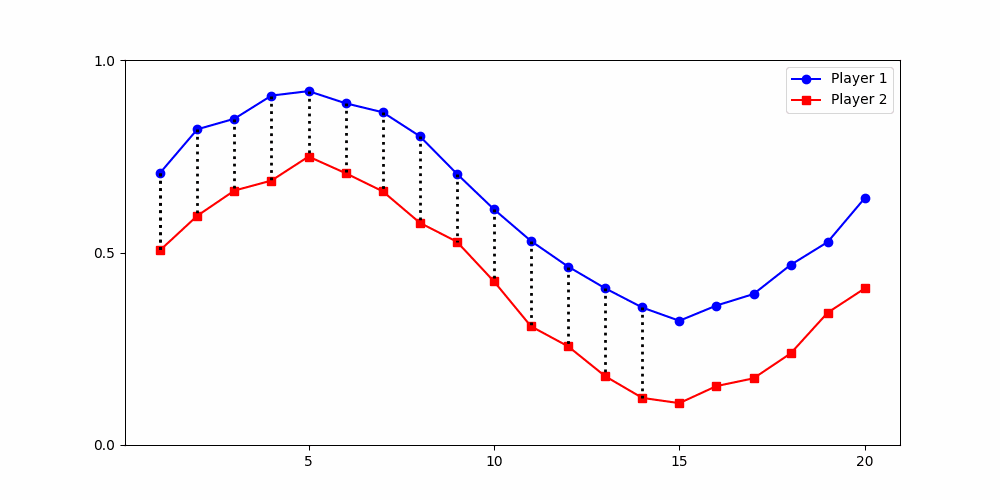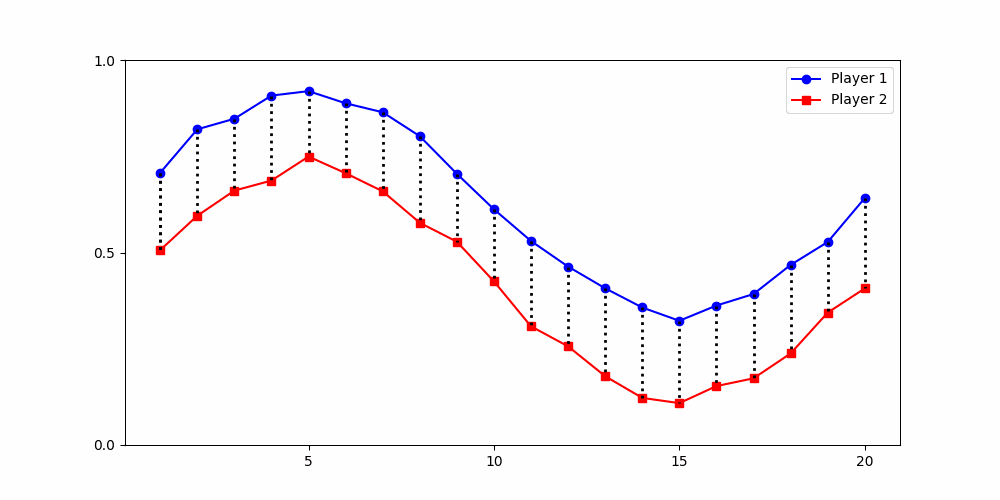
Calculating Distances
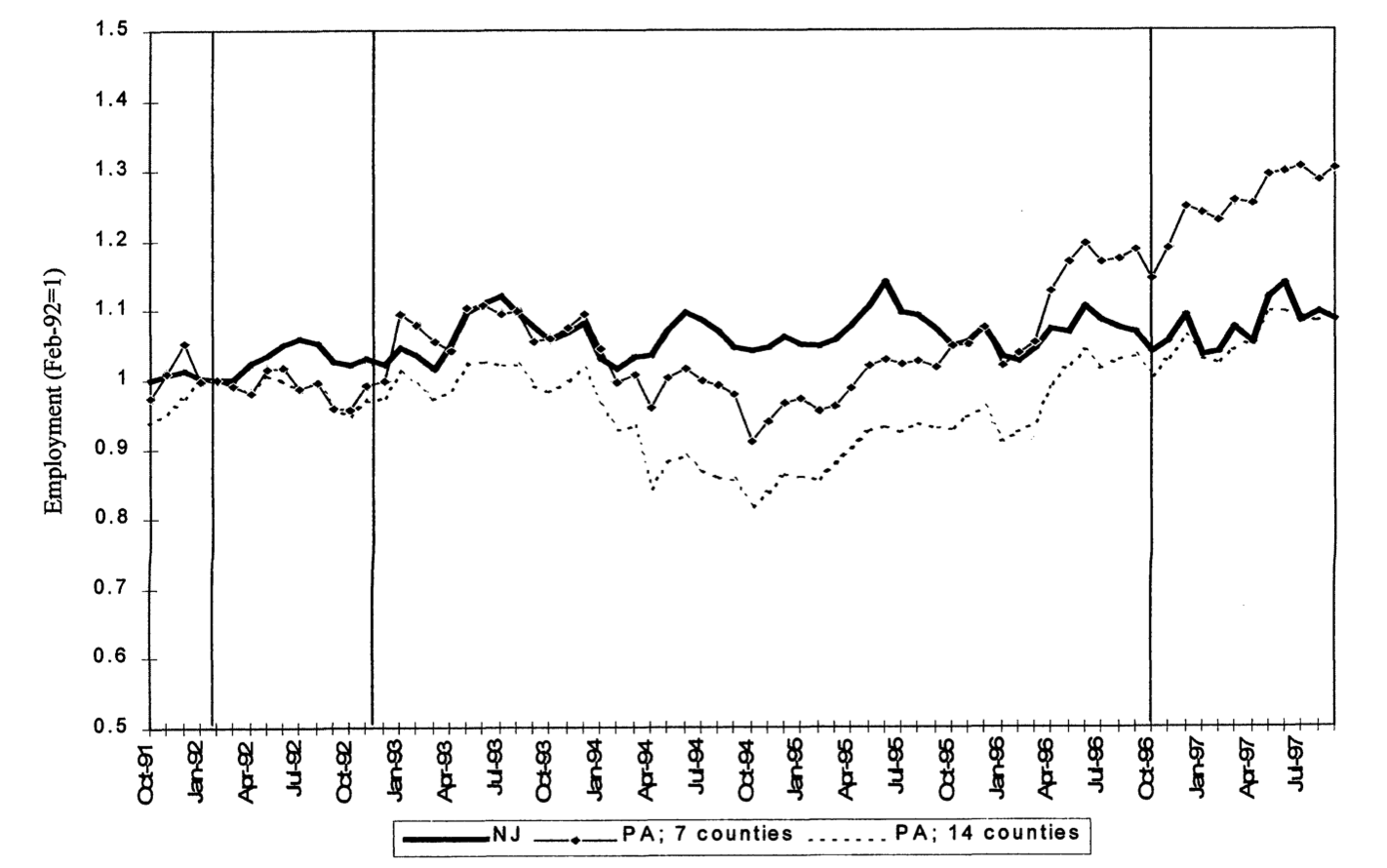
- Minimum wage increase in NJ (April 1992) hit all firms at the same calendar time.
- The policy hit all fastfood companies in NJ at the same time.
Minimum Wages and Employment
Cart & Krueger (2000)
- Round 2 ≠ same experience
- Local time-points are misleading
- Better: compare global shape
rounds
20
contribution
1
0

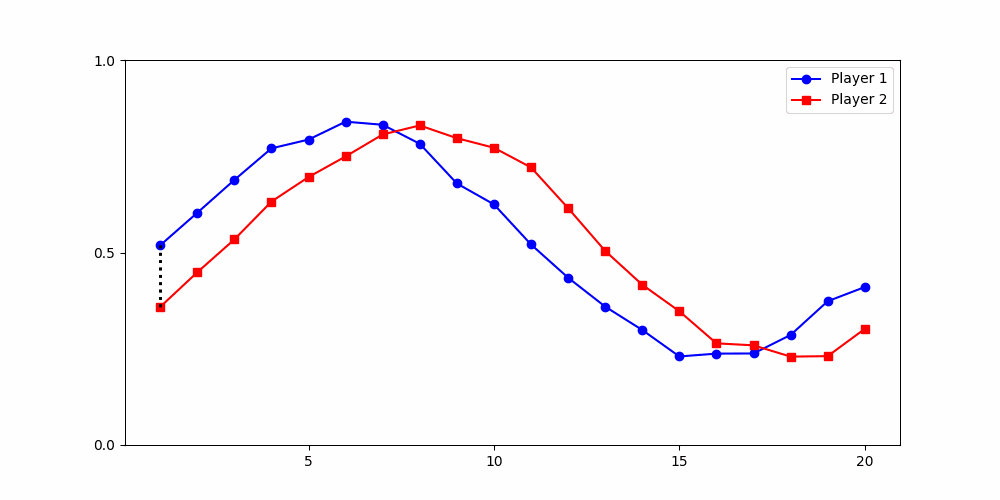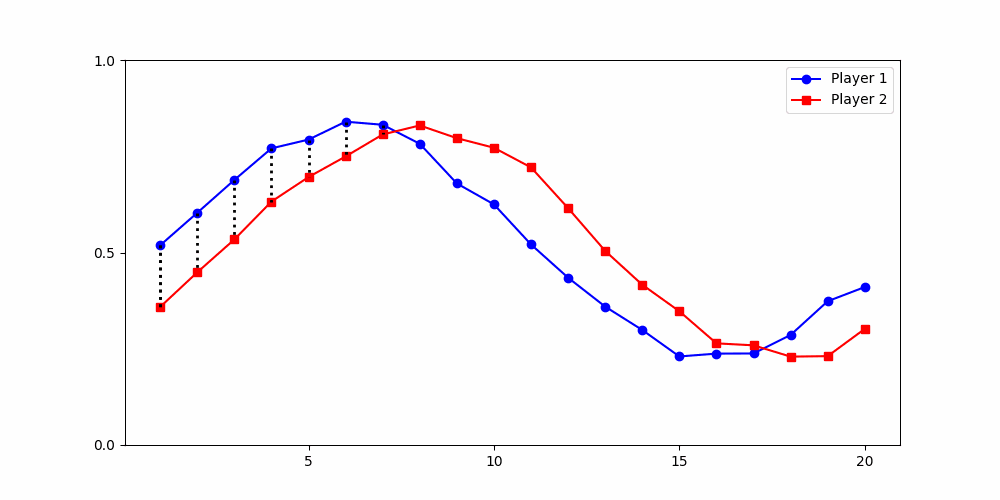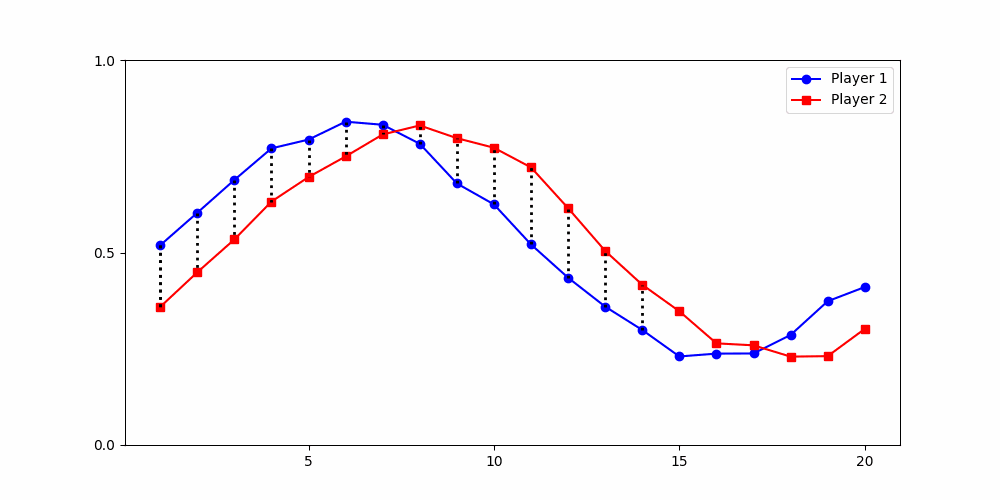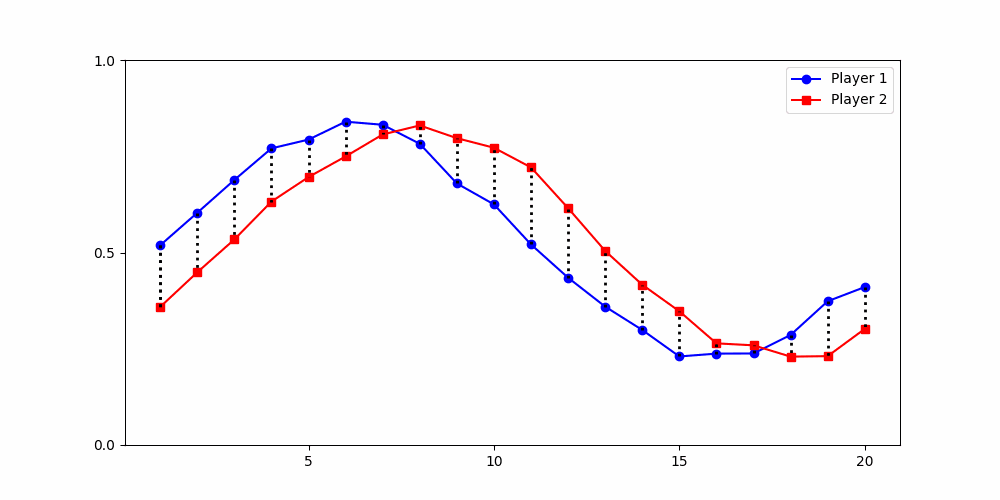

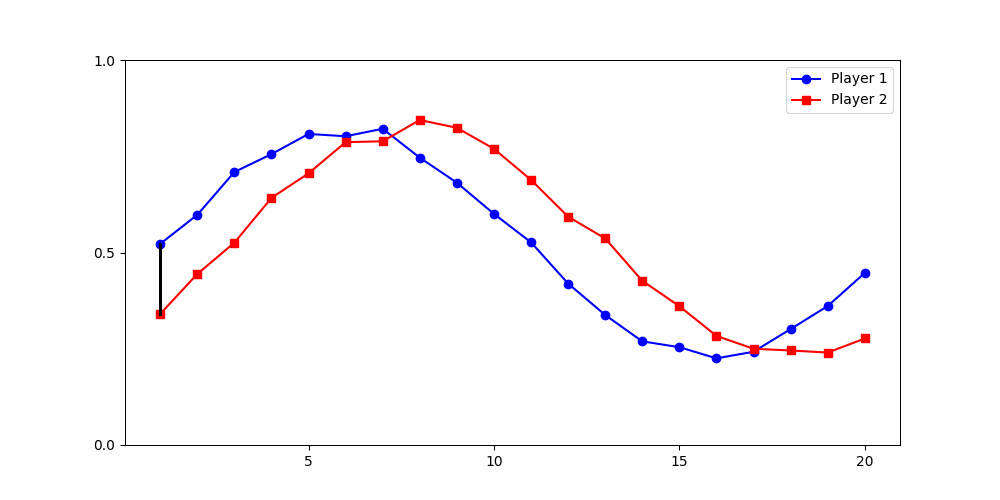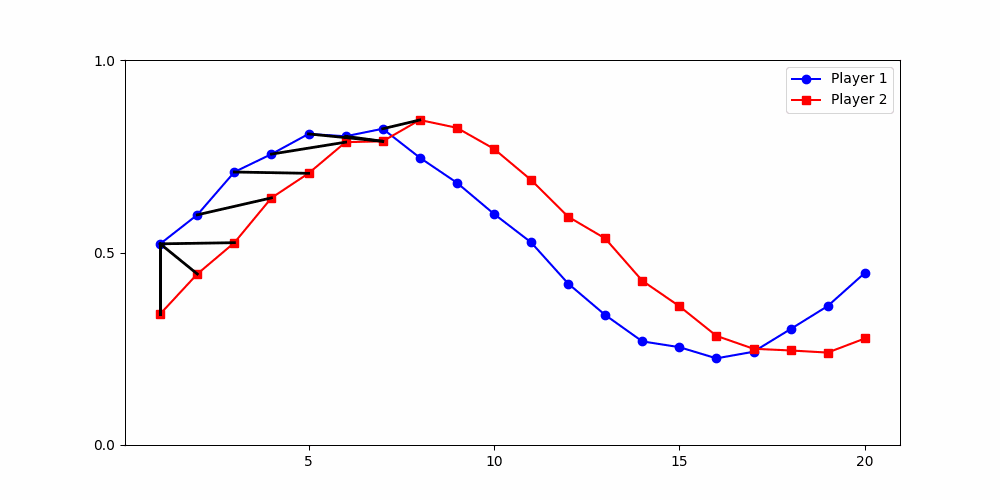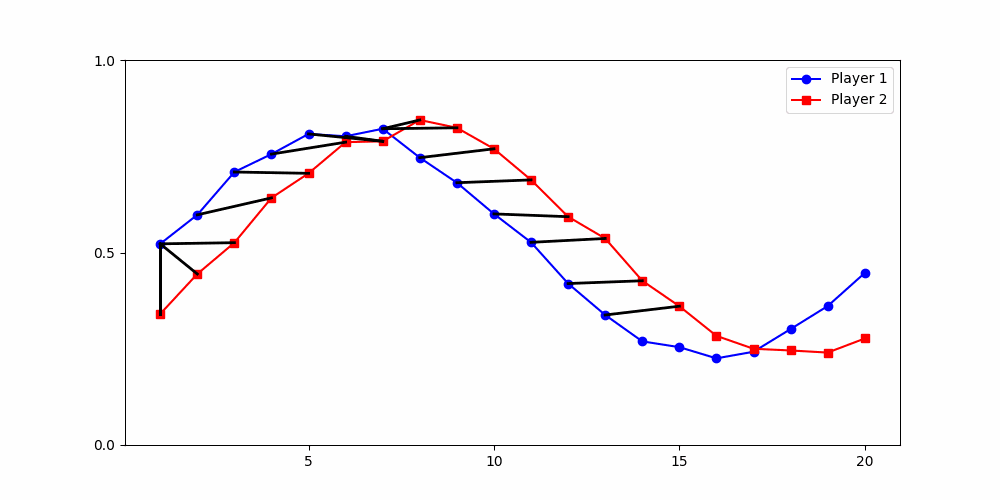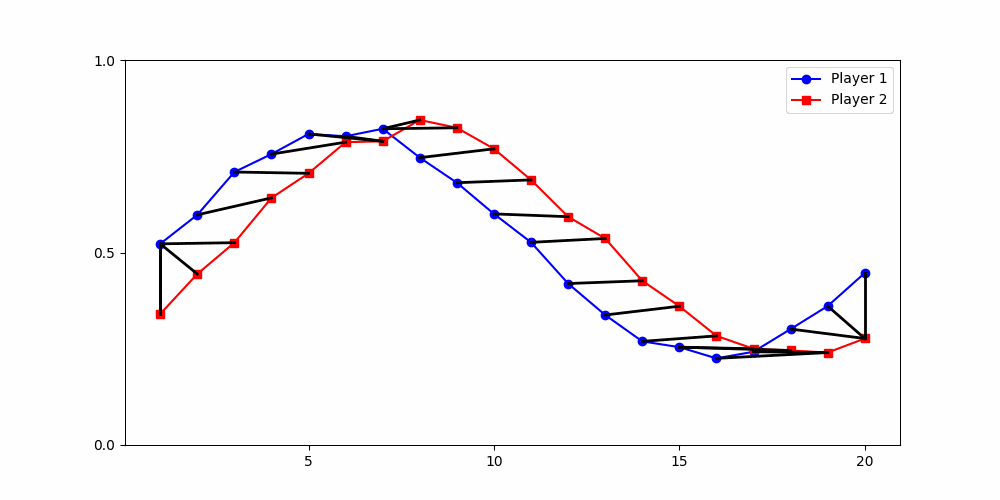


Local Similarity Measure
Global Similarity Measure
Dynamic Time Warping (DTW)
Euclidean Distance
Empirical Perspective
Clustering consists of three main steps
- Choose the number of clusters k
- Calculate distances between series
- Euclidean (local)
- DTW (global)
- Apply a clustering algorithm to group similar series
- k-means clustering
- Gaussian Mixture Models (GMM)
- Agglomerative clustering


Agglom
GMM
k-means
Agglom
GMM
k-means

DTW
Euclidean
k-means
uids
round


global
local
Agglom
GMM
k-means

DTW
Euclidean
k-means

DTW
Euclidean
Contrasting Perspectives
- A local— drop from high to low contributions at different times,
- within a global trend of sustained high then low contributions.
- A shared local switching point,
but clusters stay noisy due to ignored global patterns.



DTW
Euclidean

-
Results depend fundamentally on how similarity is defined.
-
We focus on generalizable patterns.
Our
Clustering Setup
- Choose the number of clusters k
- k = 6
- Calculate distances between series
- DTW distance (global)
- Apply a clustering algorithm to group similar series
- Spectral Clustering
- Choose the number of clusters k
-
-
- Calculate distances between series
- DTW distance (global)
- Apply a clustering algorithm to group similar series
- Spectral Clustering
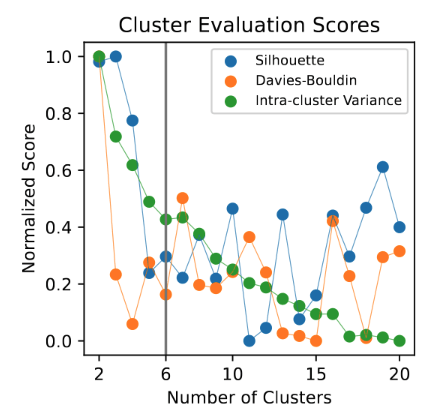
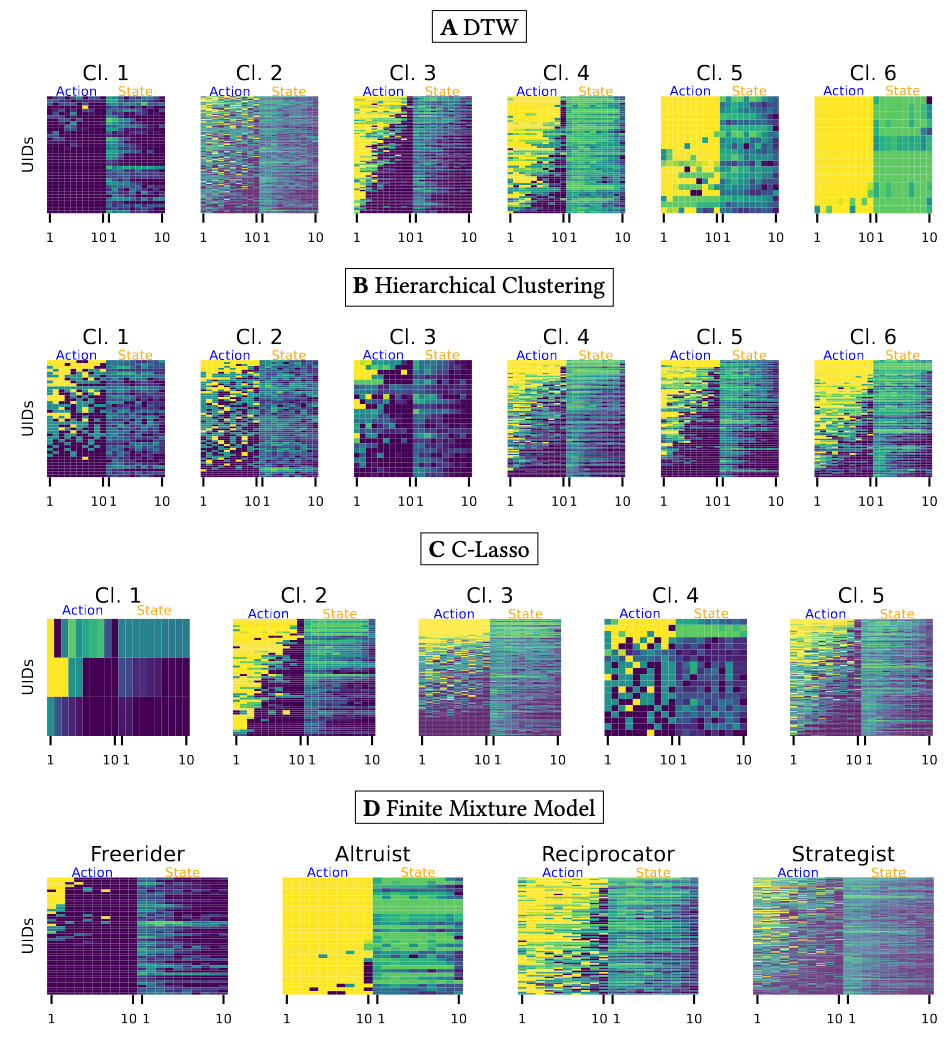
Comparing Partitioning Methods
Theory Driven
Data Driven
Manhattan +
Finite Mixture Model
Bayesian Model
C-Lasso
DTW +
Spectral Clustering
Hierarchical Clustering
Theory Driven
Data Driven
Finite Mixture Model
C-Lasso
DTW Distance
Manhattan Distance




Finite Mixture Model
C-Lasso
DTW
Local
Clustering
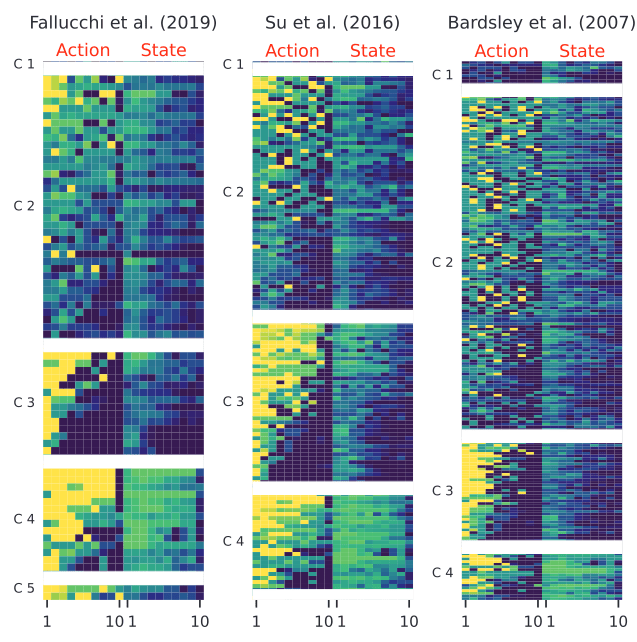
DTW-based clustering leads to a clearer, less noisy partition.
Interpreting the Clusters
Interpreting the Clusters
Step 1
Clustering
→ uncover patterns
Step 2
Inverse Reinforcement Learning
→ interpret patterns
- evolutionary game-theoretic learning
- best-response learning
-
reinforcement learning
-
Q-learning
- prisoner's dilemma (Dolgopolov 2024)
- PGGs (Zheng 2024)
-
Q-learning
Learning in social dilemmas
The key challenge is to define a
Reward Function
inverse
- recovers reward functions from data
- lead to breakthroughs in robotics, autonomous driving, and
modeling animal behavior
Hierarchical Inverse Q-Learning (Zhu 2024)
Hierarchical Inverse Q-Learning
action
state
Markov Decision Process: \( P(s' |s,a) \)

Q-value update:
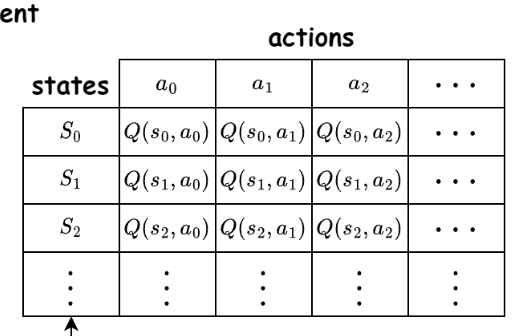
Maintains a Q-table:
\( \epsilon \)-greedy policy:
\( a = \begin{cases} \text{a random action}, & \epsilon \\ \displaystyle \arg\max_a Q(s,a), & 1- \epsilon \end{cases}\)
\( Q_{new}(s,a) = (1- \alpha) Q_{old}(s,a) + \alpha \left( r + \gamma \max Q_{old}(s', a') - Q_{old}(s,a) \right) \)
reward
discount
learning rate
Hierarchical Inverse Q-Learning
action
state

\( Q_{new}(s,a) = (1- \alpha) Q_{old}(s,a) + \alpha \left( r + \gamma \max Q_{old}(s', a') - Q_{old}(s,a) \right) \)
reward
Estimate the reward function by maximizing the likelihood of observed actions and states.
unknown
Hierarchical Inverse Q-Learning
\( r_{t-1} \)
\( a_{t-1} \)
P
\( s \)
\( \Lambda \)
\( r_t \)
\( a_t \)
P
\( s_{t+1} \)
discrete transition
Hierarchical Inverse
Q-Learning
\( P(r_t \mid s_{0:t}, a_{0:t}) \)
action
state

\( r \)
How many reward functions?
How many reward functions should we estimate?
1
2
3
4
→ 2
→ 3
→ 4
→ 5
0.6
0.4
0.2
0.2
75.2
88.6
101.5
114.4
\( \Delta \) Test LL
\( \Delta \) BIC
Choice of two intentions aligns with the fundamental RL principle of exploration vs. exploitation.
Hierarchical Inverse
Q-Learning
\( P(r_t \mid s_{0:t}, a_{0:t}) \)
action
state

\( r \)





Unconditional
Cooperators
Consistent
Cooperators


Freeriders
-
- The intention to free-ride is not fixed.
- Some variation exists, but the competing intention never exceeds the adoption threshold .


Threshold
Switchers


Volatile
Explorers
- The cluster actively experiments with new strategies.
- Deliberate switching between strategies.
Various Game Lengths


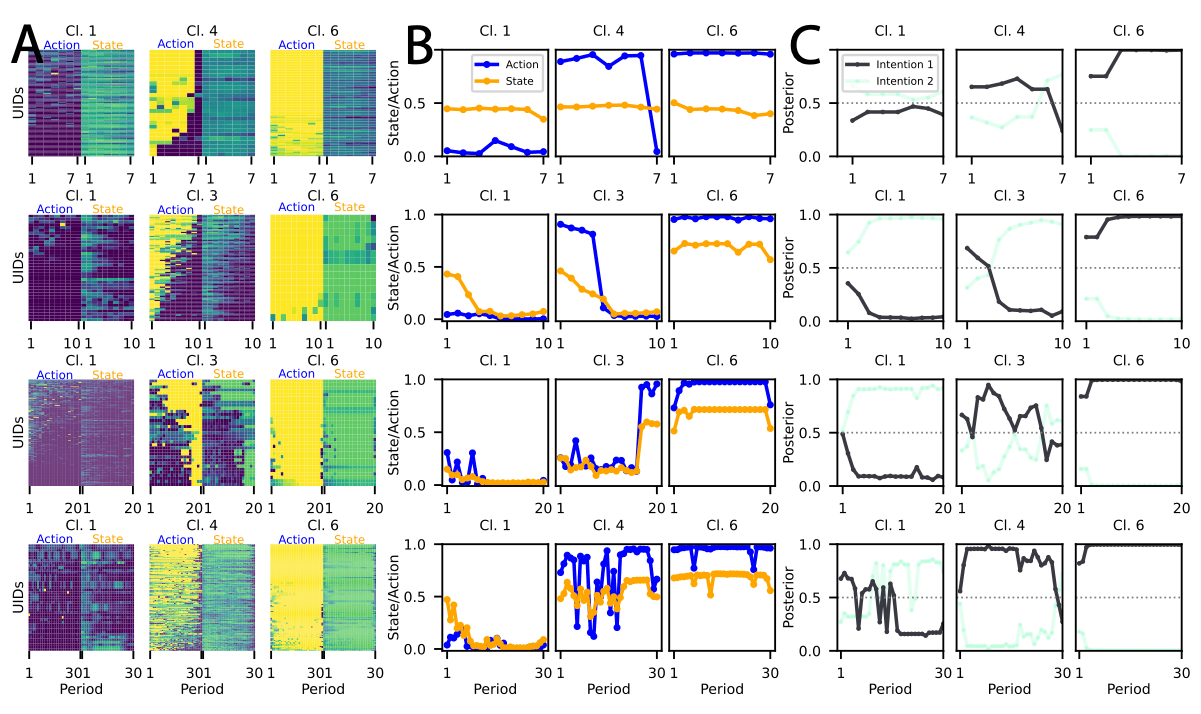

- The intention to free-ride may be less rigid than previously assumed.
- Longer horizons
- increase intention volatility and thus
- create more opportunities for behavioral shifts.
Freeriders

- Longer time horizons generally promote cooperation.
- A small group of participants remains cooperative regardless of game duration.
- For some, cooperation is a stable trait rather than a response to game length.
Consistent Cooperators
Conclusion
Dataset with ~ 50'000 observations from PGG



A global distance metric, such as two-dimensional Dynamic Time Warping (DTW), is best-suited for partitioning data from social dilemma games.
Estimating intentions that transition in a discrete manner offers a unifying theory to explain all behavioral clusters — including the 'Other' cluster.
carinah@ethz.ch
slides.com/carinah
S
Appendix
Hierarchical Inverse Q-Learning
action
state
- Markov Decision Process: \( P(s' |s,a) \)
- Behavior of a Q-learner:
- maintains a Q-table
- exploitation vs. exploration
- Q-value update


\( Q(s,a) = (1- \alpha) Q(s,a) + \alpha \left( r + \gamma \max Q(s', a') - Q(s,a) \right) \)
Expected best possible outcome from the next state
Compare to now
re-ward
Hierarchical Inverse Q-Learning
action
state
Markov Decision Process: \( P(s' |s,a) \)


Expected best possible outcome from the next state
Compare to now
re-ward
Q-value update
Maintains a Q-table
\( \epsilon \)-greedy policy:
\( a = \begin{cases} \text{a random action}, & \epsilon \\ \displaystyle \arg\max_a Q(s,a), & 1- \epsilon \end{cases}\)
\( Q_{new}(s,a) = (1- \alpha) Q_{old}(s,a) + \alpha \left( r + \gamma \max Q_{old}(s', a') - Q_{old}(s,a) \right) \)
