Equivariant normalizing flows and their application to cosmology

Carolina Cuesta-Lazaro

 April 2022 - IAIFI JC

\theta

Simulated Data

Data

Prior

Posterior

x_\mathrm{obs}
x
P(\theta|x_\mathrm{obs})

Forwards

Inverse

\theta = {\Omega_M, \sigma_8}

Cosmological parameters

EARLY UNIVERSE

LATE UNIVERSE

Normalizing flows: Generative models and  density estimators

x
z
x
z

VAE,GAN ...

Gaussianization

Data space

Latent space

x = \green{f_\phi}(z)

Image Credit: https://lilianweng.github.io/posts/2018-10-13-flow-models/

\mathcal{L}(\mathcal{D}) = - \frac{1}{\vert\mathcal{D}\vert}\sum_{\mathbf{x} \in \mathcal{D}} \log p(\mathbf{x})

Maximize the data likelihood

NeuralNet

p(\mathbf{x}) = p_z(\mathbf{z}) \left\vert \det \dfrac{d \mathbf{z}}{d \mathbf{x}} \right\vert = p_z(f^{-1}(\mathbf{x})) \left\vert \det \dfrac{d f^{-1}}{d \mathbf{x}} \right\vert

f must be invertible

J efficient to compute 

1-D

n-D

p(\mathbf{x}) = p_z(f^{-1}(\mathbf{x})) \left\vert \det J(f^{-1}) \right\vert
x = f(z), \, z = f^{-1}(x)
p(\mathbf{x}) = p_z(\mathbf{z}) \left\vert \det \dfrac{d \mathbf{z}}{d \mathbf{x}} \right\vert
p(\mathbf{x}|\theta) = p_z(f^{-1}(\mathbf{x}|\theta)) \left\vert \det J(f^{-1}|\theta) \right\vert

Equivariance

f(\mathcal{G} x) = \mathcal{G} f(x)
\mathcal{G}
\mathcal{G}
f
\mathcal{G}

Invariance

f(\mathcal{G}x) = f(x)
f

Equivariant

p_X(\mathcal{G}\mathbf{x}) = p_Z(f(\mathcal{G}\mathbf{x})) |\det J_f(\mathcal{G}\mathbf{x}))|

Invariant

f
p(x)
= p_Z(\mathcal{G}f(\mathbf{x})) |\det \mathcal{G} J_f(\mathbf{x}))|
= p_Z(f(\mathbf{x})) |\det J_f(\mathbf{x}))|

Equivariant

f

Invariant

p_Z

Challenge: Expressive + Invertible + Equivariant

1. Continuous time Normalizing flows

ODE solutions are invertible!

\mathbf{z} = \mathbf{x} + \int_0^1 \phi(\mathbf{x}(t)) dt
\mathbf{x} = \mathbf{z} + \int_1^0 \phi(\mathbf{x}(t)) dt
z = odeint(self.phi, x, [0, 1])

torchdiffeq

\log p_X(\mathbf{x}) = \log p_Z(\mathbf{z}) + \int_0^1 \mathrm{Tr }\, J _{\phi}(\mathbf{x}(t)) dt

solving the ODE might introduce error in estimating p(x)

Image Credit: https://arxiv.org/abs/1810.01367

\mathbf{x} = \mathbf{z} + \int_1^0 \phi(\mathbf{x}(t)) dt
\mathbf{z} = \mathbf{x} + \int_0^1 \phi(\mathbf{x}(t)) dt

Equivariant? GNNs

\mathbf{m}_{ij} =\phi_{e}\left(\mathbf{h}_{i}^{l}, \mathbf{h}_{j}^{l},\left|\mathbf{x}_{i}^{l}-\mathbf{x}_{j}^{l}\right|^{2}\right)
\mathbf{x}_{i}^{l+1} =\mathbf{x}_{i}^{l}+\sum_{j \neq i} \frac{(\mathbf{x}_{i}^{l}-\mathbf{x}_{j}^{l})}{|\mathbf{x}_{i}^{l}-\mathbf{x}_{j}^{l}| + 1} \phi_{x}\left(\mathbf{m}_{ij}\right)
\mathbf{m}_{i} = \sum_{j \not= i} e_{ij}\mathbf{m}_{ij}
\mathbf{h}_{i}^{l+1} =\phi_{h}\left(\mathbf{h}_{i}^l, \mathbf{m}_{i} \right)

1. Invertible but expressive

2. Equivariant to E(n)

\mathbf{x} = \mathbf{z} + \int_1^0 \phi(\mathbf{x}(t)) dt

E(n) equivariant normalizing flows

https://arxiv.org/abs/2105.09016

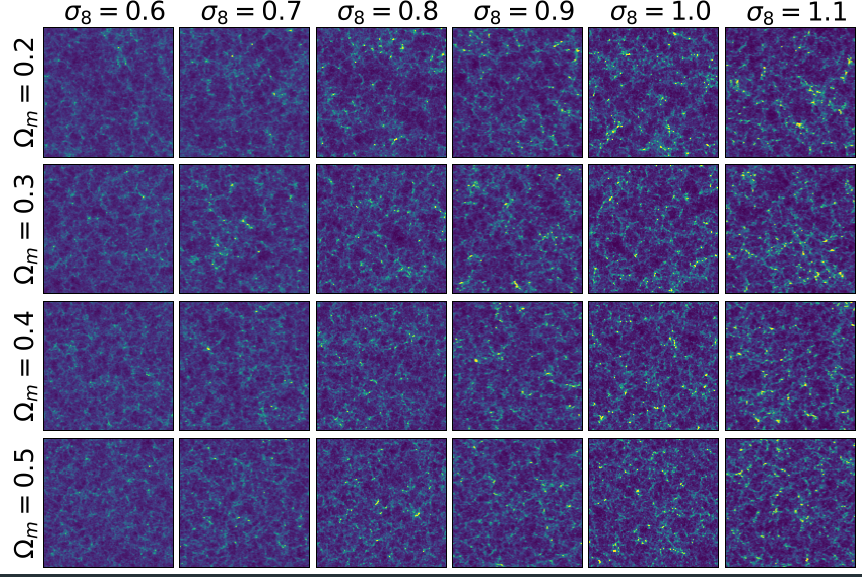
Cosmological simulations -> Millions of particles!

Solution: Density on mesh + Convolutions in Fourier space

https://arxiv.org/abs/2202.05282

\int T(\mathbf{r} - \mathbf{r}^\prime) x(\mathbf{r}^\prime) d \mathbf{r}^\prime = \hat{F}^{-1} (\hat{T}(k) \hat{x}(\mathbf{k}))
f = \green{\psi} \left(\hat{F}^{-1} \red{\hat{T}(k)} \hat{F} x \right)

1-D functions learned from data

https://arxiv.org/pdf/1906.04032.pdf

\red{\hat{T}(k)}

Cubic splines (8 spline points)

\green{\psi(x)}

Monotonic rational quadratic splines

(8 spline points)

Loss Function

Generative: Maximize likelihood

Discriminative: target the posterior

\mathcal{L} = -\frac{1}{N} \sum_i \log p(x_i|\theta)
\mathcal{L} = -\frac{1}{N} \sum_i \log p(\theta|x_i)
\mathcal{L} = -\frac{1}{N} \sum_i \left( \log p(x_i|\theta) + \log p(\theta) - log(p(\theta) \right)
p(\theta|\mathbf{x}) = \frac{p(\mathbf{x}|\theta)p(\theta)}{p(\mathbf{x})}

Gaussian Random Field:

The Power spectrum is an optimal summary statistic

Analytical likelihood

Flow likelihood

\hat{T}(k) = \frac{1}{a\sqrt{P(k)}}
\psi(x) = a x

Non-Gaussian N-body simulations

1. Inference

Non-Gaussian N-body simulations

2. Sampling

  • Can we quantify the full information content? Can normalizing flows extract all the information there is about cosmology?

 

  • Can the latent space be the initial conditions for the N-body sim?

 

  • Are current models to embed symmetries too constraining?

 

  • Model misspecification? 

 

  • Does dimensionality reduction help with interpretability?