Simulation-based inference

Boomers Quantified Uncertainty. We Simulate It

[Video Credit: N-body simulation Francisco Villaescusa-Navarro]

IAIFI Fellow

Carolina Cuesta-Lazaro

IAIFI Summer School

Why should I care?

Decision making

Decision making in science

Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference

Is the current Standard Model ruled out by data?

Mass density

Vacuum Energy Density

CMB

Supernovae

\Omega_m

\Omega_\Lambda

Observation

Ground truth

Prediction

Uncertainty

Is it safe to drive there?

Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference

Better data needs better models

p(\mathrm{theory} | \mathrm{data})

Interpretable Simulators

Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference

\mathrm{data}

\mathrm{theory}

Uncertainties are everywhere

x^i_1

x^i_2

Noise in features

+ correlations

Noise in finite data realization

\{x^1, x^2,...,x^N \}

\theta

p(\theta|x)

\phi

Uncertain parameters

Limited model architecture

Imperfect optimization

N \gg 1

Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference

Ensembling / Bayesian NNs

\theta

Forward Model

Observable

\color{darkgray}{\Omega_m}, \color{darkgreen}{w_0, w_a},\color{purple}{f_\mathrm{NL}}\, ...

Dark matter

Dark energy

Inflation

Predict

Infer

Parameters

Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference

Inverse mapping

\color{darkgray}{\sigma}, \color{darkgreen}{v}, ...

Fault line stress

Plate velocity

q_\phi(\theta|x) \approx

Variational

Posterior

\color{white}{p(\theta|x)} \color{black}{=} \frac{\color{white}{p(x|\theta)} \color{white}{p(\theta)}}{\color{white}{p(x)}}

Likelihood

Posterior

Prior

Evidence

p(\theta|x)

p(x|\theta)

p(\theta)

p(x)

Markov Chain Monte Carlo MCMC

Hamiltonian Monte Carlo HMC

Variational Inference VI

Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference

p(x) = \int p(x|\theta) p(\theta) d\theta

If can evaluate posterior (up to normalization), but not sample

Intractable

Unknown likelihoods

Amortized inference

Scaling high-dimensional

Marginalization nuisance

Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference

Image Credit: Chi Feng mcmc demo

Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference

["Polychord: nested sampling for cosmology" Handley et al]

["Fluctuation without dissipation: Microcanonical Langevin Monte Carlo" 
Robnik and Seljak]

The price of sampling

Higher Effective Sample Size (ESS) = less correlated samples

Number of Simulator Calls

Known likelihood

Differentiable simulators

The simulator samples the likelihood

Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference

x_\mathrm{final}, y_\mathrm{final} \sim \mathrm{Simulator}(f, \theta) = p(x_\mathrm{final}, y_\mathrm{final} \mid f, \theta)

p(x_\mathrm{final}, y_\mathrm{final}|f, \theta) = \int dz p(x_\mathrm{final}, y_\mathrm{final},z|f, \theta)

z: All possible trajectories

Maximize the likelihood of the training samples

\hat \phi = \argmax \left[ \log p_\phi (x_\mathrm{train}|\theta_\mathrm{train}) \right]

Model

p_\phi(x)

Training Samples

x_\mathrm{train}

Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference

Neural Likelihood Estimation NLE

x_\mathrm{final}, y_\mathrm{final} \sim p(x_\mathrm{final}, y_\mathrm{final} \mid f, \theta) p(f, \theta)

NLE

No implicit prior

Not amortized

Goodness-of-fit

Scaling with dimensionality of x

p(x|\theta)

Implicit marginalization

\mathcal{L}(\phi) \approx -\frac{1}{N} \sum_{i=1}^N \log q_\phi(x_i \mid \theta_i )

Neural Posterior Estimation NPE

D_{\text{KL}}(p(\theta \mid x) \parallel q_\phi(\theta \mid x)) = \mathbb{E}_{\theta \sim p(\theta \mid x)} \log \frac{p(\theta \mid x)}{q_\phi(\theta \mid x)}

Loss Approximate variational posterior, q, to true posterior, p

q_\phi(\theta \mid x)

p(\theta \mid x)

Image Credit: "Bayesian inference; How we are able to chase the Posterior" Ritchie Vink

Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference

KL Divergence

\mathcal{L}(\phi) = -\mathbb{E}_{\theta \sim p(\theta \mid x)} \left[ \log q_\phi(\theta \mid x) \right]

\mathcal{L}(\phi) = -\int p(\theta \mid x) \log q_\phi(\theta \mid x) \, d\theta

= -\int \frac{p(x \mid \theta) p(\theta)}{p(x)} \log q_\phi(\theta \mid x) \, d\theta.

\propto -\int p(x \mid \theta) p(\theta) \log q_\phi(\theta \mid x) \, d\theta.

D_{\text{KL}}(p(\theta \mid x) \parallel q_\phi(\theta \mid x)) = \mathbb{E}_{\theta \sim p(\theta \mid x)} \log \frac{p(\theta \mid x)}{q_\phi(\theta \mid x)}

Need samples from true posterior

Run simulator

Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference

p(x,\theta)

\phi^* = \argmin_{\phi}

Minimize KL

\mathbb{E}_{p(\theta, x)}

\mathcal{L}(\phi) \approx -\frac{1}{N} \sum_{i=1}^N \log q_\phi(\theta_i \mid x_i)

\mathcal{L}(\phi) = -\mathbb{E}_{(\theta, x) \sim p(\theta, x)} \left[ \log q_\phi(\theta \mid x) \right]

(\theta_i, x_i) \sim p(\theta, x)

Amortized Inference!

Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference

Run simulator

Neural Posterior Estimation NPE

Neural Compression

s = F_\eta(x)

High-Dimensional

Low-Dimensional

Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference

p(\theta|x) = p(\theta|s)

s is sufficient iif

Neural Compression: MI

I(s(x), \theta)

Maximise

Mutual Information

I(\theta, s(x)) = D_{\text{KL}}(p(\theta, s(x)) \parallel p(\theta)p(s(x)))

\theta, s(x) \, \, \mathrm{independent} \rightarrow p(\theta, s(x)) = p(\theta)p(s(x))

s(x)

\theta

I(s(x), \theta)

\theta, s(x)

Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference

I(\theta, s(x)) = \mathbb{E}_{p(\theta, s(x))} \left[ \log \frac{p(\theta, s(x))}{p(\theta)p(s(x))} \right]

= \mathbb{E}_{p(\theta, s(x))} \left[ \log \frac{p(\theta \mid s(x))p(s(x))}{p(\theta) p(s(x))} \right]

p(\theta, s(x)) = p(\theta \mid s(x)) p(s(x))

Need true posterior!

I(\theta, s(x)) \approx \mathbb{E}_{p(\theta, s(x))} \left[ \log \frac{q_\phi(\theta \mid s(x))}{p(\theta)} \right]

\mathcal{L}(\phi, \eta) \approx -\frac{1}{N} \sum_{i=1}^N \log q_\phi(\theta_i \mid s_\eta(x_i))

Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference

NLE

No implicit prior

Not amortized

Goodness-of-fit

Scaling with dimensionality of x

p(x|\theta)

NPE

p(\theta|x)

Amortized

Scales well to high dimensional x

Goodness-of-fit

Fixed prior

Implicit marginalization

\mathcal{L}(\phi) \approx -\frac{1}{N} \sum_{i=1}^N \log q_\phi(\theta_i \mid x_i)

\mathcal{L}(\phi) \approx -\frac{1}{N} \sum_{i=1}^N \log q_\phi(x_i \mid \theta_i )

Implicit marginalization

Do we actually need Density Estimation?

Just use binary classifiers!

x, \theta \sim p(x,\theta)

x, \theta \sim p(x)p(\theta)

y = 1

y = 0

\theta

Binary cross-entropy

Sample from simulator

Mix-up

Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference

Likelihood-to-evidence ratio

r(x,\theta) = \frac{p(x\mid \theta)}{p(x)}

Likelihood-to-evidence ratio

p(x,\theta|y) = p(x,\theta) \, \, \mathrm{if} \, \, y=1

p(x,\theta|y) = p(x)p(\theta) \, \, \mathrm{if} \, \, y=0

p(y=1 \mid x,\theta) = \frac{p(x,\theta|y=1)p(y)}{p(x,\theta)}

\left(p(x,\theta \mid y=0) + p(x,\theta \mid y=1) \right)p(y)

p(y=1 \mid x,\theta) = \frac{p(x,\theta)}{p(x)p(\theta) + p(x,\theta)}

= \frac{p(x,\theta)}{p(x)p(\theta)}

= \frac{r(x,\theta)}{r(x,\theta) + 1}

Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference

\frac{p(y=1 \mid x,\theta)}{p(y=0 \mid x,\theta)} = \frac{p(y=1 \mid x,\theta)}{1 - p(y=0 \mid x,\theta)}

p(y=1 \mid x,\theta) = \sigma(s(x,\theta)) = \frac{1}{1 + \exp^{-s(x,\theta)}}

\frac{p(y=1 \mid x,\theta)}{p(y=0 \mid x,\theta)} = \exp^{s(x,\theta)}

s(x,\theta) = \log \left( \frac{p(y=1 \mid x,\theta)}{p(y=0 \mid x,\theta)} \right) = \log(r(x,\theta))

Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference

Classifier logits

log(Likelihood-to-evidence ratio)

NLE

No implicit prior

Not amortized

Goodness-of-fit

Scaling with dimensionality of x

p(x|\theta)

NPE

p(\theta|x)

NRE

\frac{p(x|\theta)}{p(x)}

Amortized

Scales well to high dimensional x

Goodness-of-fit

Fixed prior

Implicit marginalization

\mathcal{L}(\phi) \approx -\frac{1}{N} \sum_{i=1}^N \log q_\phi(\theta_i \mid x_i)

\mathcal{L}(\phi) \approx -\frac{1}{N} \sum_{i=1}^N \log q_\phi(x_i \mid \theta_i )

No need variational distribution

No implicit prior

Implicit marginalization

Approximately normalised

\begin{split} L &= - \frac{1}{N} \sum_{i=1}^N \left[ y_i \log(p_i) \right. \\ &\left. + (1 - y_i) \log(1 - p_i) \right] \end{split}

Not amortized

Implicit marginalization

Density Estimation 101

Maximize the likelihood of the training samples

\hat \phi = \argmax \left[ \log p_\phi (x_\mathrm{train}) \right]

x_1

x_2

Model

p_\phi(x)

Training Samples

x_\mathrm{train}

Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference

x_1

x_2

Trained Model

p_\phi(x)

Evaluate probabilities

Low Probability

High Probability

Generate Novel Samples

Simulator

Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference

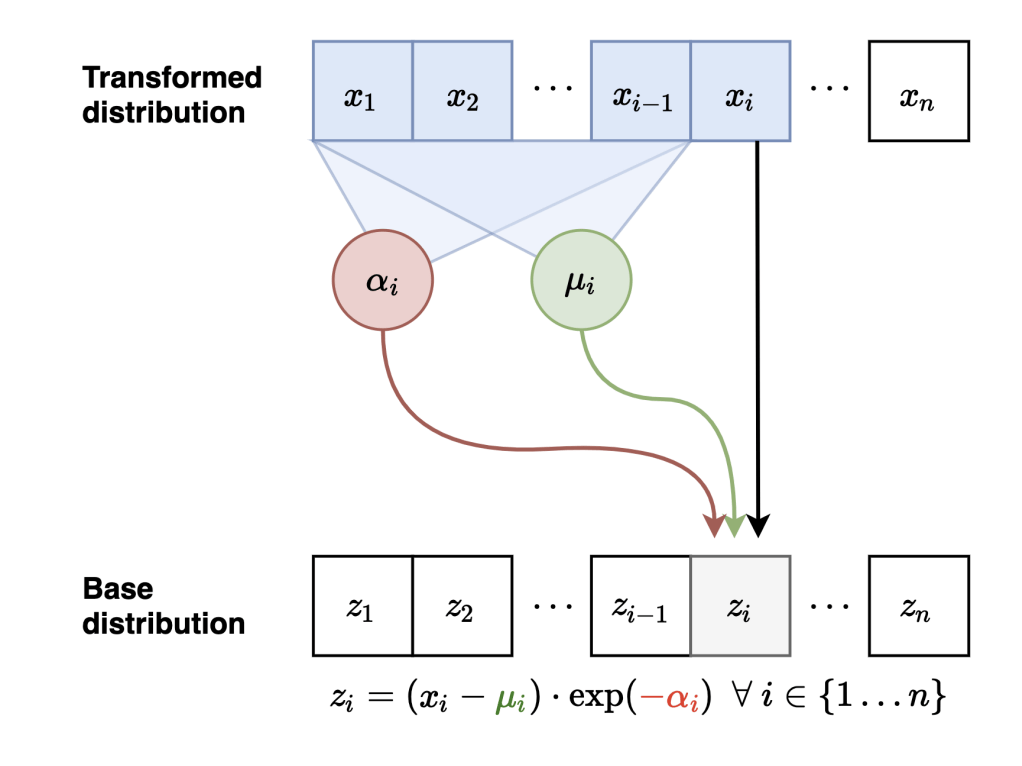
Normalizing flows

[Image Credit: "Understanding Deep Learning" Simon J.D. Prince]

z \sim p(z)

x \sim p(x)

x = f(z)

p(x) = p(z = f^{-1}(x)) \left| \det J_{f^{-1}}(x) \right|

Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference

Bijective

Sample

Evaluate probabilities

Probability mass conserved locally

z_0 \sim p(z)

z_k = f_k(z_{k-1})

\log p(x) = \log p(z_0) - \sum_{k=1}^{K} \log \left| \det J_{f_k} (z_{k-1}) \right|

Image Credit: "Understanding Deep Learning" Simon J.D. Prince

Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference

Masked Autoregressive Flows

p(x) = \prod_i{p(x_i \,|\, x_{1:i-1})}

p(x_i \,|\, x_{1:i-1}) = \mathcal{N}(x_i \,|\,\mu_i, (\exp\alpha_i)^2)

\mu_i, \alpha_i = f_{\phi_i}(x_{1:i-1})

Neural Network

x_i = z_i \exp(\alpha_i) + \mu_i

z_i = (x_i - \mu_i) \exp(-\alpha_i)

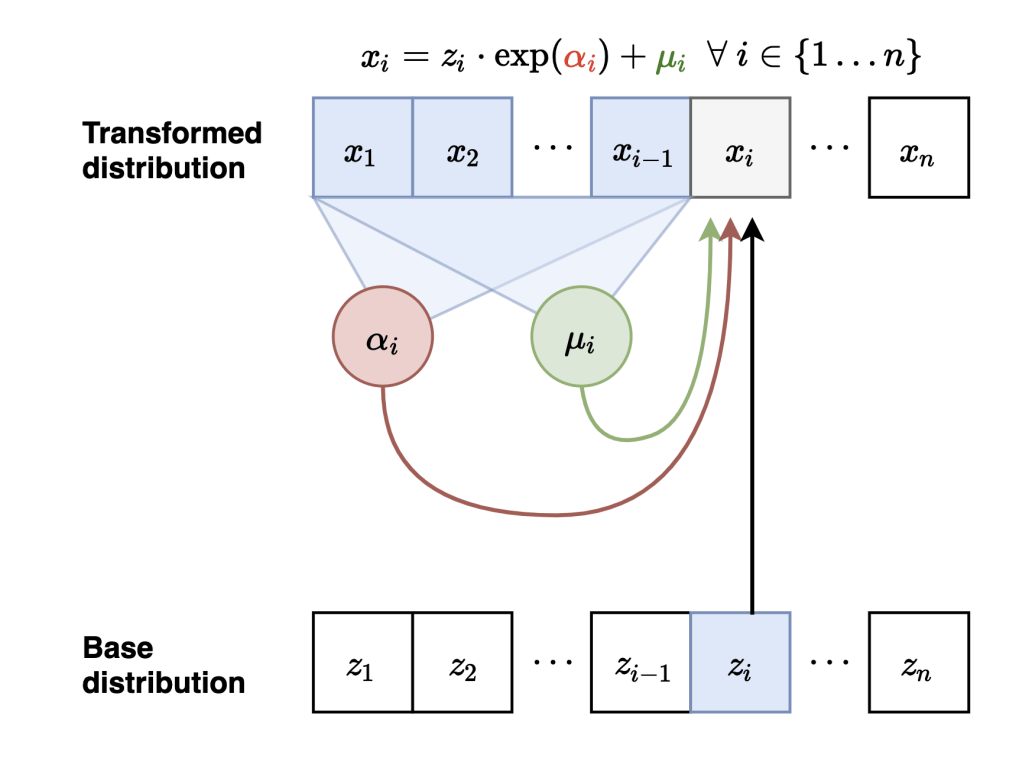
Sample

Evaluate probabilities

\frac{dz_t}{dt} = u^\phi_t(z_t)

x = z_0 + \int_0^1 u^\phi_t(z_t) dt

Continuity equation

\frac{d p(z_t)}{dt} = - \nabla \left( u^\phi_t(z_t) p(z_t) \right)

[Image Credit: "Understanding Deep Learning" Simon J.D. Prince]

Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference

Continuous time Normalizing flows

\log p(x) = \log p(z_0) + \int_0^1 \mathrm{Tr} J_{u^\phi_t} (z_t) dt

Need to solve this expensive integral at each step during training to maximise likelihood!

Very slow -> Difficult to scale to high dims

Can we avoid it?

\frac{d p(z_t)}{dt} = - \nabla \left( u^\phi_t(z_t) p(z_t) \right)

Restricted trajectories: flow matching / diffusion

Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference

Flow matching

\mathcal{L} = \mathbb{E}_{t \sim \mathcal{U}[0, 1]} \mathbb{E}_{x_t \sim p_t}\left[\| u_t^\phi(x_t) - u_t(x_t) \|^2 \right]

Regress the velocity field directly!

[Image Credit: "An Introduction to flow matchig" Tor Fjelde et al]

Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference

["Flow Matching for Generative Modeling" Lipman et al]

["Stochastic Interpolants: A Unifying framework for Flows and Diffusions" Albergo et al]

Conditional Flow matching

x_t = (1-t) x_0 + t x_1

\mathcal{L}_\mathrm{conditional} = \mathbb{E}_{t,x_0,x_1}\left[\| u_t^\phi(x_t) - u_t(x_0,x_1) \|^2 \right]

Assume a conditional vector field (known at training time)

The loss that we can compute

The gradients of the losses are the same!

\nabla_\phi \mathcal{L}_\mathrm{conditional} = \nabla_\phi \mathcal{L}

x_0

x_1

Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference

["Flow Matching for Generative Modeling" Lipman et al]

["Stochastic Interpolants: A Unifying framework for Flows and Diffusions" Albergo et al]

u_t(x) = \int u_t(x|x_1) \frac{p_t(x|x_1) p_1(x_1)}{p_t(x)} \, dx_1

p_t(x) = \int p_t(x|x_1) q(x_1) \, dx_1

Intractable

Flow Matching

\frac{dz_t}{dt} = u^\phi_t(z_t)

x = z_0 + \int_0^1 u^\phi_t(z_t) dt

Continuity equation

\frac{d p(z_t)}{dt} = - \nabla \left( u^\phi_t(z_t) p(z_t) \right)

[Image Credit: "Understanding Deep Learning" Simon J.D. Prince]

Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference

Sample

Evaluate probabilities

Diffusion models

Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference

p(z_1|z_0)

p(z_0)

p(z_T)

p(z_2)

p(z_1)

p(z_2|z_1)

p(z_T|z_2)

Reverse diffusion: Denoise previous step

Forward diffusion: Add Gaussian noise (fixed)

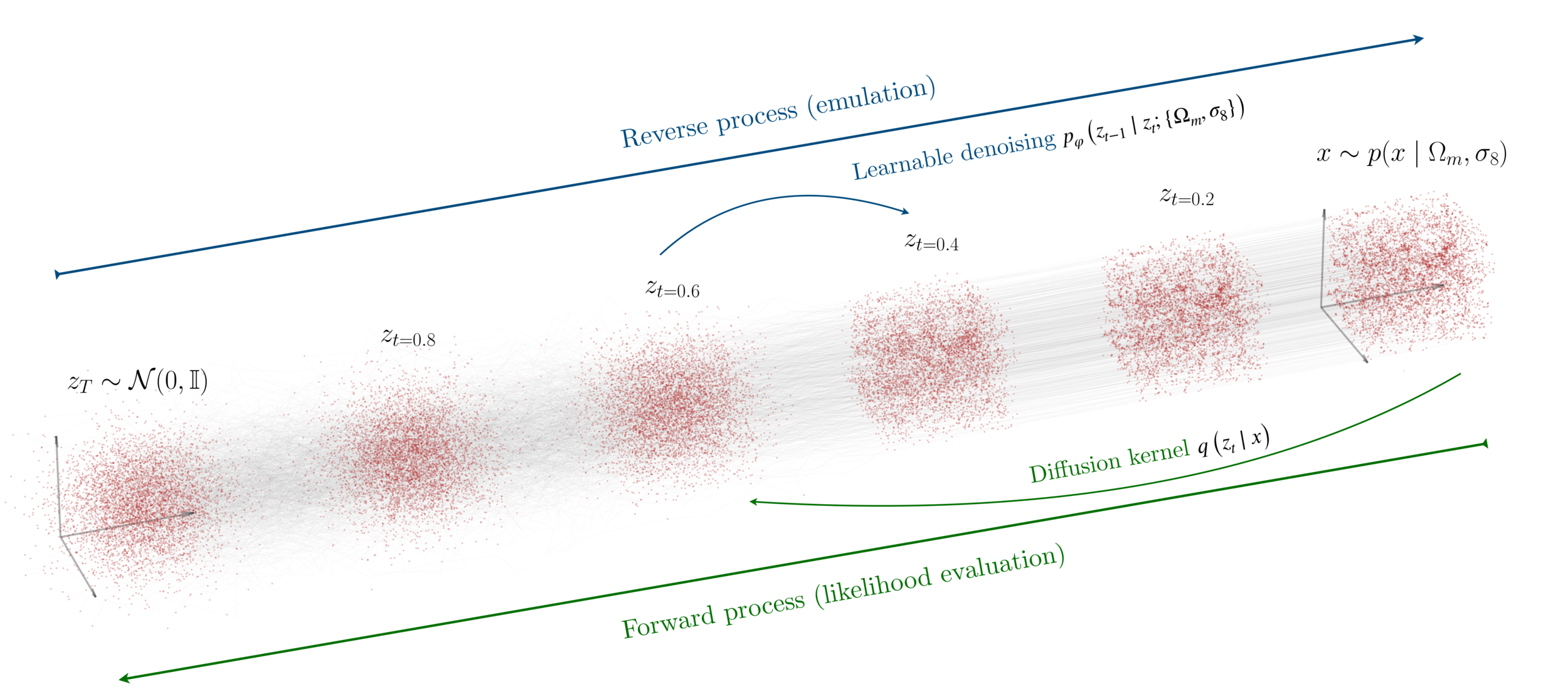
["A point cloud approach to generative modeling for galaxy surveys at the field level" 
Cuesta-Lazaro and Mishra-Sharma

arXiv:2311.17141]

Siddharth Mishra-Sharma

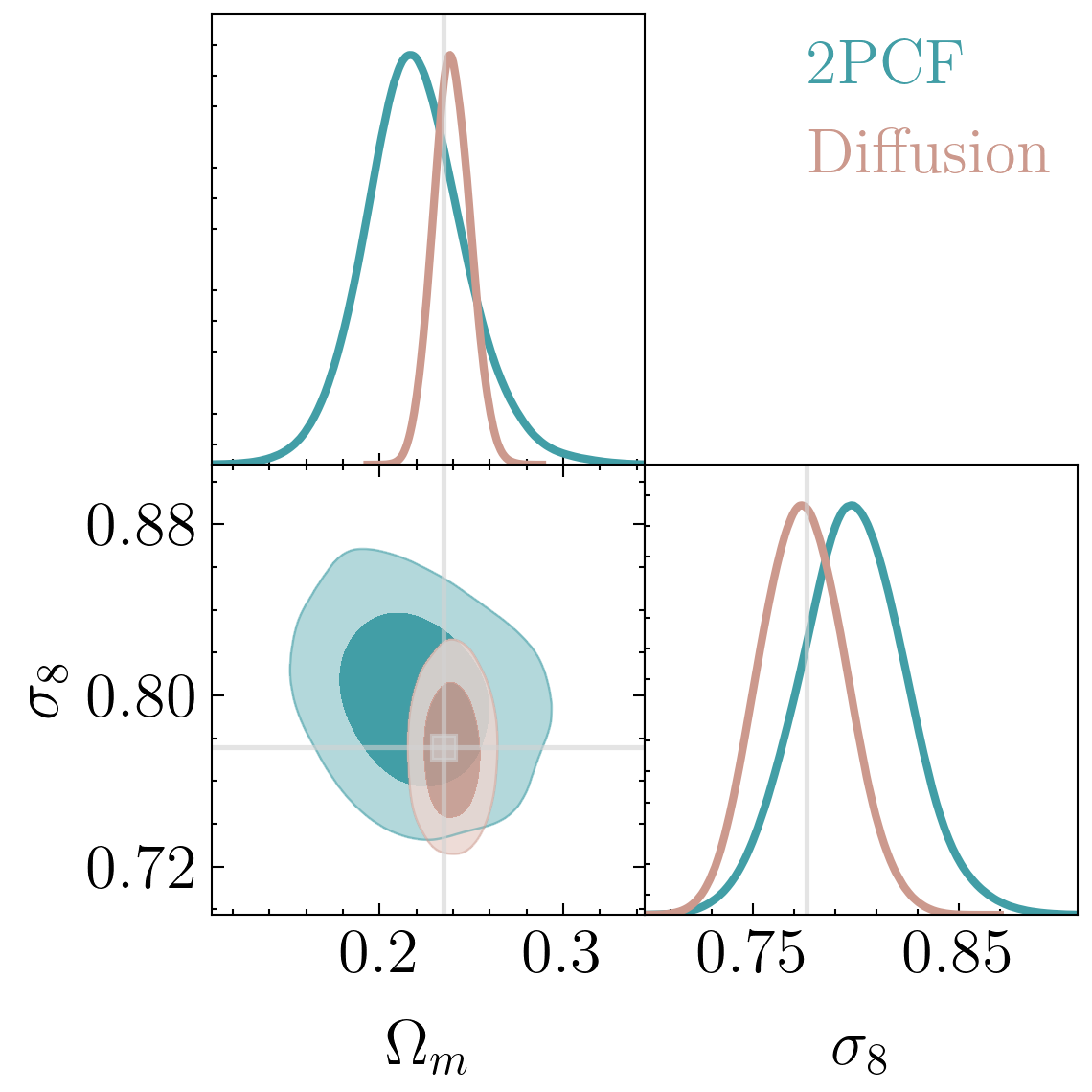
Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference

Galaxies as point clouds

NLE

No implicit prior

Not amortized

Goodness-of-fit

Scaling with dimensionality of x

p(x|\theta)

NPE

p(\theta|x)

NRE

\frac{p(x|\theta)}{p(x)}

Amortized

Scales well to high dimensional x

Goodness-of-fit

Fixed prior

Implicit marginalization

\mathcal{L}(\phi) \approx -\frac{1}{N} \sum_{i=1}^N \log q_\phi(\theta_i \mid x_i)

\mathcal{L}(\phi) \approx -\frac{1}{N} \sum_{i=1}^N \log q_\phi(x_i \mid \theta_i )

No need variational distribution

No implicit prior

Implicit marginalization

Approximately normalised

\begin{split} L &= - \frac{1}{N} \sum_{i=1}^N \left[ y_i \log(p_i) \right. \\ &\left. + (1 - y_i) \log(1 - p_i) \right] \end{split}

Not amortized

Implicit marginalization

How good is your posterior?

Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference

Test log likelihood

["Benchmarking simulation-based inference" 
Lueckmann et al

arXiv:2101.04653]

\mathbb{E}_{p(x,\theta)} \log \hat{p}(\theta \mid x)

Posterior predictive checks

Observed

Re-simulated posterior samples

Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference

Classifier 2 Sample Test (C2ST)

\mathrm{R} \sim p(\theta|x)

\mathrm{F} \sim \hat{p}(\theta|x)

Real or Fake?

Benchmarking SBI

Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference

["Benchmarking simulation-based inference" 
Lueckmann et al

arXiv:2101.04653]

Classifier 2 Sample Test (C2ST)

Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference

["A Trust Crisis In Simulation-Based Inference? Your Posterior Approximations Can Be Unfaithful" 
Hermans et al

arXiv:2110.06581]

Much better than overconfident!

Coverage: assessing uncertainties

\int_\Theta \hat{p}(\theta \mid x = x_0) d\theta = 1 - \alpha

Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference

["A Trust Crisis In Simulation-Based Inference? Your Posterior Approximations Can Be Unfaithful" 
Hermans et al

arXiv:2110.06581]

Credible region (CR)

Not unique

High Posterior Density region (HPD)

Smallest "volume"

True value in CR with

1 - \alpha

probability

\theta^*

\mathcal{H}

Empirical Coverage Probability (ECP)

\mathrm{ECP} = \mathbb{E}_{p(x,\theta)} \left[ \mathbb{1} \left[ \theta \in \mathcal{H}_{\hat{p}(\theta|x)}(1-\alpha)\right] \right]

Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference

["Investigating the Impact of Model Misspecification in Neural Simulation-based Inference" 
Cannon et al arXiv:2209.01845 ]

Underconfident

Overconfident

Expected Coverage Probability (ECP)

\mathrm{ECP} = \mathbb{E}_{p(x,\theta)} \left[ \mathbb{1} \left[ \theta \in \mathcal{H}_{\hat{p}(\theta|x)}(1-\alpha)\right] \right]

Hard to find in high dimensions!

(x^*, \theta^*) \rightarrow

\left \{ \theta \in U \mid \hat{p}(\theta|x^*) \geq \hat{p}(\theta^*|x^*) \right \}

\theta^*

\mathcal{H}

\mathrm{ECP} = \mathbb{E}_{p(x,\theta)} \left[ \mathbb{1} \left[ \alpha_\mathrm{U}(\hat{p}, \theta^*, x^*) \geq \alpha \right]\right]

Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference

1-\alpha_\mathrm{U}

\leq 1-\alpha

Underconfident

Overconfident

["Sampling-Based Accuracy Testing of Posterior Estimators for General Inference" Lemos et al arXiv:2302.03026]

["Investigating the Impact of Model Misspecification in Neural Simulation-based Inference" 
Cannon et al arXiv:2209.01845 ]

Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference

Calibrated doesn't mean informative!

Always look at information gain too

\mathrm{ECP} = \mathbb{E}_{p(x,\theta)} \left[ \mathbb{1} \left[ \theta \in \mathcal{H}(\hat{p}, \alpha) \right] \right]

= \mathbb{E}_{p(\theta)} \left[ \mathbb{1} \left[ \theta \in \mathcal{H}(\hat{p}, \alpha) \right] \right]

\hat{p}(\theta \mid x) = p(\theta)

= \int_{\mathcal{H}(\hat{p}),\alpha} d\theta p(\theta)

\mathbb{E}_{p(x,\theta)} \left[ \log \hat{p}(\theta \mid x) - \log p(\theta) \right]

Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference

= 1 - \alpha

Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference

["A Trust Crisis In Simulation-Based Inference? Your Posterior Approximations Can Be Unfaithful" 
Hermans et al

arXiv:2110.06581]

["Calibrating Neural Simulation-Based Inference with Differentiable Coverage Probability" 
Falkiewicz et al

arXiv:2310.13402]

["A Trust Crisis In Simulation-Based Inference? Your Posterior Approximations Can Be Unfaithful" 
Hermans et al

arXiv:2110.06581]

Sequential SBI

Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference

["Benchmarking simulation-based inference" 
Lueckmann et al

arXiv:2101.04653]

[Image credit: https://www.mackelab.org/delfi/]

Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference

Sequential SBI

Sequential Neural Likelihood Estimation

["Sequential Neural Likelihood: Fast Likelihood-free Inference with Autoregressive Flows" 
Papamakarios et al

arXiv:1805.07226]

\theta \sim \overset{\sim}{p} (\theta)

Proposal (different from prior)

\overset{\sim}{p} (x,\theta) = p(x|\theta)\overset{\sim}{p}(\theta)

\mathbb{E}_{\overset{\sim}{p}(x,\theta)} \log q_\phi (x|\theta) =

\mathrm{D}_\mathrm{KL}(P(x) \mid \mid Q(x)) = \mathbb{E}_{P(x)} \left(\frac{\log P(x)}{\log Q(x)} \right)

= - \mathbb{E}_{\overset{\sim}{p} (\theta) } \left(\mathrm{D}_\mathrm{KL}(p(x|\theta) \mid \mid q_\phi(x|\theta) \right) + \mathrm{C}

Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference

SNLE

\overset{\sim}{p}(\theta \mid x_0) \propto p(\theta \mid x_0)\frac{\overset{\sim}{p}(\theta)}{p(\theta)}

["Fast -free Inference of Simulation Models with Bayesian Conditional Density Estimation" 
Papamakarios et al

arXiv:1605.06376]

["Flexible statistical inference for mechanistic models of neural dynamics." 
Lueckmann et al

arXiv:1711.01861]

Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference

Sequential can't be amortized!

Sequential Neural Posterior Estimation

SNPE

\theta \sim \overset{\sim}{p} (\theta)

Proposal (different from prior)

Real life scaling: Gravitational lensing

["A Strong Gravitational Lens Is Worth a Thousand Dark Matter Halos: Inference on Small-Scale Structure Using Sequential Methods" 
Wagner-Carena et al arXiv:2404.14487]

Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference

Current SBI limitations

Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference

["All-in-one simulation-based inference" Gloeckler et al arXiv:2404.09636]

Model all conditionals at once!

All-in-one: The Simformer

Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference

["All-in-one simulation-based inference" Gloeckler et al arXiv:2404.09636]

Score based diffusion model with sampled conditional masks

smsharma/awesome-neural-sbi

Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference

Model mispecification

Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference

["Investigating the Impact of Model Misspecification in Neural Simulation-based Inference" 
Cannon et al arXiv:2209.01845]

More misspecified

SBI Resources

Carolina Cuesta-Lazaro IAIFI/MIT - Simulation-Based Inference

smsharma/awesome-neural-sbi

"The frontier of simulation-based inference" Kyle Cranmer, Johann Brehmer, and Gilles Louppe

sbi-dev/sbi

probabilists/zuko

dirmeier/sbijax

Github repos

Review

cuestalz@mit.edu

Book

"Probabilistic Machine Learning: Advanced Topics" Kevin P. Murphey