Initial Conditions Reconstruction with Stochastic Interpolants

[Video Credit: N-body simulation Francisco Villaescusa-Navarro]

Carolina Cuesta-Lazaro

IAIFI Fellow, MIT / Center for Astrophysics

Adrian E. Bayer, Michael S. Albergo, Siddharth Mishra-Sharma, Chirag Modi, Daniel J. Eisenstein

Carolina Cuesta-Lazaro IAIFI/MIT @ ML4PS 2024

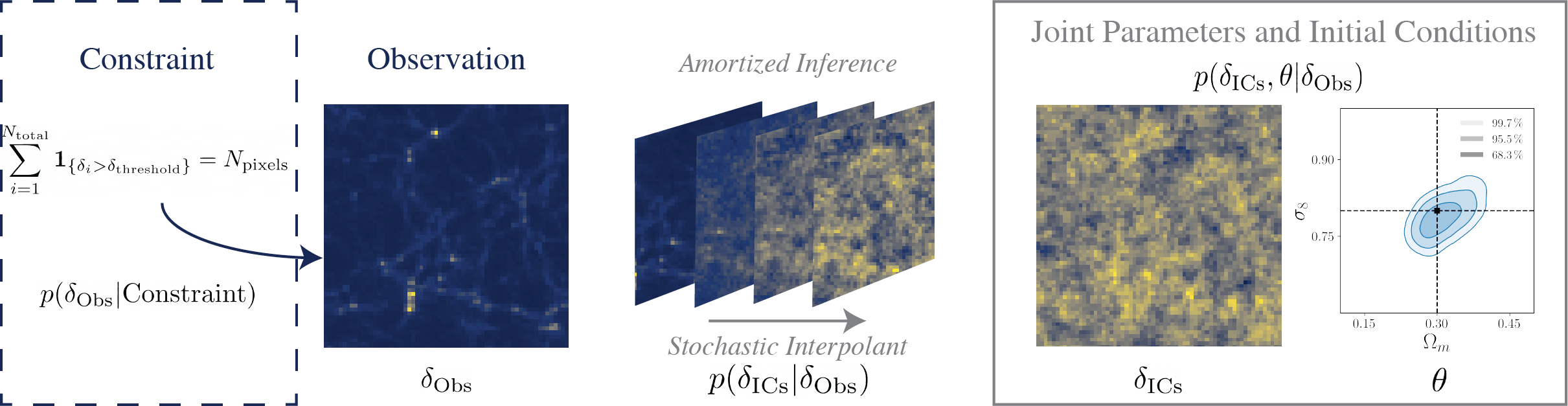
Initial Conditions

early Universe

Cosmological Parameters

theory

\mathit{O}(2048^3)
p(\delta_{\mathrm{ICs}}, \mathcal{\theta}|\delta_{\mathrm{Obs}})

Carolina Cuesta-Lazaro IAIFI/MIT @ ML4PS 2024

?

Observed Density Field

today

\mathit{O}(10)
\mathit{O}(2048^3)
+
\Omega_m,
\sigma_8

Hamiltonian Monte Carlo

1) Likelihood is intractable for realistic scenarios, but can get samples from simulator

2) Forward model has to be differentiable

(and relatively fast)

3) Not amortized

\log P(\delta_\mathrm{Obs}|\delta_\mathrm{ICs}, \mathcal{C}) = -\frac{1}{2} \sum_i \left(\frac{\mathcal{S}^i[\delta_{\mathrm{ICs}}, \mathcal{C}] - \delta_{\mathrm{Obs}}^i}{\sigma} \right)^2 
["Field-Level Inference with Microcanonical Langevin Monte Carlo" 
Bayer, Seljak, Modi arXiv:2307.09504]
["Bayesian physical reconstruction of initial conditions from large scale structure surveys" 
Jasche, Wandelt arXiv:1203.3639]

Carolina Cuesta-Lazaro IAIFI/MIT @ ML4PS 2024

["Posterior Sampling of the Initial Conditions of the Universe from Non-linear Large Scale Structures using Score-Based Generative Models" 
Legin et al arXiv:2304.03788]
\frac{dx_t}{dt} = v_\phi(t,x_t)
x_1 = x_0 + \int_0^1 v_\phi(t,x_t) dt
\frac{d p(x_t)}{dt} = - \nabla \left( v_\phi(t,x_t) p(x_t) \right)

Continuity Equation

Diffusion, Flow matching, Interpolants... 

[Image Credit: "Understanding Deep Learning" Simon J.D. Prince]

Data

Base

Continuous Time Normalizing Flows

Carolina Cuesta-Lazaro IAIFI/MIT @ ML4PS 2024

Missing pieces:

Simulation-free loss

SDE formulation

Can we regress the velocity field?

= (1-t)x_0 + t x_1
b(t,x, x_0) = \mathbb{E}\left[\partial_t I + \partial_t \gamma(t) \sqrt{t} z| x_t = x \right]

Simulation-free!

I_t = \alpha_t x_0 + \beta_t x_1

Interpolant

+ \gamma_t W_t

Expectation over all possible paths that go through xt

["Stochastic Interpolants: A Unifying framework for flows and diffusion" 
Albergo et al arXiv:2303.08797]

Carolina Cuesta-Lazaro IAIFI/MIT @ ML4PS 2024

Stochastic Interpolants

dX_t = b(t, X_t, x_0) dt + \sigma_t dW_t

Stochastic

\mathcal{L} = \int_0^1 \mathbb{E}_{p(x_0,x_1), p(z)} |\hat{b}_\phi(t,x,x_0) - \partial_t I(t,x_0,x_1) - \partial_t \gamma(t) z|^2 dt
z \sim N(0,1)
\gamma(0) = \gamma(1) = 0
W_t = \sqrt{t} z

Generative SDE

Generative SDE

Carolina Cuesta-Lazaro IAIFI/MIT @ ML4PS 2024

dX_t = b_t(X_t, x_0) dt + \sigma_t dW_t

3D U-Net

True

Reconstructed

\delta_\mathrm{Obs}
\delta_\mathrm{ICs}

Carolina Cuesta-Lazaro IAIFI/MIT @ ML4PS 2024

Initial Conditions

Finals

L = 400 h^{-1} \mathrm{Mpc}, N = 32^3
L = 100 h^{-1} \mathrm{Mpc}, N = 64^3

Stochastic Interpolants

NF

p(\delta_\mathrm{ICs}, \theta|\delta_\mathrm{Obs}) =
p(\delta_\mathrm{ICs}|\delta_\mathrm{Obs})
p(\theta|\delta_\mathrm{ICs},\delta_\mathrm{Obs})

Carolina Cuesta-Lazaro IAIFI/MIT @ ML4PS 2024

(Marginalizing over parameters)

1) Likelihood not necessarily Gaussian

2) Forward model no need differentiable

3) Amortized

\mathrm{SI}:
\mathrm{SI}:
\mathrm{HMC}:
p(\delta_{\mathrm{ICs}}|\mathrm{Condition})

Carolina Cuesta-Lazaro IAIFI/MIT @ ML4PS 2024

N(\delta > \delta_\mathrm{th}) = \sum_i \Theta(\delta_i - \delta_\mathrm{th})

Sampling entire consistent trajectories, rather than just Initial Conditions

Scaling to large observed volumes

\mathcal{O}(5026^3)

Training on small volume simulations

Carolina Cuesta-Lazaro IAIFI/MIT @ ML4PS 2024

# To Do

p(\delta_{\mathrm{ICs}}, \mathcal{\theta}|\delta_{\mathrm{Obs}})

?

Controllable Simulations