Corentin Cadiou
Online @ Hyderabad 10/07/24

How chaotic is galaxy formation?
Based on work by A. Storck, Z. Kocjan, E. Pichon-Pharabod
Cadiou, Pontzen & Peiris 21 · Cadiou, Pontzen +21 · Kocjan, Cadiou, Agertz, Pontzen 24 · Cadiou, Pichon-Pharabod+24
My interests:
- Cosmic web
- DM halo formation
- Halo-galaxy connection
- Cosmological accretion
- Galaxy kinematics
and high-performance computing & visualisation
Intrinsic alignment measurement: Ganeshaiah Veena+ 19 · Alignment: M. Sachs
Neighbouring galaxies' shapes are aligned
(on the plane of the sky)
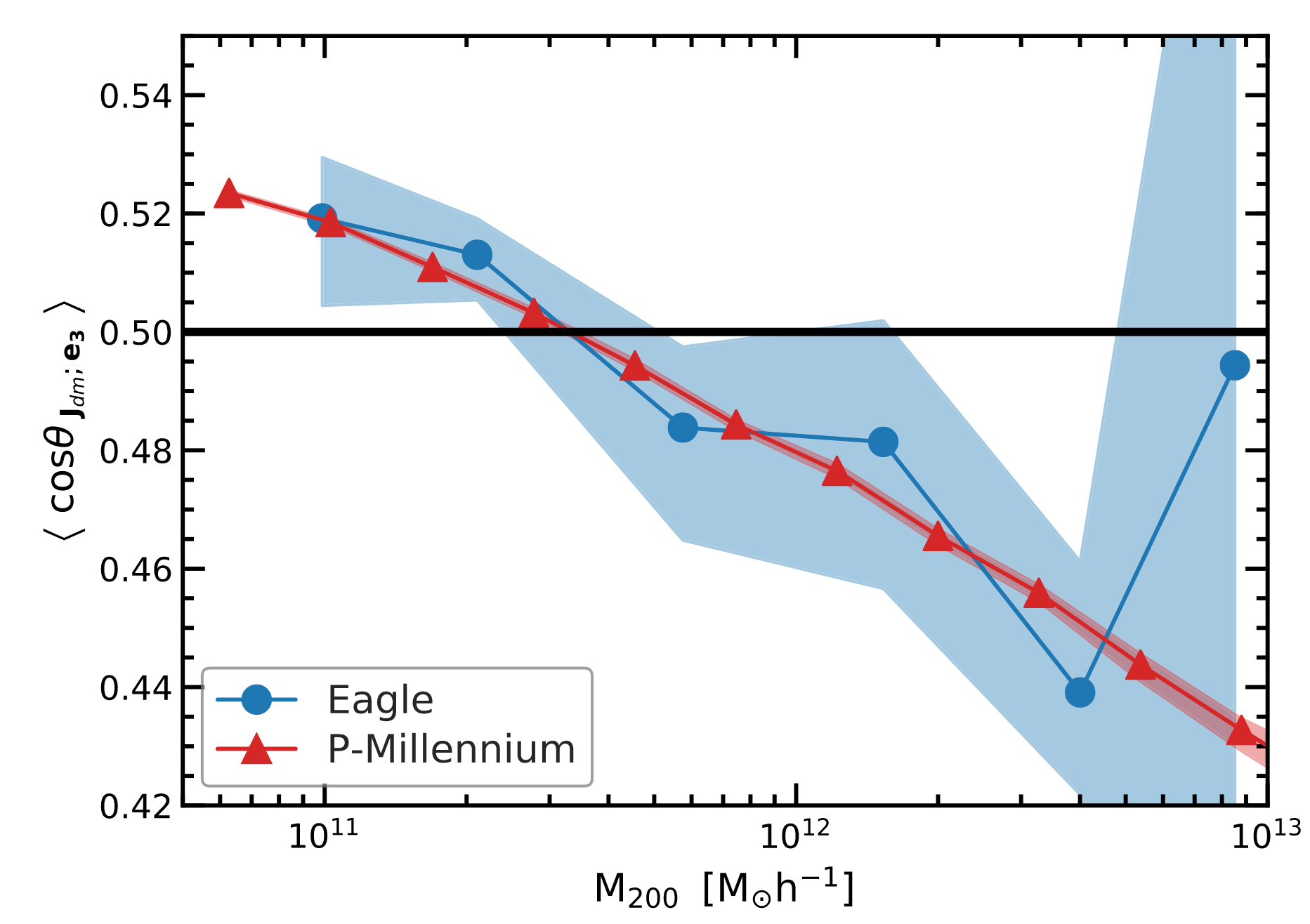
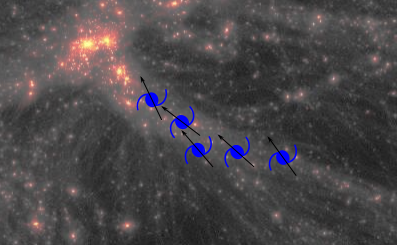
Intrinsic alignment
Baryon dominated?
No cosmo information?
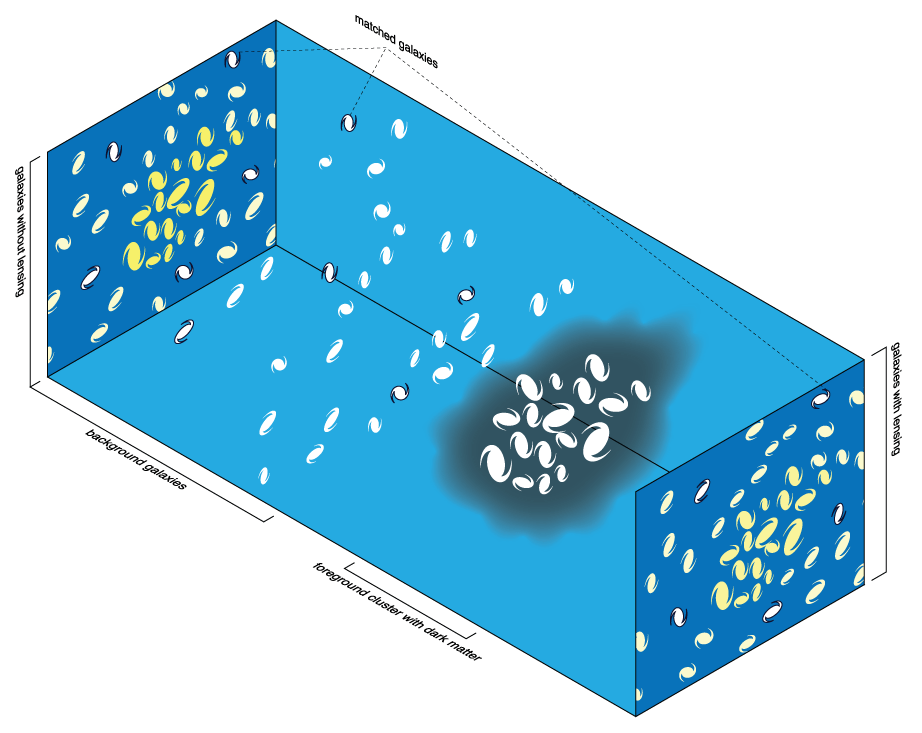
Weak lensing
L.o.s. measurement of
dark matter density
+
⇒

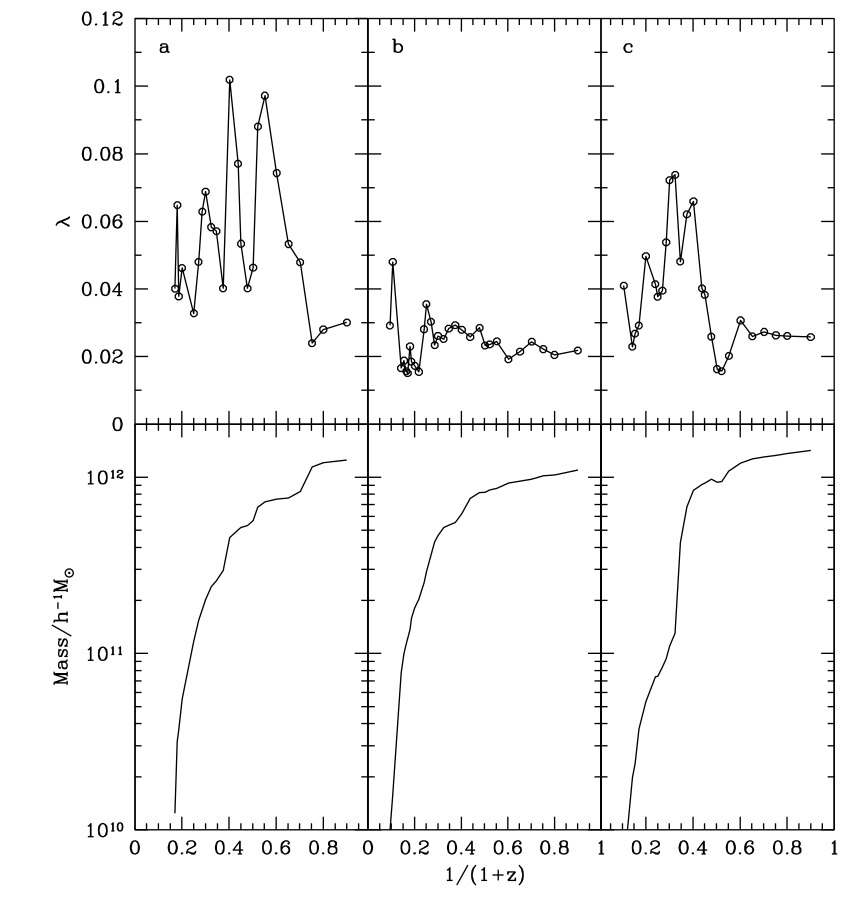
Galaxy formation: the biased point of view of the spin
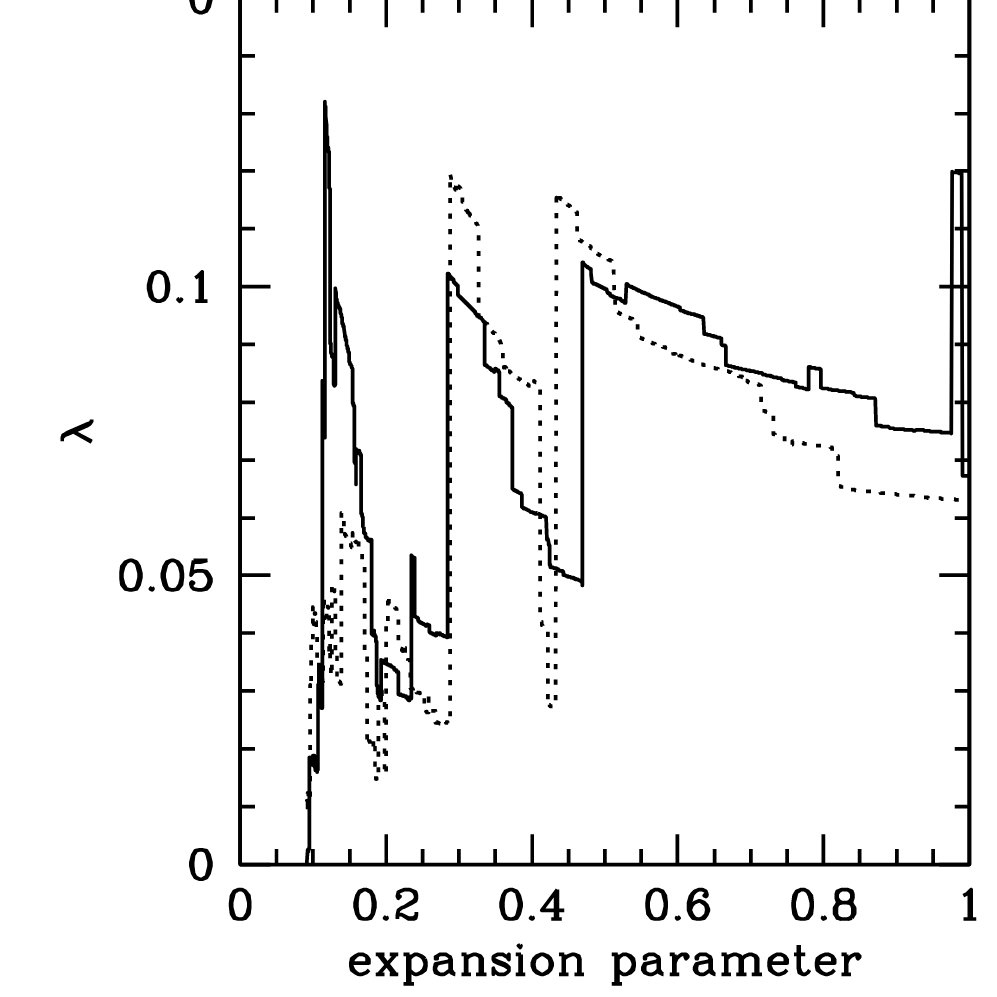
Stochastic spin: Vitviska+ 02, Beson+ 20
Spin prediction, Porciani+ 02
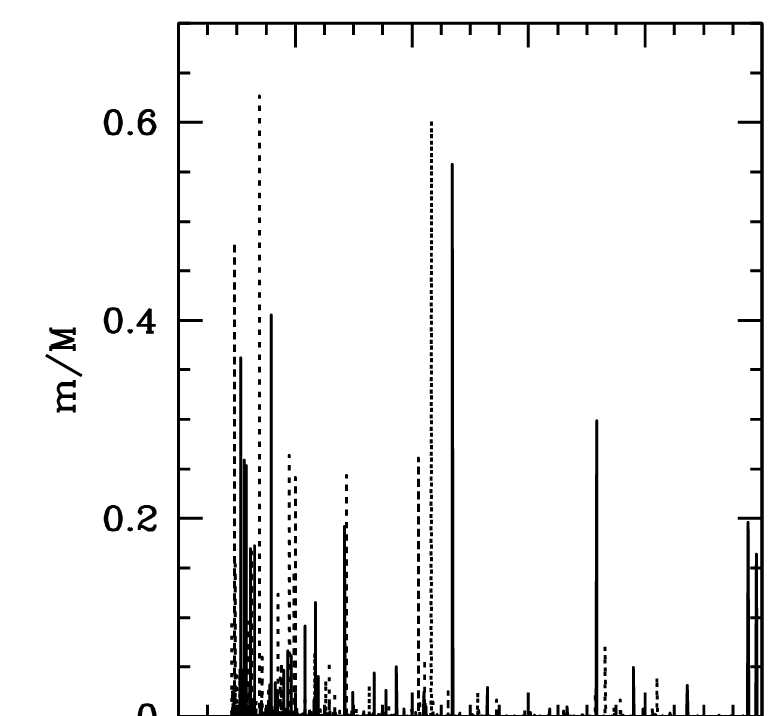
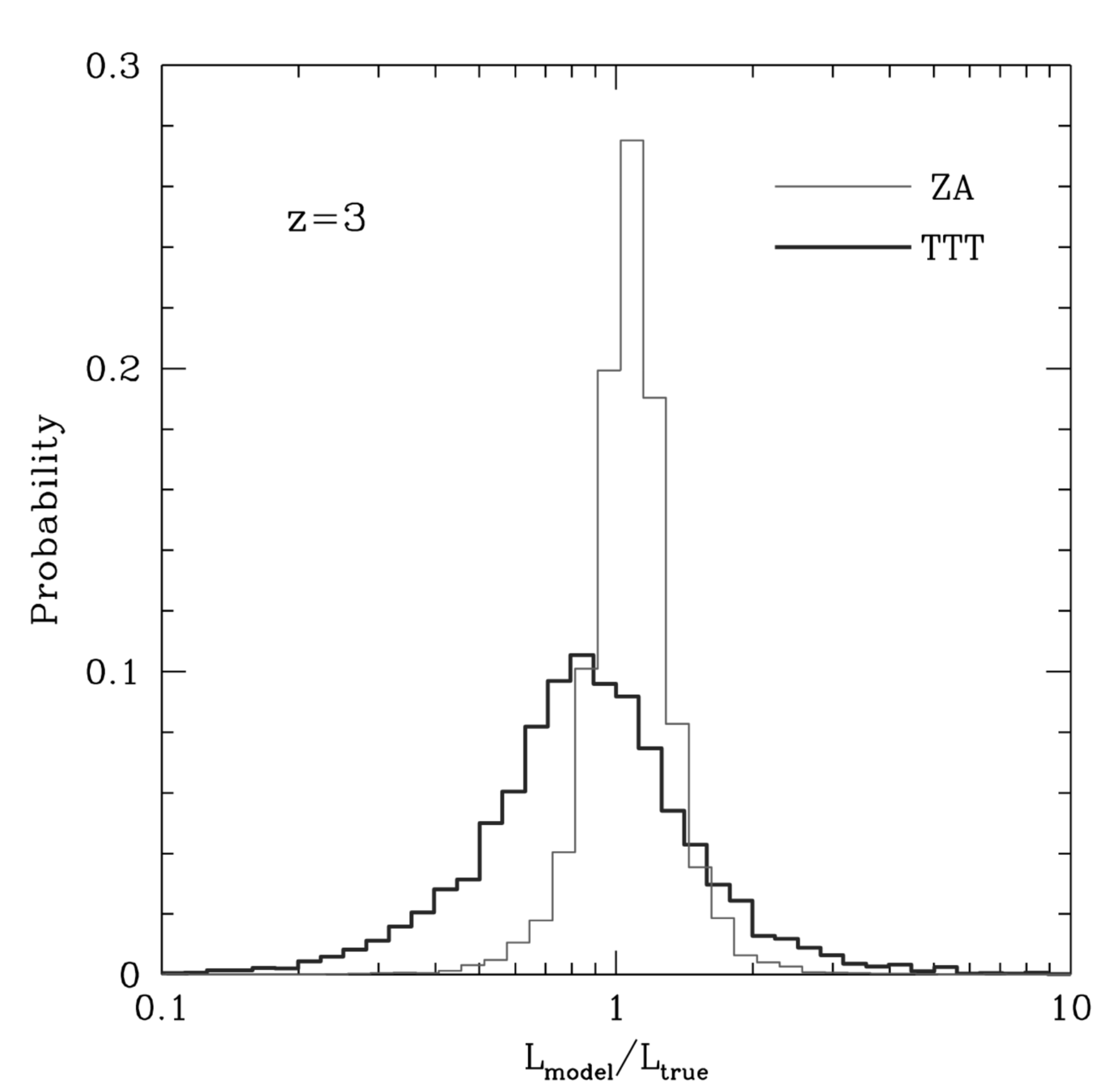
Spin: \[\lambda = \dfrac{j}{\sqrt{2}R_\mathrm{vir}V_{vir}}\]
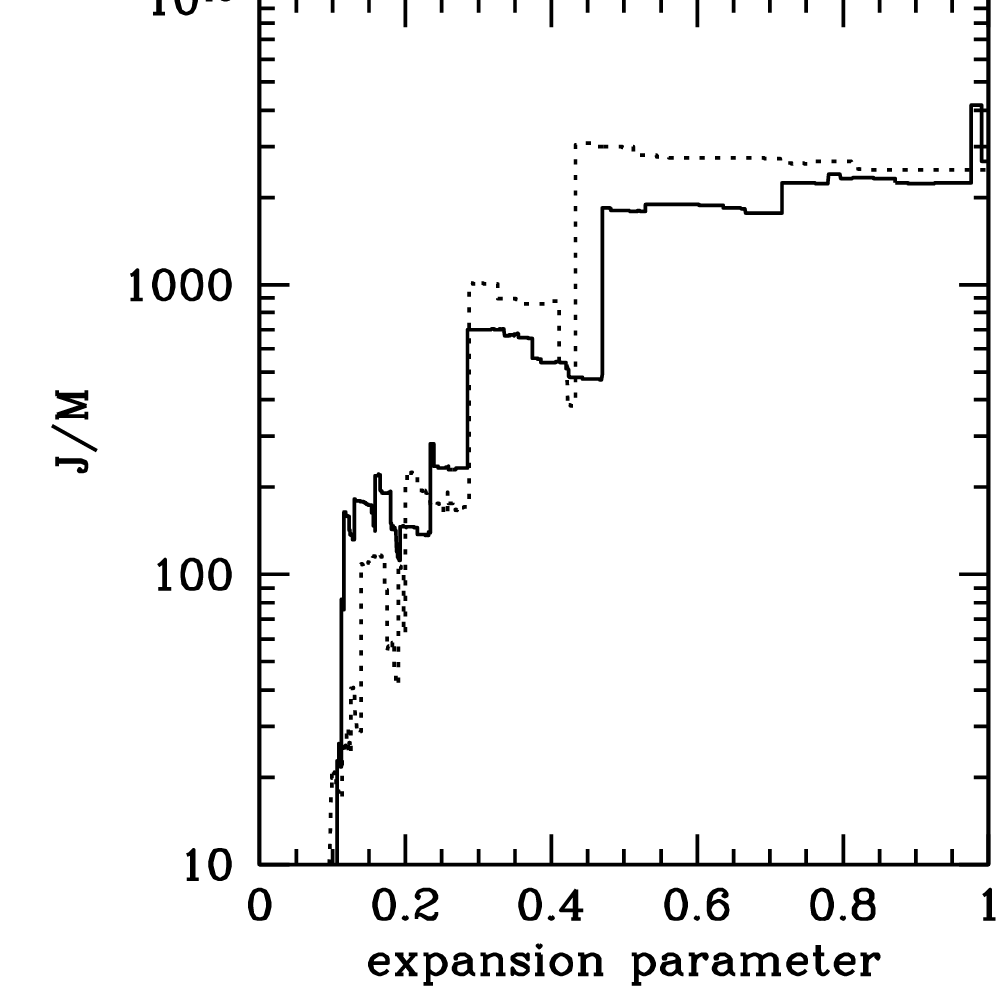
- Spin jumps at mergers
- Distribution well reproduced by drawing mergers' parameters randomly
- Theoretical predictions are, at best, inaccurate
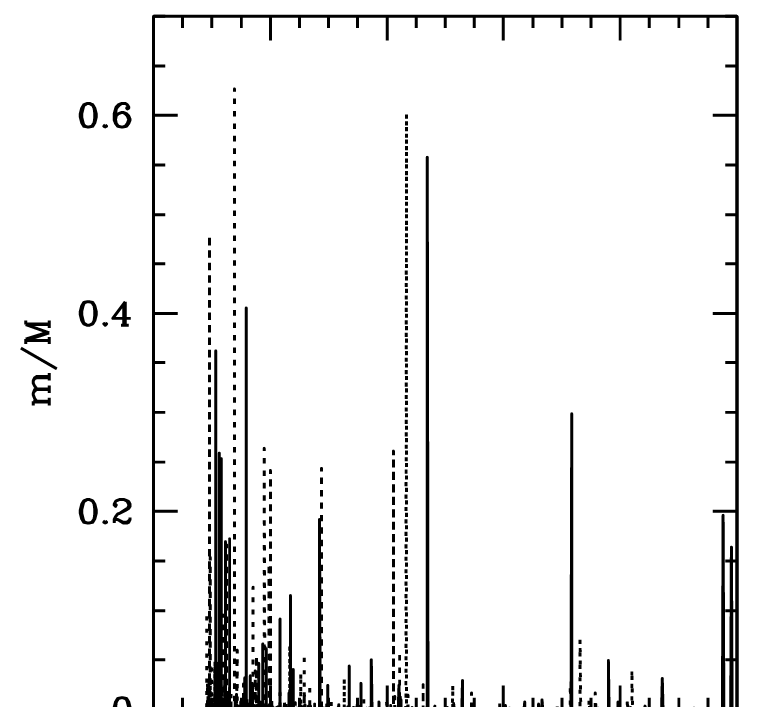
First complication
\(1\,\mathrm{dex}\)!
“Mergers bring chaos”
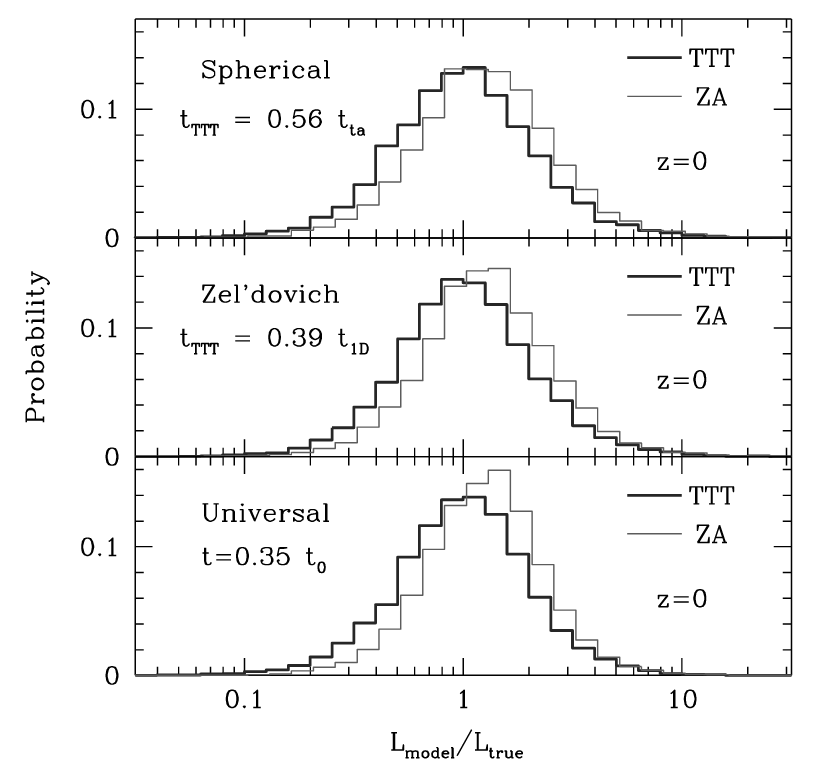
Second complication
Let's be optimistic and assume we can predict DM spin
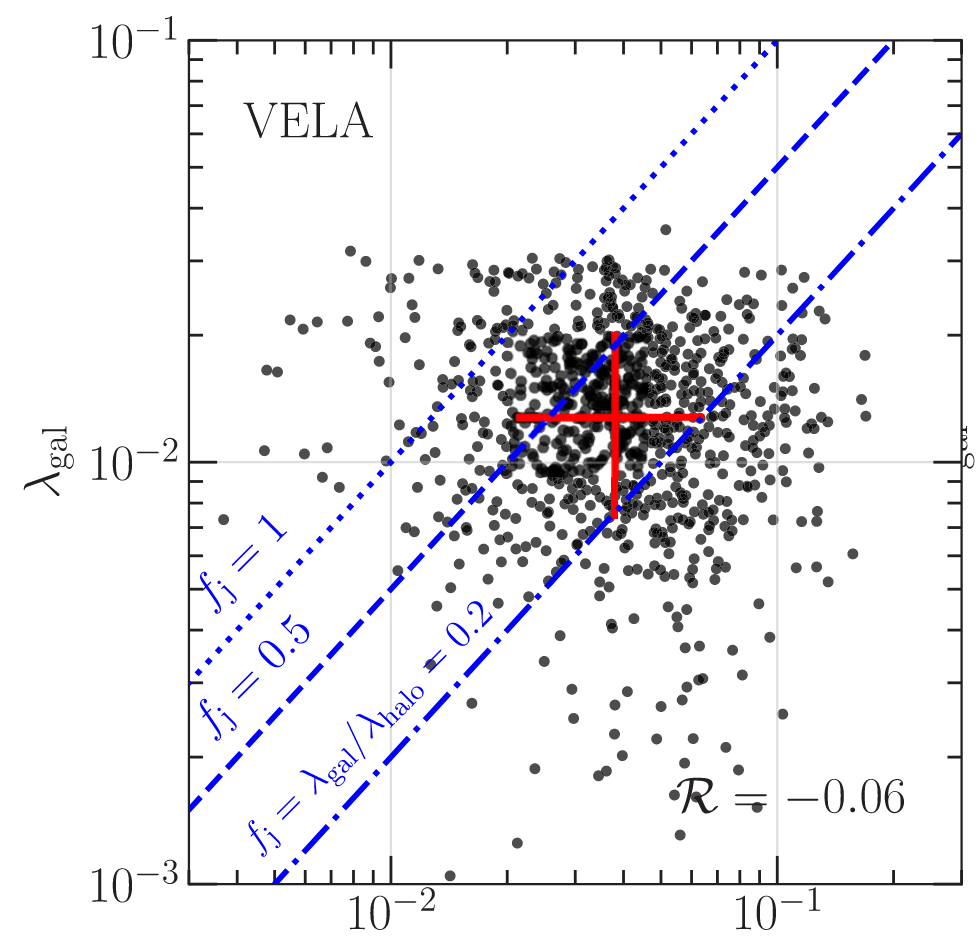
DM spin is not even a good predictor for the galaxy's!
TR: Jiang+ 19, BL: Rodriguez-Gomez+ 22
\(\lambda_\mathrm{DM}\)

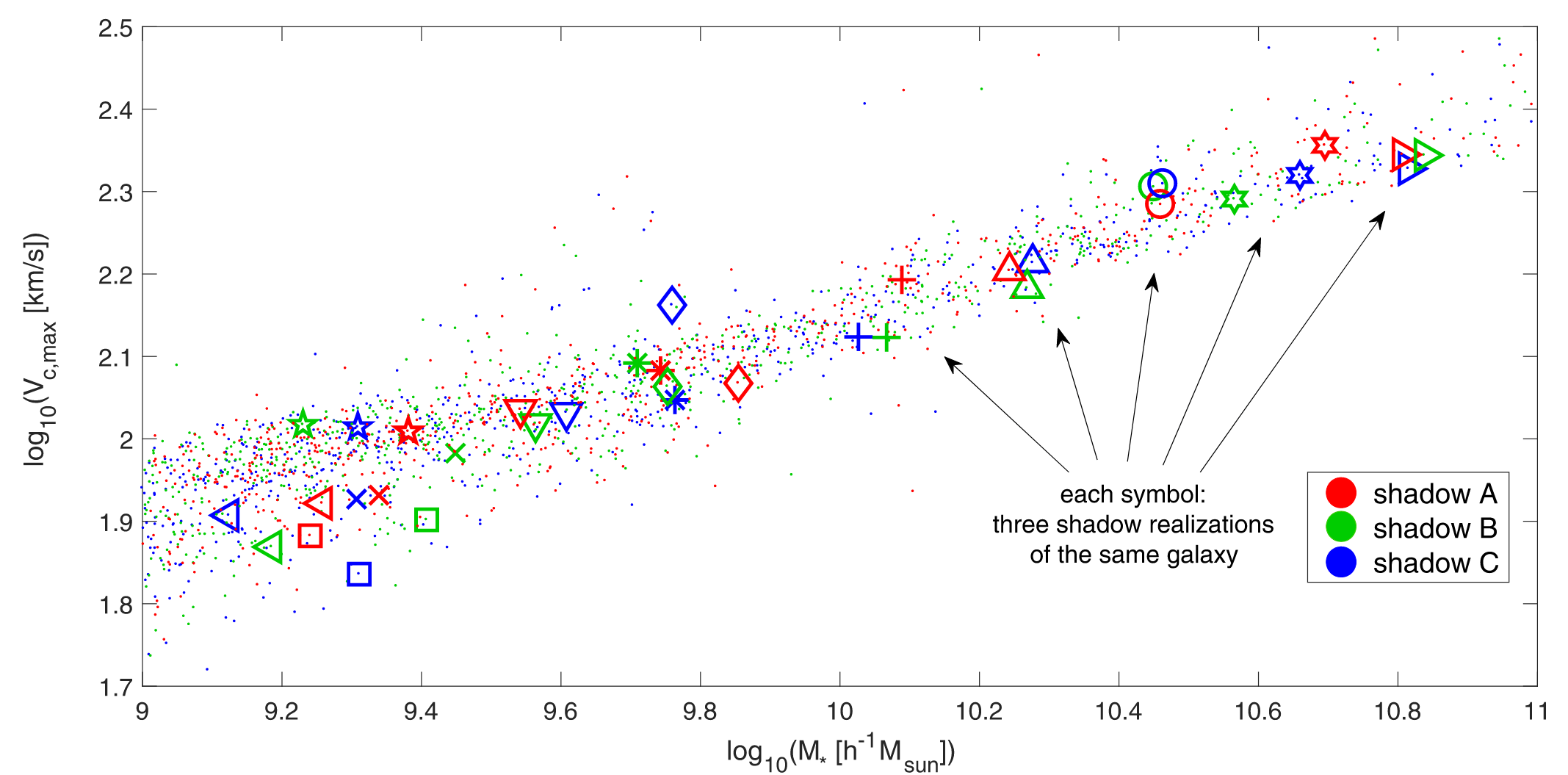
Butterfly effect: Genel+ 19, see also Thiébaut+ 08
Third complication
Resimulating the same galaxy twice yields different results ⇒ galaxies are chaotic
But are galaxies truly chaotic?
How complex are galaxies?
Results from Cadiou+ 24a
1
How complex are galaxies?
Results from Cadiou+ 24a
1

Example of the S-curve:
2D manifold embedded in 3D

Compute \(k\)-nearest neighbors
→ edges of a graph

Draw a point
→ find shortest path to all others

Take a radius
count number of points, \(p\) within \([r, r+\mathrm{d} r]\)
\(\Rightarrow p(r) \propto r^{D-1}\)
\(r\)
\(\#(<r)\)
Actually \(p(r)\propto \sin^{D-1}(r)\), Granata & Carnevalle 16

\(\#(<r)\)

COSMOS dataset
300,000 observed galaxies
Horizon-AGN
700,000 simulated galaxies
We have a method to measure
the intrinsic dimensionality of any dataset.
- Magnitude measurements (not images!)
- 14 photometric wide-bands (u*, g, r, i, z, y, Y, J, H, Ks, B, V, IRAC CH1 & CH2)
+ 14 narrow-bands - SNR > 2
- passive/active selection
Note: we are not working with images, but integrated magnitudes


COSMOS dataset
300,000 observed galaxies
Horizon-AGN
700,000 simulated galaxies
No more than \(\sim 4\) independent parameters? (with comparable magnitudes)
See Disney 08 for even more controversial results, although with smaller statistics
Horizon-AGN
700,000 simulated galaxies
No more than \(\sim 3\) independent parameters!
Galaxy formation is tightly constrained
Galaxies populate a 3D attractor?
\(M\)
\(z\)
\(j\)


With simulated noise
Without simulated noise
Is DM angular momentum chaotic?
Results from Cadiou+21, 22
2
Is DM angular momentum chaotic?
Results from Cadiou+21, 22
2

DM angular momentum



\(z=0\)
\( z = 100\)



\(z=0\)
\( z = 100\)
[White 84]

DM angular momentum



\(z=0\)
\( z = 100\)
[Genetic modifications: Roth+16, see also Rey&Pontzen 18, Stopyra+20]

DM angular momentum










Time
Angular
momentum
DM angular momentum
✅ AM of fixed DM regions responds ~linearly (so is not chaotic!)
However, particle membership hence DM halo does not

Angular
momentum
Time
DM angular momentum
Halo AM is hard to predict
the usual culprit are mergers
Are mergers really
stochastic?
Results from Cadiou +24b
3

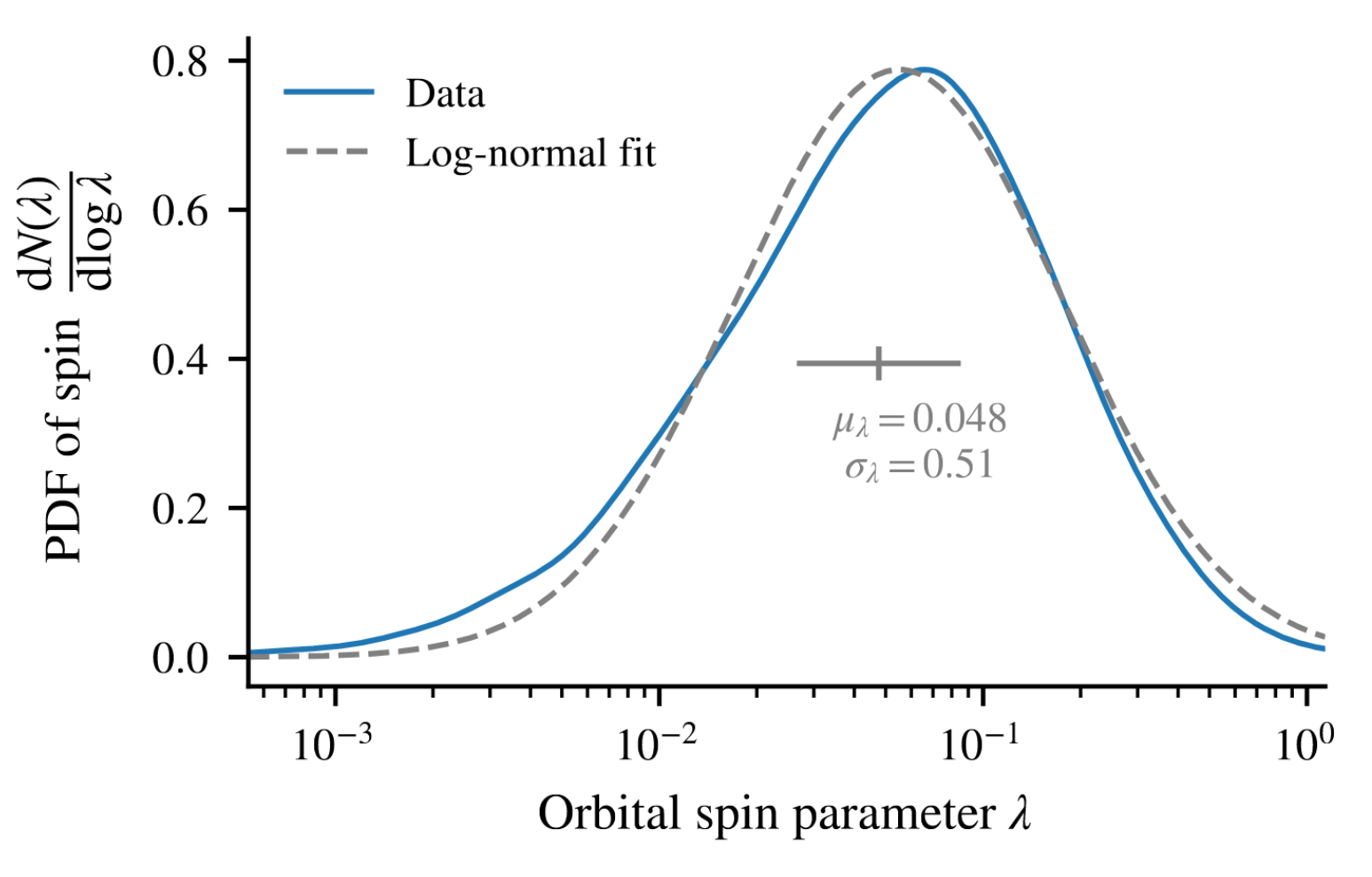
Based on the critical event theory (Cadiou +20)
We can make some reasonable predictions
of orbital spin of mergers
Given: tides + density peaks



Changes to tides at \(z=100\), effect at \(z<1\)
tides ×0.5 ⇒ merger @ \(z=0.7\)
tides ×1.1 ⇒ merger @ \(z=0.55\)
tides ×1.2 ⇒ merger @ \(z=0.5\)
tides ×2 ⇒ merger @ \(z=0.2\)
How chaotic is baryonic
angular momentum?
Results from Cadiou +21a
4
How chaotic is baryonic
angular momentum?
Results from Cadiou +21a
4


Full hydro simulations
(RAMSES, New-Horizon model):
- Resolved disk height
\(\Delta x_\mathrm{min} = 35\ \mathrm{pc}\) - \(M_\mathrm{200c} = 10^{12}\ \mathrm{M}_\odot\)
at \(z=2\) - SF, AGN, SN feedback
- 3 galaxies, 5× scenario each
\( j_0 \times 0.66\)
\( j_0 \times 0.8\)
\( j_0 \times 1.2\)
\( j_0 \times 1.5\)
\( j_0 \times 0.66\)
\( j_0 \times 0.8\)
\( j_0 \times 1.2\)
\( j_0 \times 1.5\)
\( j_0 \times 0.66\)
\( j_0 \times 0.8\)
See Cadiou+21a
INPUT: Changes to tides \(z=\infty\)
OUTPUT: Ang. mom
\(z=2\)


\( j_0 \times 0.66\)
\( j_0 \times 0.8\)
\( j_0 \times 1.2\)
\( j_0 \times 1.5\)
\( j_0 \times 0.8\)
See Cadiou+21a
INPUT: Changes to tides \(z=\infty\)
OUTPUT: Ang. mom
\(z=2\)

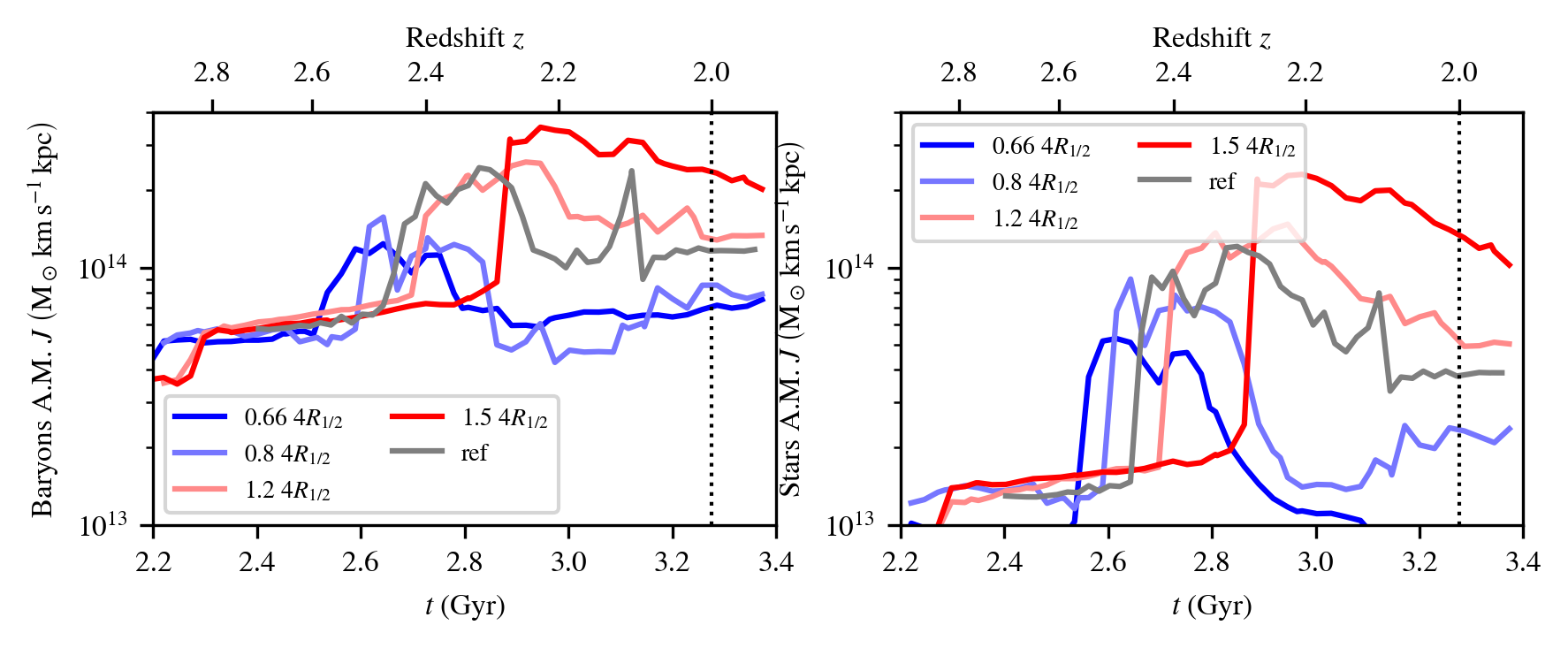
Stellar angular momentum responds ~linearly
to large-scale tides

Gas + stars spAM
Stars spAM
Halo spAM
Halo spAM
See Cadiou+21a
Halo and disk evolve separately,
this allows stellar AM to be ~linear despite halo AM not being

Gas + stars spAM
Stars spAM
Halo spAM
Halo spAM
See Cadiou+21a

Special case: no massive satellite
Low tides
High tides
\(\mathcal{B}\searrow\)
\(R_\mathrm{eff} \nearrow \)
\(v/\sigma\nearrow\)
See Cadiou+21a
Impact of the cosmological-scale density on halo properties
Results from Cadiou +21b
5





What if the galaxy had formed here instead?




What if the galaxy had formed here instead?


or here?
The “splicing” technique


- Generate ICs
- Integrate (\(N\)-body)
- Select region of interest
- Trace back to ICs
- “Splice” the density
- Integrate again

\(t\)

Splicing: equivalent of constraining density field at all points in region
\(\longleftarrow 50\,\mathrm{Mpc} \longrightarrow\)
Splicing in 1D





Splicing in 1D


Most likely field \(f\) with
- same value in spliced region (\(a\)),
- as close as possible outside (\(b\))



Mathematically, \({\color{green}f}\) is the unique solution that satisfies:
- \( {\color{green}f(x)}= {\color{blue}a(x)},\qquad\qquad\qquad\forall x \in\Gamma\)
- minimizes \[\mathcal{Q} = ({\color{red}b}-{\color{green}f})^\dagger\mathbf{C}^{-1}({\color{red}b}-{\color{green}f}),\quad \forall x \not\in \Gamma \]
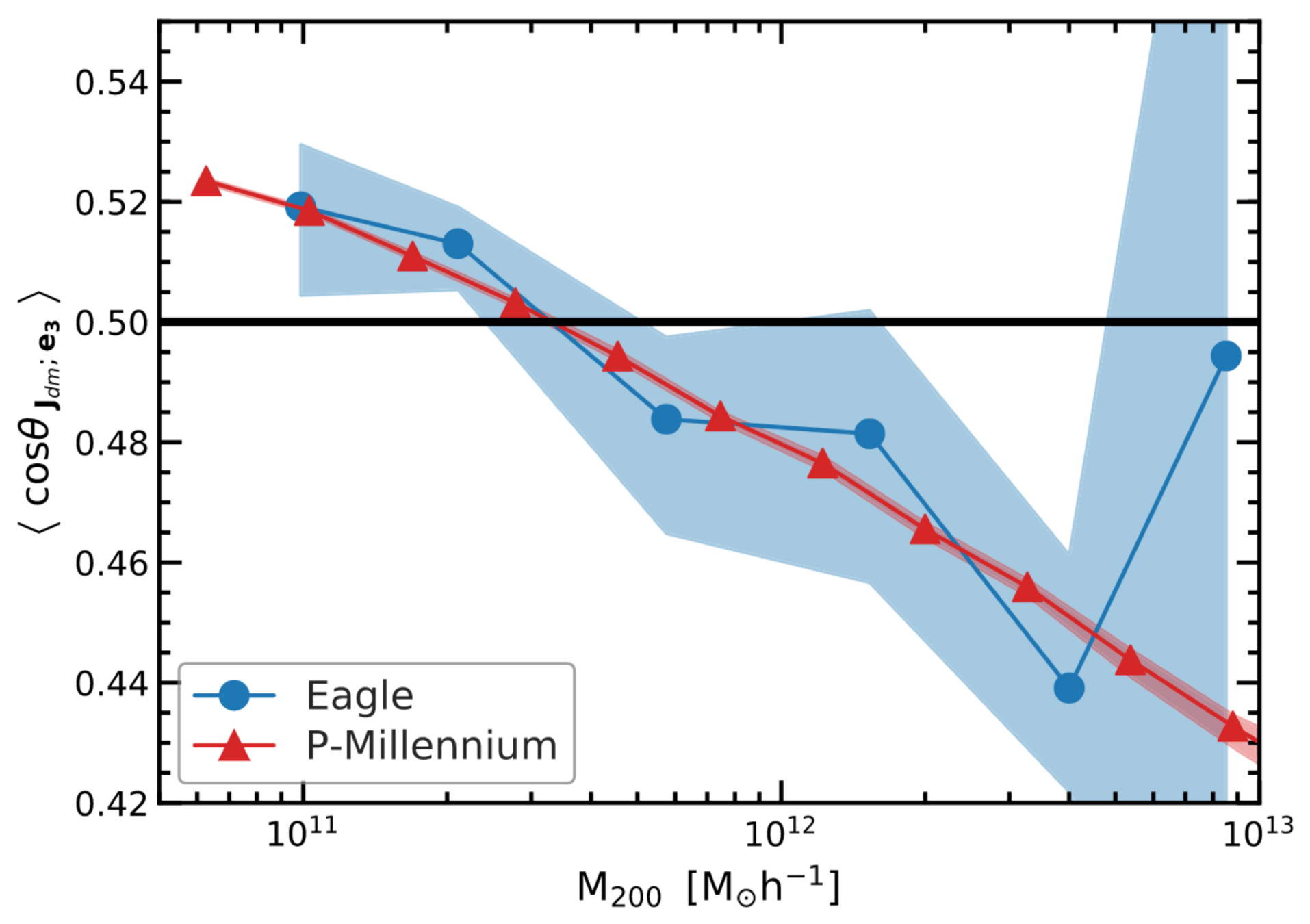
The causal origin of DM halo concentration


\(M^{(1)}_{200\mathrm{c}}, c^{(1)}_\mathrm{NFW}, \dots\)


\(M^{(2)}_{200\mathrm{c}}, c^{(2)}_\mathrm{NFW}, \dots\)


\(M^{(\dots)}_{200\mathrm{c}}, c^{(\dots)}_\mathrm{NFW}, \dots\)


\(M^{(10)}_{200\mathrm{c}}, c^{(10)}_\mathrm{NFW}, \dots\)
Same halo in 10× different environments
Repeat experiment for 7 halos (70 realisations in total)
Same halo in 10× different environments
Repeat experiment for 7 halos (70 realisations in total)


\(M^{(1)}_{200\mathrm{c}}, c^{(1)}_\mathrm{NFW}, \dots\)


\(M^{(2)}_{200\mathrm{c}}, c^{(2)}_\mathrm{NFW}, \dots\)


\(M^{(\dots)}_{200\mathrm{c}}, c^{(\dots)}_\mathrm{NFW}, \dots\)


\(M^{(10)}_{200\mathrm{c}}, c^{(10)}_\mathrm{NFW}, \dots\)

The causal origin of DM halo concentration
Same halo in 10× different environments
Repeat experiment for 7 halos (70 realisations in total)


\(M^{(1)}_{200\mathrm{c}}, c^{(1)}_\mathrm{NFW}, \dots\)


\(M^{(2)}_{200\mathrm{c}}, c^{(2)}_\mathrm{NFW}, \dots\)


\(M^{(\dots)}_{200\mathrm{c}}, c^{(\dots)}_\mathrm{NFW}, \dots\)


\(M^{(10)}_{200\mathrm{c}}, c^{(10)}_\mathrm{NFW}, \dots\)


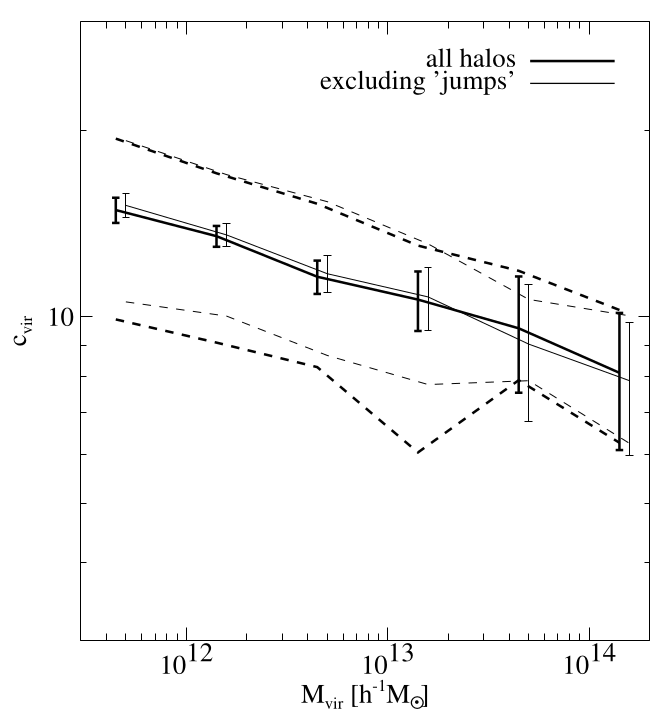
The causal origin of DM halo concentration
50% of population
Impact of the cosmological-scale tides on halo properties
Results from Storck, Cadiou in prep.
6

Impact of the cosmological-scale tides on halo properties
Results from Storck, Cadiou in prep.
6
\(\rho_\mathrm{i}, v_\mathrm{i}\)
\(\Lambda\)CDM+baryon non-linear evolution
halo & galaxy properties
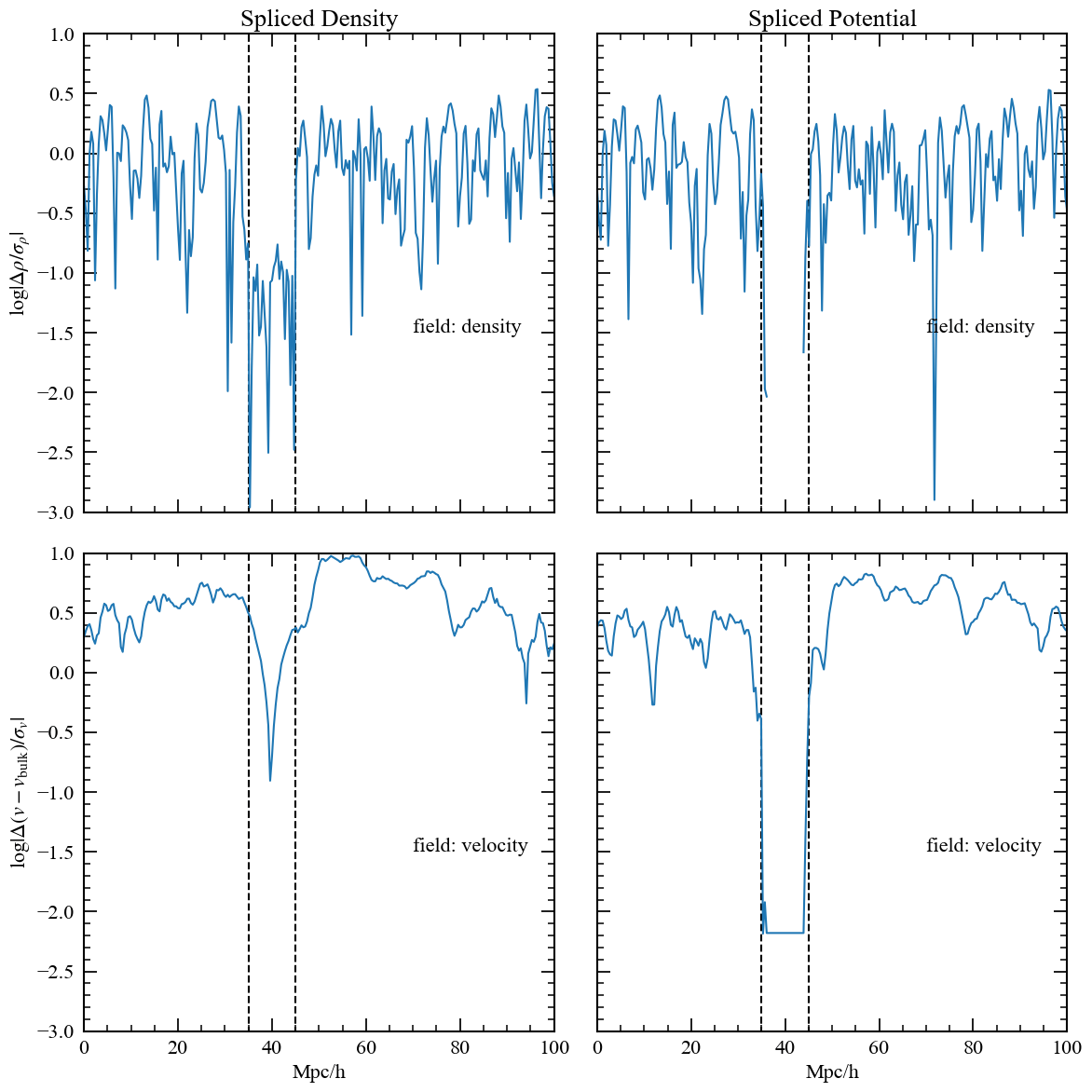


\(\log\left|\dfrac{{\color{blue}\rho_\mathrm{i}} - \color{red}\rho_\mathrm{i}}{\sigma_\rho}\right|\)
\(\log\left|\dfrac{{\color{blue}v_\mathrm{i}} - \color{red}v_\mathrm{i}}{\sigma_v}\right|\)

Issue : splicing the density does not fix the velocity & tides




Issue : splicing the density does not fix the velocity & tides
Solution: splice the potential
\(\log\left|\dfrac{{\color{blue}\rho_\mathrm{i}} - \color{red}\rho_\mathrm{i}}{\sigma_\rho}\right|\)
\(\log\left|\dfrac{{\color{blue}v_\mathrm{i}} - \color{red}v_\mathrm{i}}{\sigma_v}\right|\)
Remember \(\nabla^2\phi = 4\pi G\rho\) so
\[\rho_n\propto\frac{\phi_{n+1}-2\phi_n+\phi_{n-1}}{\Delta x^2}\]
\[v_n\propto\frac{\phi_{n+1}-\phi_{n-1}}{2\Delta x}\]


Same halo (same initial tides + density)
forming closer and closer to filament

Repeat for 5 halos, 9 positions



Variation compared to mean value
For different quantities
spin alignment
shape alignment
Conclusions
The title might have been clickbait… but
-
On global scales galaxies aren't that complex: success of simulations
Actual complexity is on the order of 3 (mass, redshift, SFR?)
-
Tides determine merger orbital parameters & angular momentum accretion
Mergers are not stochastic/not rerolling the dice
-
Trickling down to galactic scale, which drives scaling relations
Galaxies are less stochastic than expected
Galaxy & DM spin sins are partially independent at the level of individual galaxies
-
Non-linear effects on halo shape and alignment are comparable to population-level
Crucial to investigate further the success of Euclid or LSST
Are galaxies chaotic?


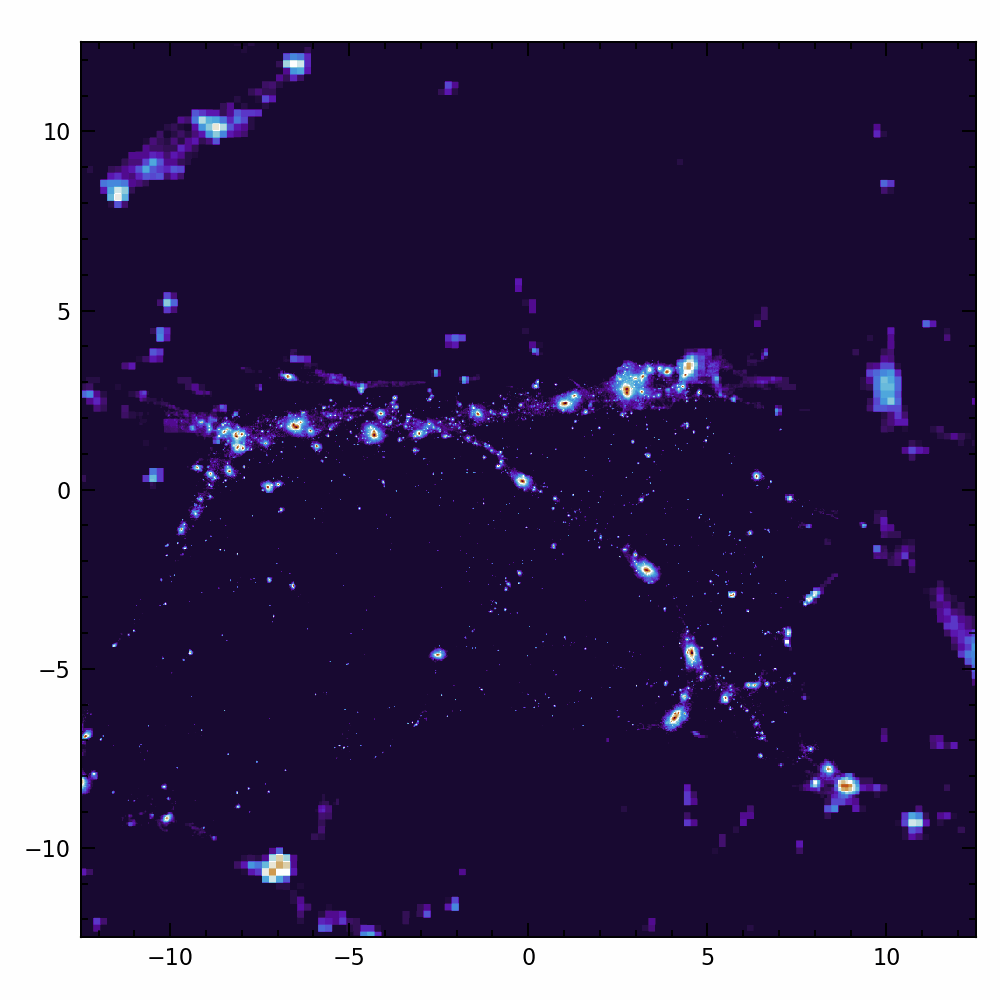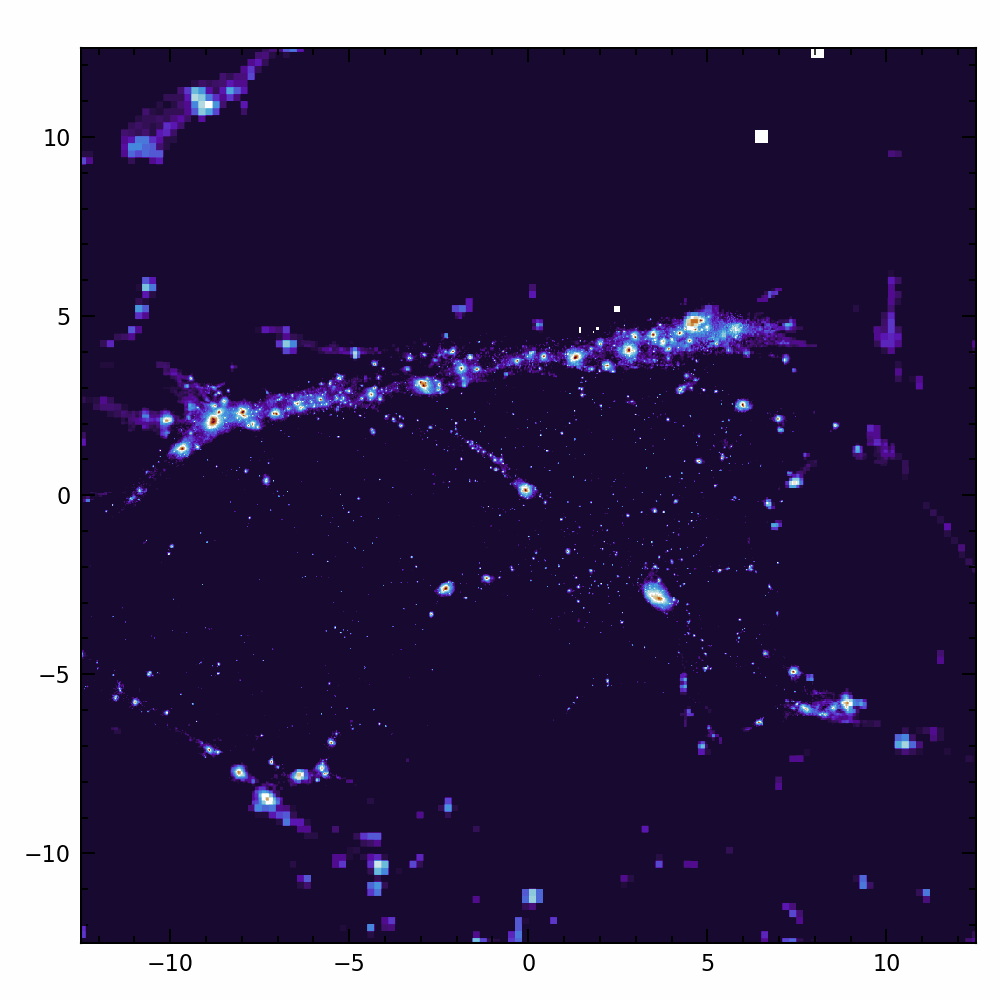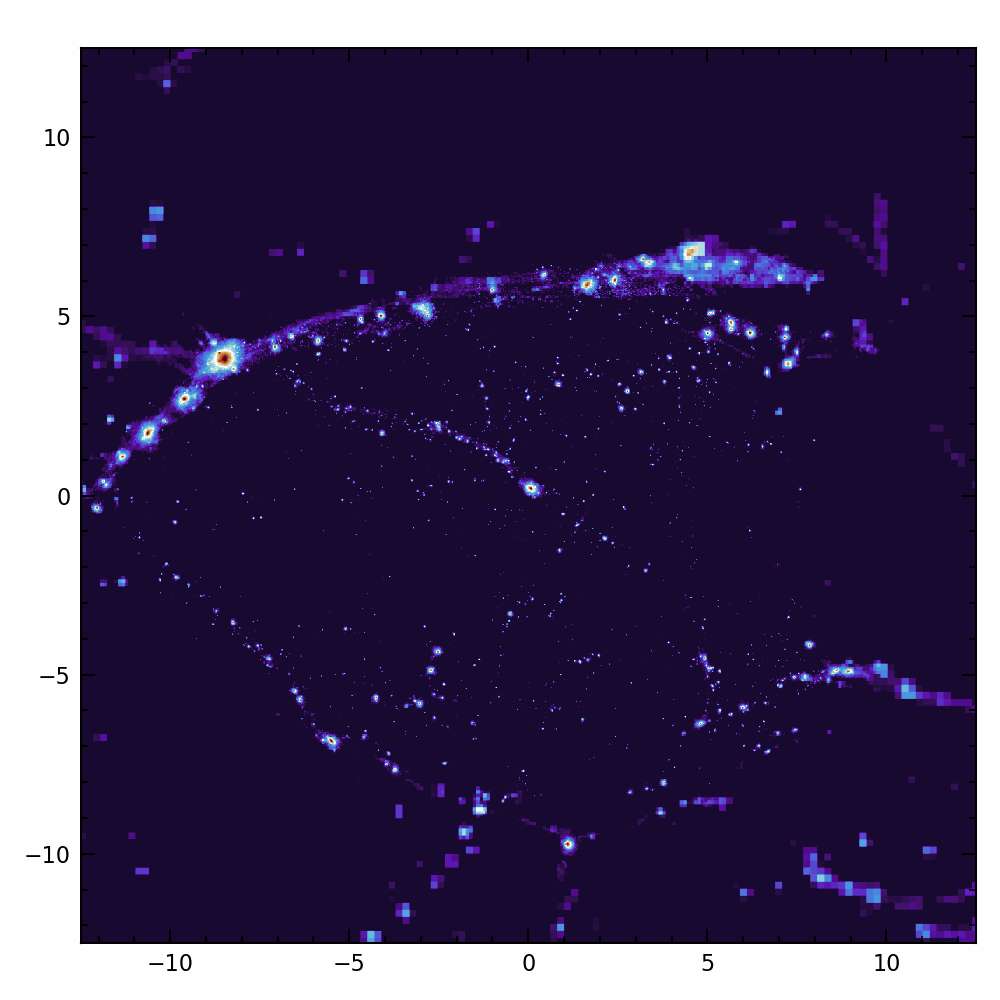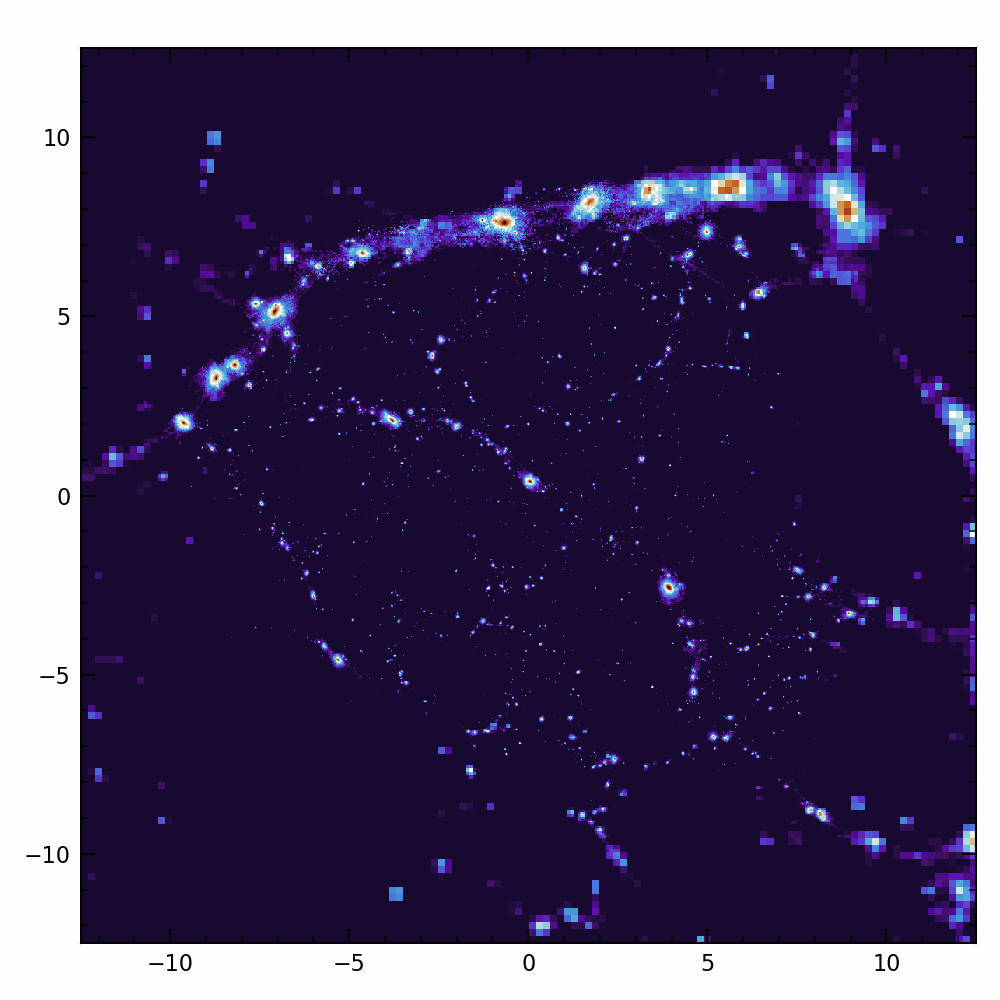

Angular momentum:
- Qualitatively understood
- Abrupt changes with mergers
- Crucial for galaxy formation + weak lensing
Corentin Cadiou
Porciani+02

Vitviska+02, Benson+20

Fall+80
Corentin Cadiou


Vitviska+02, Benson+20

Porciani+02


Fall+80
Angular momentum:
- Qualitatively understood
- Abrupt changes with mergers
- Crucial for galaxy formation + weak lensing
Corentin Cadiou


Fall+80


Vitviska+02, Benson+20

Porciani+02
Angular momentum:
- Qualitatively understood
- Abrupt changes with mergers
- Crucial for galaxy formation + weak lensing
Angular momentum:
- Abrupt changes with mergers
- Qualitatively understood
- Crucial for galaxy formation + weak lensing
Corentin Cadiou


Fall+80


Vitviska+02, Benson+20

Porciani+02
- What's the origin of angular momentum?
- Are mergers truly stochastic?
- How does it translate to galaxy properties?
See Cadiou+21a
based on genetic modifications: Roth+16, Rey&Pontzen 18, Stopyra+20
“Find the most likely \(\Lambda\)CDM realisation
that increases the torques by factor \(f\)”

This is actually done by minimizing \((\delta_\mathrm{new}-\delta_\mathrm{old})^\dagger \textbf{C}^{-1}(\delta_\mathrm{new}-\delta_\mathrm{old})\)
with the constrains \(\tau^{(i)}_\mathrm{new} = f \tau^{(i)}_\mathrm{old}, \quad i=x,y,z\)
MEGATRON simulation
With Rey & Katz
- Large volumes (TNG, HAGN, …)
- statistical results only
- relatively poor resolution
- Small volumes & zoom-ins
- few formation scenarios
- Genetically modified simulations
Large-scale torques control mergers deterministically
which controls secondary galaxy properties
… what happens to the gas?
Corentin Cadiou
Large-scale torques control mergers deterministically
which controls secondary galaxy properties
… what happens to the gas?
Corentin Cadiou

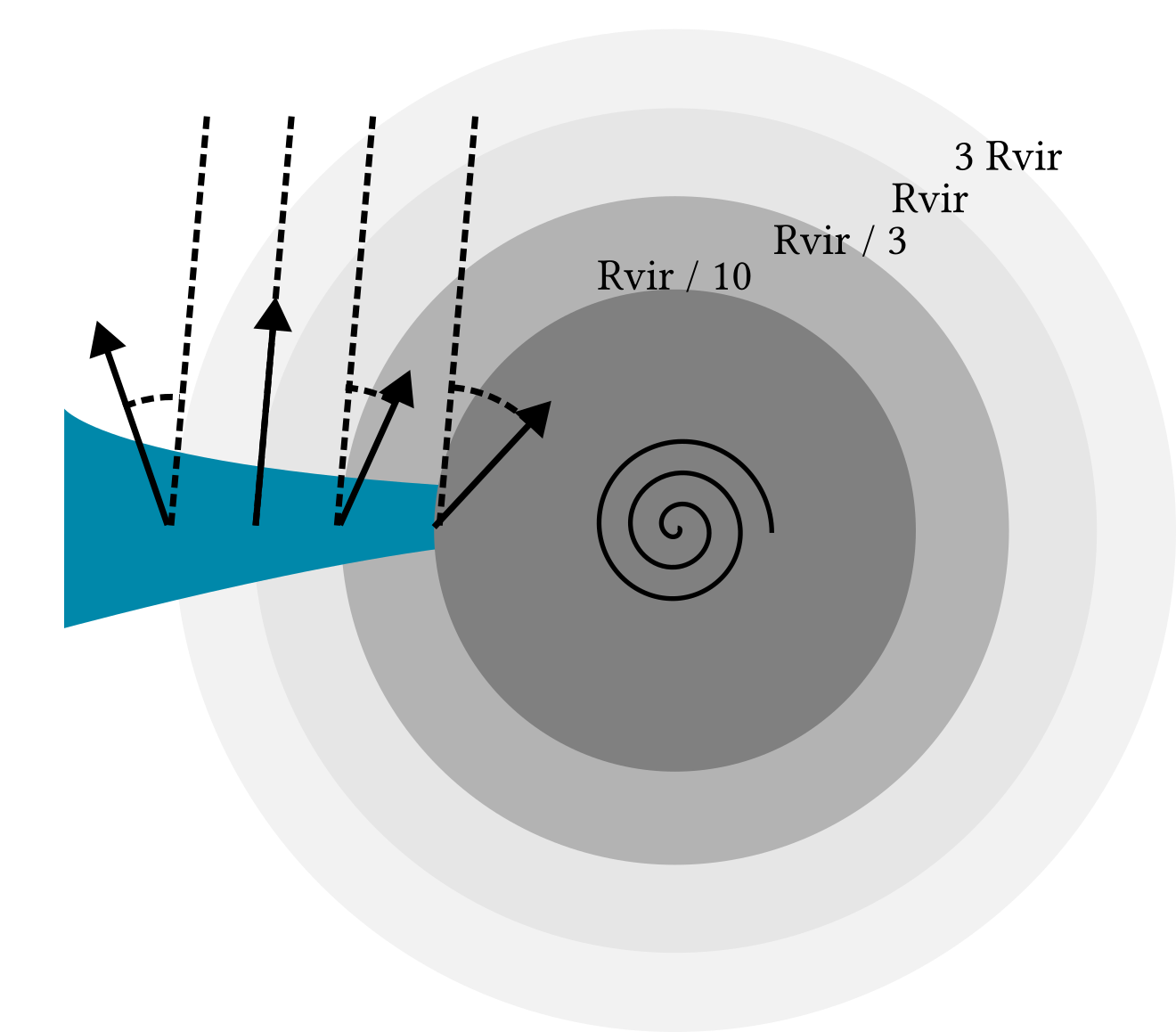
Most of re-alignment happens in the inner CGM \(0.1\leq \displaystyle\frac{r}{R_\mathrm{vir}}\leq 0.3\)
The longer gas remains in inner CGM, the more it realigns (with disk)
Corentin Cadiou
Tracers: Cadiou+19
Cadiou+21b, see also Danovich+15, Prieto+17
Tracking Lagrangian trajectories, comparing \(\vec{j}\) to
\(\parallel\) to direction @ \(R_\mathrm{vir}\)
\(\perp\) to direction @ \(R_\mathrm{vir}\)
⚠️ Only looking at gas that will form stars eventually
Kocjan, Cadiou+24
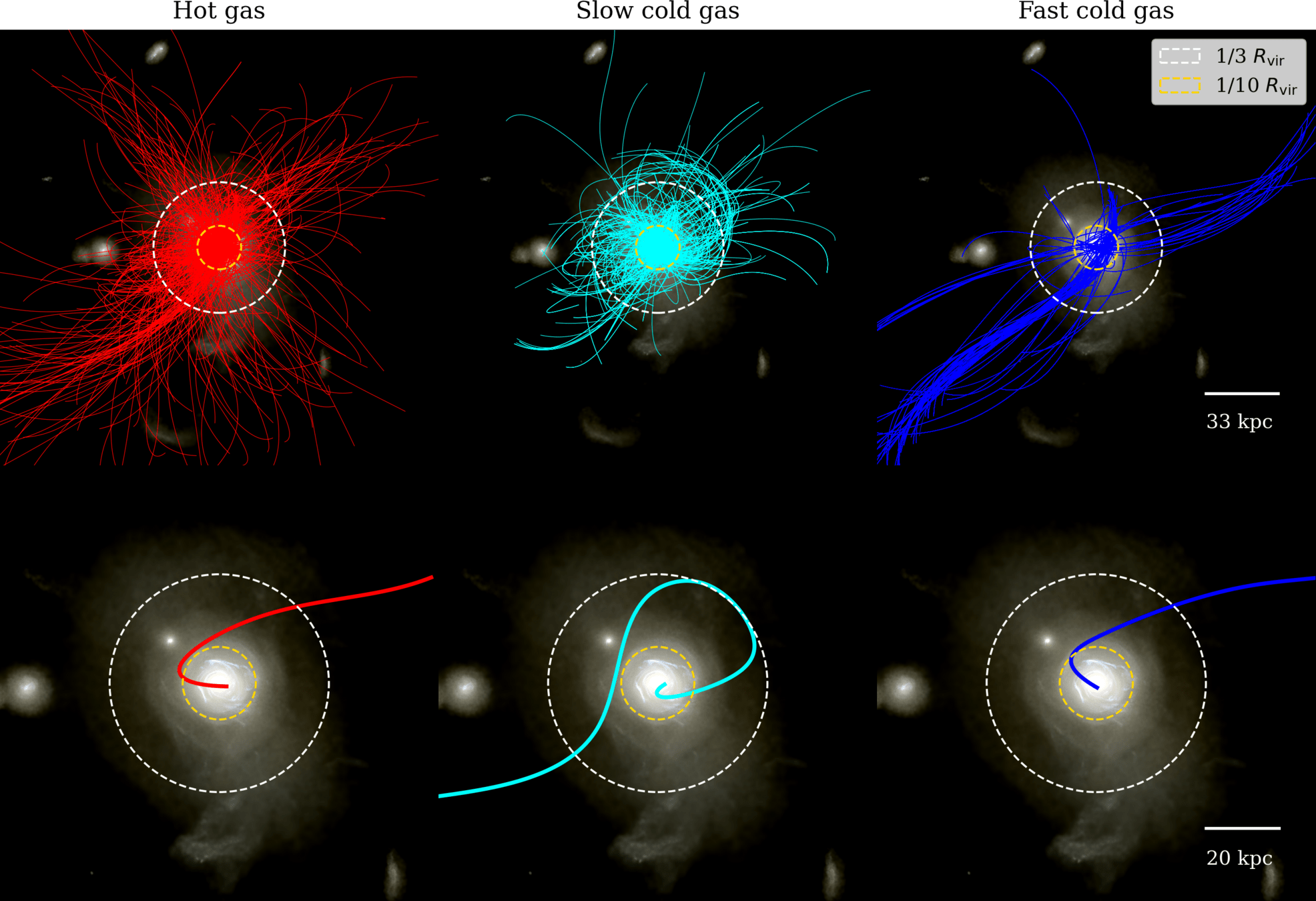

Corentin Cadiou

Time \(2R_\mathrm{vir}\rightarrow R_\mathrm{vir}/3\)
Time \(R_\mathrm{vir}/3 \rightarrow ⭐\)
Angular momentum: bridging galaxy formation to cosmology

2 Spin \(\leftrightarrow\) morphology
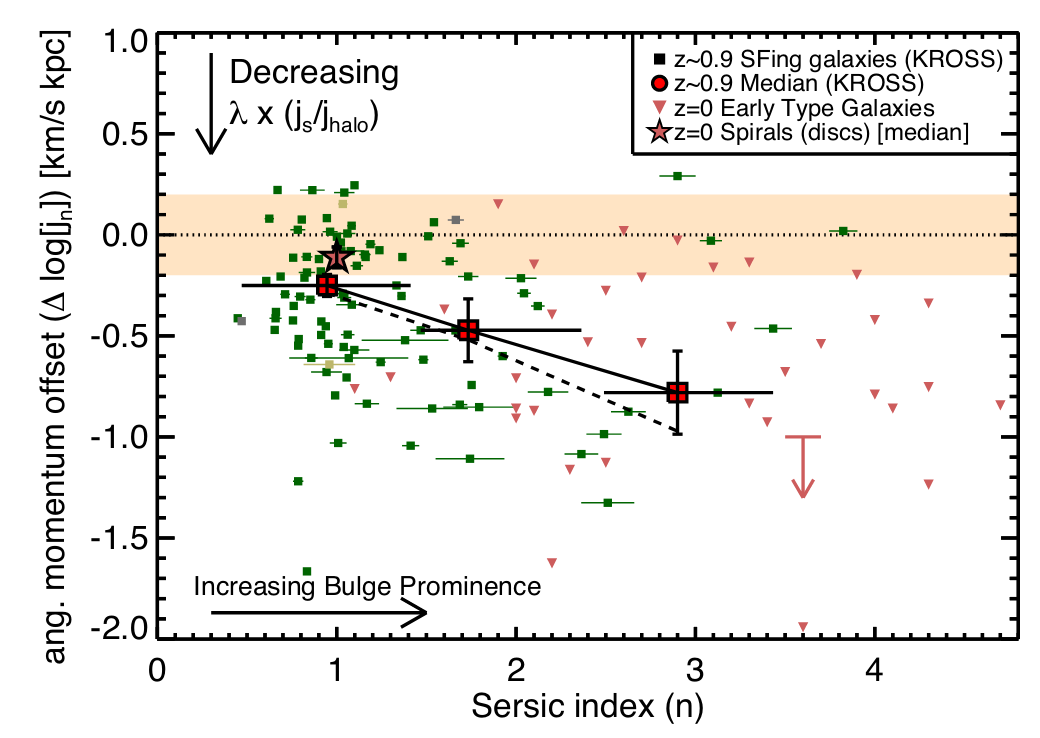
Romanowsky&Fall 12
Harrison+17
Hasan+23 (TNG)
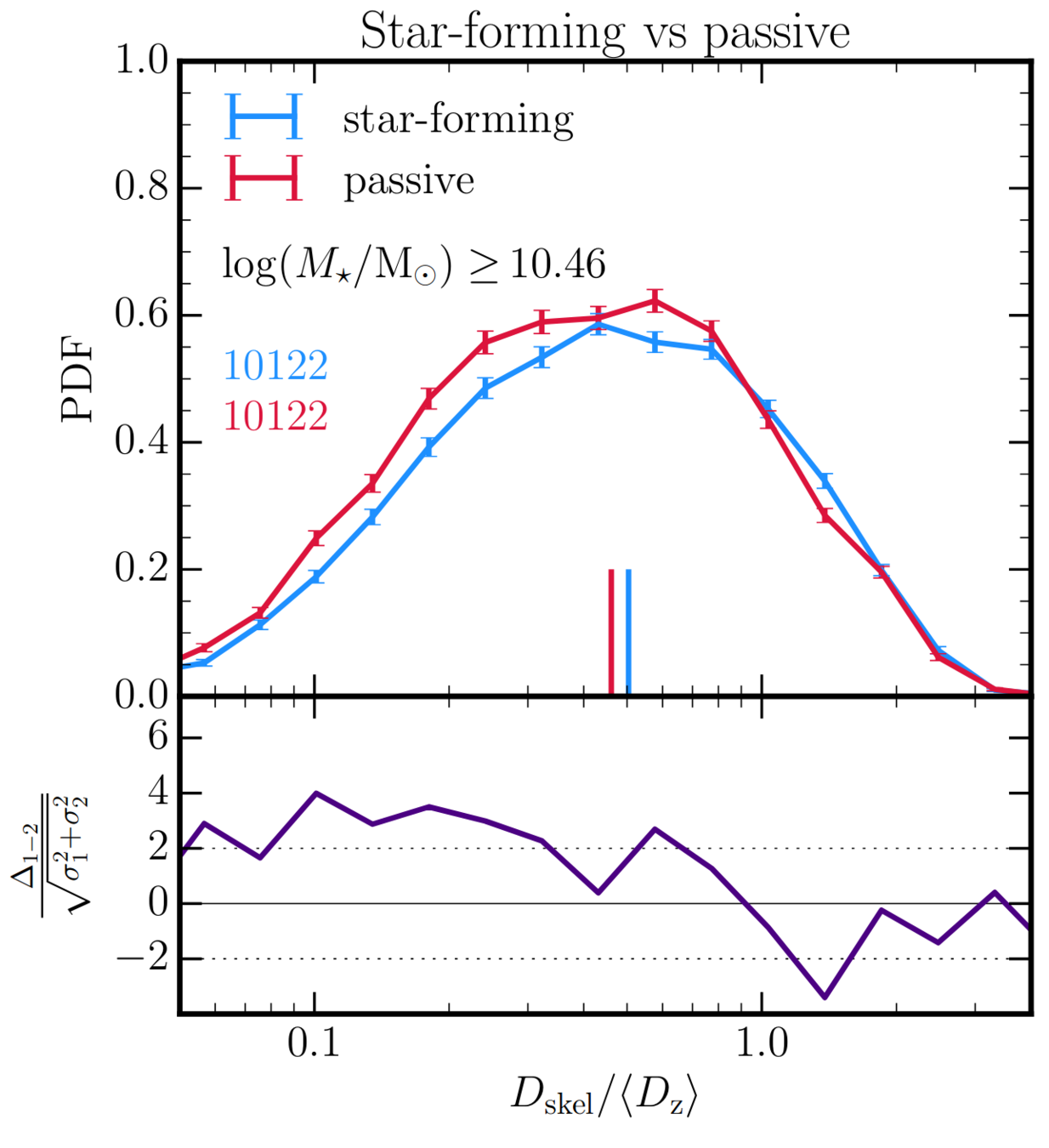
3 Cosmic web \(\leftrightarrow\) SFR
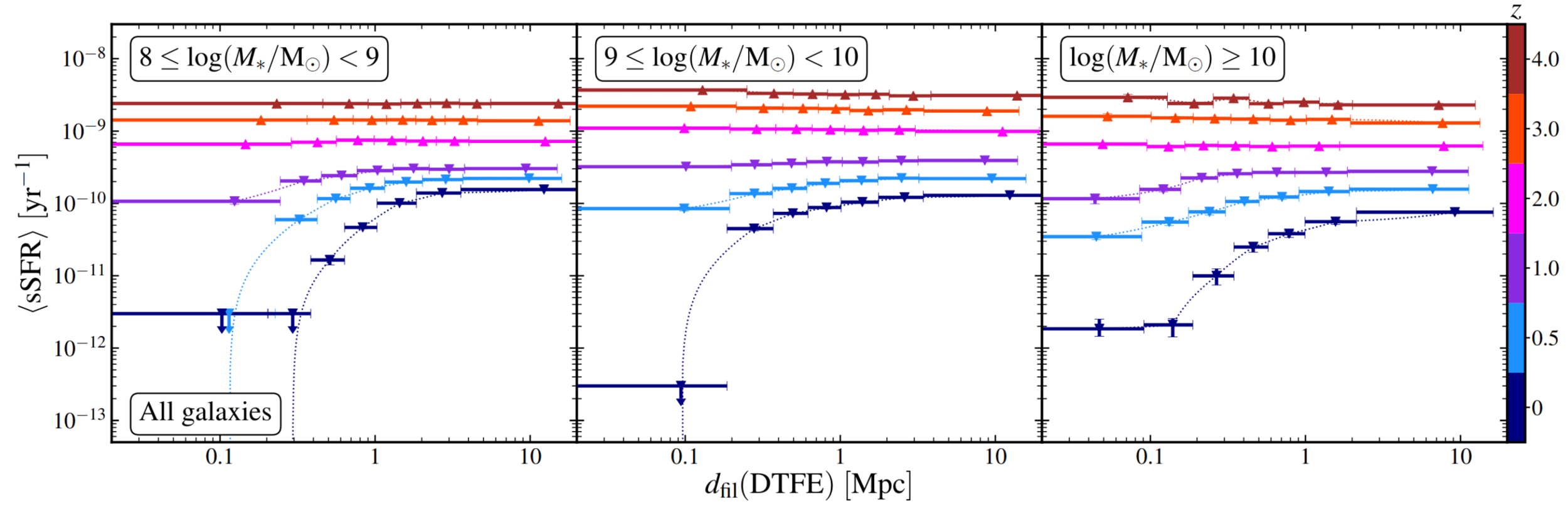

Kraljic+CC+19 (HAGN)
1 Cosmic web \(\leftrightarrow\) spin

1 Cosmic web \(\leftrightarrow\) spin
Ganeshaiah Veena+21
Corentin Cadiou
Angular momentum: bridging galaxy formation to cosmology

2 Spin \(\leftrightarrow\) morphology

Romanowsky&Fall 12
Harrison+17
Hasan+23 (TNG)

3 Cosmic web \(\leftrightarrow\) SFR


Kraljic+CC+19 (HAGN)
1 Cosmic web \(\leftrightarrow\) spin


1 Cosmic web \(\leftrightarrow\) spin
Ganeshaiah Veena+21
Corentin Cadiou
- Why is the effect of the cosmic web at % level?
- What's the arrow of causality?
CW ⇒ spin ⇒ morphology? - How stochastic is galaxy formation?
\(z=0\)
\( z = 100\)
[Genetic modifications: Roth+16, see also Rey&Pontzen 18, Stopyra+20]






Tide \(\nearrow\) delay merger
Tide \(\searrow\) hasten merger
Corentin Cadiou

Corentin Cadiou
Cadiou+21b
So far, I've shown effect of linear perturbations on galaxy formation.
How to probe non-linear couplings?
Corentin Cadiou

Splicing technique Cadiou, Pontzen & Peiris 21
Extended by A. Storck

Corentin Cadiou


Splicing technique Cadiou, Pontzen & Peiris 21
Extended by A. Storck


Corentin Cadiou

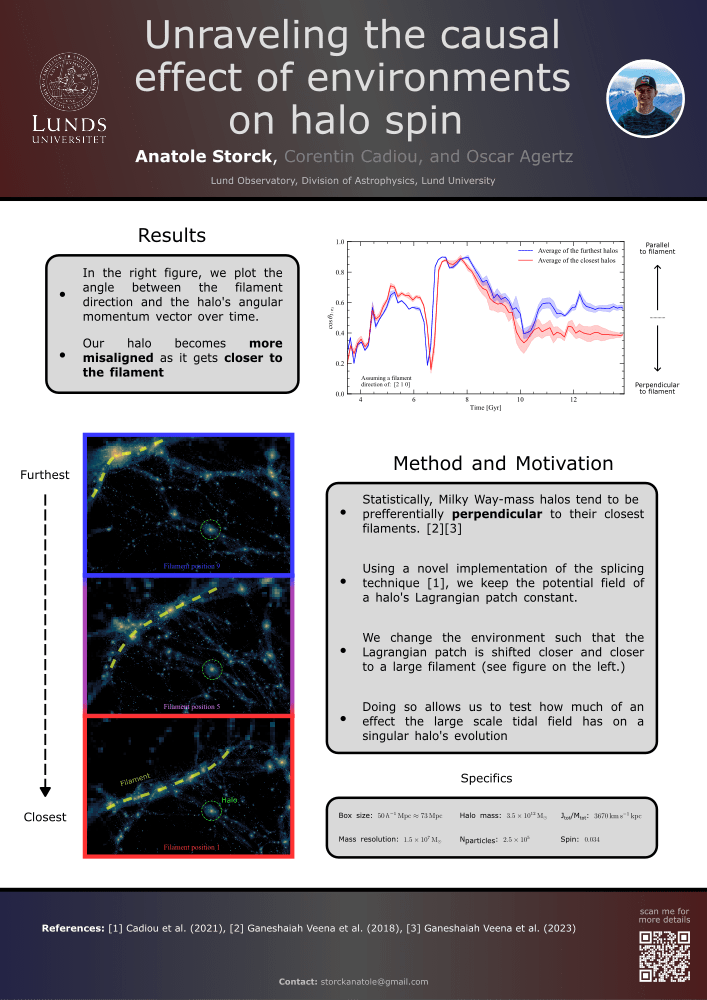


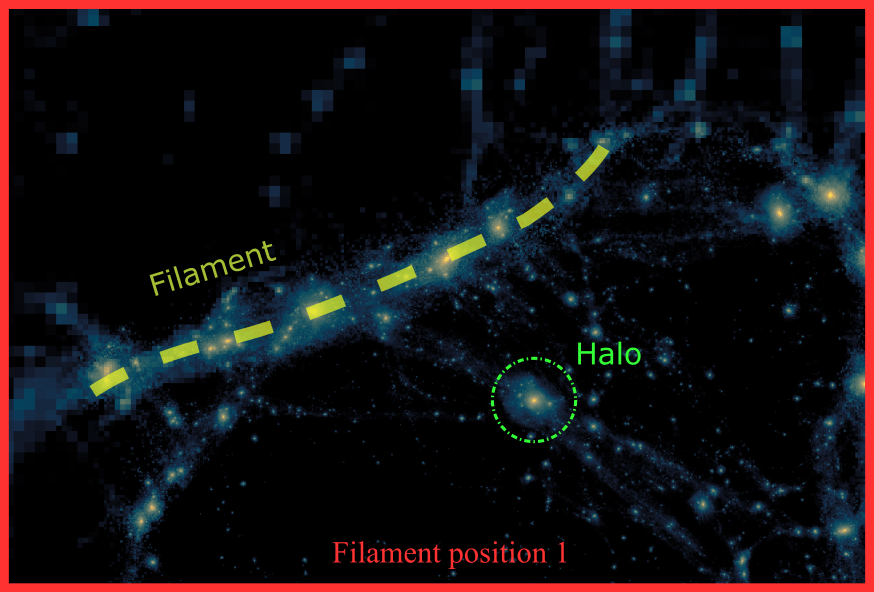
See Anatole Storck's poster for more information!
Far
Close
Halo (mis-)aligns itself to filament
Corentin Cadiou

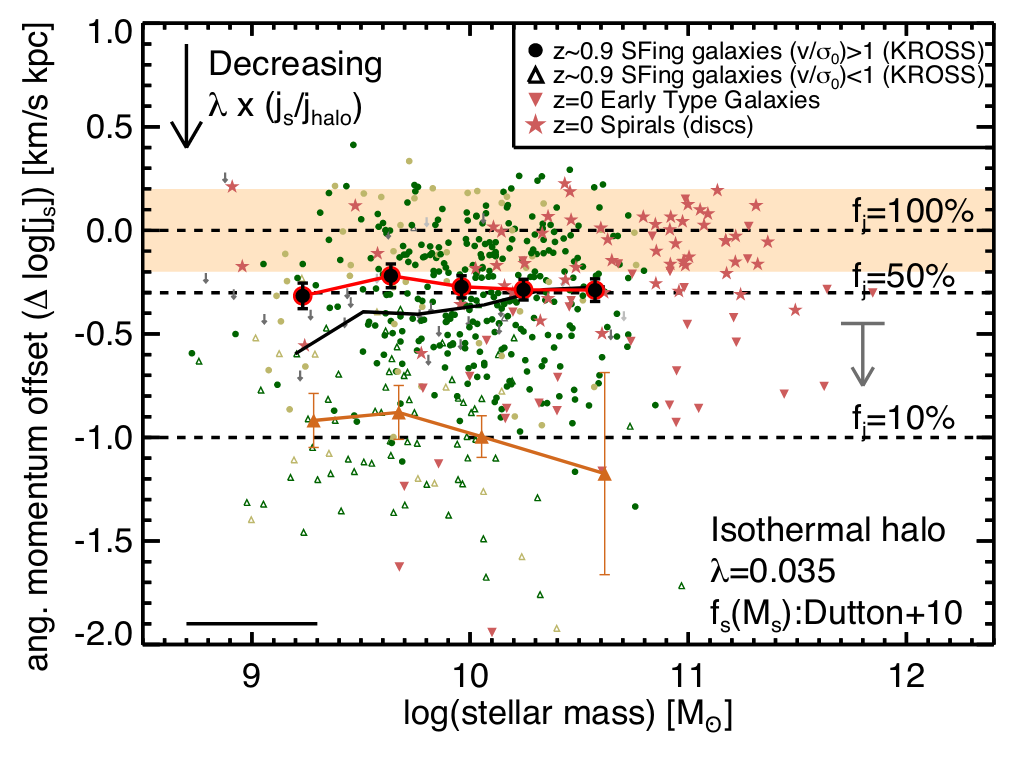
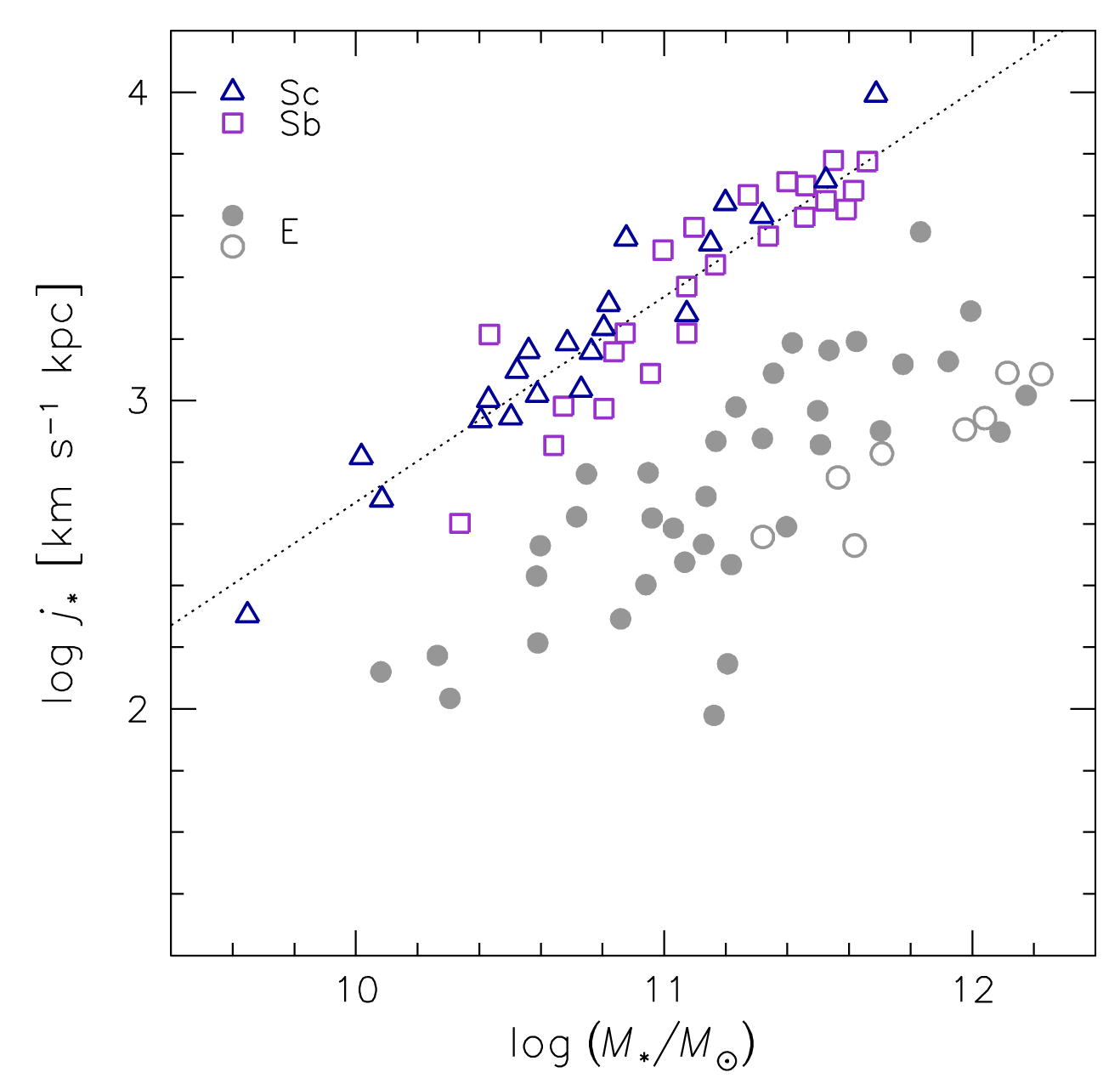
Harrison+17 (KMOS, \(z=1\))






Spiral galaxies \(\leftrightarrow\) high \(J_\star\)
What's the arrow of causality?
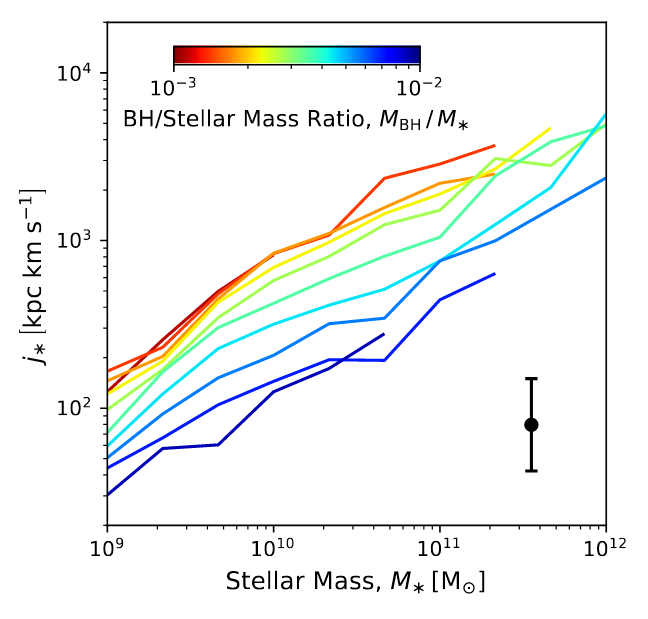
Rodriguez-Gomez+22 (TNG)


Angular momentum: controls disk formation?
Tillson+15
Dekel&Birnboim 06
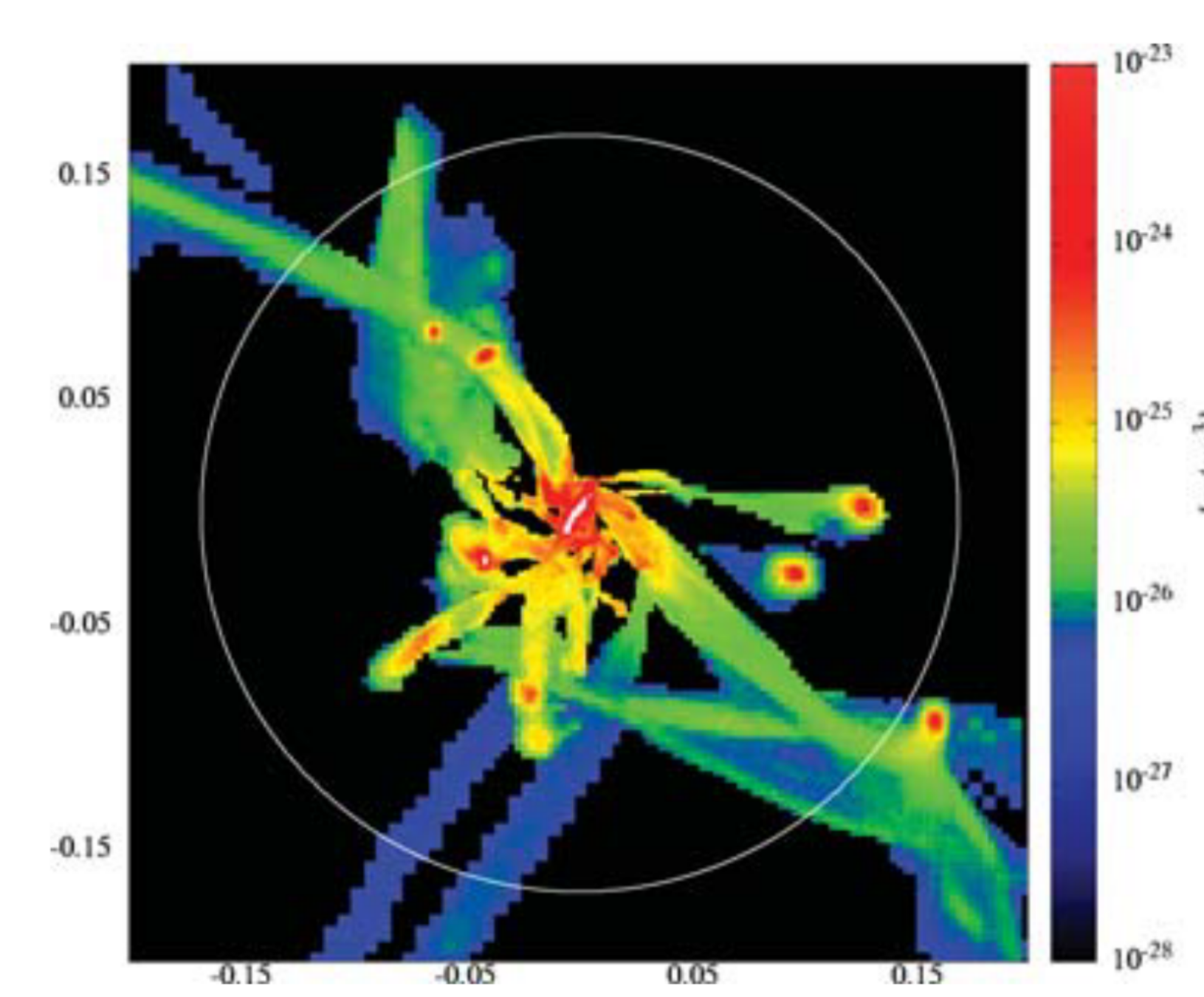
High-z:
most of mass + AM flow along filaments
How do we study these effects?
Large volumes
sample \(p(M_\star, M_\mathrm{DM},\mathbf{J}, d_\mathrm{fil}, \dots)\)
This talk
sample \(p(\mathbf{J}|M_\star, M_\mathrm{DM}, d_\mathrm{fil}, \dots)\)
Angular momentum: bridging galaxy to cosmology
Lower-zs:
intrinsic alignment problem

Angular momentum: where are we?

Porciani+02
Rodriguez-Gomez+22
Predictions for \(j_\mathrm{DM}\) remain qualitative
\(j_\mathrm{DM}-j_\mathrm{\star}\)
weak correlation
(statistically strong)
- Is \(j_\mathrm{DM}\) chaotic or our theory poor?
- Do \(j_\mathrm{gal}\) retain memory of their environment?
-
How is AM transported to the disk?



1. Is \(j_\mathrm{DM}\) chaotic or our theory poor?
First controlled experiment of testing tidal torque theory for individual halos
CC+21a, arXiv: 2012.02201
2. Do \(j_\mathrm{gal}\) retain memory
of the environment?
3. How is AM transported
to the disk?
1. Is \(j_\mathrm{DM}\) chaotic or our theory poor?
2. Do \(j_\mathrm{gal}\) retain memory
of the environment?
First controlled experiment of angular momentum accretion on individual galaxies
CC+22, arXiv: 2206.11913
Main idea: stars are deeper in potential well so less sensitive to what happens at large scales
⇒ stellar Lagrangian patch should be more stable to perturbations
3. How is AM transported
to the disk?
1. Is \(j_\mathrm{DM}\) chaotic or our theory poor?
2. Do \(j_\mathrm{gal}\) retain memory
of the environment?
3. How is AM transported
to the disk?
CC+Pichon+Dubois, 21, arXiv: 2110.05384
Kocjan, CC in prep.

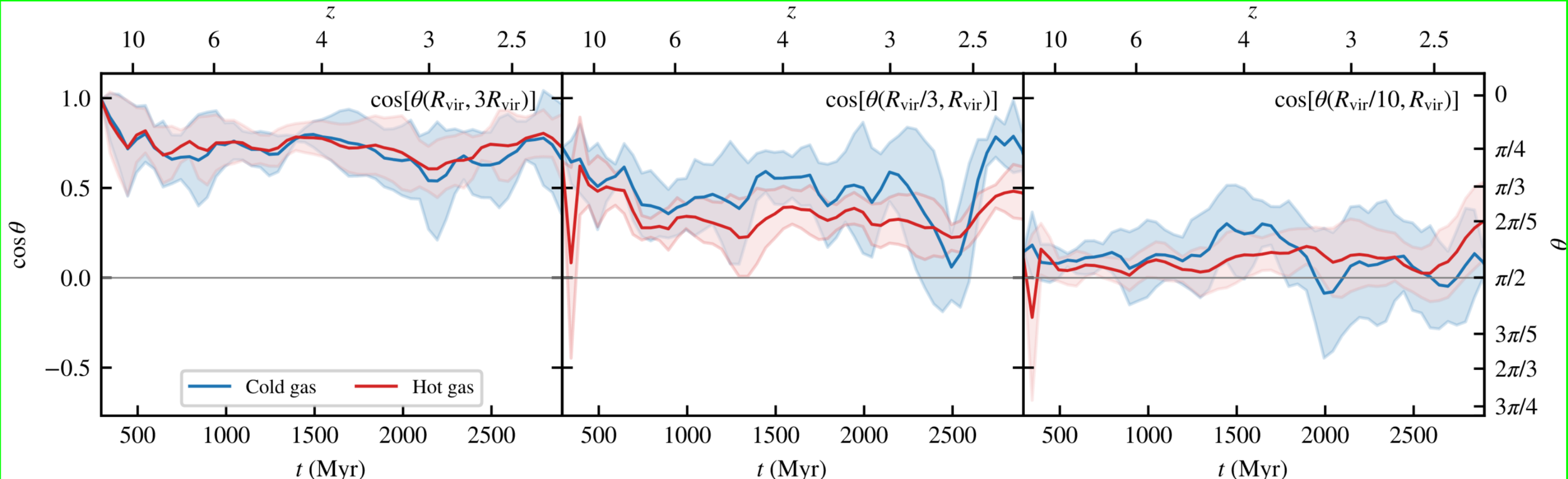
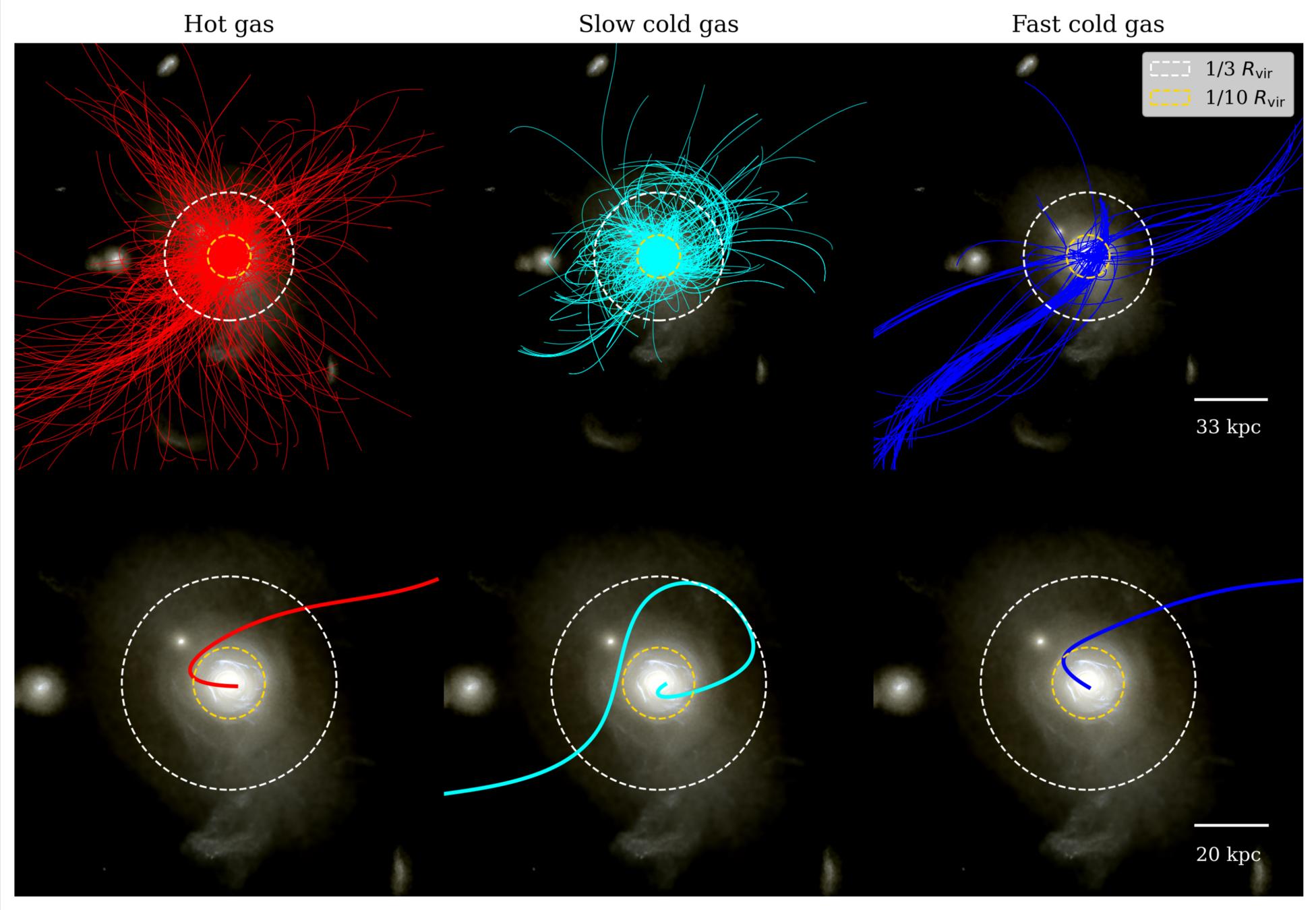
Dynamics of angular momentum
Realignment between…
…\(3R_\mathrm{vir}\) and \(R_\mathrm{vir}\)
…\(R_\mathrm{vir}\) and \(R_\mathrm{vir}/3\)
…\(R_\mathrm{vir}\) and \(R_\mathrm{vir}/10\)
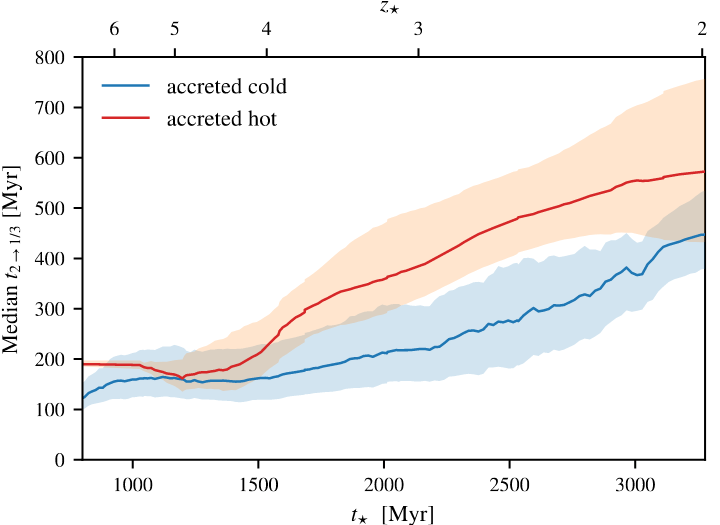
✅ Most of realignment happens in “CGM” (\(\leq R_\mathrm{vir}/3\))
Mostly due to grav. torques (consistent with e.g. Danovich+15)
[CC+21]
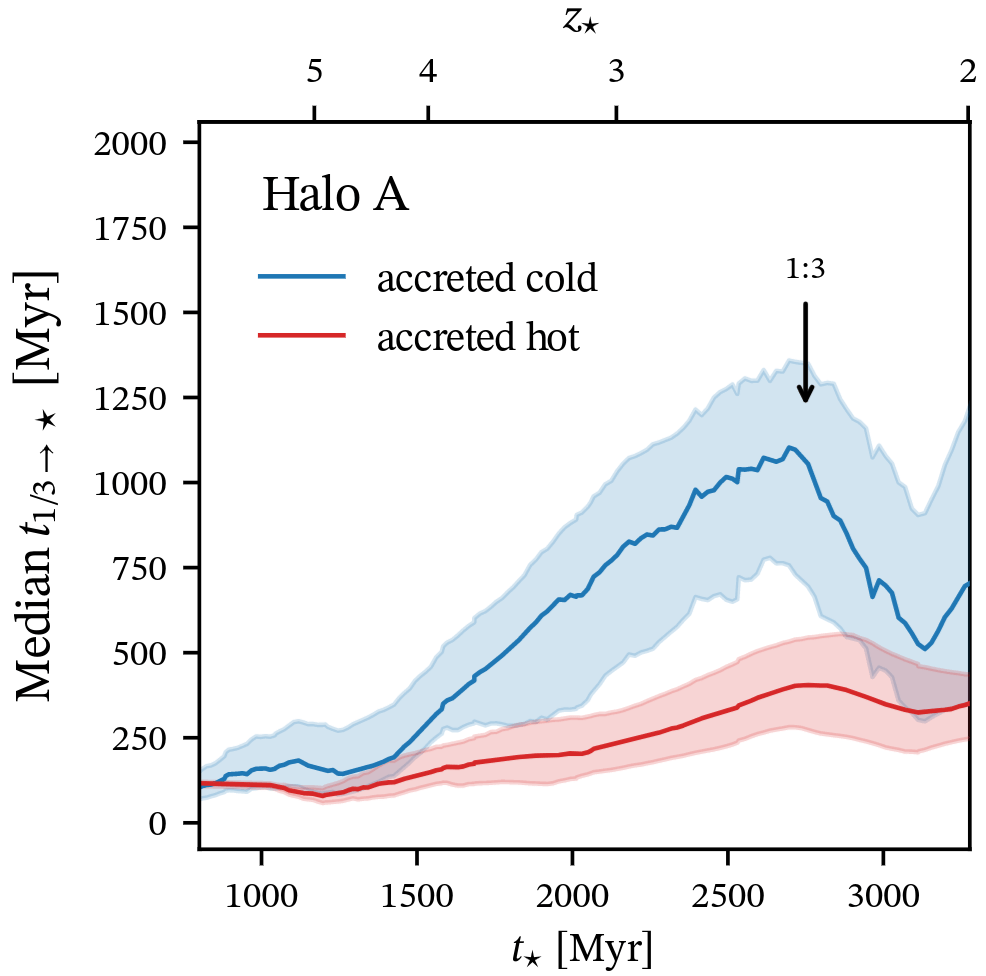
\(t_{1/3}\)
\(t_{\star}\)
\(T_\mathrm{max}\) between \(2 R_\mathrm{vir}\) and \(R_\mathrm{vir}/3\)?
\(\leq 3\times10^4\,\mathrm{K}\)
Cold accretion
\(\geq 5\times10^5\,\mathrm{K}\)
Hot accretion
[Kocjan, CC+ in prep]
What happens in the CGM?



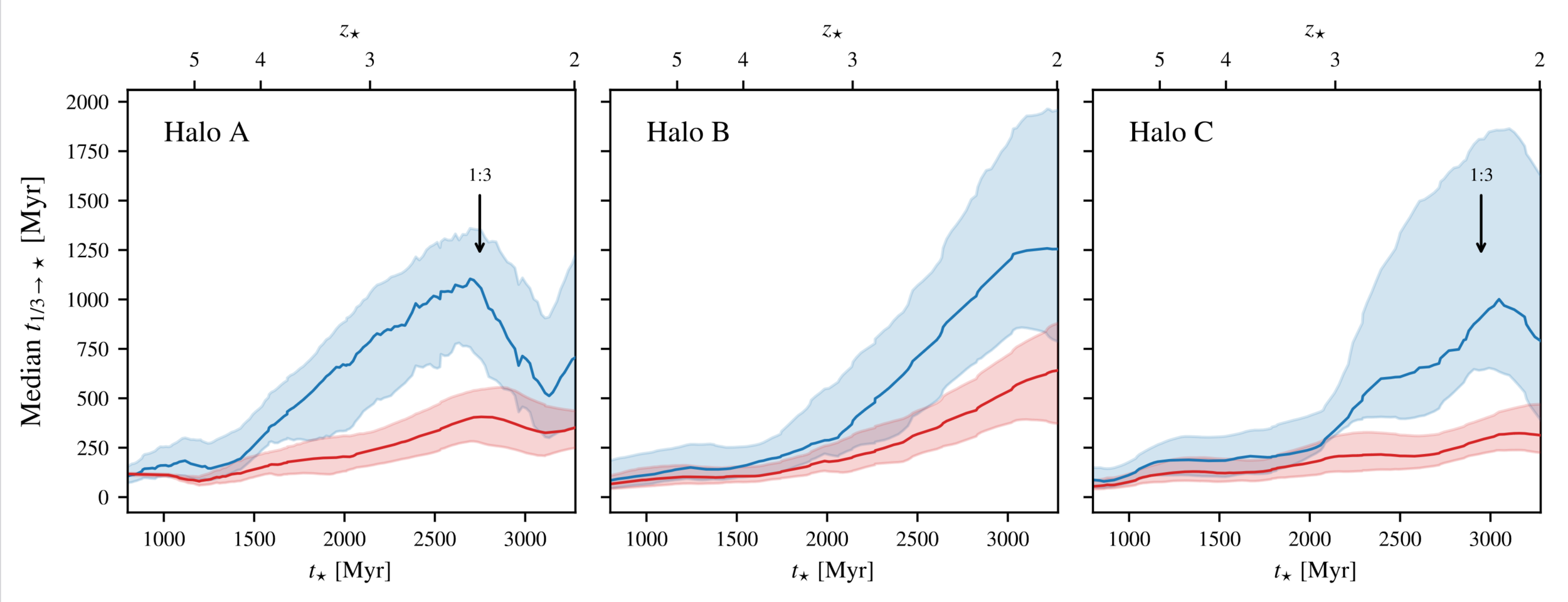

✅ Cold accretion is slow to form stars
Quick depletion right after merger
[Kocjan, CC+ in prep]
The effects of environment on halo properties
Kraljic+18 [see also Laigle15, Song+21,…]
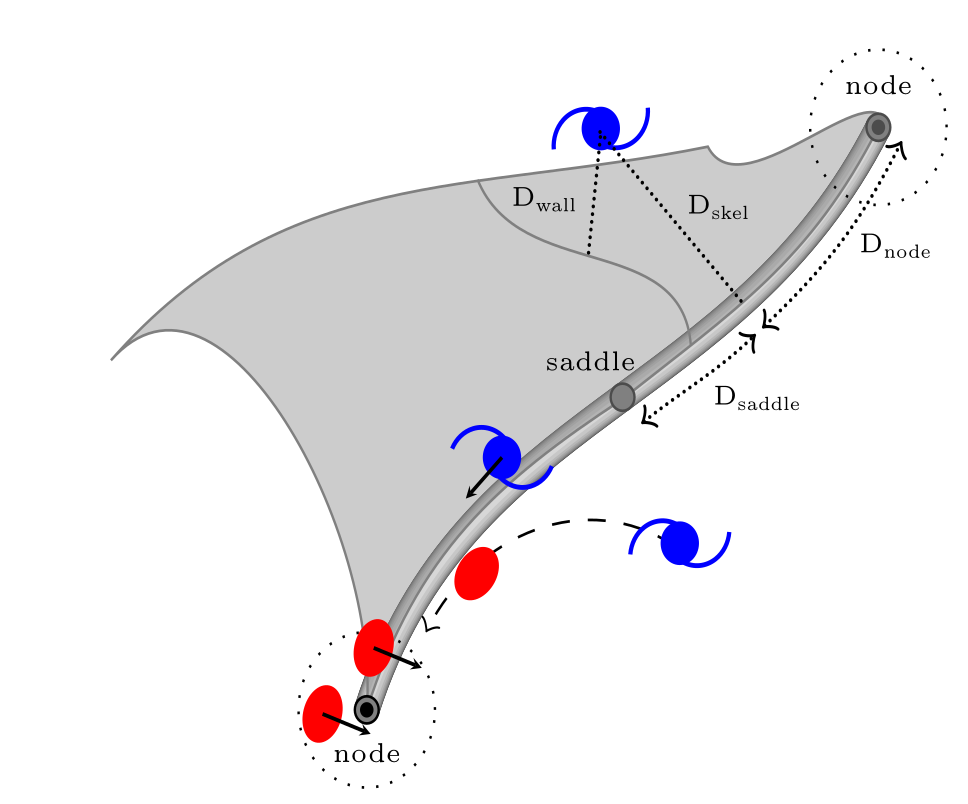



- \( M_\mathrm{DM}(\text{node}) \) > \(M_\mathrm{DM}(\text{fil}) \) >\(M_\mathrm{DM}(\text{void})\), higher clustering
- spins align with cosmic web ⇒ issue for weak lensing
- \(v/\sigma(\mathrm{fil})>v/\sigma(\mathrm{void})\) ⇒ bias in galaxy formation
- ….
The effects of environment on halo properties




Isotropic effects
Kaiser bias, cluster vs. groups, ...
From theory: \(M\propto \int\mathrm{d}^3R\rho\)
Mass regulated
An-isotropic effects
Intrinsic alignment, formation of disks?
From theory: \(J \propto \int\mathrm{d}^3R \nabla \phi\)
Angular momentum regulated?
Predicting angular momentum



\(z=0\)
\( z = 100\)
\[\mathbf{L}_\mathrm{lin.} \propto \int\mathrm{d}^3q(\mathbf{q}-\bar{\mathbf{q}})\times \nabla\phi\]
Position w.r.t. center
Velocity
[White 84]

Note: vanishes at 1st order in a sphere
\[ \int_\Gamma \mathrm{d}^3{q}(\mathbf{q}-\mathbf{\bar{q}}) \times\nabla\phi = \int_{\partial\Gamma}\phi(q)(\mathbf{q}-\mathbf{\bar{q}})\times\mathrm{d}\mathbf{S}\]
Note: the following is a (poor) approximation:
\[ \mathbf{L} \propto \epsilon_{ijk} T_{jl}I_{lk},\quad\text{with \textbf{T} the tidal tensor and \textbf{I} the inertia tensor}\]

Ongoing work by Z. Kocjan

[Kocjan, CC+ in prep]
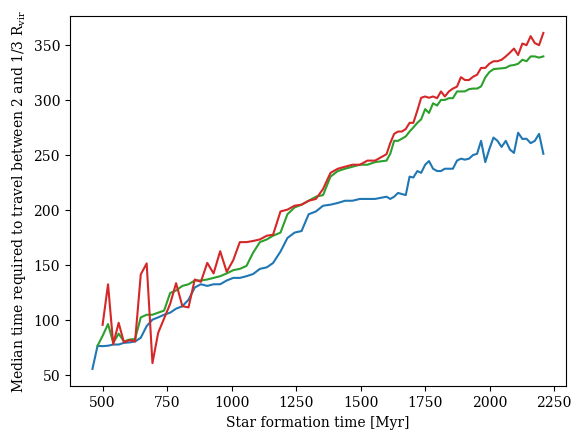
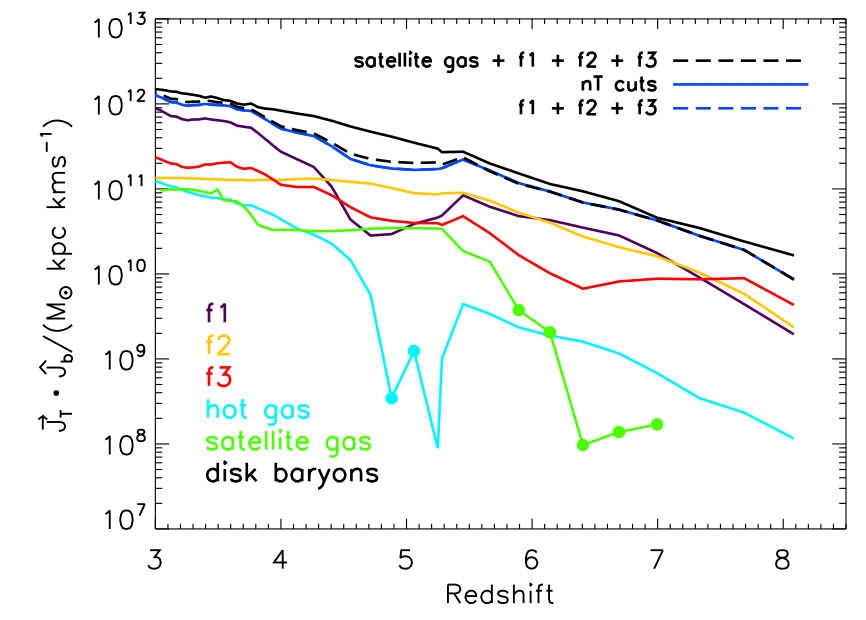
Filamentary accretion ~ Cold flow = \(T \leq 10^5\mathrm{K}\) for \(0.3R_\mathrm{vir} < r < 2R_\mathrm{vir}\)


Filamentary accretion ~ Cold flow = \(T \leq 10^5\mathrm{K}\) for \(0.3R_\mathrm{vir} < r < 2R_\mathrm{vir}\)
Not necessarily fast-track to star formation ⇒ lose connection to CW?
[Kocjan, CC+ in prep]
\(M_\mathrm{DM}(z=2)\approx 10^{11}-10^{12} \mathrm{M_\odot}\)
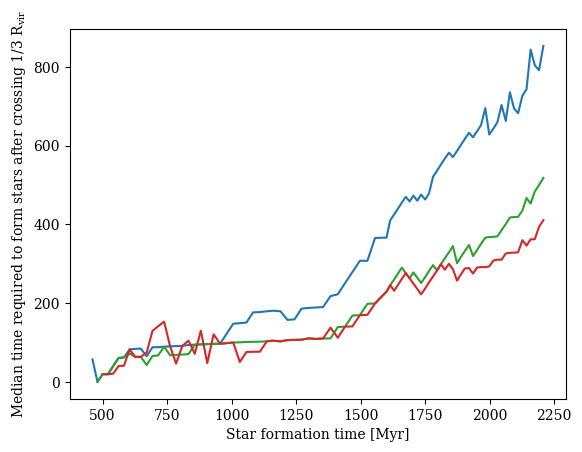

Ongoing work by Z. Kocjan
Ex Uno Plures: direct measure of the impact of the cosmic web on individual objects to shed light on their population statistics



Corentin Cadiou
The Co-evolution of the CW and Galaxies across Cosmic Time

The causal origin of DM halo concentration


$$\rho_\mathrm{DM}(r) = \frac{\rho_0}{\frac{r}{R_\mathrm{vir}/c} \left(1 + \frac{r}{R_\mathrm{vir}/c}\right)^2}$$
Wechsler+02
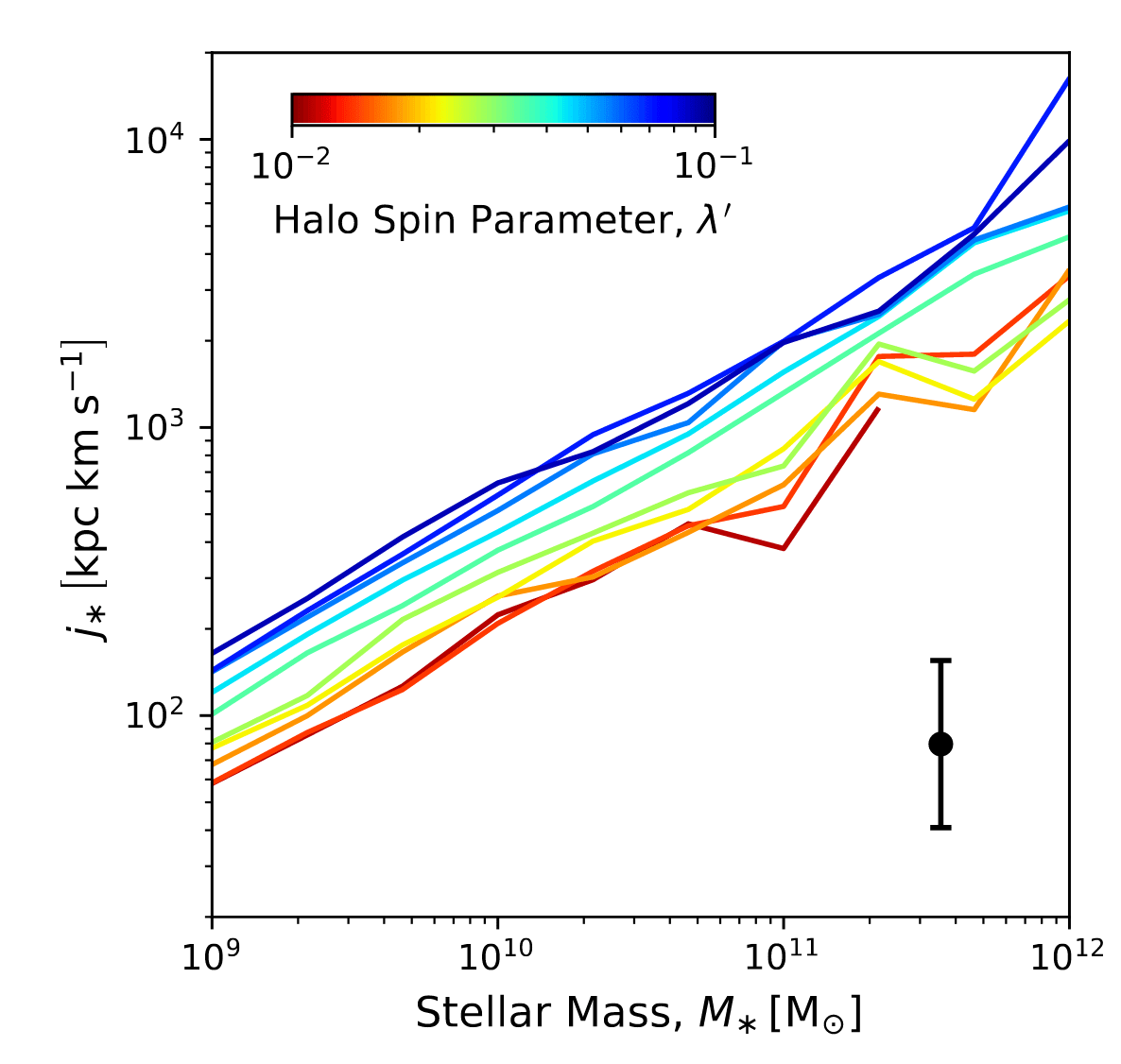
Origin of scatter at fixed \(M_\mathrm{vir}\)?
Predicting angular momentum



- Angular momentum of individual regions can be predicted accurately.
- AM of halos ⇒ requires boundaries of patch


\[\mathbf{L}_\mathrm{lin.} \propto \int\mathrm{d}^3q(\mathbf{q}-\bar{\mathbf{q}})\times \nabla\phi\]
[On patch boundaries: see Lucie-Smith+18]
Can we control baryonic
angular momentum?
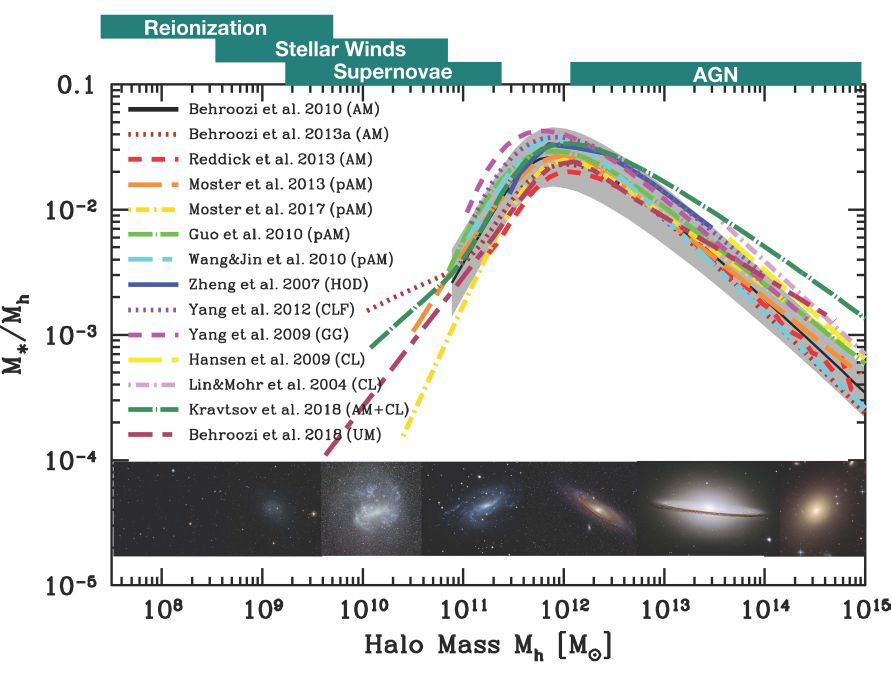
Wechsler & Tinker 18
\({\color{red}M_\star} / M_\mathrm{h} \ll \Omega_b / \Omega_m \)
⇒ baryons & DM stem from different regions


Baryons more strongly bound
⇒ less prone to being ejected



Verify that
\[\xi_\mathrm{lin}(r) \sim \left\langle {\color{green}\underbrace{\delta(x=d)}_\mathrm{in}} {\color{purple} \underbrace{\delta(x=d+r)}_\mathrm{out}}\right\rangle \]
is the same in spliced / ref simulation.

Verify that
\[\xi_\mathrm{lin}(r) \sim \left\langle {\color{green}\underbrace{\delta(x=d)}_\mathrm{in}} {\color{purple} \underbrace{\delta(x=d+r)}_\mathrm{out}}\right\rangle \]
is the same in spliced / ref simulation.

Verify that
\[\xi_\mathrm{lin}(r) \sim \left\langle {\color{green}\underbrace{\delta(x=d)}_\mathrm{in}} {\color{purple} \underbrace{\delta(x=d+r)}_\mathrm{out}}\right\rangle \]
is the same in spliced / ref simulation.

Temporary conclusions
-
angular momentum is predictable
-
boundary of halos in the ICs is a hard problem
⇒ limits practicality of predictions (for now)
-
baryons appear to be simpler!
⇒ good news for weak lensing predictions
⇒ key to understand morphology


Galaxy formation in cosmology: the role of the environment




Environmental effects:
- source of “pollution” in weak lensing surveys
⇒ intrinsic alignment
- extra parameters in semi-analytical models
⇒ galaxy-halo correlation




+

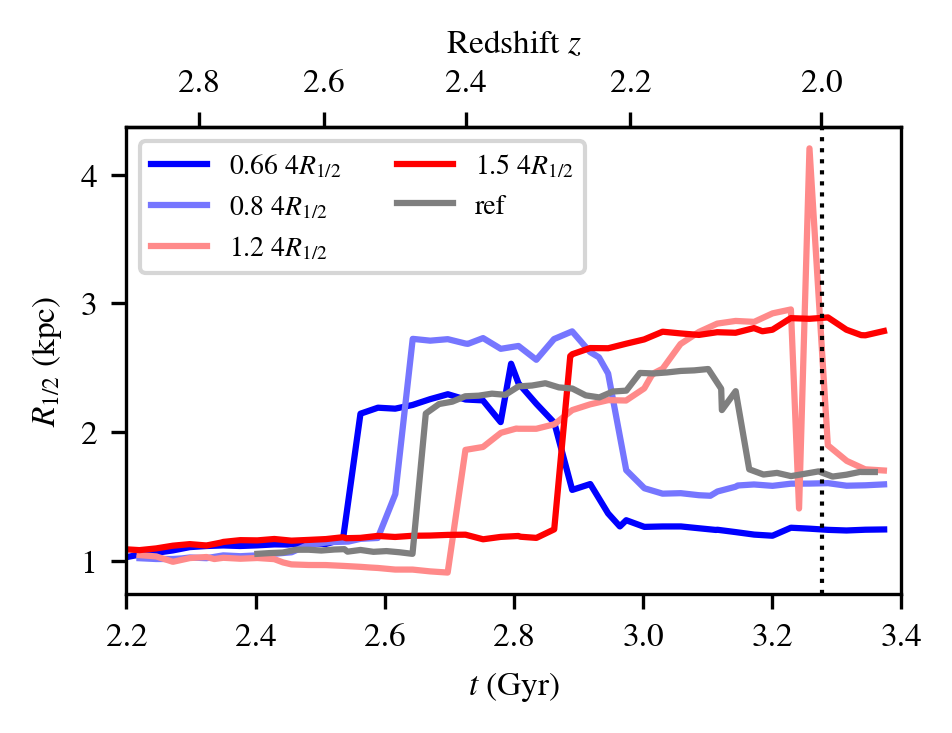
\( R_{1/2} \)
\( l_0 \times 1.2\)
\( l_0 \times 1.5\)

\( l_0 \times 0.66\)
\( l_0 \times 0.8\)

\( l_0 \times 0.66\)
\( l_0 \times 0.8\)
\( l_0 \times 1.2\)
\( l_0 \times 1.5\)


\( l_0 \times 1.2\)
\( l_0 \times 1.5\)

\( l_0 \times 0.66\)
\( l_0 \times 0.8\)



\( l_0 \times 1.2\)
\( l_0 \times 1.5\)

\( l_0 \times 0.66\)
\( l_0 \times 0.8\)



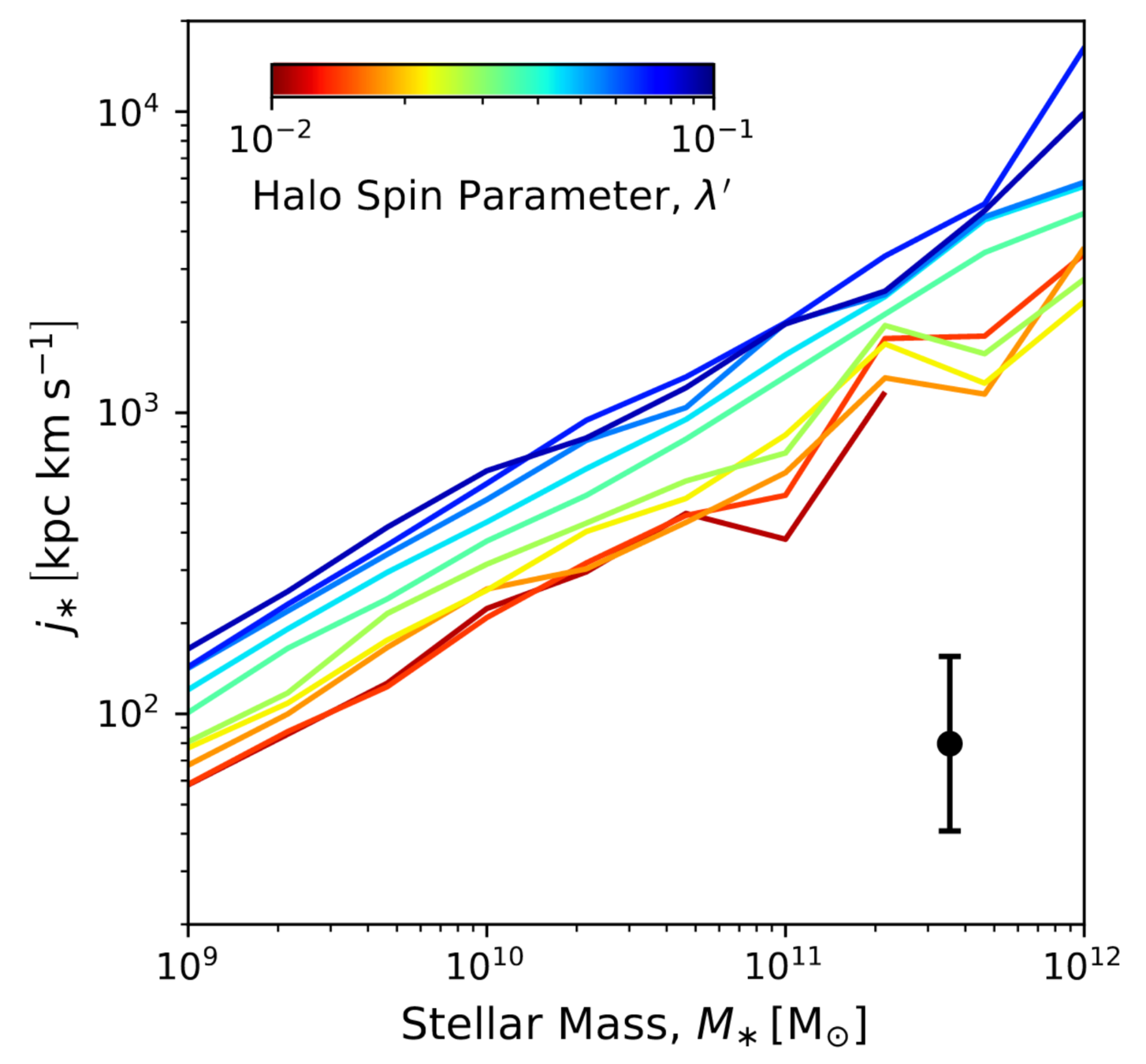
- AM of baryons originates from initial conditions…
- can be controlled…
- and regulate galaxy morphology
- Negligible AGN/SN global self-regulation
Galaxy formation
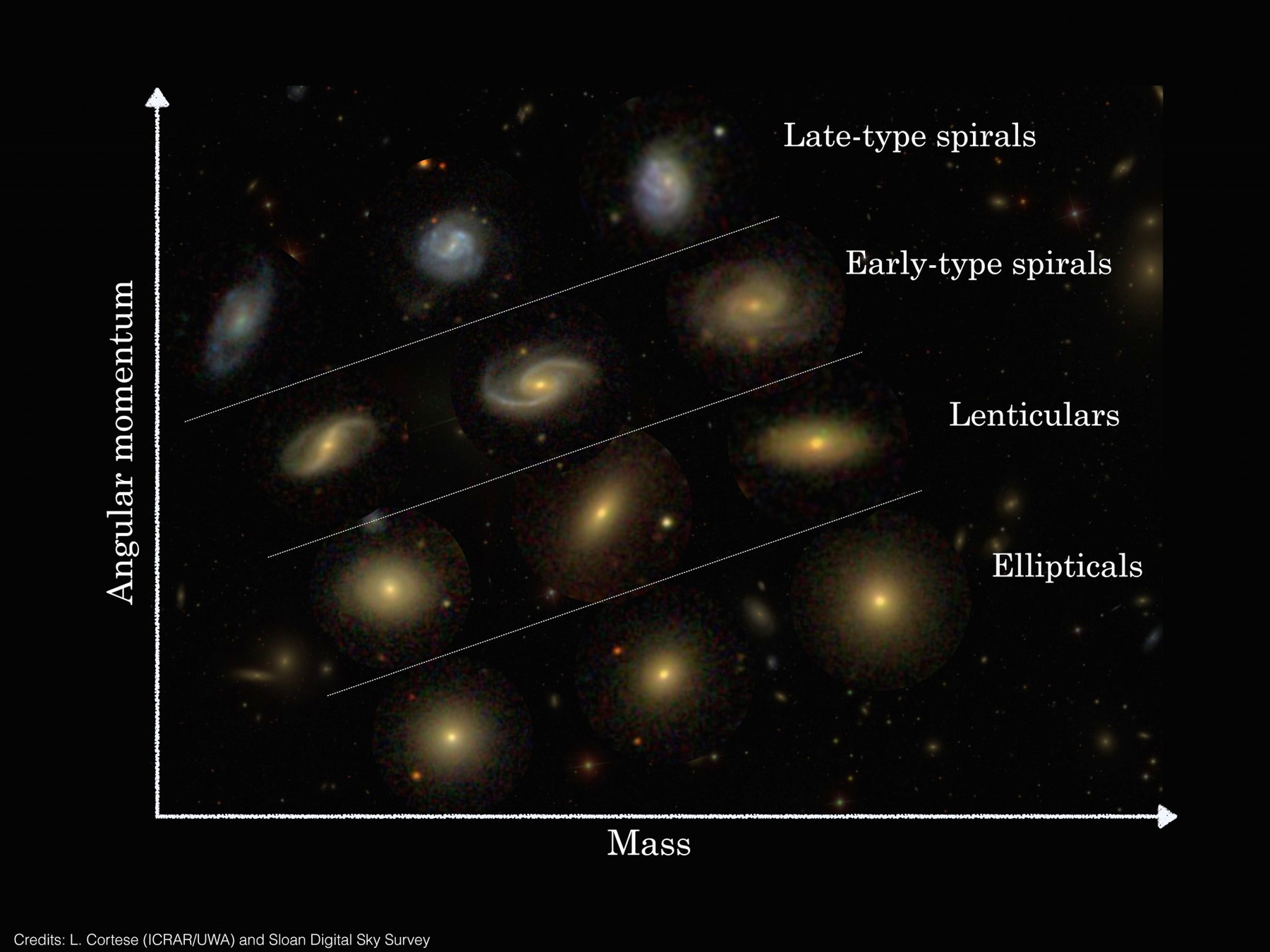
[L. Cortese; SDSS.]



[Dubois+16]
AGN no AGN
Origin of morphological diversity at fixed mass?

[L. Cortese; SDSS.]



[Dubois+16]
AGN no AGN
Origin of morphological diversity at fixed mass?
How to explain environmental effects?

[Kraljic+ in prep]

Galaxy formation

[Danovich+15]
The origin of high \(z\) angular momentum

[Danovich+15]
I. Torque with cosmic web
The origin of high \(z\) angular momentum

[Danovich+15]
I. Torque with cosmic web
II. Transport at constant AM
The origin of high \(z\) angular momentum

[Danovich+15]
I. Torque with cosmic web
II. Transport at constant AM
III. Torque down in inner halo
The origin of high \(z\) angular momentum

[Danovich+15]
I. Torque with cosmic web
II. Transport at constant AM
III. Torque down in inner halo
IV. Mixing in inner disk & bulge
The origin of high \(z\) angular momentum
The origin of high \(z\) angular momentum

[Danovich+15]
IV. Mixing in inner disk & bulge
Fraction that ends up in disk vs. IGM?
Influence of galactic physics?
III. Torque down in inner halo
Origin of torque down (pressure or gravity)?
Loss of link with cosmic AM?
II. Transport at constant AM
Same evolution in cold/hot accretion modes?
I. Torque with cosmic web
Predict pre-accretion AM?
Alignment with environment?
The origin of high \(z\) angular momentum

[Danovich+15]
IV. Mixing in inner disk & bulge
Fraction that ends up in disk vs. IGM?
Influence of galactic physics?
III. Torque down in inner halo
Origin of torque down (pressure or gravity)?
Loss of link with cosmic AM?
See Cadiou+21c
II. Transport at constant AM
Same evolution in cold/hot accretion modes?
I. Torque with cosmic web
Predict pre-accretion AM?
Alignment with environment?
The origin of high \(z\) angular momentum

[Danovich+15]
IV. Mixing in inner disk & bulge
Fraction that ends up in disk vs. IGM?
Influence of galactic physics?
III. Torque down in inner halo
Origin of torque down (pressure or gravity)?
Loss of link with cosmic AM?
II. Transport at constant AM
Same evolution in cold/hot accretion modes?
I. Torque with cosmic web
Predict pre-accretion AM?
Alignment with environment?