Corentin Cadiou
PDRA @ Lund Sweden
Chargé de recherche @ IAP from February
Star formation
Star formation rate is given by
\[\frac{\Delta M_\star}{\Delta t} = \epsilon_\mathrm{ff} \frac{m_\mathrm{g}} {t_\mathrm{ff}} \propto m_\mathrm{g}^{3/2},\]
where
- \(t_\mathrm{ff}={0.5427}/{\sqrt{\rho_\mathrm{g}G}}\) and,
- \(\epsilon_\mathrm{ff}\sim 0.01-0.30\) is a user-defined parameter,
- \(\Delta M_{\star,\mathrm{max}}<0.9\times m_\mathrm{g}\) to prevent full depletion of the cell in one step.
SF is only allowed in cells with
\[n_\mathrm{H}>n_\mathrm{th} \quad\text{and}\quad T<T_\mathrm{th},\]
where \(n_\mathrm{th}\) and \(T_\mathrm{th}\) are user-defined density and temperature thresholds (typically \(\sim 10\,\mathrm{cm^{-3}}\) and \(\sim 500-1000\,\mathrm{K}\)).
Stellar particle has mass
\[M_\star=N\times m_\star,\quad \text{with}\quad m_\star = n_\mathrm{th}\Delta x_\mathrm{min}^3 \text{ and } N \sim \mathcal{P}\left(\frac{m_\star}{\Delta M_\star}\right).\]
Note: this is mini-ramses' implementation
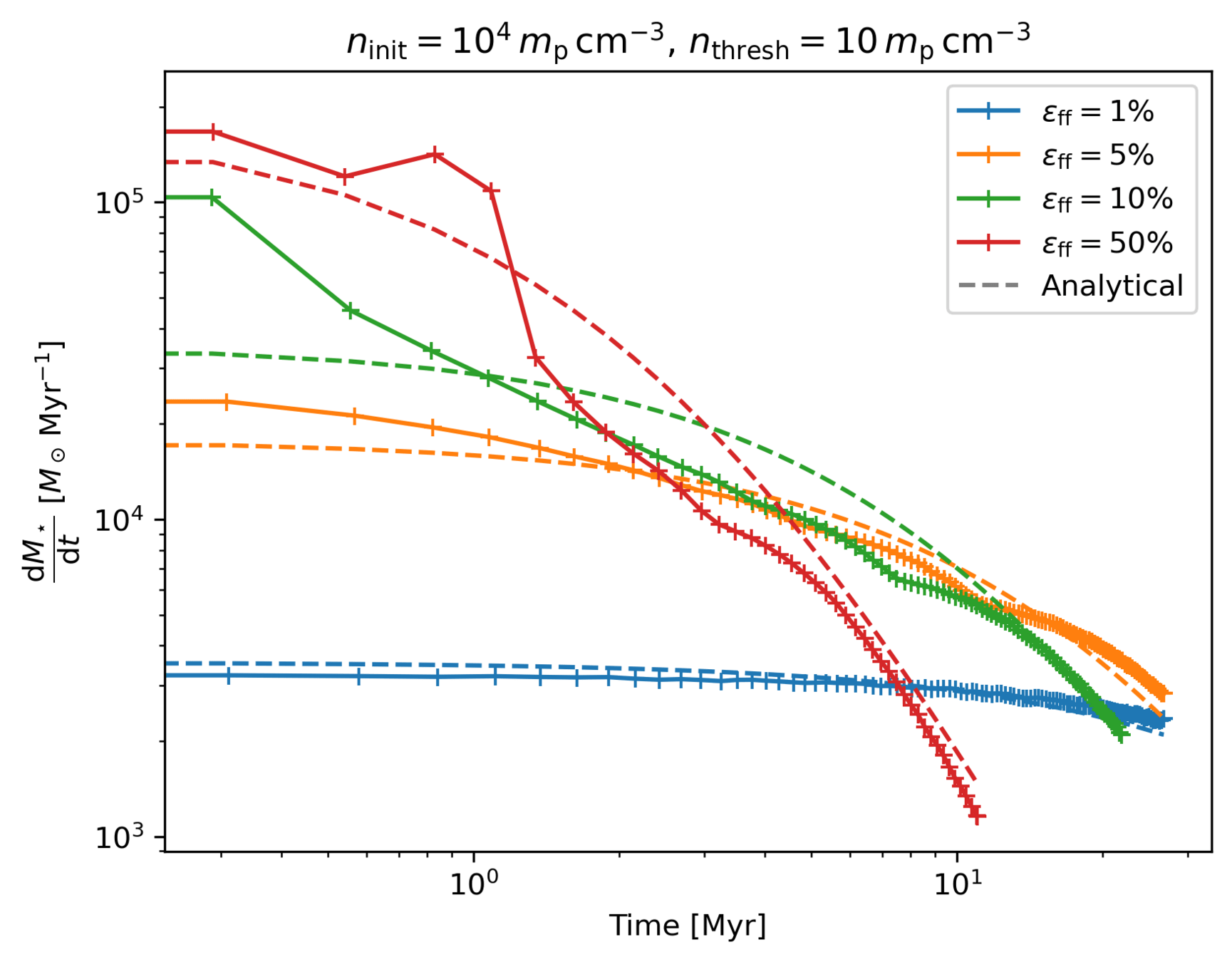
Star formation - test
ICs
- uniform density grid with
\(\rho = 10^4\,m_\mathrm{p}\,\mathrm{cm^{-3}}\), \(L_\mathrm{box} = 10\,\mathrm{pc}\) - SF above \(n_\mathrm{th}= 10\,\mathrm{cm^{-3}}\)
- no gravity
Theoretical DERIVATION
Mass conservation:
\[\dot m_\mathrm{g}+Km_\mathrm{g}^{3/2}=0,\]
where \(K = \sqrt{\frac{\epsilon_\mathrm{ff}^2 G}{0.5427 V}}\), \(V=(10\,\mathrm{pc})^3\) and \(G\) the gravitational constant.
The solution to this equation is
\[m_\mathrm{g} = \frac{4}{(K t - b)^2},\]
with \(b = \sqrt{4 / m_\mathrm{g,i}}\). Given mass conservation, we get the total stellar mass
Analytical solution
\[M_\star(t) = m_\mathrm{g,i}-\frac{4}{(K t - b)^2}.\]
// First pass, count number of cells elligible for SF
uint Nformation_sites = 0;
foreach_cell.reduce_cell( "star_formation_count", U.getShape(),
CELL_LAMBDA(const ForeachCell::CellIndex& iCell, uint32_t& count)
{
[...]
}, Nformation_sites);
// Create temporary views to store particle data
Kokkos::View<real_t*> mp("new_particle_mass", Nformation_sites);
Kokkos::View<real_t**> xp("new_particle_pos", Nformation_sites, 3);
Kokkos::View<real_t**> vp("new_particle_vel", Nformation_sites, 3);
// Second pass, effectively create particle properties
uint Npart_created = 0;
foreach_cell.reduce_cell( "star_formation_spawn", U.getShape(),
CELL_LAMBDA(const ForeachCell::CellIndex& iCell, uint32_t& count)
{
[...]
}, Npart_created);
// Increase the number of particles
uint32_t Npart_old = U.getParticleArray("particles").getNumParticles();
U.growParticleArray("particles", Npart_old + Npart_created);
// Copy the temporary views to the particle array
Kokkos::parallel_for("star_formation_create", Npart_created,
KOKKOS_LAMBDA(uint32_t iPart)
{
[...]
});Shortcomings:
- Many formation sites, few stars created
- Two passes required
- Growing array: temporarily doubles memory + is slow
\(\mathcal{O}(N_\mathrm{part})\)
- Analytical
- No metallicity dependence
- Simple redshift dependence (UV-heating + compton)

Cooling
Theuns+98 implementation
\[\frac{\mathrm{d}u}{\mathrm{d}t} = \left(\frac{1-Y}{m_\mathrm{H}}\right)^2\rho({\color{red}\mathcal{H}}-{\color{blue}\mathcal{C}})\]
foreach_cell.foreach_cell("cooling", U.getShape(),
CELL_LAMBDA(const ForeachCell::CellIndex& iCell)
{
while (t_cool < dt * scale_t) {
// Get abundances (in eq or not)
real_t HI = interpolate( HI_table, iz, iT, inH);
[...]
real_t HeIII = interpolate(HeIII_table, iz, iT, inH);
real_t e = HII + HeII + 2 * HeIII;
// Compute heating/cooling terms [erg/s.cm**3]
real_t net_cooling, H, C;
C = cooling(T_over_mu, nH, z, e, HI, HII, HeI, HeII, HeIII);
H = heating(nH, z, HI, HeI, HeII);
// Compute cooling [K/s]
net_cooling = (C - H) * nH / threekB_over_twoX;
// Cooling timescale [s]
dt_cool = FMIN(
// do not allow more than 25% change in temperature
FABS(T_over_mu * 0.25 / net_cooling),
// do not overshoot the remaining time
dt * scale_t - t_cool
);
T_over_mu -= net_cooling * dt_cool;
// Update cooling time
t_cool += dt_cool;
Nstep++;
}
}};Pros/cons:
- Already supports non-eq chemistry [untested],
- Stability issues and negative pressures
- Warp divergence on GPUs
Units
The old RAMSES way
subroutine dummy_sfr
call units([...], scale_d, [...], aexp)
do icell = 1, ncell ! Loop over cells
rho = uold(icell, 1) / scale_d ! Convert to g/cm**3
rho = uold(icell, 1) * scale_d ! Which one is correct?
rho = rho / mp ! Convert to mp/cm**3
if (rho < rho_treshold) then ! Implicit: rhs is in mp/cm**3
! do stuff
end if
end do
end subroutineUnits
two distinct problems
- unitful inputs/outputs
- conversion to/from code units
Discussion points:
- Code units are comoving → conversion is time-dependent
// In kernel:
// real → code units [comoving]
real_t rho = Uin.at(iCell, IRho);
// The RAMSES' way
real_t rho_cgs = rho * some_conversion_factor;
// BETTER?
if (rho < rho_treshold.toCode) {...}
if (rho < 10 * mp_per_cc.toCode) {...}
rho * mp_per_cc.fromCode;Conversion to/from code units
Discussion points:
- either all or no parsing,
- robust parsing is hard.
Input/output units
[star_formation]
rho_threshold = 10 mp/cm**3// Read config file: Dyablo's initialization
auto config = readConfig();
// Get runtime params: plugin initialization
auto rho_threshold = config.get<…>("star_formation", "rho_threshold");typedef Density = Unit<M=1, L=-3>;
typedef Temperature = Unit<Temp=1>;
// In plugins:
// -- init --------------------------------------------------!
Quantity<Density> rho_threshold = configMap.get<Density>("star_formation", "rho_threshold");
auto T_threshold = configMap.get<Temperature>("star_formation", "T_threshold");
// -- update ------------------------------------------------!
auto erg = Units::erg;
auto s = Units::s;
auto cm3 = Units::cm.pow<3>();
Unit<M=1, L=3, T=-3> erg_per_s_cc (erg / s * cm3, scalarData);
real_t rho_threshold = this->rho_threshold.toCode(scalarData);
foreach_cell.reduce_cell("do_stuff", U.getShape(),
CELL_LAMBDA(const ForeachCell::CellIndex& iCell) {
real_t rho = Uin.at(iCell, VarIndex_Cooling::Irho);
if (rho > rho_threshold) {...}
real_t cooling_rate = table(...) * erg_per_s_cc.toCode;
real_t … = cooling_rate * erg_per_s_cc.fromCode;
});// config.ini
[star_formation]
rho_threshold = 10 mp/cm**3Units: Proposed draft
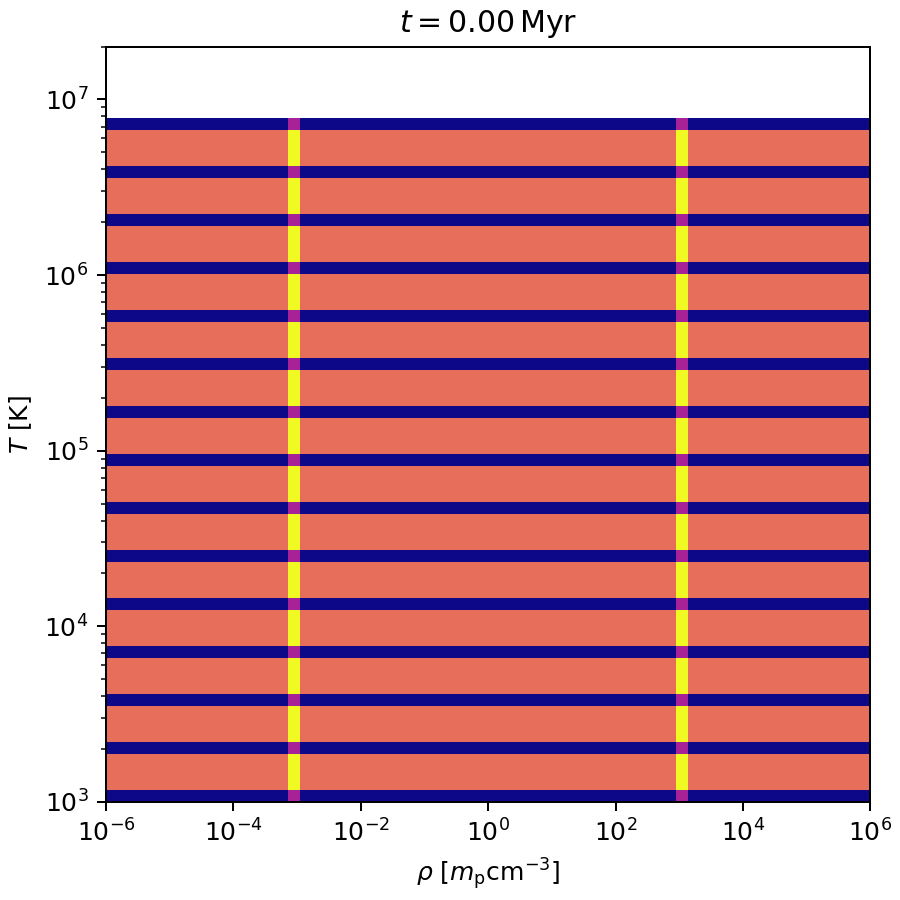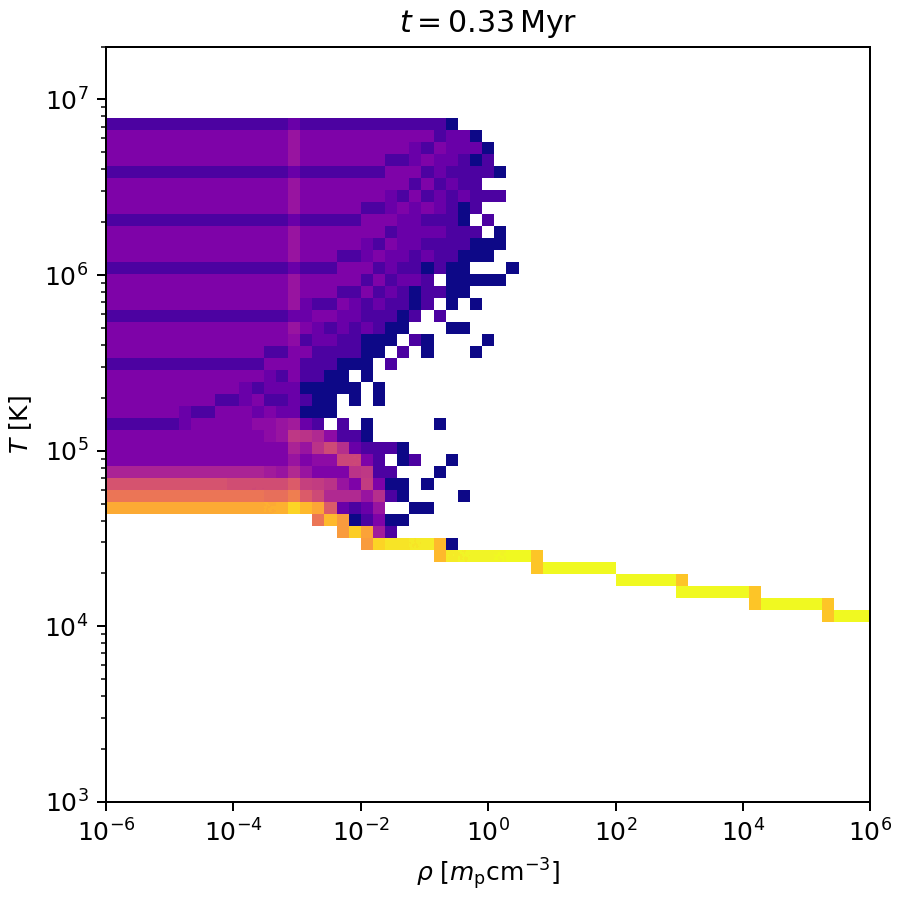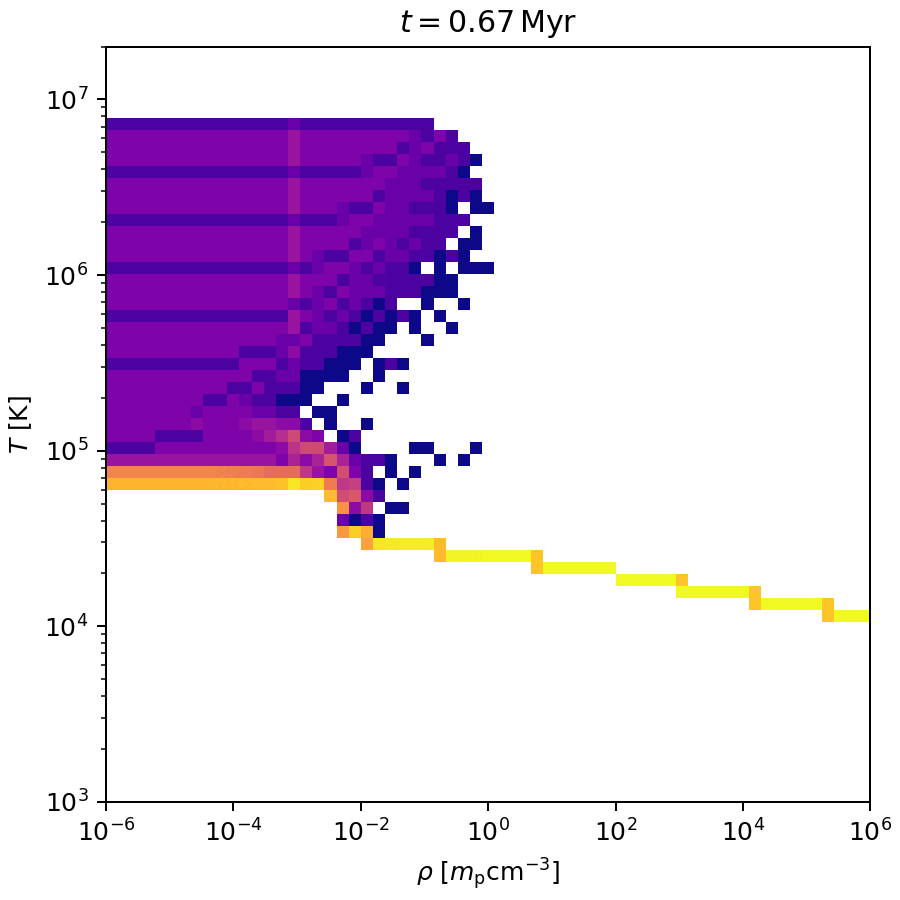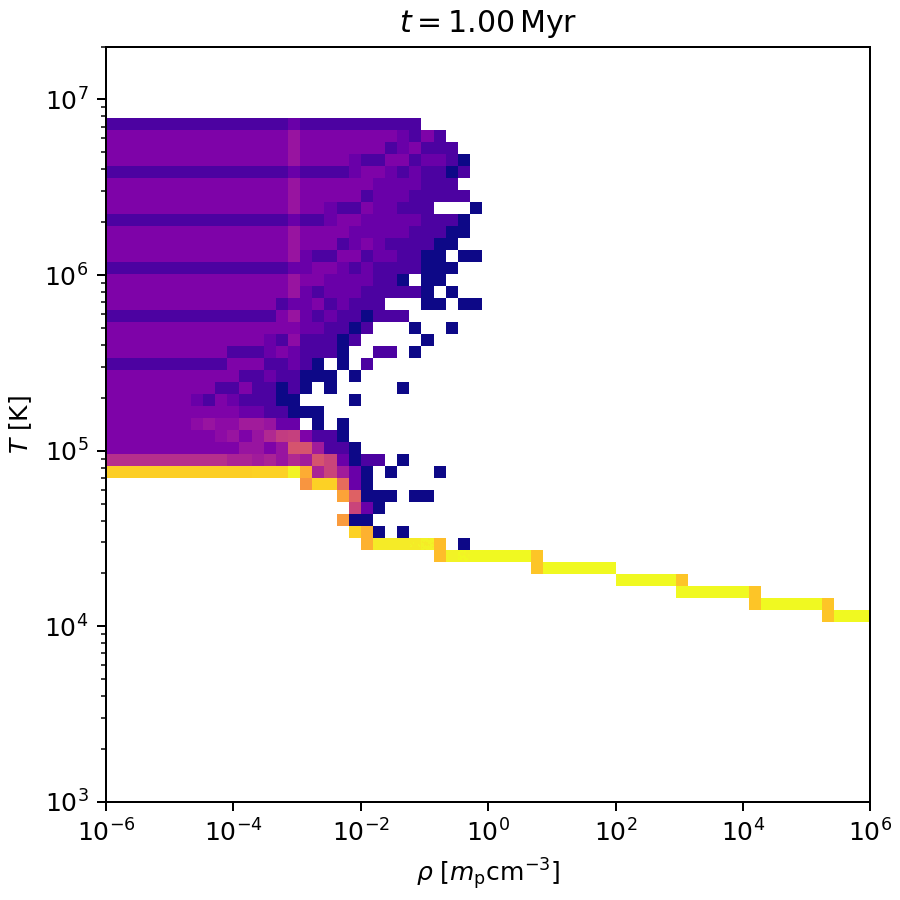
Cooling
Test:
- thin \(x,y\) slab with grid of
\(\rho=10^{-6}-10^6\,m_\mathrm{p}\,\mathrm{cm}^{-3}\)
and
\(T=10^2-10^7\,\mathrm{K}\). - hydro bypassed,
- activate cooling,
- let evolve outputs.
Note 1: \(T\) may be off by factors \(\mu\), \(\Lambda\) may be off by factor \(X\).
Cooling (ctd.)
Now includes
- H. Katz' RTZ model,
- non-equilibrium chemistry,
- includes HI-II, H2, HeI-III, CI-VI, OI-VIII, CO
- coupled to cooling,
-
based on
mdelorme/passive_scalars
TODO:
- couple to RT,
- allow in-equilibrium rather than out-of.
Progress on Dyablo subgrid
Star formation
Feedback
Cooling
IO
+ Monte-Carlo tracer particles (almost working :) )
Corentin Cadiou
Chargé de recherche
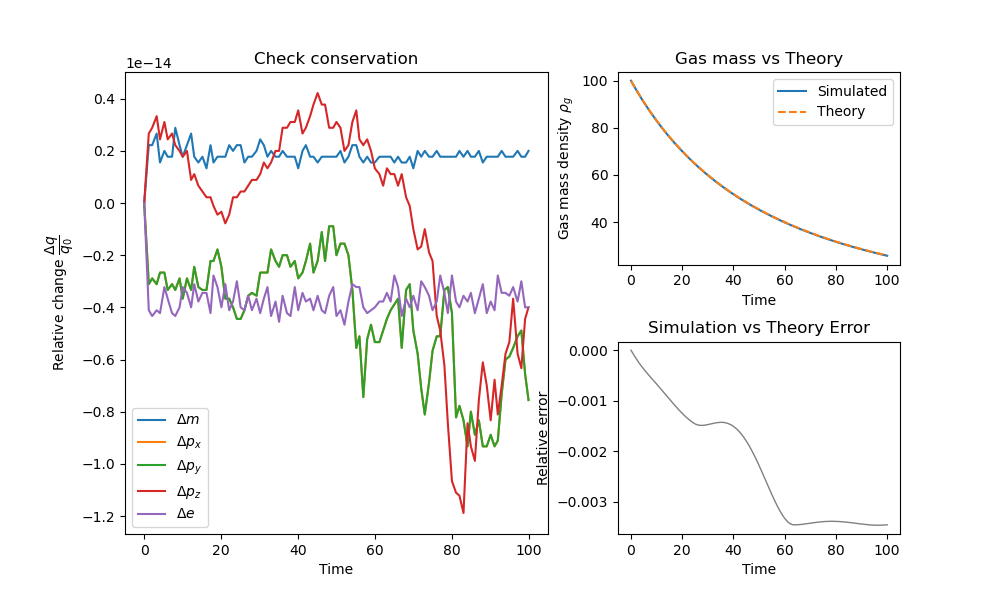
Star formation
Density-based criterion, constant efficiency
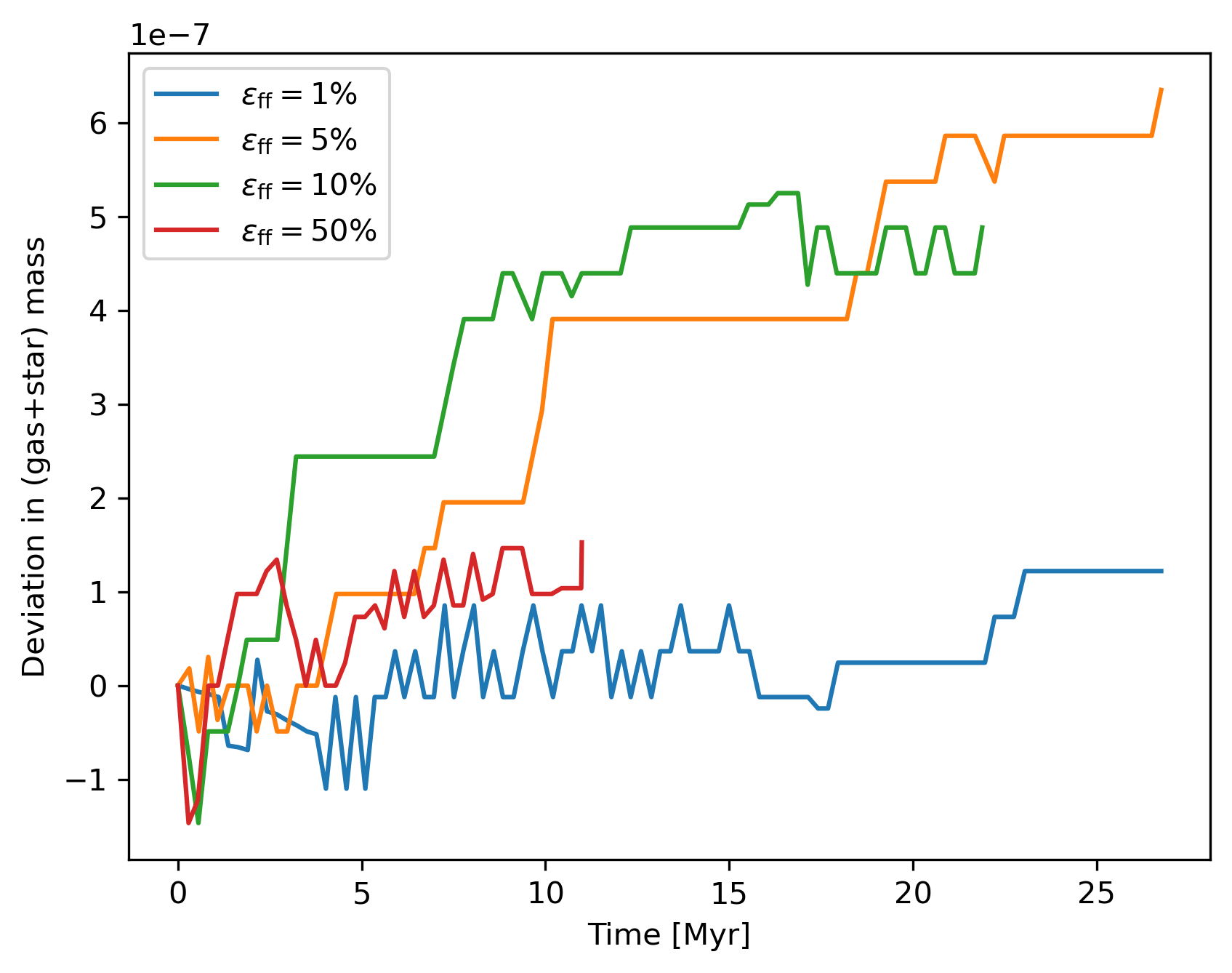
- ✔Mass/momentum/energy conserving
- ✔Fits analytical prediction
Feedback
Thermal injection only
- ✔Mass/momentum/energy conserving
- ✔Fits analytical prediction
Cooling
Using Grackle cooling tables + 3rd order implicit solver
- ✔UV background
- ✔Metal cooling
- ✔Fits analytical prediction
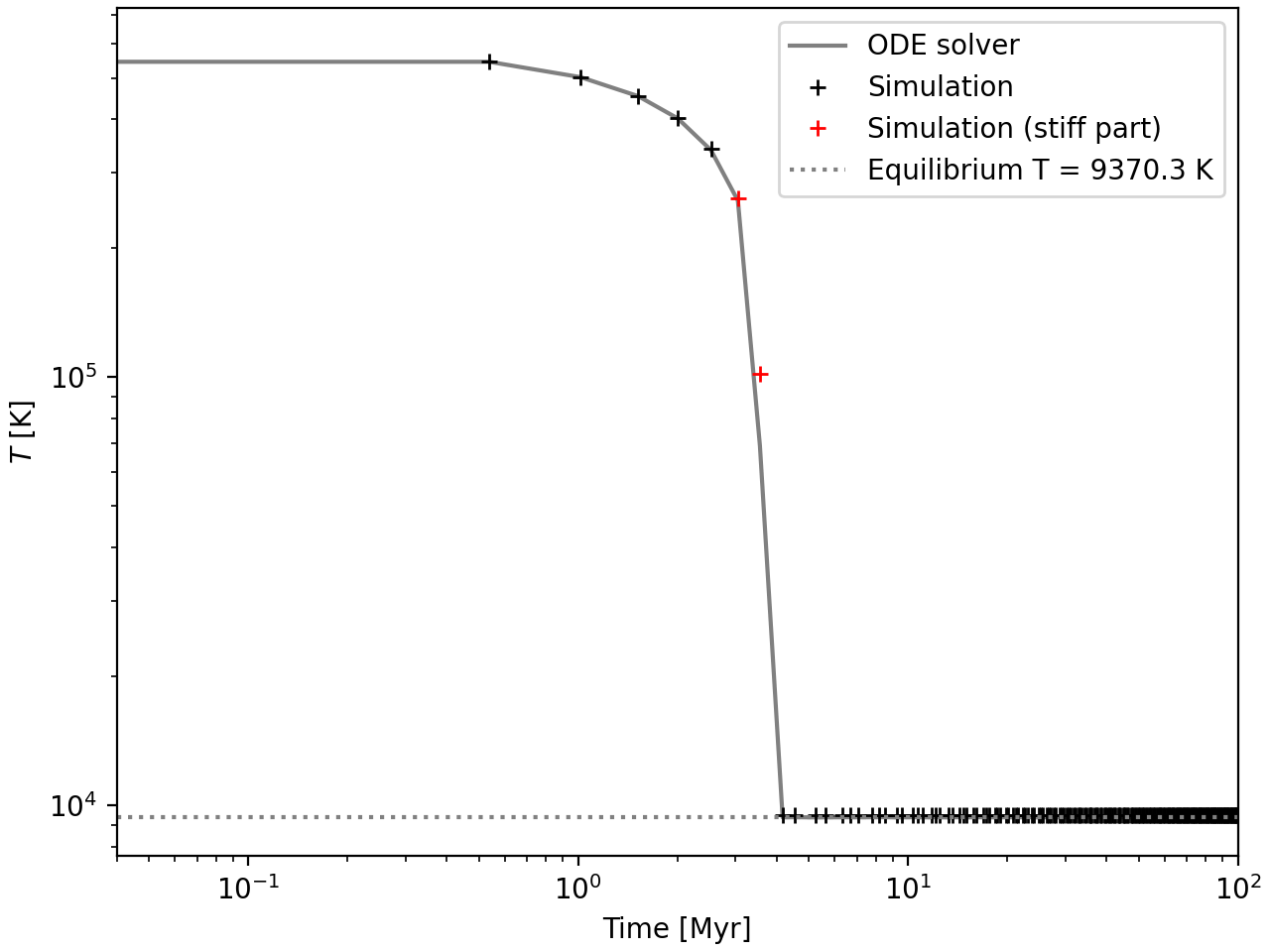
IO
Support for Gadget format (simple HDF5 particle-based files)
- ✔Mass/momentum conserving
- ✔Proper SPH interpolation
- Not MPI parallelized
Ideal for small setups
Input (GADGET simulation)
Output (Dyablo, w/ AMR)
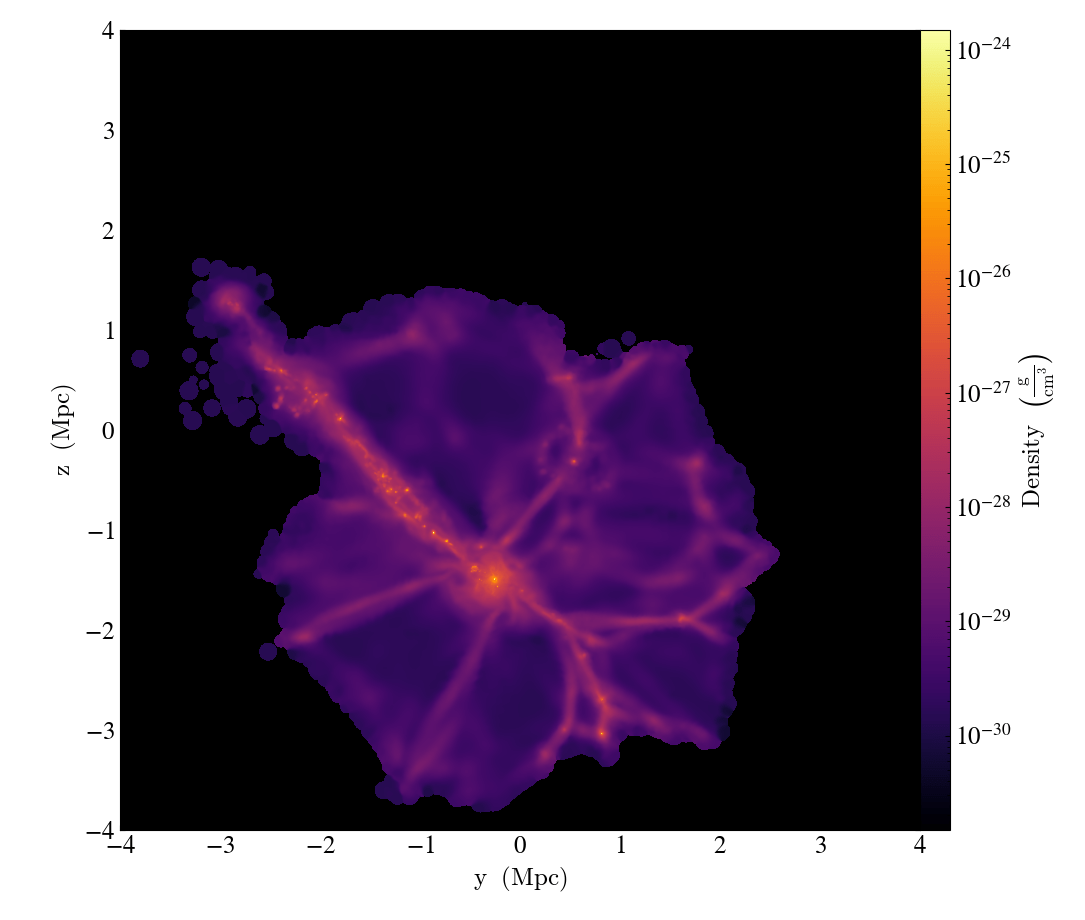
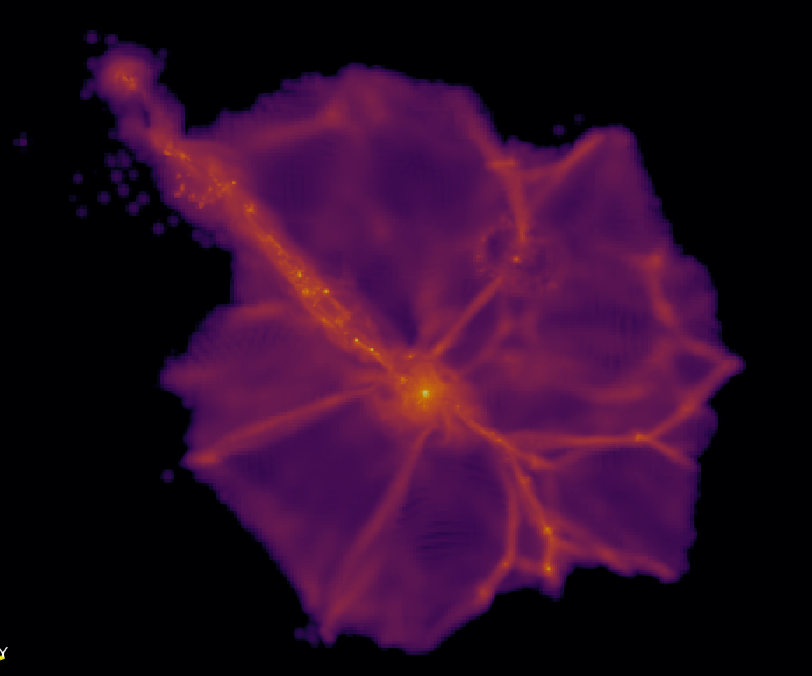
AGORA Isolated Disk test
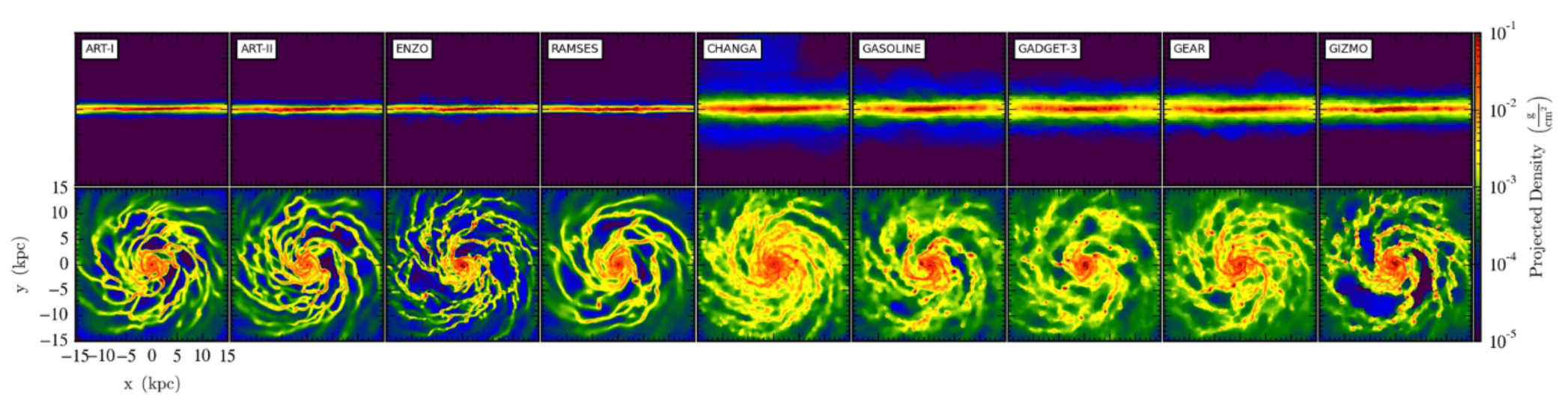
Kim+16
- \(10^{12}\,M_\odot\) live-halo
- \(3.5\times 10^{10}\,M_\odot\) stellar disk (+ bulge)
- \(8.6 \times10^{9}\,M_\odot\) gas disk
- Pressure floor at \(T\sim1800\,\mathrm{K}\)
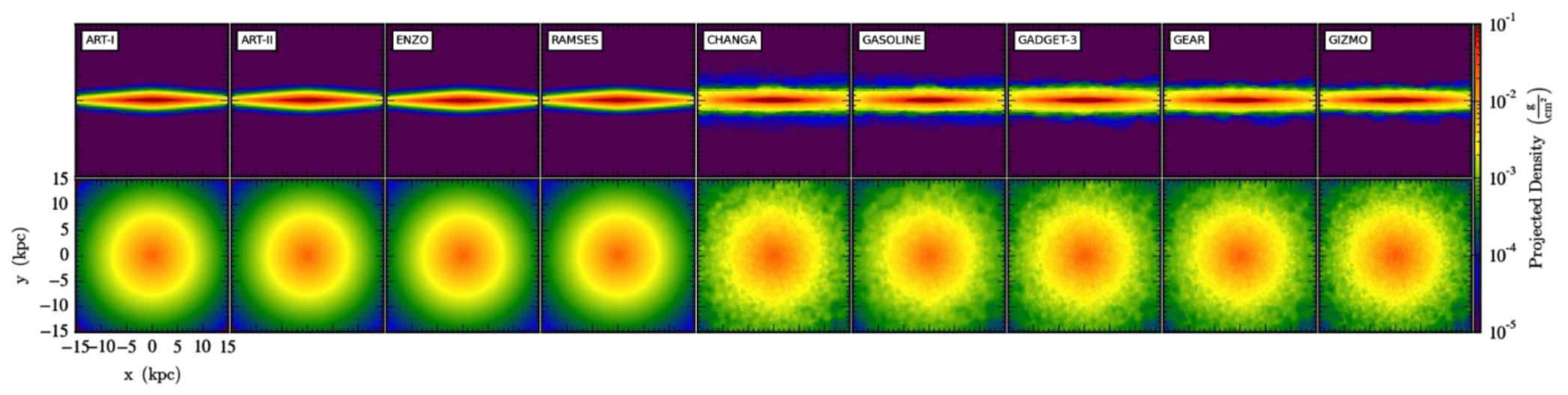
\(+500\,\mathrm{Myr}\)
AGORA Isolated Disk test
Implementation in Dyablo:
- Cooling using tables from Grackle (UVB + metals),
- Assume \(Z=Z_\odot\),
- \(T_\mathrm{min} = 2.725\,\mathrm{K}\) (CMB temperature),
- \(\dfrac{\mathrm{d}\rho_\star}{\mathrm{d}t} = \varepsilon_\star \dfrac{\rho_\mathrm{gas}}{t_\mathrm{ff}}\)
- \(10\%\) of star mass goes SNII
\(10^{51}\,\mathrm{erg}\) per SNII (thermal), after \(10\,\mathrm{Myr}\)
Disk ICs
Refinement on mass
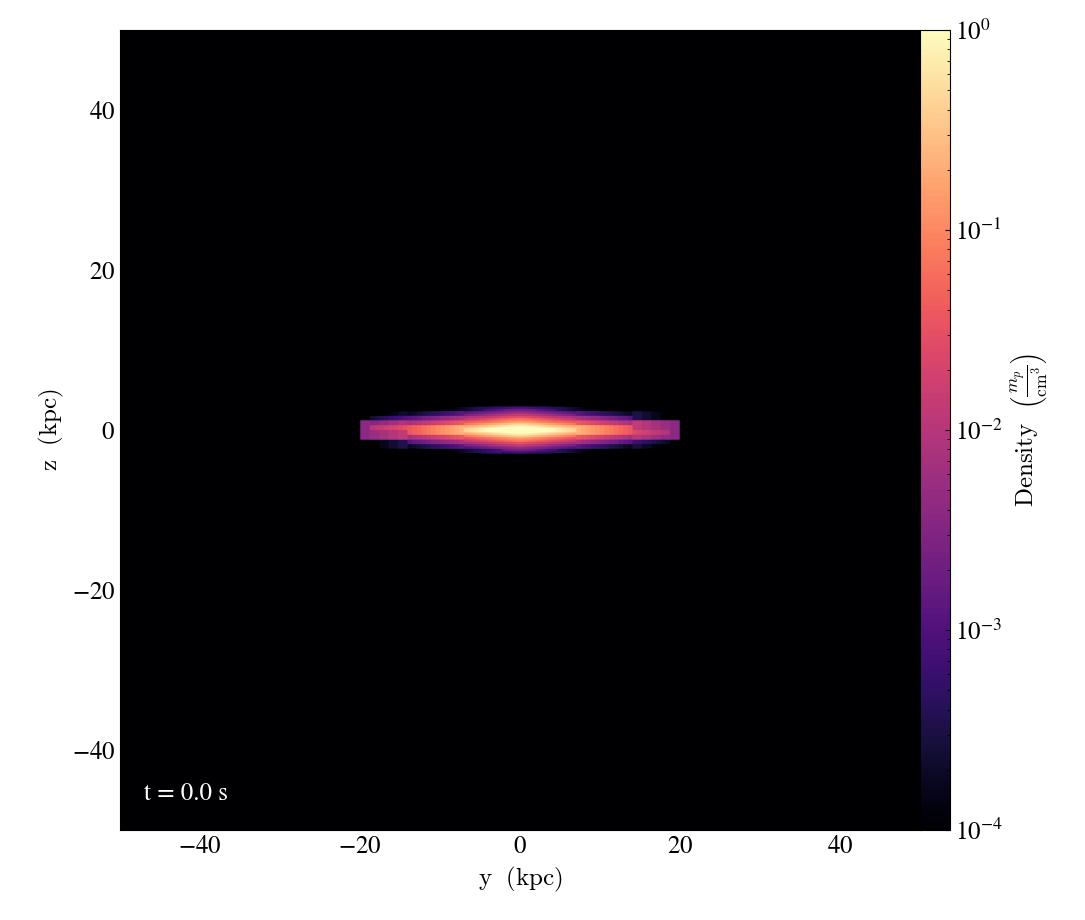
Disk does not fragment? → pressure floor?
Agora's P-\(\rho\) is bizarre

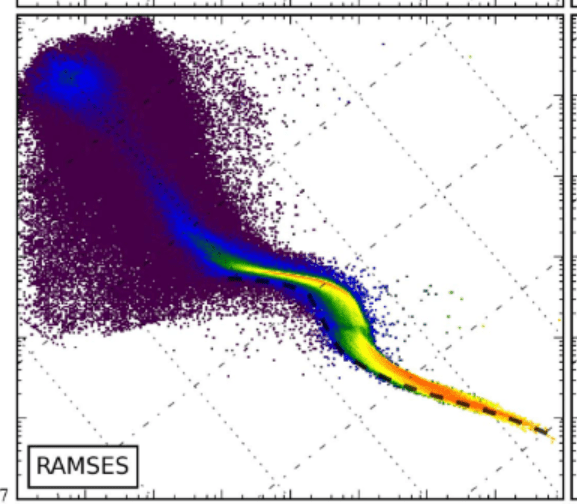
AGORA Isolated Disk test
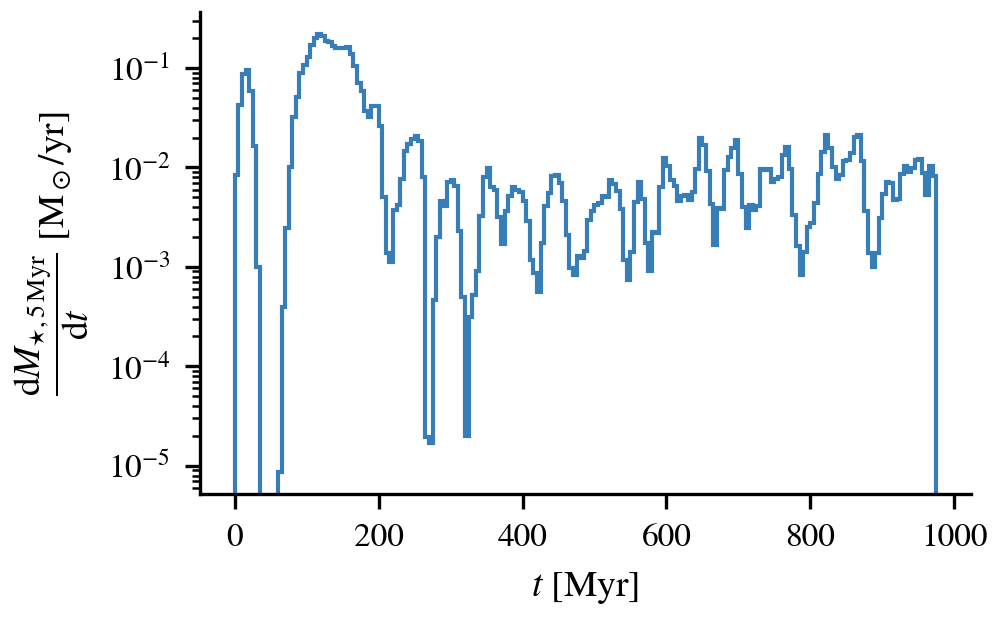
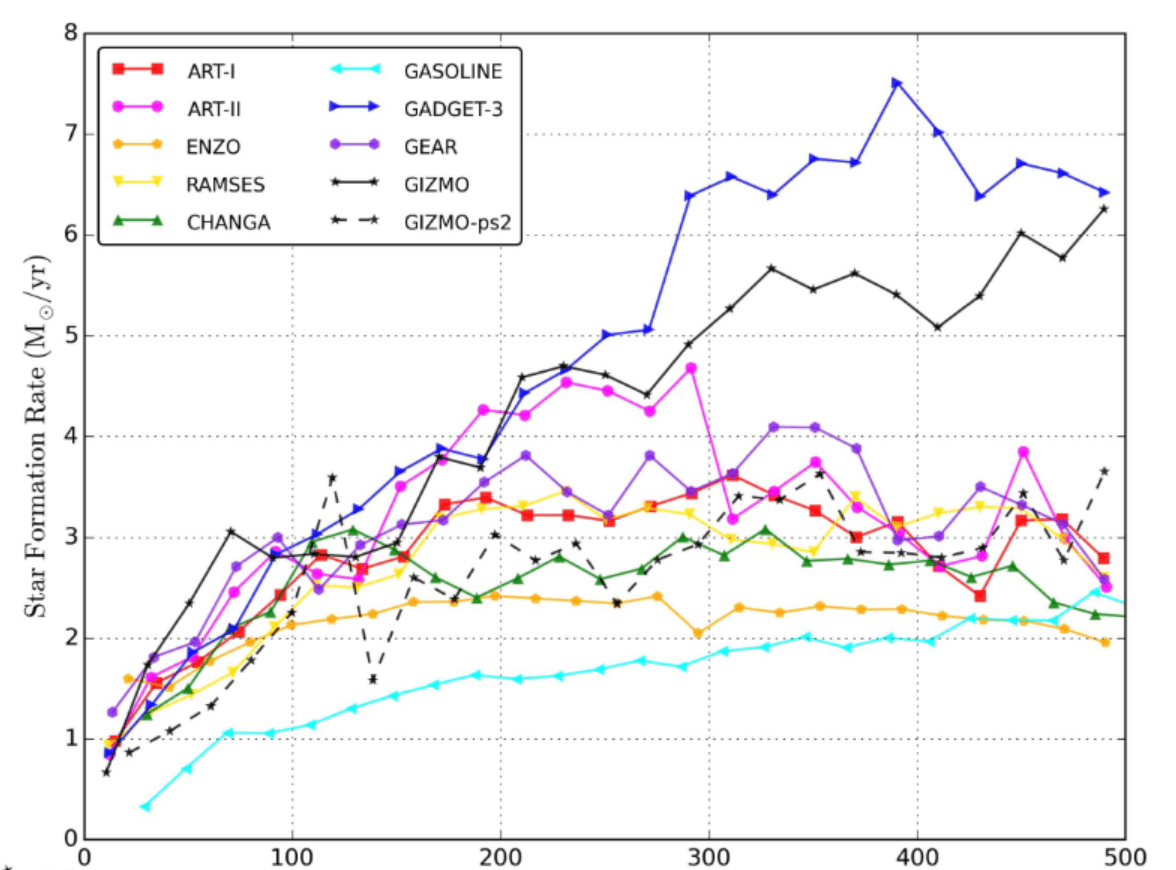
Star formation too low? Too stochastic?
Why the bump in first \(200\,\mathrm{Myr}\)?
AGORA Isolated Disk test
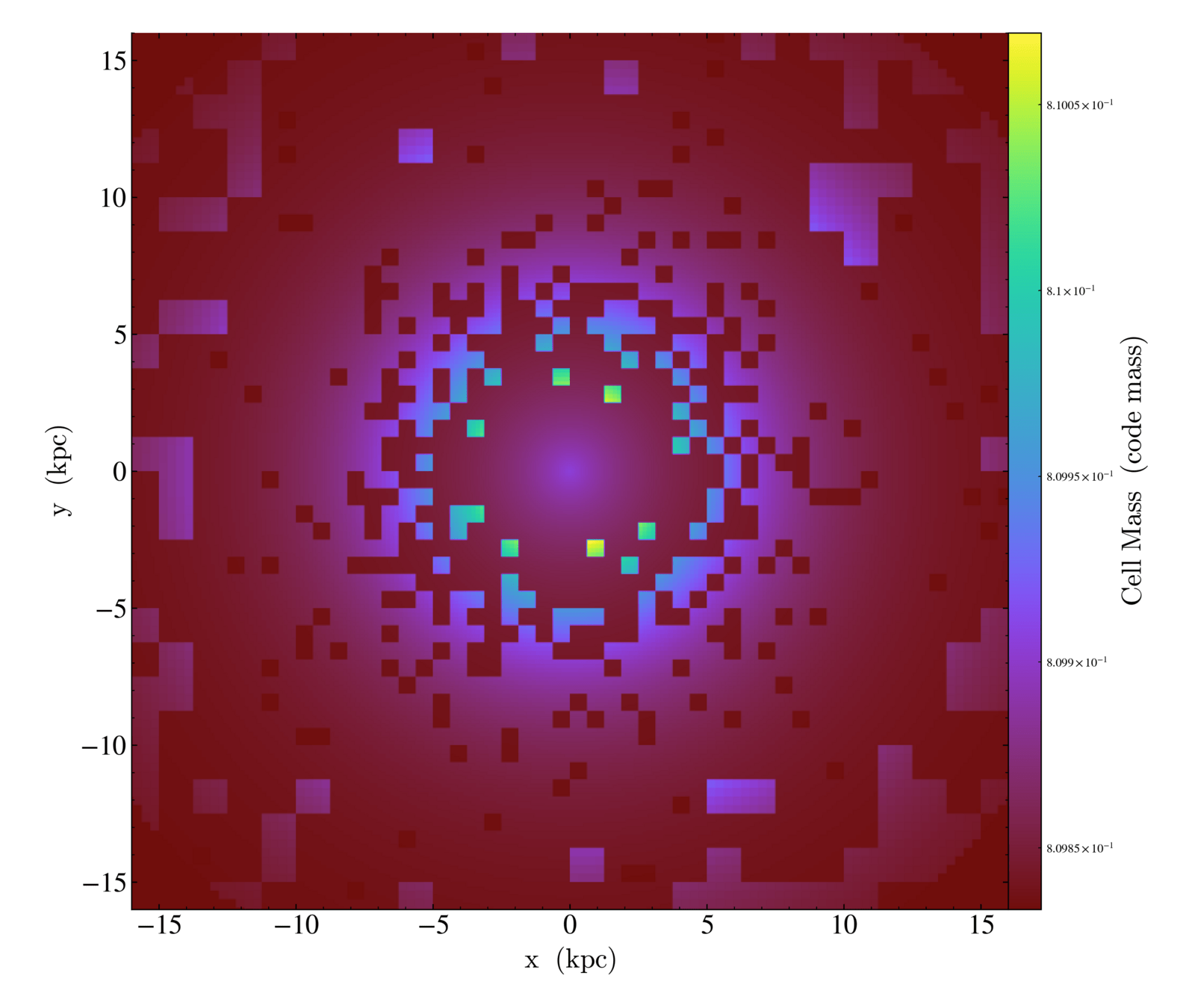
Some artifacts in cell masses:
true or plotting artefacts?
With mechanical feedback (Kimm & Cen 2014)
Slice
Projection
Note:
From Megatron to Gigatron
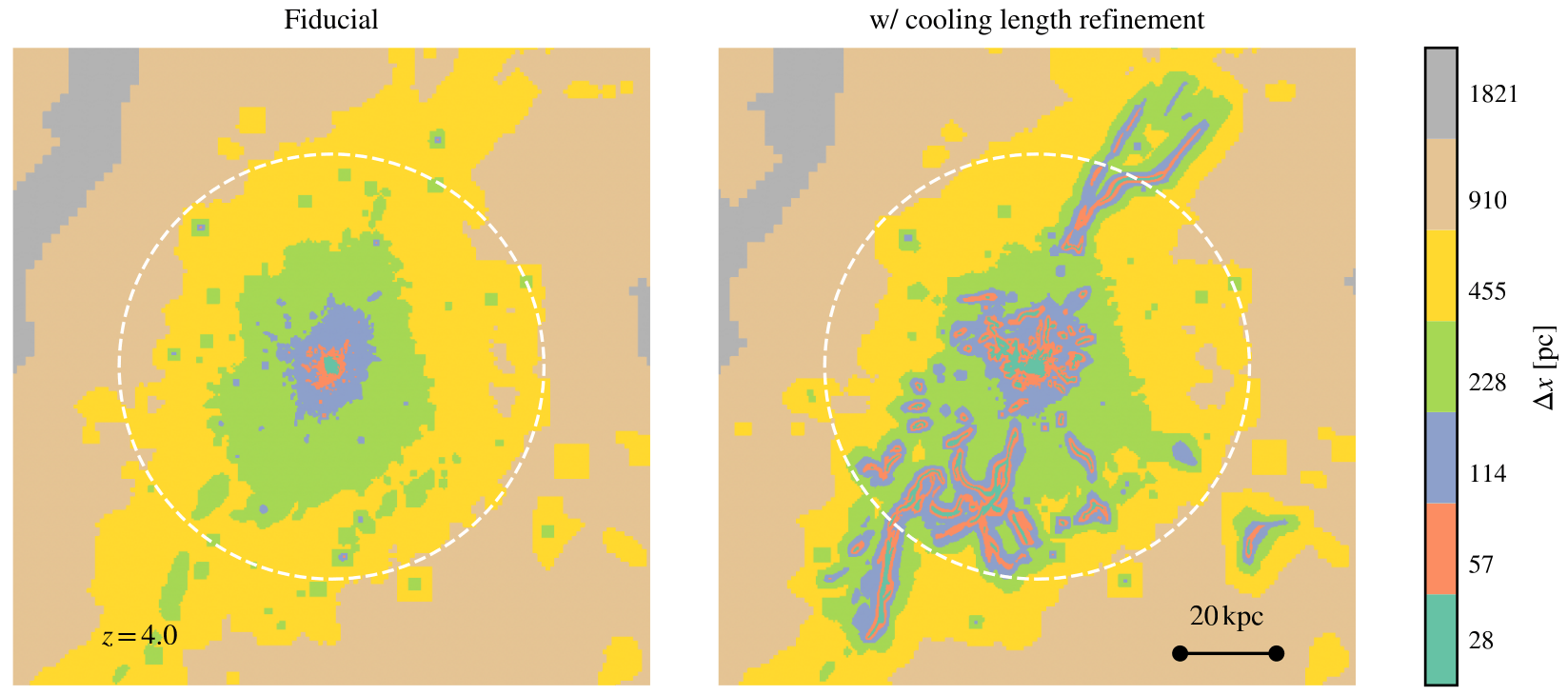
→ 30 pc in the CGM
