Almost tight \(\ell\)-covering of \(\mathbb{Z}_n\)

Ke Shi

Chao Xu

Flash Memory Storage

state \(\in \{0,\ldots,\ell\}\)

cell stores a state

block \(\sim 10^6\) cells

Operations

increase a state

= single cell update

set a state to 0

= clear entire block

Abstract memory cell (AMC): stores a value in \(\N\)

- Read: read the number in the cell

- Update: increase the cell by a number in \(\{0,\ldots,\ell\}\)

\(\Z_n=\{0,1,2,\ldots,n-1\}\)

Store and rewrite a number in \(\Z_n\)

1 rewrite = 1 AMC update

Store a number in \(\Z_n\) use AMCs

store \(y\in \Z_n\) by storing \(x\in \N^t\)

\(s\in \Z_n^t\) a fixed vector

D(x) = s\cdot x \pmod n = y

\(2\)

\(4\)

\(3\)

\(1\)

\(D(x) = (1,2,3,4) ·(1,7,2,9)\pmod{12} =9\)

Example:

AMC storage

t=4

n=12

y=9

s=(1,7,2,9)

1 rewrite = 1 AMC update

\(D(x) = (1,2,3,4) ·(1,7,2,9)\pmod{12} =9\)

Example:

AMC storage

t=4

n=12

y=9

s=(1,7,2,9)

\(D(x) = (1,2,{\color{red}5},4) ·(1,7,2,9)\pmod{12} ={\color{red}1}\)

\(2\)

\(4\)

\(3\)

\(1\)

\(5\)

1 AMC update per rewrite is possible if and only if

\displaystyle \Z_n = \bigcup_{i\in s}\{ei\pmod{n} | e\leq \ell\}

x_j\gets x_j + e \Leftrightarrow y \gets y+e s_j\pmod{n}

y={\color{red}1}

1 rewrite = 1 AMC update

1 AMC update per rewrite is possible if and only if

\displaystyle \Z_n = \bigcup_{i\in s}\{ei\pmod{n} | e\leq \ell\}

\(t\) should be as small as possible to save space

For a fixed \(\ell\) and \(n\), how large must \(t\) be?

\(\ell\)-covering

S_i^{\ell} = \{0i,1i,2i,\ldots, \ell i\}

\(A\subseteq \mathbb{Z}_n\) is a \(\ell\)-covering of \(U\),

If \(U\subseteq \bigcup_{i\in A} S_i^{\ell}\).

\(U=\Z_n\) most of the time.

We omit \(\ell\) when it is clear

A segment of length \(\ell\) with slope \(i\).

Find a small \(\ell\)-covering \(A\subseteq \mathbb{Z}_n\)

\(n=7, \ell=3\)

\(S_1\)

\(S_3\)

\(S_4\)

\(\mathbb{Z}_n\)

\(S_2\)

\(S_5\)

\(S_6\)

\(5\)

\(4\)

\(6\)

\(0\)

\(1\)

\(3\)

\(5\)

\(0\)

\(1\)

\(4\)

\(5\)

\(0\)

\(3\)

\(2\)

\(6\)

\(0\)

\(2\)

\(4\)

\(6\)

\(0\)

\(1\)

\(3\)

\(2\)

\(0\)

\(1\)

\(3\)

\(2\)

\(4\)

\(5\)

\(6\)

\(0\)

\(S_0\)

\(0\)

\(n=7, \ell=3\)

\(\mathbb{Z}_n\)

\(1\)

\(4\)

\(5\)

\(0\)

\(3\)

\(2\)

\(6\)

\(0\)

\(1\)

\(3\)

\(2\)

\(4\)

\(5\)

\(6\)

\(0\)

\(A=\{3,4\}\)

\(A\)

\(S_3\)

\(S_4\)

Find a small \(\ell\)-covering \(A\subseteq \mathbb{Z}_n\)

\(n=7, \ell=3\)

\(\mathbb{Z}_n\)

\(1\)

\(4\)

\(5\)

\(0\)

\(3\)

\(2\)

\(6\)

\(0\)

\(1\)

\(3\)

\(2\)

\(4\)

\(5\)

\(6\)

\(0\)

\(f(n,\ell)\) is the size of the smallest \(\ell\)-covering of \(\mathbb{Z}_n\).

\(f(7,3)\leq |A| = 2\)

\left\lceil \frac{n-1}{\ell} \right\rceil \leq f(n,\ell) \leq n-1

\( 2 = \left\lceil \frac{7-1}{3} \right\rceil \leq \)

\(A=\{3,4\}\)

Find a small \(\ell\)-covering \(A\subseteq \mathbb{Z}_n\)

Main Questions

Combinatorial: What is the correct bound for \(f(n,\ell)\)?

Algorithmic: How to find a small \(\ell\)-covering?

\(f(n,\ell)=\left\lceil \frac{n-1}{\ell} \right\rceil\)?

No.

\(f(16,5)>3=\lceil \frac{16-1}{5}\rceil\)

Klove et. al. multiple papers in the 2010s: \(f(n,\ell)\) for \(\ell=2,3,4\)

Chen et. al. 2013: \(f(n,\ell) \leq \frac{n^{1+o(1)}}{\sqrt{\ell}}\)

Previous Work

\(f(n,\ell) = O(\frac{n}{\ell}\log n\log \log n)\)

if \(\ell\) is neither too small nor too large

n^{\Omega(\frac{1}{\log \log n})} \leq \ell \leq n^{1-\Omega(\frac{1}{\log \log n})}

Koiliaris & Xu 2019

Our results

\(f(n,\ell) = O(\frac{n}{\ell}\log n\log \log n)\)

A \(O(f(n,\ell)\log n)\) size \(\ell\)-covering can be found in time

\(\tilde{O}(\frac{n}{\ell}) + n^{o(1)}\)

There exist examples where

\(f(n,\ell)=\Omega(\frac{n}{\ell}\frac{\log n}{\log \log n})\)

\(f(n,\ell) = O(\frac{n}{\ell}\log n\log \log n)\)

* \(\ell\) is not too small and not too large.

A more refined analysis of \(\varphi(n,\ell)\).

A more refined analysis of covering.

\displaystyle\varphi(n,\ell)=\sum_{\substack{ x\leq\ell \\ \gcd(x,n)=1}}1

\varphi(n)=\varphi(n,n)

Set cover

Given \(\mathcal{S} \subseteq 2^U\).

A collection of sets in \(\mathcal{S}\) covers \(U\) is a set cover.

Formally, if \(\mathcal{S}'\subseteq \mathcal{S}\) such that \(U= \bigcup_{X\in \mathcal{S}'} X\), then \(\mathcal{S}'\) is a set cover of \(U\).

\(\ell\)-covering as set cover

\(U=\Z_n\)

\(S_i=\{ij\pmod{n}|j\leq\ell\}\)

\(\mathcal{S}=\{S_i|i\in\Z_n\}\)

An algebraic special case

Each elements covered by \(b\) sets

\(O\left(\frac{|\mathcal{S}|}{b}\log \ell\right)\) size set cover

(naively) apply to \(\ell\)-covering?

\begin{aligned} &\Z_{n,d}&&=&&\{x|\gcd(x,n)=d,x\in\Z_n\} \\ &\Z_n^*&&=&&\Z_{n,1} \end{aligned}

\(p\) a large prime, \( n=2p, \ell=p-1\). \(p\) only covered by \(S_p\).

No

\(f^*(n,\ell)\) the smallest \(\ell\)-covering of \(\Z^*_n\) such that all segments has slope in \(\Z^*_n\).

Covering \(\Z_n^*\) with \(\Z_n^*\) slope segments

Every elment in \(\Z^*_n\) is covered by \(\varphi(n,\ell)\) segments with slope in \(\Z^*_n\).

Previous bound for \(\varphi(n,\ell)\)

\varphi(n,\ell) = \begin{cases} \Omega(\frac{\ell}{n} \varphi(n))& \text{ if } \ell > n^{\Omega(\frac{1}{\log \log n})}\\ \Omega(\frac{\ell}{\log \ell}) & \text{ if } \ell > c \log n\\ \end{cases}

Constants \(c,u\geq 1\)

\varphi(n,\ell) = \begin{cases} \Omega(\frac{\ell}{n} \varphi(n))& \text{ if } \ell > n^{\Omega(\frac{1}{\log \log n})}\\ \Omega(\frac{\ell}{\log \ell}) & \text{ if } \ell > c \log n\\ \end{cases}

c \log^u n

Previous bound for \(\varphi(n,\ell)\)

Case 1: \(\ell > c \log^u n\)

Sieve Theory

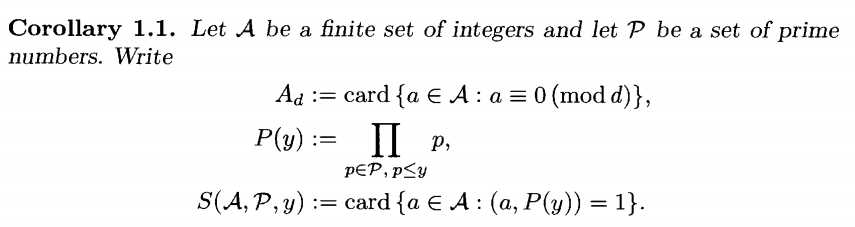
\(\pi(\ell)\geq c_1\frac{\ell}{\log \ell}\) (Prime Number Theorem)

\(\omega(n)\leq c_2\frac{\log n}{\log \log n}\).

\(\omega(n)\leq \frac{\pi(\ell)}{2} \) if \(\ell \geq c\log n\) for sufficiently large \(n\).

Case 2: \(\ell > c \log n\)

\varphi(n,\ell)\geq \pi(\ell)-\omega(n)

\(\pi(n)\): number of primes no larger than \(n\)

\(\omega(n)\): number of distinct prime factors of \(n\)

\varphi(n,\ell)=\Omega\left(\frac{\ell}{\log \ell}\right)

Bound for \(f^*(n,\ell)\)

f^*(n,\ell) = O\left(\frac{n}{\ell}\log n\right)

Using the fact about \(\varphi(n,\ell)\).

Case 1: \(\ell > c \log^u n\)

\begin{aligned} f^*(n,\ell) &= O\left(\frac{\varphi(n)\log \ell}{\frac{\ell}{n}\varphi(n)}\right)\\ &= O\left(\frac{n}{\ell}\log n\right) \end{aligned}

\text{each element covered by } b \text{ sets} \Rightarrow O(\frac{|S|\log \ell}{b})

\varphi(n,\ell) = \Omega(\frac{\ell}{n}\varphi(n))

\begin{aligned} f^*(n,\ell) &= O\left(\frac{\varphi(n)\log \ell}{\frac{\ell}{\log \ell}}\right)\\ &= O\left(\frac{\varphi(n)}{\ell}(\log \ell)^2\right) \\ &= O\left(\frac{n}{\ell}(\log \log n)^2\right)\\ &= O\left(\frac{n}{\ell}\log n\right) \end{aligned}

Case 2: \(c\log n<\ell < c \log^u n\)

O(\frac{|S|\log \ell}{b})

\varphi(n,\ell) = \Omega(\frac{\ell}{\log \ell})

\ell = O(\log^u n)

\begin{aligned} f^*(n,\ell)&\leq \varphi(n) \\ &= O\left(\varphi(n)\frac{\log n}{\ell}\right) \\ &= O\left(\frac{n}{\ell}\log n\right) \end{aligned}

Case 3: \(\ell < c \log n\)

We can cover \(\mathbb{Z}_{n,d}\) with \(f^*(\frac{n}{d},\ell) \) segments in \(\mathbb{Z}_{n,d}\).

We can cover \(\mathbb{Z}_n^*\) with \(f^*(n, \ell)\) segments in \(\mathbb{Z}_n^*\).

\(\mathbb{Z}_n\)

We can cover \(\mathbb{Z}_{n,d}\) with \(f^*(\frac{n}{d},\ell) \) segments in \(\mathbb{Z}_{n,d}\).

\(\mathbb{Z}_n\)

\(d \mid x\)

We can cover \(\mathbb{Z}_n^*\) with \(f^*(n, \ell)\) segments in \(\mathbb{Z}_n^*\).

We can cover \(\mathbb{Z}_{n,d}\) with \(f^*(\frac{n}{d},\ell) \) segments in \(\mathbb{Z}_{n,d}\).

\(\mathbb{Z}_n\)

\(d \mid x\)

\(\mathbb{Z}_{n,d}\)

We can cover \(\mathbb{Z}_n^*\) with \(f^*(n, \ell)\) segments in \(\mathbb{Z}_n^*\).

We can cover \(\mathbb{Z}_{n,d}\) with \(f^*(\frac{n}{d},\ell) \) segments in \(\mathbb{Z}_{n,d}\).

\(\mathbb{Z}_n\)

\(d \mid x\)

\(\mathbb{Z}_{n,d}\)

\(\mathbb{Z}^{*}_{\frac{n}{d}}\)

We can cover \(\mathbb{Z}_n^*\) with \(f^*(n, \ell)\) segments in \(\mathbb{Z}_n^*\).

Cover of \(\Z^*_\frac{n}{d}\) using \(\Z^*_{\frac{n}{d}}\) lifts to a cover of \(\Z_{n,d}\) using \(\Z_{n,d}\)

\mathbb{Z}^*_{12}

\mathbb{Z}_{12,2}

\mathbb{Z}_{12,3}

\mathbb{Z}_{12,4}

\mathbb{Z}_{12,6}

\mathbb{Z}_{12,12}

f^*(12,4)

\ell=4

\mathbb{Z}^*_{12}

\mathbb{Z}_{12,2}

\mathbb{Z}_{12,3}

\mathbb{Z}_{12,4}

\mathbb{Z}_{12,6}

\mathbb{Z}_{12,12}

f^*(12,4)

f^*(6,4)

\ell=4

\mathbb{Z}^*_{12}

\mathbb{Z}_{12,2}

\mathbb{Z}_{12,3}

\mathbb{Z}_{12,4}

\mathbb{Z}_{12,6}

\mathbb{Z}_{12,12}

f^*(12,4)

f^*(6,4)

f^*(3,4)

f^*(4,4)

f^*(2,4)

f^*(1,4)

f(12,4)

\leq

\ell=4

Bound for \(f(n,\ell)\)

\(d(n) = n^{O\left(\frac{1}{\log \log n}\right)}\)

\(\sigma(n) = O(n\log \log n)\)

f(n,\ell) \leq \sum_{d|n} f^*(\frac{n}{d},\ell)

\leq \sum_{d|n} \max(d \frac{\log n}{\ell},1)

\leq \sigma(n)\frac{\log n}{\ell} + d(n)

= \underbrace{ O\left(\frac{n}{\ell}\log n\log \log n\right)}_{\textbf{main term}} + {\color{red}\underbrace{n^{O\left(\frac{1}{\log \log n}\right)}}_{\textbf{error term}}}

Desired bound unless \(\ell\) is too large.

f^*(n,\ell) = O(\frac{n}{\ell}\log n)

\mathbb{Z}^*_{12}

\mathbb{Z}_{12,2}

\mathbb{Z}_{12,3}

\mathbb{Z}_{12,4}

\mathbb{Z}_{12,6}

\mathbb{Z}_{12,12}

Larger Cover

\(\ell = 4\)

Theorem:

If \(\ell\) is large, \(d\leq \ell'\), then each element in \(\Z_{n,d}\) is covered \(\Omega(\frac{\ell}{n}\varphi(n))\) times by segments with slope in \(\Z^*_n\).

\ell' := \frac{\ell}{c \log^u \frac{n}{\ell}}

Theorem:

If \(\ell\) is large, each element in \(\Z^*_n\) is covered \(\Omega(\frac{\ell}{n}\varphi(n))\) times by segments with slope in \(\Z^*_n\).

\(f^\dagger(n,\ell)\) the smallest \(\ell\)-covering of \(\bigcup_{d|n,d\leq \ell'} \Z_{n,d}\) such that all segments has slope in \(\Z^*_n\).

f^\dagger(n,\ell) = O(\frac{n}{\ell}\log n)

f^*(n,\ell) = O(\frac{n}{\ell}\log n)

What's the relation between \(f(n,\ell)\) and \(f^\dagger(n,\ell)\)?

\displaystyle f(n,\ell) \leq \sum_{d|m} f^\dagger(\frac{n}{d},\ell)

\displaystyle n = \prod_{i=1}^k p_i

\displaystyle m = \prod_{i=1}^j p_i \geq \frac{n}{\ell'}

If \(d|n\), then \(d=d_1d_2\), where \(d_1|m\), and \(d_2\leq \ell'\).

How large is \(d(m)\)?

\begin{aligned} &\leq \sum_{d|m}O\left(\frac{n}{d}\frac{\log n}{\ell} \right)+1\\ &\leq O\left(\sigma(n)\frac{\log n}{\ell}\right) + d(m) \end{aligned}

d(n) = n^{O(\frac{1}{\log \log n})}

d(m)

\leq 2d(m')

=m'^{O(\frac{1}{\log \log m'})}

= \left(\frac{n}{\ell}\log^u \frac{n}{\ell}\right)^{O\left(\frac{1}{\log \log \frac{n}{\ell}}\right)}

= \frac{n}{\ell} c\log^u \frac{n}{\ell}

< \frac{n}{\ell'}

m':=\frac{m}{p_j}

\begin{aligned} f(n,\ell) &\leq \sum_{d|m} f^\dagger(\frac{n}{d},\ell)\\ &\leq \sum_{d|m}O\left(\frac{n}{d}\frac{\log n}{\ell} \right)+1\\ &\leq O\left(\sigma(n)\frac{\log n}{\ell}\right) + d(m)\\ &= \underbrace{ O\left(\frac{n}{\ell}\log n\log \log n\right)}_{\textbf{main term}} + {\color{red} \underbrace{\left(\frac{n}{\ell}\log^u \frac{n}{\ell}\right)^{O\left(\frac{1}{\log \log \frac{n}{\ell}}\right)}}_{\textbf{error term}}}\\ &= O\left(\frac{n}{\ell}\log n\log \log n\right) \end{aligned}

\(f(n,\ell) = O(\frac{n}{\ell}\log n\log \log n)\)

Conclusion and Future Work

Better bound for \(f(n,\ell)\)?

What about \(\ell\)-covering of arbitrary set \(X\subseteq \Z_n\)?

Other interesting groups, e.g. \(\Z_n\times \Z_m\).

IP

\begin{aligned} & \min_{x} & & \sum_{i} x_i & \\ & \text{s.t.} & & \sum_{i:j\in i[\ell]} x_i\geq 1 & j\in \Z_n \\ & & & x_i \in \{0,1 \} & i\in \Z_n \\ \end{aligned}

Integer programming form of set cover

LP (Relaxation)

\begin{aligned} & \min_{x} & & \sum_{i} x_i & \\ & \text{s.t.} & & \sum_{i:j\in i[\ell]} x_i\geq 1 & j\in \Z_n \\ & & & 0 \leq x_i & i\in \Z_n \\ \end{aligned}

Symmetric LP

A linear program is symmetric if there exists a permutation of variables, so the linear program does not change it's value.

\begin{bmatrix} x_1 \\ x_2 \\.\\.\\.\\x_n \end{bmatrix} \xRightarrow[\textbf{permutation group G}]{\forall \textbf{permutation } \pi \text{ in}} \begin{bmatrix} x_{\pi(1)} \\ x_{\pi(2)} \\.\\.\\.\\x_{\pi(n)} \end{bmatrix}

\(\textbf{fesible}\) \(\xRightarrow[\textbf{ }]{}\) \({}\textbf{fesible}\)

\(\textbf{c}\cdot\textbf{x}\) \(\xRightarrow[\textbf{ }]{\textbf{same value}}\) \(\textbf{c}\cdot\pi\textbf{ x}\)

We call such a LP \(G\)-symmetric.

Reduce variables

Let \(G\) be a permutation group that consists of all permutations that swaps \(i\) and \(j\) if \(\gcd(i,n)=\gcd(j,n)\). LP2 is \(G\)-symmetric.

\begin{aligned} \{x_i:i\in \Z_n\}&\longrightarrow &&\{y_d:d|n\}\\ \text{number:}\quad n&\longrightarrow &&d(n) \end{aligned}

We let \(y_d\) to represent all variables in \(\{x_i|\gcd(i,n)=d\}\).

Reduce constraints

If \(\gcd(a,n) = \gcd(b,n)\), then the constraints that covers \(a\) and \(b\) have same format since all variables \(y_d\) have same coffcients in inequalities \(a\) and \(b\).

\begin{aligned} \{\mathrm{constraint}_i:i\in \Z_n\}&\longrightarrow &&\{\mathrm{constraint}_d:d|n\}\\ n&\longrightarrow &&d(n) \end{aligned}

LP (compact)

\begin{aligned} & \min_{y} & & \sum_{d:d|n} \varphi(\frac{n}{d}) y_d & \\ & \text{s.t.} & & \sum_{d:d|c} \frac{\varphi(n/c, d \ell / c)\varphi(n/d)}{\varphi(n/c)} y_d\geq 1 & c|n \\ & & & 0\leq y_d & d|n \\ \end{aligned}

We have only \(d(n)\) variables and inequalities now!

\begin{aligned} & \min_{y} & & \sum_{d:d|n} \color{red}{\varphi(\frac{n}{d}) y_d} & \\ & \text{s.t.} & & \sum_{d:d|c} \frac{\varphi(n/c, d \ell / c)\color{red}{\varphi(n/d)}}{\varphi(n/c)} {\color{red}y_d} \geq 1 & c|n \\ & & & 0\leq y_d & d|n \\ \end{aligned}

LP*

\begin{aligned} & \min_{d} & & \sum_{d:d|n} u_d & \\ & \text{s.t.} & & \sum_{d:d|c} \frac{\varphi(n/c, d \ell / c)}{\varphi(n/c)} u_d\geq 1 & c|n \\ & & & 0\leq u_d & d|n \end{aligned}

Let \(u_d=\varphi(n/d)y_d\), We have the following concise form.

Randomized algorithm

\(\underline{\textbf{Cover}(n,\ell)}\)

compute the prime factorization of \(n\)

compute \(\varphi(n/c,d\ell/c)\) and \(\varphi(n/c)\) for all \(d|c|n\)

compute the optimum for \(\mathrm{LP4}\)

\(C\leftarrow \empty\)

repeat \(4\log{n}\) times

for \(d|n\):

if \(u_d\geq1\):

\(C\leftarrow C\cup (S\sim {\Z_{n,d}\choose \lceil u_d \rceil})\)

else if \(u_d > (x\sim[0,1])\):

\(C\leftarrow C\cup (S\sim {\Z_{n,d}\choose 1})\)

return \(C\)

taking \(O(f(n,\ell)\mathrm{ploylog}(n)) \) time

taking \(n^{o(1)}\) time

Theorem:

Algorithm before takes \(O(f(n,\ell)\mathrm{polylog} n + n^{o(1)})\) time and computes a expected size \(O(f(n,\ell)\log n)\) \(\ell\)-covering set in expectation with constant probability.

Theorem: There is an algorithm which successfully returns \(X\sim {\Z^*_n \choose k}\) in \(O(k \mathrm{polylog}(n))\) time with probability at least \(1-\frac{1}{n}\).

Sampling in \(\Z_n^*\)

Running time analysis

Time of constructing the LP.

Step 1. Finding the prime factorization of \(n\) takes \(n^{o(1)}\) time through general number field sieve.

Step 2. Computing all \(\varphi(n/c),c|n\) through \(\varphi(n)=n\prod_{p|n}(1-1/p)\) takes \(n^{o(1)}\) time.

Sampling in \(\Z_n^*\)

Otherwise, \(k<\frac{\varphi(n)}{2}\). We will sample a random element \(x\sim \Z_n\), if \(x\in\Z_n^*\) and we hasn't get enough elements, pick it. Repeat it specific times.

We can show the runing time of the algorithm is \(O(k \mathrm{polylog}(n))\) and Chernoff bound can show the success probability at least \(1-\frac{1}{n}\).

Consider two cases. If \(k\geq \frac{\varphi(n)}{2}\), then find all elements in \(\Z_n^*\) by brute force and pick \(k\) from it.

Running time analysis

Step 3. Computing all \(\varphi(n/c,d\ell/c),d|c|n\) through the inclusion-exclusion principle takes \(n^{o(1)}\) time.

\varphi(n,\ell) = \sum_{i=0}^{\omega(n)} (-1)^{i} \sum_{S\subset P, |S|=i} \left\lfloor\frac{\ell}{\prod_{p\in S} p} \right\rfloor

The running time of computing \(\varphi(n,\ell)\) is \(\tilde{O}(2^{\omega(n)})=n^{O(\frac{1}{\log\log n})}=n^{o(1)}\). The number of all \((c,d)\) is also \(n^{o(1)}\).

Running time analysis

The total time of sampling is :

\(O(\sum_{d|n}u_d \mathrm{polylog}n)=O(f(n,\ell)\mathrm{ploylog}(n)) \).

Combining all above, the algorithm takes \((O(f(n,\ell)\mathrm{ploylog}(n)+n^{o(1)})\) time.

Thank you

Limited-magnitude errors:

Jiang A., Langberg M., Schwartz M., Bruck J.: Trajectory codes for flash memory. IEEE Trans. Inf. Theory 59(7), 4530–4541 (2013).

Sieve theory:

Alina Carmen Cojocaru, M Ram Murty, et al. An introduction to sieve methods and their applications, volume 66. Cambridge University Press, 2006.

References