Almost tight \(\ell\)-covering of \(\mathbb{Z}_n\)

Ke Shi

Chao Xu

cxu@uestc.edu.cn

博士生，硕士生
博士后
助理教授（50w+年薪）

电子科技大学

理论计算机科学团队

https://tcsuestc.com/

逻辑，组合优化，图论，机制设计，计算代数，实验算法，精确算法，分配机制，算法博弈论

Flash Memory Storage

state \(\in [\ell]=\{0,\ldots,\ell\}\)

cell stores a state

block \(\sim 10^6\) cells

Operations

increase a state

= single cell update

set a state to 0

= clear entire block

write \(10^6\) cells

Cell stores a value in \(\N\)

- Read: read the number in the cell

- Increase: increase the cell by a number in \([\ell]\)

A simpler increment only model

\(\Z_n=\{0,1,2,\ldots,n-1\}\)

Store and update a number in \(\Z_n\)

1 update = 1 cell increase

Store a number in \(\Z_n\)

store \(y\in \Z_n\) by storing \(x\in \N^t\)

\(s\in \Z_n^t\) a fixed vector

D(x) = s\cdot x \pmod n = y

\(2\)

\(4\)

\(3\)

\(1\)

\(D(x) = (1,2,3,4) ·(1,7,2,9)\pmod{12} =9\)

Example:

Cell storage

t=4

n=12

y=9

s=(1,7,2,9)

1 update = 1 cell increase

\(D(x) = (1,2,3,4) ·(1,7,2,9)\pmod{12} =9\)

Example:

t=4

n=12

y=9

s=(1,7,2,9)

\(D(x) = (1,2,{\color{red}5},4) ·(1,7,2,9)\pmod{12} ={\color{red}1}\)

\(2\)

\(4\)

\(3\)

\(1\)

\(5\)

1 increase per update is possible if and only if

\displaystyle \Z_n = \bigcup_{i\in s}\{ei\pmod{n} | e\in [\ell]\}

x_j\gets x_j + e \Leftrightarrow y \gets y+e s_j\pmod{n}

y={\color{red}1}

Cell storage

\(t\) should be as small as possible to save space

For a fixed \(\ell\) and \(n\), how large must \(t\) be?

1 increase per update is possible if and only if

\displaystyle \Z_n = \bigcup_{i\in s}\{ei\pmod{n} | e\in [\ell]\}

1 update = 1 cell increase

\(\ell\)-covering

S_i^{\ell} = \{0i,1i,2i,\ldots, \ell i\}

\(B\subseteq \mathbb{Z}_n\) is a \(\ell\)-covering of \(U\),

If \(U\subseteq \bigcup_{i\in B} S_i^{\ell}\)

We omit \(\ell\) when it is clear

A segment of length \(\ell\) with slope \(i\).

Find a small \(\ell\)-covering \(B\subseteq \mathbb{Z}_n\)

\(n=7, \ell=3\)

\(S_1\)

\(S_3\)

\(S_4\)

\(\mathbb{Z}_n\)

\(S_2\)

\(S_5\)

\(S_6\)

\(1\)

\(4\)

\(6\)

\(0\)

\(1\)

\(3\)

\(5\)

\(0\)

\(1\)

\(4\)

\(5\)

\(0\)

\(3\)

\(2\)

\(6\)

\(0\)

\(2\)

\(4\)

\(6\)

\(0\)

\(1\)

\(3\)

\(2\)

\(0\)

\(1\)

\(3\)

\(2\)

\(4\)

\(5\)

\(6\)

\(0\)

\(S_0\)

\(0\)

\(n=7, \ell=3\)

\(\mathbb{Z}_n\)

\(1\)

\(4\)

\(5\)

\(0\)

\(3\)

\(2\)

\(6\)

\(0\)

\(1\)

\(3\)

\(2\)

\(4\)

\(5\)

\(6\)

\(0\)

\(B=\{3,4\}\)

\(B\)

\(S_3\)

\(S_4\)

Find a small \(\ell\)-covering \(B\subseteq \mathbb{Z}_n\)

\(n=7, \ell=3\)

\(\mathbb{Z}_n\)

\(1\)

\(4\)

\(5\)

\(0\)

\(3\)

\(2\)

\(6\)

\(0\)

\(1\)

\(3\)

\(2\)

\(4\)

\(5\)

\(6\)

\(0\)

\(f(n,\ell)\) is the size of the smallest \(\ell\)-covering of \(\mathbb{Z}_n\).

\(f(7,3)\leq |B| = 2\)

\left\lceil \frac{n-1}{\ell} \right\rceil \leq f(n,\ell) \leq n-1

\( 2 = \left\lceil \frac{7-1}{3} \right\rceil \leq \)

\(B=\{3,4\}\)

Find a small \(\ell\)-covering \(B\subseteq \mathbb{Z}_n\)

IP

\begin{aligned} & \min_{x} & & \sum_{i} x_i & \\ & \text{s.t.} & & \sum_{i:j\in S_i} x_i\geq 1 & j\in \Z_n \\ & & & x_i \in \{0,1 \} & i\in \Z_n \\ \end{aligned}

f(n,\ell) = OPT(IP)

Main Questions

Combinatorial: What is the correct bound for \(f(n,\ell)\)?

Algorithmic: How to find a small \(\ell\)-covering?

\(f(n,\ell)=\left\lceil \frac{n-1}{\ell} \right\rceil\)?

No.

\(f(16,5)>3=\lceil \frac{16-1}{5}\rceil\)

Klove et. al. multiple papers in the 2010s: \(f(n,\ell)\) for \(\ell=2,3,4\), and when \(n\) and \(\ell\) are very special

Previous Work

\(f(n,\ell) = O(\frac{n}{\ell}\log n\log \log n)\)

if \(\ell\) is neither too small nor too large

n^{\Omega(\frac{1}{\log \log n})} \leq \ell \leq n^{1-\Omega(\frac{1}{\log \log n})}

Koiliaris & Xu 2019, construction time \(O(n\ell)\)

Chen et. al. 2013: \(f(n,\ell) \leq \frac{n^{1+o(1)}}{\sqrt{\ell}}\), similar construction time

Our results

\(f(n,\ell) = O(\frac{n}{\ell}\log n)\)

A \(f(n,\ell)\log n\) size \(\ell\)-covering can be found in time

\(\tilde{O}(\frac{n}{\ell}) + n^{o(1)}\)

There exist examples where

\(f(n,\ell)=\Omega(\frac{n}{\ell}\frac{\log n}{\log \log n})\)

Our results

\(f(n,\ell) = O(\frac{n}{\ell}\log n)\)

There exist examples where

\(f(n,\ell)=\Omega(\frac{n}{\ell}\frac{\log n}{\log \log n})\)

A \(f(n,\ell)\log n\) size \(\ell\)-covering can be found in time

\(\tilde{O}(\frac{n}{\ell}) + n^{o(1)}\)

\(f(n,\ell) = O(\frac{n}{\ell}\log n)\)

* \(\ell\) is not too small and not too large.

A more refined analysis of \(\varphi(n,\ell)\).

A more refined analysis of covering.

\displaystyle\varphi(n,\ell)=\sum_{\substack{ x\leq\ell \\ \gcd(x,n)=1}}1

\varphi(n)=\varphi(n,n)

Semigroup \((S,\diamond)\), \(A,B\subseteq S\). \(A\diamond B = \{a\diamond b | a\in A, b\in B\}\). \(B\) is an \(A\)-covering, if \(A\diamond B = S\).

Theorem Bollobas et. al. 2009

Let \(G\) be a group, for any \(A\subseteq G\), there is an \(A\)-covering of size \(\frac{|G|}{|A|}(\log |A|+1)\).

\((\Z_{2n},\cdot)\), \(A=\{2,4,6,\ldots,2n\}\). No \(A\)-covering exists.

A more general covering

Our problem \(S=\Z_n\), \(\diamond = \cdot\), \(A = [\ell]\)

Set cover

Given \(\mathcal{S} \subseteq 2^U\).

A collection of sets in \(\mathcal{S}\) covers \(U\) is a set cover.

Formally, if \(\mathcal{S}'\subseteq \mathcal{S}\) such that \(U= \bigcup_{X\in \mathcal{S}'} X\), then \(\mathcal{S}'\) is a set cover of \(U\).

\(\ell\)-covering as set cover

\(U=\Z_n\)

\(S_i=\{ij\pmod{n}|j\leq\ell\}\)

\(\mathcal{S}=\{S_i|i\in\Z_n\}\)

An algebraic special case

Each elements covered by \(b\) sets

\(O\left(\frac{|\mathcal{S}|}{b}\log \ell\right)\) size set cover

(naively) apply to \(\ell\)-covering?

\begin{aligned} &\Z_{n,d}&&=&&\{x|\gcd(x,n)=d,x\in\Z_n\} \\ &\Z_n^*&&=&&\Z_{n,1} \end{aligned}

\(p\) a large prime, \( n=2p, \ell=p-1\). \(p\) only covered by \(S_p\).

No

Idea: Reduce to group case

\begin{aligned} &\Z_{n,d}&&=&&\{x|\gcd(x,n)=d,x\in\Z_n\} \\ &\Z_n^*&&=&&\Z_{n,1} \end{aligned}

\((\Z^*_n,\cdot)\) forms a group. Find \(([\ell]\cap \Z^*_n)\)-covering of \(\Z^*_n\).

\(f^*(n,\ell)\) the smallest \(\ell\)-covering of \(\Z^*_n\) such that all segments has slope in \(\Z^*_n\).

\varphi(n,\ell) = |[\ell] \cap \Z^*_n|

\varphi(n,\ell) = \Omega(\frac{\ell}{n} \varphi(n)) \text{ if } \ell > n^{\Omega(\frac{1}{\log \log n})}

\varphi(n) = |\Z^*_n|

f^*(n,\ell) = O\left(\frac{n}{\ell}\log \ell\right)

When \(\ell = n^{\Omega(\frac{1}{\log \log n})}\)

Previous bound for \(\varphi(n,\ell)\)

\varphi(n,\ell) = \begin{cases} \Omega(\frac{\ell}{n} \varphi(n))& \text{ if } \ell > n^{\Omega(\frac{1}{\log \log n})}\\ \Omega(\frac{\ell}{\log \ell}) & \text{ if } \ell > c \log n\\ \end{cases}

Constant \(c \geq 1\)

\varphi(n,\ell) = \begin{cases} \Omega(\frac{\ell}{n} \varphi(n))& \text{ if } \ell > n^{\Omega(\frac{1}{\log \log n})}\\ \Omega(\frac{\ell}{\log \ell}) & \text{ if } \ell > c \log n\\ \end{cases}

c \log^5 n

Previous bound for \(\varphi(n,\ell)\)

Case 1: \(\ell > c \log^5 n\)

Sieve Theory

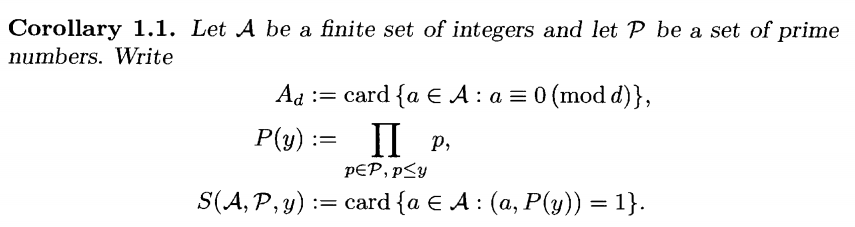
\(\pi(\ell)\geq c_1\frac{\ell}{\log \ell}\) (Prime Number Theorem)

\(\omega(n)\leq c_2\frac{\log n}{\log \log n}\).

\(\omega(n)\leq \frac{\pi(\ell)}{2} \) if \(\ell \geq c\log n\) for sufficiently large \(n\).

Case 2: \(\ell > c \log n\)

\varphi(n,\ell)\geq \pi(\ell)-\omega(n)

\(\pi(n)\): number of primes no larger than \(n\)

\(\omega(n)\): number of distinct prime factors of \(n\)

\varphi(n,\ell)=\Omega\left(\frac{\ell}{\log \ell}\right)

Bound for \(f^*(n,\ell)\)

f^*(n,\ell) = O\left(\frac{n}{\ell}\log n\right)

Using the fact about \(\varphi(n,\ell)\).

When \(\ell = n^{\Omega(\frac{1}{\log \log n})}\)

Case 1: \(\ell > c \log^5 n\)

\begin{aligned} f^*(n,\ell) &= O\left(\frac{\varphi(n)\log \ell}{\frac{\ell}{n}\varphi(n)}\right)\\ &= O\left(\frac{n}{\ell}\log n\right) \end{aligned}

\text{each element covered by } b \text{ sets} \Rightarrow O(\frac{|S|\log \ell}{b})

\varphi(n,\ell) = \Omega(\frac{\ell}{n}\varphi(n))

\begin{aligned} f^*(n,\ell) &= O\left(\frac{\varphi(n)\log \ell}{\frac{\ell}{\log \ell}}\right)\\ &= O\left(\frac{\varphi(n)}{\ell}(\log \ell)^2\right) \\ &= O\left(\frac{n}{\ell}(\log \log n)^2\right)\\ &= O\left(\frac{n}{\ell}\log n\right) \end{aligned}

Case 2: \(c\log n<\ell < c \log^5 n\)

O(\frac{|S|\log \ell}{b})

\varphi(n,\ell) = \Omega(\frac{\ell}{\log \ell})

\ell = O(\log^5 n)

\begin{aligned} f^*(n,\ell)&\leq \varphi(n) \\ &= O\left(\varphi(n)\frac{\log n}{\ell}\right) \\ &= O\left(\frac{n}{\ell}\log n\right) \end{aligned}

Case 3: \(\ell < c \log n\)

We can cover \(\mathbb{Z}_{n,d}\) with \(f^*(\frac{n}{d},\ell) \) segments in \(\mathbb{Z}_{n,d}\).

We can cover \(\mathbb{Z}_n^*\) with \(f^*(n, \ell)\) segments in \(\mathbb{Z}_n^*\).

\(\mathbb{Z}_n\)

We can cover \(\mathbb{Z}_{n,d}\) with \(f^*(\frac{n}{d},\ell) \) segments in \(\mathbb{Z}_{n,d}\).

\(\mathbb{Z}_n\)

\(d \mid x\)

We can cover \(\mathbb{Z}_n^*\) with \(f^*(n, \ell)\) segments in \(\mathbb{Z}_n^*\).

We can cover \(\mathbb{Z}_{n,d}\) with \(f^*(\frac{n}{d},\ell) \) segments in \(\mathbb{Z}_{n,d}\).

\(\mathbb{Z}_n\)

\(d \mid x\)

\(\mathbb{Z}_{n,d}\)

We can cover \(\mathbb{Z}_n^*\) with \(f^*(n, \ell)\) segments in \(\mathbb{Z}_n^*\).

We can cover \(\mathbb{Z}_{n,d}\) with \(f^*(\frac{n}{d},\ell) \) segments in \(\mathbb{Z}_{n,d}\).

\(\mathbb{Z}_n\)

\(d \mid x\)

\(\mathbb{Z}_{n,d}\)

\(\mathbb{Z}^{*}_{\frac{n}{d}}\)

We can cover \(\mathbb{Z}_n^*\) with \(f^*(n, \ell)\) segments in \(\mathbb{Z}_n^*\).

Cover of \(\Z^*_\frac{n}{d}\) using \(\Z^*_{\frac{n}{d}}\) lifts to a cover of \(\Z_{n,d}\) using \(\Z_{n,d}\)

\mathbb{Z}^*_{12}

\mathbb{Z}_{12,2}

\mathbb{Z}_{12,3}

\mathbb{Z}_{12,4}

\mathbb{Z}_{12,6}

\mathbb{Z}_{12,12}

f^*(12,4)

\ell=4

\mathbb{Z}^*_{12}

\mathbb{Z}_{12,2}

\mathbb{Z}_{12,3}

\mathbb{Z}_{12,4}

\mathbb{Z}_{12,6}

\mathbb{Z}_{12,12}

f^*(12,4)

f^*(6,4)

\ell=4

\mathbb{Z}^*_{12}

\mathbb{Z}_{12,2}

\mathbb{Z}_{12,3}

\mathbb{Z}_{12,4}

\mathbb{Z}_{12,6}

\mathbb{Z}_{12,12}

f^*(12,4)

f^*(6,4)

f^*(3,4)

f^*(4,4)

f^*(2,4)

f^*(1,4)

f(12,4)

\leq

\ell=4

\displaystyle f(n,\ell) \leq \sum_{d|n} f^*(\frac{n}{d},\ell)

\begin{aligned} &\leq \sum_{d|n}O\left(\frac{n}{d}\frac{\log n}{\ell} \right)+1\\ &\leq O\left(\sigma(n)\frac{\log n}{\ell}\right) + d(n)\\ \end{aligned}

When \(\ell = n^{\Omega(\frac{1}{\log \log n})}\)

O\left(\frac{n}{\ell}\log n\log \log n\right) + n^{O\left(\frac{1}{\log \log n}\right)}

\leq

\displaystyle f(n,\ell) \leq \sum_{d|n} f^*(\frac{n}{d},\ell)

When \(\ell = n^{\Omega(\frac{1}{\log \log n})}\)

O\left(\frac{n}{\ell}\log n\log \log n\right) + n^{O\left(\frac{1}{\log \log n}\right)}

\sigma(n) = O(n \log \log n)

d(n)

Dominates when \(n\) is large

Improvements

Using \(\Z^*_n\) to cover \(\Z_{n,d}\) for many \(d\)

A better estimate for \(\varphi(n,\ell)\) using sieve theory

\varphi(n,\ell) = \begin{cases} \Omega(\frac{\ell}{n} \varphi(n))& \text{ if } \ell > c \log^5 n\\ \Omega(\frac{\ell}{\log \log n}) & \text{ if } \ell > c \log n\\ & \text{ and } \ell \leq c \log^5 n\\ \end{cases}

\mathbb{Z}^*_{12}

\mathbb{Z}_{12,2}

\mathbb{Z}_{12,3}

\mathbb{Z}_{12,4}

\mathbb{Z}_{12,6}

\mathbb{Z}_{12,12}

Larger Cover

\(\ell = 4\)

\(g(n,\ell)\) the smallest \(\ell\)-covering of \(\bigcup_{d|n,d\leq \ell'} \Z_{n,d}\) such that all segments has slope in \(\Z^*_n\).

\ell' := \frac{\ell}{c \log^5 n}

g(n,\ell) = O(f^*(n,\ell))

\displaystyle f(n,\ell) \leq \sum_{d\in B} g\left(\frac{n}{d},\ell\right)

\(\mathbb{D}_n\) be the set of divisors of \(n\).

\((\mathbb{D}_n,\odot)\), where \(a\odot b = \gcd(ab,n)\).

Let \(A = \{i \mid i\in \mathbb{D}_n, i\leq \ell'\}\).

Find a \(A\)-covering \(B\) so the sum is small.

If \(B\) is an \(A\)-covering of \(\mathbb{D}_n\), then

\(B = \{1\}\cup (\mathbb{D}_n\setminus A)\)

\displaystyle f(n,\ell) \leq \sum_{d\in B} g\left(\frac{n}{d},\ell\right)

\begin{aligned} &\leq \sum_{d\in B}O\left(\frac{n}{d}\frac{\log n}{\ell} \right)+1\\ &\leq O(\frac{n}{\ell}\log n) + |B|\\ &\leq O(\frac{n}{\ell}\log n) + n^{O(\frac{1}{\log \log n})}\\ \end{aligned}

\begin{aligned} \leq O(\frac{n}{\ell}\log n) \end{aligned}

# of divisors

larger than \(\ell'\)

\(\ell\) is small: \(\ell=n^{1-\Omega(\frac{1}{\log \log n})}\)

\(B = \mathbb{D}_m\) for some \(m|n\) and \(m\geq \frac{n}{\ell'}\)

\(\sigma(m) = O(m)\)

\displaystyle f(n,\ell) \leq \sum_{d\in B} g\left(\frac{n}{d},\ell\right)

\begin{aligned} &\leq \sum_{d|m}O\left(\frac{n}{d}\frac{\log n}{\ell} \right)+1\\ &\leq O\left(\frac{n}{m}\sigma(m)\frac{\log n}{\ell}\right) + d(m)\\ \end{aligned}

\begin{aligned} &\leq O\left(\frac{n}{\ell}\log n\right) + \left(\frac{n}{\ell'}\right)^{\frac{c}{\log \log n}}\\ &\leq O\left(\frac{n}{\ell}\log n\right)\\ \end{aligned}

\(B = \mathbb{D}_m\) for some \(m|n\) and \(m\geq \frac{n}{\ell'}\)

Theorem

There exists a \(m|n\) such that \(m = n^{\Omega(\frac{1}{\log \log \log n})}\) and \(\sigma(m)=O(m)\).

Such \(B\) exists when \(\ell\) is large: \(\ell = n^{1-O(\frac{1}{\log \log \log n})}\)

f(n,\ell) = O\left(\frac{n}{\ell}\log n\right)

\(\sigma(m) = O(m)\)

and

Future Work

Conjecture: \(f(n,\ell) = O(\frac{n}{\ell}\log \ell)\) if \(\ell = \Omega(\log n)\)

What about \(\ell\)-covering of arbitrary set \(X\subseteq \Z_n\)?

Other interesting semigroups, e.g. \(\Z_n\times \Z_m\).

\varphi(n,\ell) = \Omega(\frac{\ell}{n} \varphi(n)) \text{ if } \ell > c \log n

Conjecture:

Thank you

Limited-magnitude errors:

Jiang A., Langberg M., Schwartz M., Bruck J.: Trajectory codes for flash memory. IEEE Trans. Inf. Theory 59(7), 4530–4541 (2013).

Sieve theory:

Alina Carmen Cojocaru, M Ram Murty, et al. An introduction to sieve methods and their applications, volume 66. Cambridge University Press, 2006.

References

\displaystyle f(n,\ell) \leq \sum_{d|m} f^*(\frac{n}{d},\ell)

\displaystyle n = \prod_{i=1}^k p_i

\displaystyle m = \prod_{i=1}^j p_i \geq \frac{n}{\ell'}

If \(d|n\), then \(d=d_1d_2\), where \(d_1|m\), and \(d_2\leq \ell'\).

How large is \(d(m)\)?

\begin{aligned} &\leq \sum_{d|m}O\left(\frac{n}{d}\frac{\log n}{\ell} \right)+1\\ &\leq O\left(\sigma(n)\frac{\log n}{\ell}\right) + d(m) \end{aligned}

d(n) = n^{O(\frac{1}{\log \log n})}

d(m)

\leq 2d(m')

=m'^{O(\frac{1}{\log \log m'})}

= \left(\frac{n}{\ell}\log^u \frac{n}{\ell}\right)^{O\left(\frac{1}{\log \log \frac{n}{\ell}}\right)}

= \frac{n}{\ell} c\log^5 \frac{n}{\ell}

< \frac{n}{\ell'}

m':=\frac{m}{p_j}

\begin{aligned} f(n,\ell) &\leq \sum_{d|m} f^*(\frac{n}{d},\ell)\\ &\leq \sum_{d|m}O\left(\frac{n}{d}\frac{\log n}{\ell} \right)+1\\ &\leq O\left(\sigma(n)\frac{\log n}{\ell}\right) + d(m)\\ &= \underbrace{ O\left(\frac{n}{\ell}\log n\log \log n\right)}_{\textbf{main term}} + {\color{red} \underbrace{\left(\frac{n}{\ell}\log^u \frac{n}{\ell}\right)^{O\left(\frac{1}{\log \log \frac{n}{\ell}}\right)}}_{\textbf{error term}}}\\ &= O\left(\frac{n}{\ell}\log n\log \log n\right) \end{aligned}

\(f(n,\ell) = O(\frac{n}{\ell}\log n\log \log n)\)

\(f(n,\ell) = O(\frac{n}{\ell}\log n)\)

Better choice of \(m\)

Alternative choice of divisor cover

A \(O(f(n,\ell)\log n)\) size \(\ell\)-covering can be found in time

\(\tilde{O}(\frac{n}{\ell}) + n^{o(1)}\)

Symmetric LP

Randomized rounding

Sampling

IP

\begin{aligned} & \min_{x} & & \sum_{i} x_i & \\ & \text{s.t.} & & \sum_{i:j\in S_i} x_i\geq 1 & j\in \Z_n \\ & & & x_i \in \{0,1 \} & i\in \Z_n \\ \end{aligned}

LP Relaxation

\begin{aligned} & \min_{x} & & \sum_{i} x_i & \\ & \text{s.t.} & & \sum_{i:j\in S_i} x_i\geq 1 & j\in \Z_n \\ & & & 0 \leq x_i \leq 1 & i\in \Z_n \\ \end{aligned}

Input size: \(O(n^2)\). \(n\) variables and \(n\) constraints.

Symmetric LP

Certain permutation of variables does not change the LP.

\begin{bmatrix} x_1 \\ x_2 \\.\\.\\.\\x_n \end{bmatrix} \xRightarrow[\textbf{permutation group G}]{\forall \textbf{permutation } \pi \text{ in}} \begin{bmatrix} x_{\pi(1)} \\ x_{\pi(2)} \\.\\.\\.\\x_{\pi(n)} \end{bmatrix}

\(\textbf{fesible}\) \(\xRightarrow[\textbf{ }]{}\) \({}\textbf{fesible}\)

\(\textbf{c}\cdot\textbf{x}\) \(\xRightarrow[\textbf{ }]{\textbf{same value}}\) \(\textbf{c}\cdot\pi\textbf{ x}\)

\(G\)-symmetric LP

Symmetric LP

Example:

\(S_n\)-symmetric LP

\begin{aligned} & \min_{x} & & \sum_{i=1}^n x_i & \\ & \text{s.t.} & & \sum_{i=1}^n x_i\geq n \end{aligned}

Symmetric LP

\(G\)-symmetric LP has a \(G\)-symmetric optimum.

c\cdot x^* = c\cdot \pi x^*

\begin{aligned} & \min_{x} & & \sum_{i=1}^n x_i & \\ & \text{s.t.} & & \sum_{i=1}^n x_i\geq n \end{aligned}

x = (n,0,0,\ldots,0)

Optimum

\(G\)-symmetric optimum

x = (1,1,1,\ldots,1)

x_i = x_j ~ \forall i,j

Let \(G\) be a permutation group that consists of all permutations that swaps \(i\) and \(j\) if \(\gcd(i,n)=\gcd(j,n)\). LP is \(G\)-symmetric.

Reduce variables

\begin{aligned} & \min_{x} & & \sum_{i} x_i & \\ & \text{s.t.} & & \sum_{i:j\in S_i} x_i\geq 1 & j\in \Z_n \\ & & & 0 \leq x_i \leq 1 & i\in \Z_n \\ \end{aligned}

\begin{aligned} & & & x_i = x_j & \text{ if }\gcd(i,n)=\gcd(j,n) \\ \end{aligned}

Replace each \(x_i\) with \(y_d\) where \(\gcd(i,n)=d\)

Reduce variables

\begin{aligned} & \min_{y} & & \sum_{i} y_{\gcd(i,n)} & \\ & \text{s.t.} & & \sum_{i:j\in S_i} y_{\gcd(i,n)}\geq 1 & j\in \Z_n \\ & & & 0 \leq y_{\gcd(i,n)} \leq 1 & i\in \Z_n \\ \end{aligned}

Reduce variables

\begin{aligned} & \min_{y} & & \sum_{d:d|n} \varphi(\frac{n}{d}) y_d & \\ & \text{s.t.} & & \sum_{d:d|j} \frac{\varphi(n/c, d \ell / c)\varphi(n/d)}{\varphi(n/c)} y_d\geq 1 & j\in \Z_n \\ & & & 0\leq y_d\leq 1 & d|n \\ \end{aligned}

We have only \(d(n)\) variables.

LP (compact)

\begin{aligned} & \min_{y} & & \sum_{d:d|n} \varphi(\frac{n}{d}) y_d & \\ & \text{s.t.} & & \sum_{d:d|c} \frac{\varphi(n/c, d \ell / c)\varphi(n/d)}{\varphi(n/c)} y_d\geq 1 & c|n \\ & & & 0\leq y_d\leq 1 & d|n \\ \end{aligned}

We have only \(d(n)\) variables and inequalities.

\begin{aligned} & \min_{y} & & \sum_{d:d|n} \color{red}{\varphi(\frac{n}{d}) y_d} & \\ & \text{s.t.} & & \sum_{d:d|c} \frac{\varphi(n/c, d \ell / c)\color{red}{\varphi(n/d)}}{\varphi(n/c)} {\color{red}y_d} \geq 1 & c|n \\ & & & 0\leq y_d & d|n \\ \end{aligned}

LP*

\begin{aligned} & \min_{d} & & \sum_{d:d|n} u_d & \\ & \text{s.t.} & & \sum_{d:d|c} \frac{\varphi(n/c, d \ell / c)}{\varphi(n/c)} u_d\geq 1 & c|n \\ & & & 0\leq u_d\leq \varphi(n/d) & d|n \end{aligned}

Let \(u_d=\varphi(n/d)y_d\), We have the following concise form.

Randomized rounding

\(\underline{\textbf{Cover}(n,\ell)}\)

compute the prime factorization of \(n\)

compute \(\varphi(n/c,d\ell/c)\) and \(\varphi(n/c)\) for all \(d|c|n\)

compute the optimum for \(\mathrm{LP}^*\)

\(C\leftarrow \empty\)

repeat \(4\log{n}\) times

for \(d|n\):

if \(u_d\geq1\):

\(C\leftarrow C\cup (S\sim {\Z_{n,d}\choose \lceil u_d \rceil})\)

else if \(u_d > (x\sim[0,1])\):

\(C\leftarrow C\cup (S\sim {\Z_{n,d}\choose 1})\)

return \(C\)

Sample ~\(\mathbb{E}[u_d]\)

distinct elements

from \(\Z_{n,d}\)

Construct and solve the LP

Sampling \(k\) elements in \(\Z_n^*\)

If \(k<\frac{\varphi(n)}{2}\). Sample a random element \(x\sim \Z_n\), if \(x\in\Z_n^*\) and we hasn't get enough elements, pick it. Repeat at most \(8k \log(n)\) times.

The runing time of the algorithm is \(O(k \mathrm{polylog}(n))\) and by Chernoff bound the success probability \(\geq 1-\frac{1}{n}\).

If \(k\geq \frac{\varphi(n)}{2}\), then find all elements in \(\Z_n^*\) by brute force and pick \(k\) from it.

Theorem: There is an algorithm which successfully returns \(X\sim {\Z^*_n \choose k}\) in \(\tilde{O}(k)\) time with probability at least \(1-\frac{1}{n}\).

Sampling \(k\) elements in \(\Z_n^*\)

Randomized rounding

\(\underline{\textbf{Cover}(n,\ell)}\)

compute the prime factorization of \(n\)

compute \(\varphi(n/c,d\ell/c)\) and \(\varphi(n/c)\) for all \(d|c|n\)

compute the optimum for \(\mathrm{LP}*\)

\(C\leftarrow \empty\)

repeat \(4\log{n}\) times

for \(d|n\):

if \(u_d\geq1\):

\(C\leftarrow C\cup (S\sim {\Z_{n,d}\choose \lceil u_d \rceil})\)

else if \(u_d > (x\sim[0,1])\):

\(C\leftarrow C\cup (S\sim {\Z_{n,d}\choose 1})\)

return \(C\)

\(\tilde{O}(u_d) \)

\(n^{o(1)}\)

\(\tilde{O}(\sum_{d} u_d) = \tilde{O}(f(n,\ell))\)

Theorem:

The algorithm takes \(\tilde{O}(f(n,\ell)) + n^{o(1)}\) time and computes an expected size \(f(n,\ell)\log n\) \(\ell\)-covering set with constant probability.