计算机科学与技术在WEB3暨区块链的
应用与发展
长庚大学 郑振牟
自我介绍
- 2007: PhD, Harvard University
- 2007: 台湾大学助理教授
- 2011: Humboldt Fellow, TU Darmstadt
- 2013: 九州大学外国人特別研究員
- 2016: 大阪大学特任准教授
- 2020: 金沢大学准教授
- 2022: Chief Cryptographer, NASDAQ: BTQ
- 2023: 长庚大学教授
计算机科学所学何事?
- Abstraction 抽象化:指缩减一个概念或是一个现象的资讯含量来将其广义化的过程,此时只保存特定的资讯
- Set 集合
- Function 函數
- Turing machine 图灵机
- Algorithm 算法
- ...
- 『如果它看起来像鸭子,游起来像鸭子,叫起来也像鸭子,那它很可能就是一只鸭子。』
货币的抽象化
- 交换媒介
- 记账单位
- 价值储藏
- 延期支付标准
Rai stone from Yap

现代加密货币的起源:
Bitcoin 比特币
- A cryptocurrency invented by Satoshi Nakamoto
- Verified transactions are recorded in a public distributed ledger (分散式帐本)
- A decentralized (去中心化) digital currency
关键支撑技术
- Ownership established using digital signature (数字签名)
- Transaction history in tamper-evident logs, a.k.a. blockchain (区块链)
- Decentralization via consensus protocol (共识协议)
数字签名
插话: 堆叠炮弹问题

丢番图方法
- \(1^2+2^2+\cdots+x^2=\frac{x(x+1)(2x+1)}{6}=y^2\)
- Two trivial solutions: \((x,y)=(0,0)\) or \((1,1)\)
- The line through these two points is \(y=x\), which intersects with the curve and gives the equation \[x^3-\frac{3}{2}x^2+\frac{1}{2}x=0\]
- The third root is \(x=\frac{1}{2}\)
Repeat for (1,1) & (1/2,-1/2)
- The line is \(y=3x−2\), so the equation is \[x^3-\frac{51}{2}x^2+\cdots=0\]
- The third root is \(x=24\), so \(y=70\), i.e., \[1^2+2^2+\cdots+24^2=70^2\]
- If we keep repeating this procedure, we'll obtain infinitely many rational solutions to our equation
- However, it can be shown that \((24,70)\) is the only non-trivial solution in positive integers
同余数问题
- The question of which integers \(n\) can occur as areas of right triangles with rational sides is known as the congruent number problem
- E.g., \(n=5\): are there rational numbers \(a,b,c\) s.t. \[a^2+b^2=c^2,ab=10?\]
- Equivalently, \(c^2+20=(a+b)^2,c^2-20=(a-b)^2\)
- Let \(x=(c/2)^2\): \(y^2=(x+5)x(x-5)=x^3-25x\)
丢番图方法
- Consider the tangent line at \((−4,6)\): \(y=\frac{23}{12}x+\frac{41}{3},\) which intersects the curve and gives \[x^3-\left(\frac{23}{12}\right)^2x^2+\cdots=0\]
- The third root is \((23/12)^2+4+4=(41/12)^2\), i.e., \[a=\frac{20}{3},b=\frac{3}{2},c=\frac{41}{6}\]
- There are infinitely many other solutions, which can be obtained by successively repeating this procedure
An elliptic curve \(E\) is the graph of an equation of the form \(y^2=x^3+Ax+B\), where \(A\) and \(B\) are constants. This will be referred to as the Weierstraß equation for an elliptic curve. We will need to specify what set \(A,B,x\) and \(y\) belong to. Usually, they will be taken to be elements of a field, for example, the real numbers \(\mathbb R\), the complex numbers \(\mathbb C\), the rational numbers \(\mathbb Q\), one of the finite fields \(\mathbb F_p(=\mathbb Z/p\mathbb Z)\) for a prime \(p\), or one of the finite fields \(\mathbb F_q\), where \(q=p^k\) with \(k\geq 1\). If \(K\) is a field with \(A,B\in K\), then we say that \(E\) is defined over \(K\).
椭圆曲线
椭圆曲线点群
- If we want to consider points with coordinates in some field \(L\supseteq K\), we write \(E(L)\)
- By definition, this always contains the point at infinity: \[E(L)=\Big\{\infty\Big\}\bigcup\Big\{(x,y)\in L\times L:y^2=x^3+Ax+B\Big\}\]
- \(E(L)\) is an abelian group (阿贝尔群)
\(E(L)\) 群运算

椭圆曲线密码学
- Security depends on the hardness of the elliptic curve discrete logarithm problem (ECDLP, 离散对数问题)
- Given a point \(Q\in G\subseteq E(L)\) and a generator \(P\) of \(G,\) find an integer \(n\) s.t. \(nP=Q\)
- Pros: smaller keys and ciphertexts for achieving same security level as DLP-based cryptosystems
- \(\text{160--256}\) bits vs. \(\text{1024--3072}\) bits
- Cons: security is achieved only over secure curves
ECDSA
- To sign a message \(m\):
- \(h\leftarrow H(m)\)
- \(k\stackrel{\$}{\leftarrow}(\mathbb Z/q\mathbb Z)^*\)
- \(\color{blue}r\color{black}\leftarrow f(kP)\bmod q\)
- \(\color{blue}s\color{black}\leftarrow(h+\color{red}x\color{blue}r\color{black})/k\bmod q\)
- To verify signature \(\color{blue}(r,s)\):
- \(h\leftarrow H(m)\)
- \(a\leftarrow h/\color{blue}s\color{black}\bmod q\)
- \(b\leftarrow \color{blue}r\color{black}/\color{blue}s\color{black}\bmod q\)
- \(f(aP+bQ)\stackrel{?}{=}\color{blue}r\color{black}\bmod q\)
Why it works? \[f(aP+bQ)=f(aP+b\color{red}x\color{black}P)=f(\frac{h+\color{red}x\color{blue}r\color{black}}{s}P)=f(kP)\]
比特币的数字签名
- ECDSA over curve secp256k1
- Public/private keys: 33 or 65 bytes
- Signatures: 71, 72, or 73 bytes
- Bitcoin address = RIPEND160(SHA256(pk)): 20 bytes
- Often in Base58Check encoding
比特币交易帐本
- Transaction consists of \(\geq 1\) inputs and \(\geq 1\) outputs
- To prevent double spending, each input must refer to a previous unspent transaction output (UTXO)
- Except for coin generation, e.g.: genesis block
- How to ensure integrity of transaction ledger?
Hash function 杂凑函数
-
One-way function 单向函数
- A function \(f\) that is easy to compute on every input \(x\), but hard to invert given the image \(f(x_0)\) of a random input \(x_0\)
- Ideal model: random oracle 随机预言机
- In practice: cryptographic hash function
- SHA-256, SHA-512
- SHA3 (Keccak)
Merkel tree
防篡改日志: 区块链
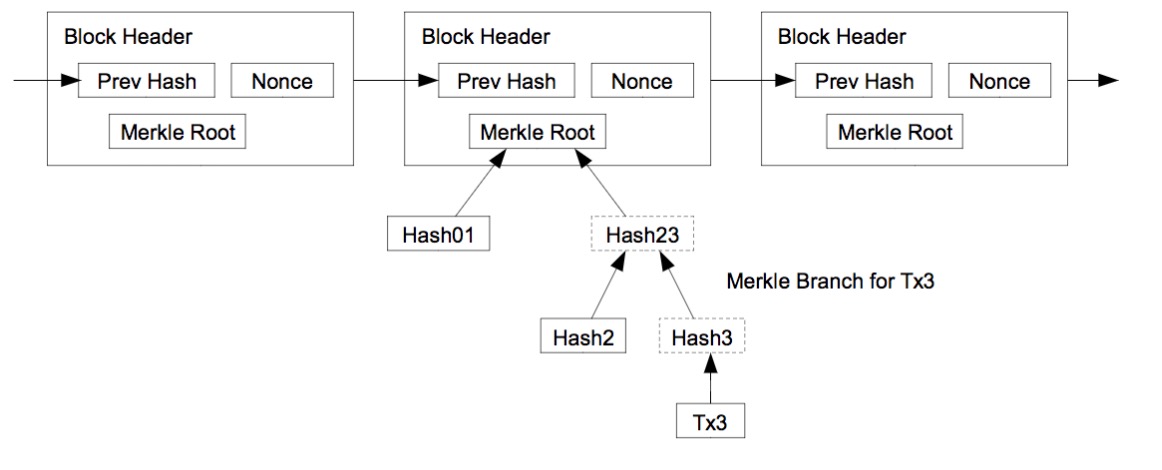
比特币共识协议
- New transactions are broadcast to all nodes
- Each node collects transactions into a block and broadcasts the block as its proof of work (PoW)
- Other nodes accept the block only if all transactions in it are valid, i.e., unspent with valid signatures
- Nodes express their acceptance of the block by including its hash in the next block they create
比特币挖矿激励机制
- Bitcoin miners' incentives
- Transaction fees
- Block rewards
- Started being 50 bitcoins in 2009, now 3.125
- Cut in half every 4 years to limit supply to ≈21M
- Best strategy: when there are multiple chains of blocks, follow the longest chain of blocks
| opcode | mnemonic | description |
|---|---|---|
| 0x01–0x4b | push next opcode bytes of data | |
| 0x69 | OP_VERIFY | if (pop() != true) then fail |
| 0x76 | OP_DUP | let x := pop() in push(x) push(x) |
| 0x87 | OP_EQUAL | push(pop() == pop()) |
| 0x88 | OP_EQUALVERIFY | = OP_EQUAL OP_VERIFY |
| 0xa9 | OP_HASH160 | push(RIPEND160(SHA256(pop()))) |
| 0xac | OP_CHECKSIG | verify signature |
Executing P2PKH scripts

- Pay-to-PubkeyHash
- scriptSig: <sig> <pubKey>
- scriptPubKey: OP_DUP OP_HASH160 <pubKeyHash?> OP_EQUALVERIFY OP_CHECKSIG
- Pay-to-ScriptHash
- scriptSig: ...signatures... <serialized script>
- scriptPubKey: OP_HASH160 <scriptHash> OP_EQUAL
Ethereum 以太坊
- Proposed in late 2013 by Vitalik Buterin
- Went live on 30 July 2015
- Stewarded by nonprofit foundation
- Turing-complete scripts, a.k.a. smart contracts (智能合约)
- A contract is a program that lives on the blockchain
- A dApp is a collection of integrated contracts
- A decentralized autonomous organization (DAO) is an organization represented by rules encoded as contracts on a blockchain
智能合约范例
contract NameRegistry {
mapping(bytes32 => address) public registryTable;
function claimName(bytes32 name) {
if (msg.value < 10) {
throw;
}
if (registryTable[name] == 0) {
registryTable[name] = msg.sender;
}
}
}Web3 区块链应用
- Electronic payment
- Asset tokenization
- Provenance tracking
- Digital identity
- Custody & escrow
- Automation
- Non-fugible token (NFT)
Web3 区块链挑战
- Operating models and regulation
- Scalability
- Privacy
- Latency
- Integration
隐私保护?
- \(H(x)\) is a "proof" of \(x\)
- To verify, however, need to reveal \(x\)
- Zero-knowledge proofs (零知识证明)
- Can prove without revealing \(x\)
超越数字签名
- Standard digital signature on message \( x \):
- "I swear that the signer said \( x \)."
- Beyond digital signature:
- "The signer said \( \color{red}x\color{black} \), which I'm not going to disclose here, but I swear that \( f(\color{red}x\color{black})=y \)."
应用范例
- CA signs Cert: "Batman was born on Jan 1, 1976"
- \( f(x,\color{red}w\color{black})=1 \) if and only if:
- \( \color{red}w\color{black} \) is a valid certificate signed by CA
- \( \color{red}w\color{black} \) says as of today, \( x \) is over 18 years old
- Beers for Batman if \( f(\text{Batman},\color{red}\text{Cert}\color{black})=1 \)
Commitment 承诺方案
(互联网上猜拳)
- Cryptographic commitment 承诺方案
- Commit: \( c=\text{commit}(r,m) \)
- Verify: \( \text{verify}\Big(r,m,c\Big)? \)
- Security properties
- Hiding: difficult to find \( m \) given \( c=\text{commit}\left(r,m\right) \)
- Binding: difficult to find \( r',m'\neq m \) s.t. \( \text{verify}\Big(r',m',\text{commit}(r,m)\Big) \)
Proving \( x\in X \) via Merkle tree
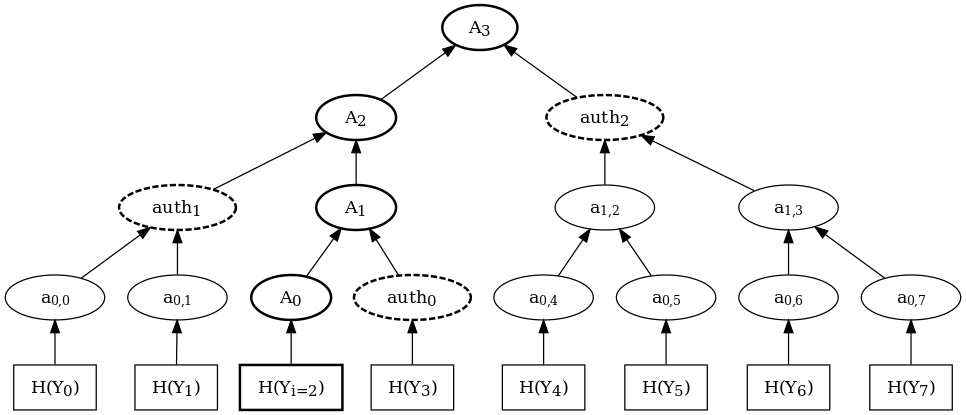
Proving \( f(x)=y \)
- Syntax of (polynomial) functional commitment
- \( c=\text{commit}(r,f) \)
- \( (y,\pi)=\text{eval}(r,f,x) \)
- \( \text{verify}\Big(c,x,y,\pi\Big) \) iff \( \exists r\text{ s.t. }c=\text{commit}(r,f) \) and \( f(x)=y \)
- Example (Merkle tree)
- Leaves \( y_0,y_1,\ldots,y_{n-1} \) define \( f:\Big\{0,1,\ldots,n-1\Big\}\rightarrow Y \)
- Authentication path encodes (binary expansion of) \( i\in\Big\{0,1,\ldots,n-1\Big\} \) and thus proves \( f(i)=y_i \)
Why polynomials?
- \( f_{v+w}=f_v+f_w, f_{v\odot w}=f_vf_w \) for coordinate-wise product \( \odot \) \[ \Big(\because\text{ev}\in k[X]\times k\rightarrow k\cong k[X]\rightarrow k\rightarrow k\Big) \]
- Lemma [Schwartz-Zippel] \[ \text{Pr}_{r\in k}\Big(f(r)=g(r)\Big)\leq\frac{d}{|k|}\text{ for }f\neq g\text{ with }\deg f,\deg g\leq d \]
- Zero test: \( f(\omega)=0\ \forall\omega\in\Omega \)
- Sum check: \( \sum_{\omega\in\Omega}f(\omega)=0 \)
- Product check: \( \prod_{\omega\in\Omega}f(\omega)=1 \)
Interactive (oracle) proof
交互式 (预言机) 证明
- IP allows Prover P to prove Statement S to (computationally bounded) Verifier V via dialogue
- Completeness: If S is true, then V should be convinced with probability 1
- Soundness: If S is false, then V should be convinced with a (very) small probability
- Example (trivial): NP \( \subset \) IP
- IOP: dialogue consists of probabilistically checkable proofs, implemented by e.g. functional commitment
交互式零知识证明
- V learns nothing beyond S is true
- Consider special S: \( y=f(x,\color{red}w\color{black}) \)
- Can simulate the dialogues without knowing \(\color{red}w\color{black}\)
- Example: Blind V with two colored balls
应用范例
- Prover: "I know integers \( \color{red}p\color{black},\color{red}q\color{black} \) s.t. \( n=\color{red}pq\color{black} \)"
- Prover commits to three polynomial functions: \[ \color{red}r_p\color{black}X+\color{red}p\color{black},\color{red}r_q\color{black}X+\color{red}q\color{black},\text{ and }\color{red}r_pr_q\color{black}X^2+(\color{red}r_pq\color{black}+\color{red}pr_q\color{black})X+n \]
- Verifier challenges Prover with random \( r \) and checks whether \( (\color{red}r_p\color{black}r+\color{red}p\color{black})(\color{red}r_q\color{black}r+\color{red}q\color{black})\stackrel{?}{=}\color{red}r_pr_q\color{black}r^2+(\color{red}r_pq\color{black}+\color{red}pr_q\color{black})r+n \)
- Lemma [Schwartz-Zippel] \[ \text{Pr}_{r\in k}\Big(f(r)=g(r)\Big)\leq\frac{d}{|k|}\text{ for }f\neq g\text{ with }\deg f,\deg g\leq d \]
Schnorr 离散对数零知识证明
- S: "I know \( \color{red}x\color{black} \) s.t. \( y=g^{\color{red}x\color{black}} \)"
- P \( \rightarrow \) V: \( r=g^{\color{red}k\color{black}} \)
- P \( \leftarrow \) V: \( e \)
- P \( \rightarrow \) V: \( s=\color{red}k\color{black}-\color{red}x\color{black}e \)
- V checks: \( r\stackrel{?}{=}g^sy^e\left(=g^{\color{red}k\color{black}-\color{red}x\color{black}e}(g^x)^e\right) \)
- Fiat-Shamir heuristic turns (most) IP to NIROP (Non-Interactive Random-Oracle Proof)
- Schnorr's signature: \( \pi=(r,s) \) for \( e=H(r||m) \)
- zk-NARK (Noninteractive ARgument of Knowledge)
知识提取器
How Sony PS3 got hacked in 2011:
\[ \left\{\begin{aligned} s_1 & =\color{red}k\color{black}-\color{red}x\color{black}e_1 \\ s_2 &= \color{red}k\color{black}-\color{red}x\color{black}e_2 \end{aligned}\right. \]
zk-SNARK
- Consider special zk-NARK:
- Proof \( \pi \) proves P knows a \( \color{red}w\color{black} \) s.t. \( y=f(x,\color{red}w\color{black}) \)
- If \( \pi \) is "small" compared with \( f \), e.g., \( |\pi|=O(\log|f|) \), then we say it is succinct, or zk-SNARK
- Questions
- What can we do with a zk-SNARK?
- How to "compress" \( \pi \)?
- How to encode (interesting) \( f \)?
zk-SNARKing C2PA
-
Coalition for Content Provenance and Authenticity
- Camera signs all photos taken: \( s=\text{sign}(p) \)
- Publisher/consumer verifies: \( \text{verify}(p,s)? \)
- What if \( p'=f(p) \) where \( f \) crops, resizes, rotates, ... \( p \)?
- \( \pi \): "I know \( \color{red}p\color{black},\color{red}s\color{black} \) s.t. \( \text{verify}(\color{red}p\color{black},\color{red}s\color{black}) \) & \( p'=f(\color{red}p\color{black}) \)"
- For zk-SNARKs, \( |\pi|\ll |f|=\mathcal O(|p|) \)
以太坊基金會
Semaphore 協議
- "Users who broadcast a signal will not expose their identity"
- "Specifically, an adversary will only know they're a user in the group, but not which user"
- "Users cannot broadcast two different signals on the same topic twice"
实现技术细节
- Identity commitment integrity: \[ \text{id}_\text{comm}=\text{Commit}_{\text{id}_\text{trapdoor}}(\text{id}_\text{pub},\text{id}_\text{nullifier}) \]
- Merkle path validity: \[ (\text{id\textunderscore path},\text{id\textunderscore path\textunderscore index})\text{ is a valid Merkle path from id}_\text{comm}\text{ to root} \]
- Nullifiers hash integrity: \[ \text{nullifiers\textunderscore hash}=\text{PRF}_{\text{id}_\text{nullifier}}(\text{external\textunderscore nullifier},\text{id\textunderscore path\textunderscore index}) \]
- Signal authorization: \[ \text{Verify}(\text{id}_\text{pub},(\text{external\textunderscore nullifier},\text{signal\textunderscore hash}),\text{signature}) \]
RS-encoded IOP
- Think of \( v\in V \) as a function \( H\rightarrow F_q \) for \( |H|=\dim V \)
- Encode \( v \) as \( f_v \) via Lagrange interpolation
- \( f_v(X)=r(X)+q(X)\prod_{h\in H}(X-h) \)
- S.t. \( \forall h\in H,r(h)=v(h) \)
- V can now query \( f_v(x) \) for some \( x\in L \)
- Intuition: ZK if \( H\cap L=\varnothing \) and \( \deg q \) is large enough
- (FRI) low-degree test: Check if \( \deg f_v \) is small enough
- Encode \( y=f(x,\color{red}w\color{black}) \) into R1CS: \( Az\odot Bz=Cz \), where:
- \( A,B,C \) are matrices depending on \( f \)
- \( z=\begin{bmatrix} 1 & u & \color{red}w\color{black} & x & y \end{bmatrix}^T \)
- \( u \) is auxiliary variables
- Lincheck RS-encoded IOP: \( y_A=Az, y_B=Bz, y_C=Cz \)
- Rowcheck RS-encoded IOP: \( y_A\odot y_B=y_C \)
R1CS 范例
\[ y=x^3: \boxed{\begin{aligned} x\cdot x & =u \\ u\cdot x & =y \end{aligned}} \]
\[ 0\leq x<8: \boxed{\begin{aligned} 1\cdot(x_0+2x_1+4x_2) & =x \\ x_0\cdot x_0 & =x_0 \\ x_1\cdot x_1 & =x_1 \\ x_2\cdot x_2 & =x_2 \end{aligned}} \]
\(r=\) if \(b\) then \(t\) else \(f\): \[ \boxed{\begin{aligned} (t-f)\cdot b & =r-f \\ b\cdot b & =b \end{aligned}} \]
DSL (领域专用语言)
范例: Merkle tree

ZoKrates
- Witness contains array of arrays of hash values along authentication path
- Well-known trick to include the indices of these hash values at each level
- Not strictly necessarily but for easy programming
- Will expand to nested if-then-else in R1CS anyway
field mut digest = leaf;
for u32 i in 0..DEPTH {
assert(path[i][indices[i]] == digest);
digest = hash(path[i]);
}
assert(digest == root);\(\text{\tt fold}\) in Keelung
\(\text{\tt foldl :: Foldable t => (b -> a -> b) -> b -> t a -> b}\)
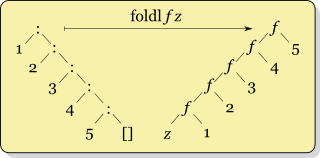
merkleProof :: Int -> Number -> Comp ()
merkleProof depth root = do
leaf <- inputNum
path <- inputs2 depth 2
digest <- foldlM (\digest p -> do
assert (digest `existsIn` p)
hash p)
leaf
path
assert (digest `Eq` root)