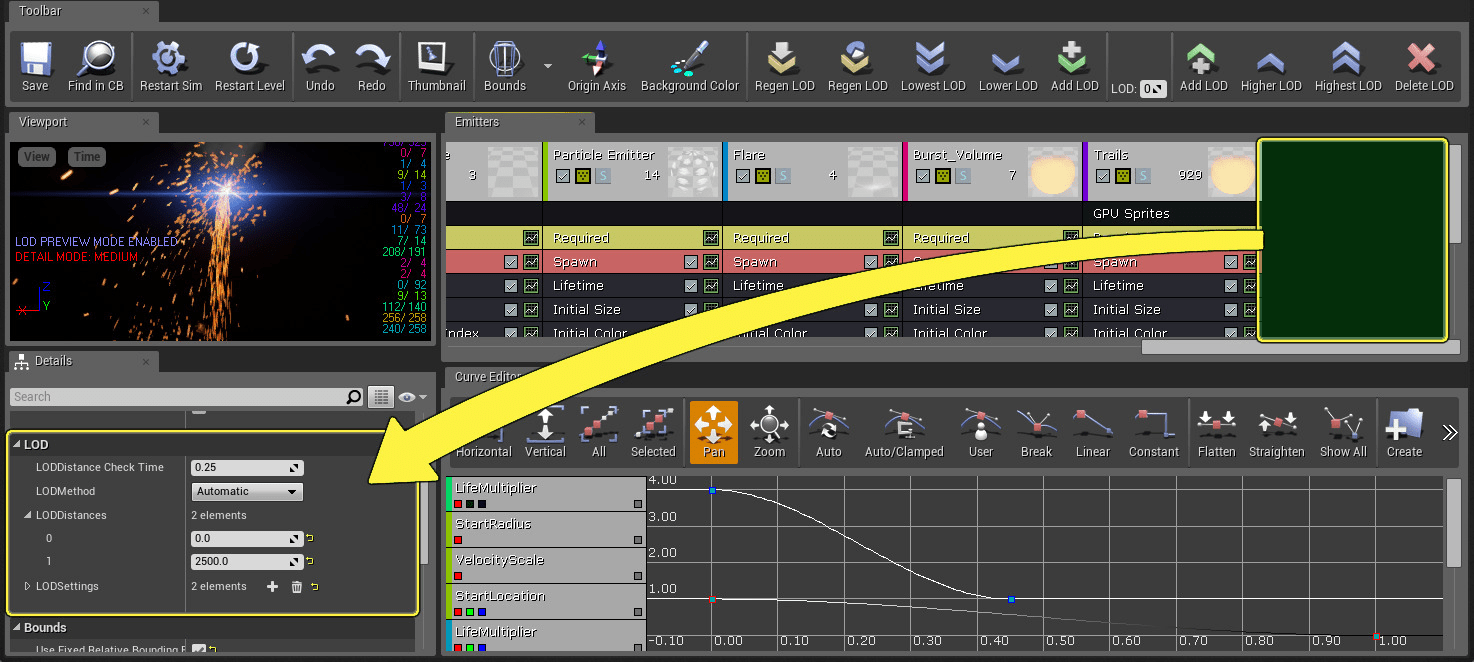
Physical Simulation

  • Final Project
  • Vislab Tour

Are particle systems used in games?

From the Unreal Engine documentation

Will physics simulations always be imperfect?

Never say never, but....

Are physics engines usually built separately from graphics engines?

This varies historically. It is possible to build them separately, whether separate ones are used or not tends to fluctuate.

Can we adjust explicit Euler to avoid deviations?

Yes, this leads to other so-called time integration techniques like:

  • Velocity Verlet
  • Runge-Kutta
  • Crank-Nicolson

Why is cloth so hard to simulate?

Cloth is almost-inextensible.

 

If we had exactly rigid cloth (e.g. Mylar) or very stretchy cloth (think spandex but way stretchier) this would be easy.

What's the difference in speed between 2D and 3D simulations?

Almost nothing*.

* terms and conditions apply

Are hacks like this standard for simulations?

void draw() {
  background(210);
  ellipse(250, y, r, r);
  accel = gravity;
  vel += accel;
  vel -= coef_fric * vel;
  y += vel;
  if (y > (height - r)) {
    vel = -(coef_rest * vel);
    y = height - r; // Massive hack
  }
}

You want to make your simulation as principled as possible.

 

But at some point, you'll find that the principle breaks down, or is too expensive to enforce.

What sort of techniques are used to reduce simulation costs?

This is an area of active research. Common ideas include:

 

  • Writing down the rules of physics in a different manner
  • Using better data structures to store information
  • Exploiting specialized hardware to do certain operations more quickly
  • Explicitly hand-calculating certain operations instead of doing them numerically for improved efficiency

Are there any downsides to using vectors over x,y forms?

Yes. They're less familiar and pack more details into fewer lines of code.

That's really about it.

There are also a few pitfalls you have to be aware of, like v1.add(v2) modifying v1.

Code Review

Equations of Motion

Equations of Motion

Equations that describe motions over time.

Newton's Second Law

F = ma

This is not solvable exactly on a computer for any interesting set of forces.

Not exactly solvable?

  1. Pull slightly on ball
  2. Start simulation
  3. Spring applies a restoring force
  4. Ball accelerates toward wall
  5. As soon as ball moves the slightest, the force on the ball changes. (???)

But we don't have a way to express "infinitely small amount" on a computer!

We need some way to discretize the simulation into timesteps and decide what happens in each timestep.

(Explicit) Euler's Method

  1. We are at \( \vec{x}\) with velocity \( \vec{v} \).
  2. Compute the update to our position
    • Take current velocity and multiply it by timestep duration
    • This is the step we'll take during the next timestep
  3. Compute the update to our velocity
    • Compute forces at our current location
    • Multiply acceleration by timestep
    • This is how much the velocity will change over the next timestep.

"Look at where we'll go next based off of where we are now"

\vec{x}^{i+1} = \vec{x}^i + \Delta t \cdot \vec{v}^i
\vec{v}^{i+1} = \vec{v}^i + \Delta t \cdot \vec{F}^i

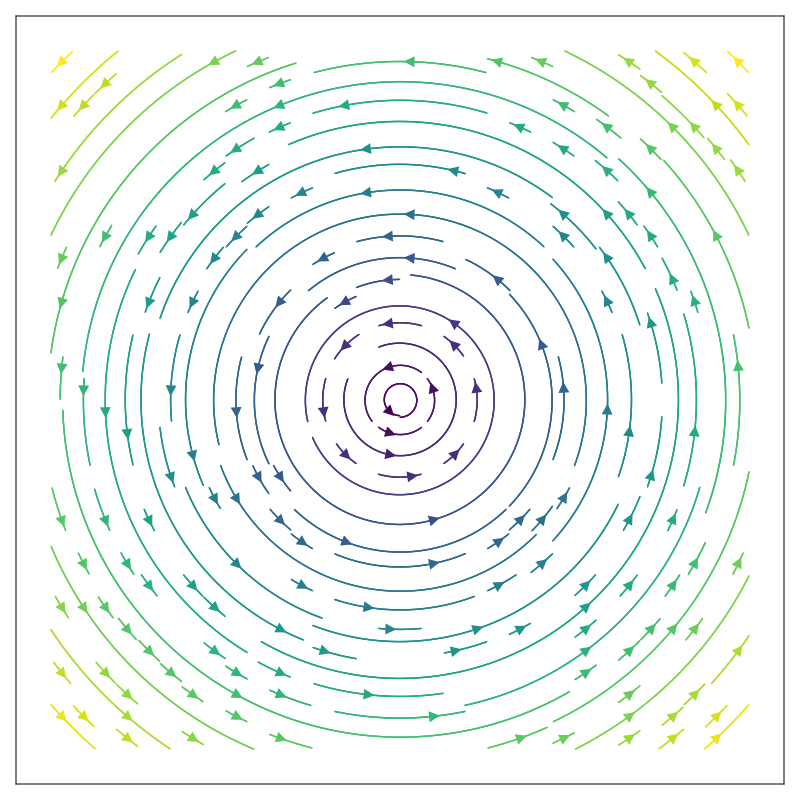
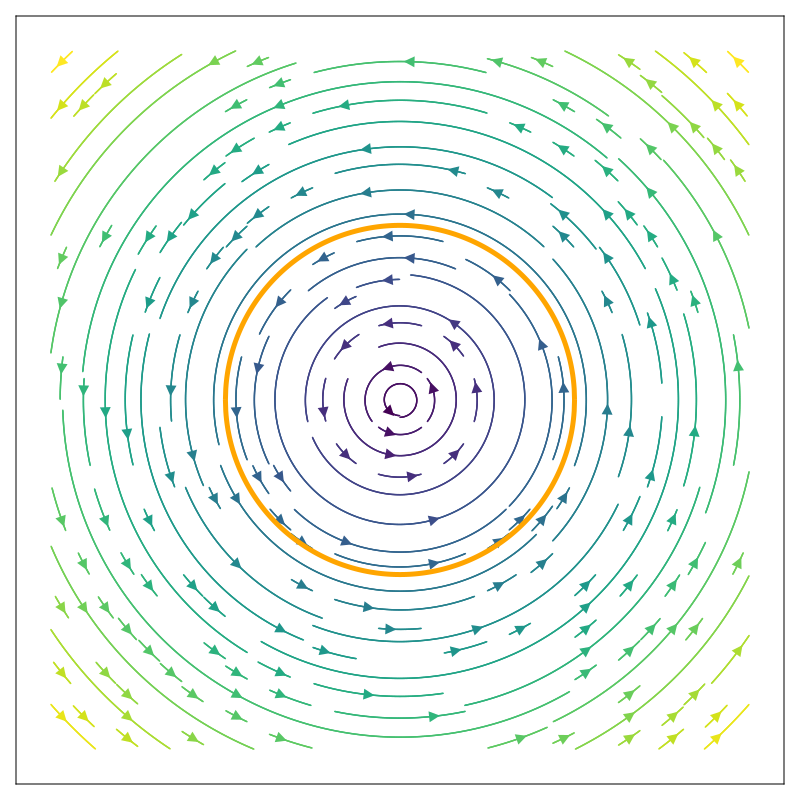
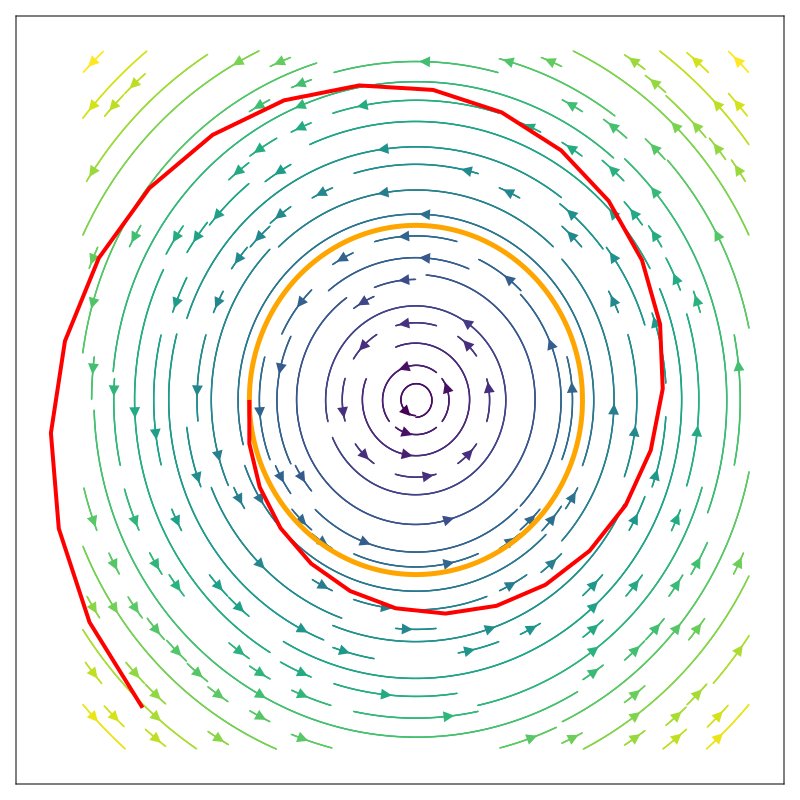
Issues with Explicit Euler

  • Requires very small timesteps to work.
    • Have to do much more computation to simulate the same amount of "real world" time.
  • Error tends to accumulate resulting in violation of conservation of energy (tends to lead to explodey systems).
  • Better, more stable methods exist, so explicit Euler is rarely used in practice
  • But it's simple to understand, and works well enough for our class!

Velocity Verlet

One of the methods often used in practice: it is not much more accurate, but it's still simple and doesn't suffer energy growth like the explicit Euler method does.

\vec{x}^{i+1} = \vec{x}^i + \Delta t \cdot \vec{v}^i
\vec{v}^{i+1} = \vec{v}^i + \Delta t \cdot \vec{F}^i
\vec{x}^{i+1} = \vec{x}^i + \Delta t \cdot \vec{v}^i + \frac{1}{2} \vec{a}^i \Delta t^2
\vec{v}^{i+1} = \vec{v}^i + \frac{\vec{a}^i + \vec{a}^{i+1}}{2} \Delta t

Explicit Euler

Velocity Verlet

where \( \vec{a} \) is the acceleration vector.

Other common methods: Runge-Kutta methods, Midpoint Euler

Accounting for Mass

We still haven't dealt with mass!

Our particle has a mass of \(m\).

The particle experiences a force of \(\vec{f}\).

\vec{f} = m \vec{a}

Solution: we need to divide the force by the mass to get the acceleration.

Particle with Mass

class Particle {
  float x;
  float vx;
  float mass;
 
 // ...

void advanceTime(float force, float dt){
  float accel = force / this.mass;

  this.x += this.vx * dt;
  this.vx += accel * dt;
}

Springs

Spring Forces

The force a spring exerts on its endpoints is based on:

  • Spring stiffness (\(k\))
  • Stretch from resting position (\(x\))

 

Hooke's Law tells us that the force is \( F = -k x\).

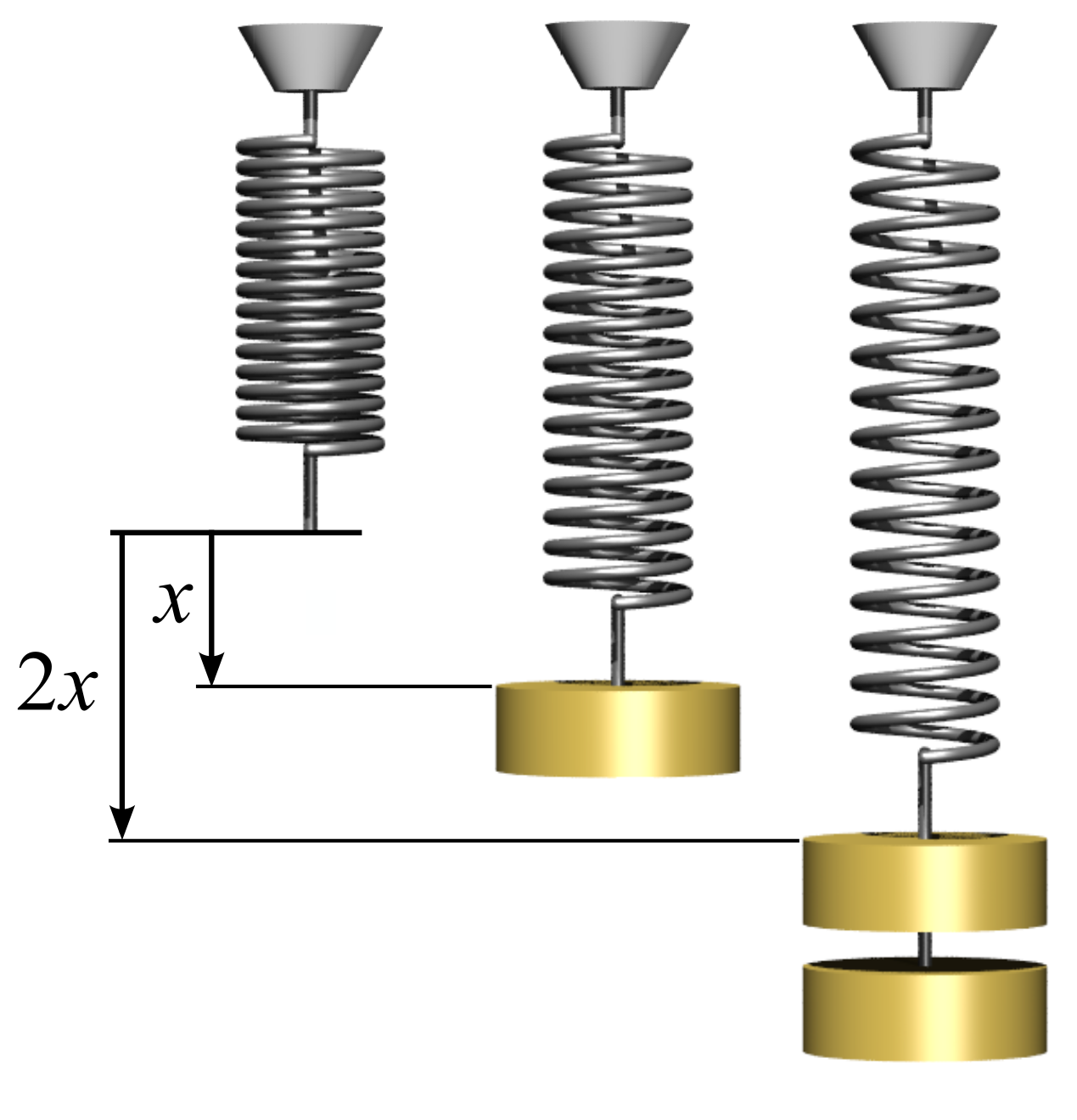
By Svjo - Own work, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=25398333

Spring Example

float y = 100.0;
float vy = 0.0;
float m = 1.0;
float ry = 250;
float ks = 1.0;
float dt = 0.1;

void setup() {
  size(500, 500);
  rectMode(CENTER);
}

void draw() {
  background(210);
  fill(0);
  ellipse(200, ry, 50, 50);
  float f = -(ks * (y - ry));
  float a = f/m;
  vy = vy + dt*a;
  y += dt*vy;
  line(200,ry,200,y);
  rect(200, y, 100, 20);
}

Question: what does ry represent in this code?

Damping

This spring system oscillates forever (the spring doesn't dissipate any energy).

 

That's not necessarily bad!

Sometimes, we want vibrations to "damp" out, i.e. get weaker and weaker until they stop.

How can we introduce damping into our spring?

Damping

F = -k_sx - k_d v

Spring force: tries to restore spring to its resting length.

Damping force: acts against motion of the spring

Damping

float y;
float vy;
float m = 1.0;
float ry = 250;
float ks = 0.1;
float kd = 0.1;

void setup() {
  size(500, 500);
}
void draw() {
  background(210);
  
  float f = -((ks * (y - ry)) + kd*vy);
  float a = f/m;
  vy = vy + a;
  y += vy;
  
  rect(200, y, 100, 20);
}

Extensions of Springs

All our springs so far have been zero restlength. Realistic springs have restlength of greater than zero.

Sequences of springs can simulate:

  • Hair
  • Rope
  • Grass

Networks of springs can simulate cloth.

Timestepping and Stiffness

Consider the following

Timestep 0

Consider the following

Timestep 1

Consider the following

Timestep 2

Consider the following

Timestep 3

Consider the following

Timestep 4

Consider the following

Uh oh....

If the timestep is too large

We can enter a cycle where our forces spiral out of control.

Will always happen with a sufficiently large timestep, though things like the integrator and spring stiffness will play a role.

float y;
float vy;
float m = 1.0;
float ry = 250;
float ks = 100.0;
float dt = 2.0;

void setup() {
  size(500, 500);
}
void draw() {
  background(210);
  float f = -(ks * (y - ry)) + 0.05;
  float a = f/m;
  vy = vy + dt*a;
  y += dt*vy;
  rect(200, y, 100, 20);
}

Hands-On: Physical Sim

  • Modify your particle so that it can be connected to other particles (note: plural!) by a spring. Render such springs as a line between the center of the two particles.
  • Change your update rule so that the springs apply force to the particles.
  • Simulate the following system, with initial states such that the system exhibits movement.

Index Cards!

  1. Your name and EID.
     
  2. One thing that you learned from class today. You are allowed to say "nothing" if you didn't learn anything.
     
  3. One question you have about something covered in class today. You may not respond "nothing".
     
  4. (Optional) Any other comments/questions/thoughts about today's class.

Can we apply more complex physics in Processing?

How would we make collisions work with lots of particles?

Absolutely. Most physics is controlled by the complexity of your numeric code

Do PVectors work similarly in 3D?

Is array() the best way to access the vectors of PVector?

Yes. In fact, all PVectors are implicitly 3D (but the third component is zeroed out and ignored when you use them in a 2D fashion).

I might recommend using the .x, .y, and .z members of the vector.

How do we make the acceleration more subtle?

Why does calling an object draw() from draw() only run it once?

draw() is only a special name when it's at the top level of your Processing program.

// This function is special. It is
// called in a loop and there can
// only be one function named this
void draw(){


}
// None of these methods are special.
// As far as Processing cares, they're
// just ordinary methods, and could
// be named anything--the name "draw"
// is totally coincidental.
class A {
  void draw(){}
}

class B {
  void draw(){}
  void draw(int x){}
}

Particle systems dictate the movement and appearance of particles within the world.

Examples: smoke, water, fire, clouds, dust, galaxies, etc.

Particle Systems

Generally, there will be three "stages" in a particle system, though these can be thought more as decisions to make than as stages-in-time.

  1. Emission stage: we decide where/how particles are generated and their initial states.
     
  2. Simulation stage: we decide how particles are going to behave (what forces are going to act on them and whether they'll collide, etc.)
     
  3. Rendering stage: we decide how particles are going to be displayed to the user.

What decisions were made for each stage for these particle systems?

Fireworks

Snowstorm

Extending the Particle

Additional rules (usually written as methods) can make the behavior of our Particle class more complex and interesting:

  • Continuous generation of particles
  • Changes to particle appearance over time
  • Application of additional forces on particles
  • Changes in how particles are visualized

These things don't have to be physically based!

Linked from https://en.wikipedia.org/wiki/Particle_system#/media/File:Particle_Emitter.jpg

Differences in rendering can create a large difference in visual impact!