Transformations

Shapes and Hierarchies

Shapes form complex structures via hierarchies. These make it easier to manipulate structures.

How do we actually do the manipulations?

Example: We should be able to just rotate stick person's arm at the shoulder, and ball will move (instead of having to move everything individually).

Transformations

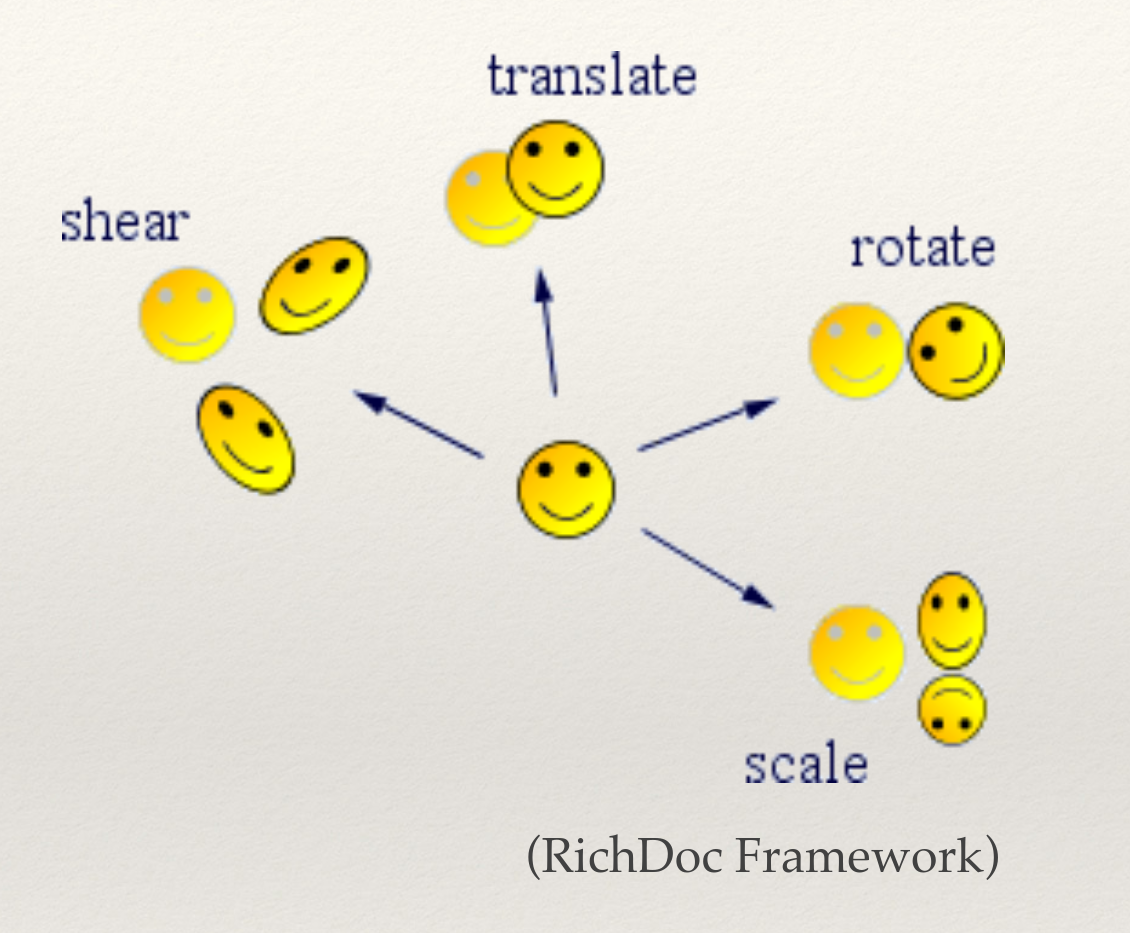
One of the foundations of rendering in computer graphics
Allow us to manipulate objects within a scene

Mathematical Representations

The field of linear algebra has deep connections to transformations in both 2D and 3D

Students spend their whole first month struggling with the linear algebra in spite of this.

In graphics for CS majors, we have a prerequisite of linear algebra for the course.

Representations

A point \(p\) is a vector:

p = \begin{bmatrix} x \\ y \end{bmatrix}

A transformation \(M\) is a matrix:

M = \begin{bmatrix} a & b \\ c & d \end{bmatrix}

We perform matrix multiplication to apply the transformation: \( p' = M p\)

\begin{bmatrix} x'\\ y' \end{bmatrix} = \begin{bmatrix} a & b \\ c & d \end{bmatrix} \begin{bmatrix} x\\ y \end{bmatrix}

Matrix Multiplication

\begin{bmatrix} x'\\ y' \end{bmatrix} = \begin{bmatrix} a & b \\ c & d \end{bmatrix} \begin{bmatrix} x\\ y \end{bmatrix}

x' = ax + by

y' = cx + dy

I = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}

What if we multiply by the so-called identity matrix?

Scaling

(1,1)

(2,2)

M_1 = \begin{bmatrix} 2 & 0 \\ 0 & 2 \end{bmatrix}

M_2 = \begin{bmatrix} 0.5 & 0 \\ 0 & 2 \end{bmatrix}

(2,2)

(4,4)

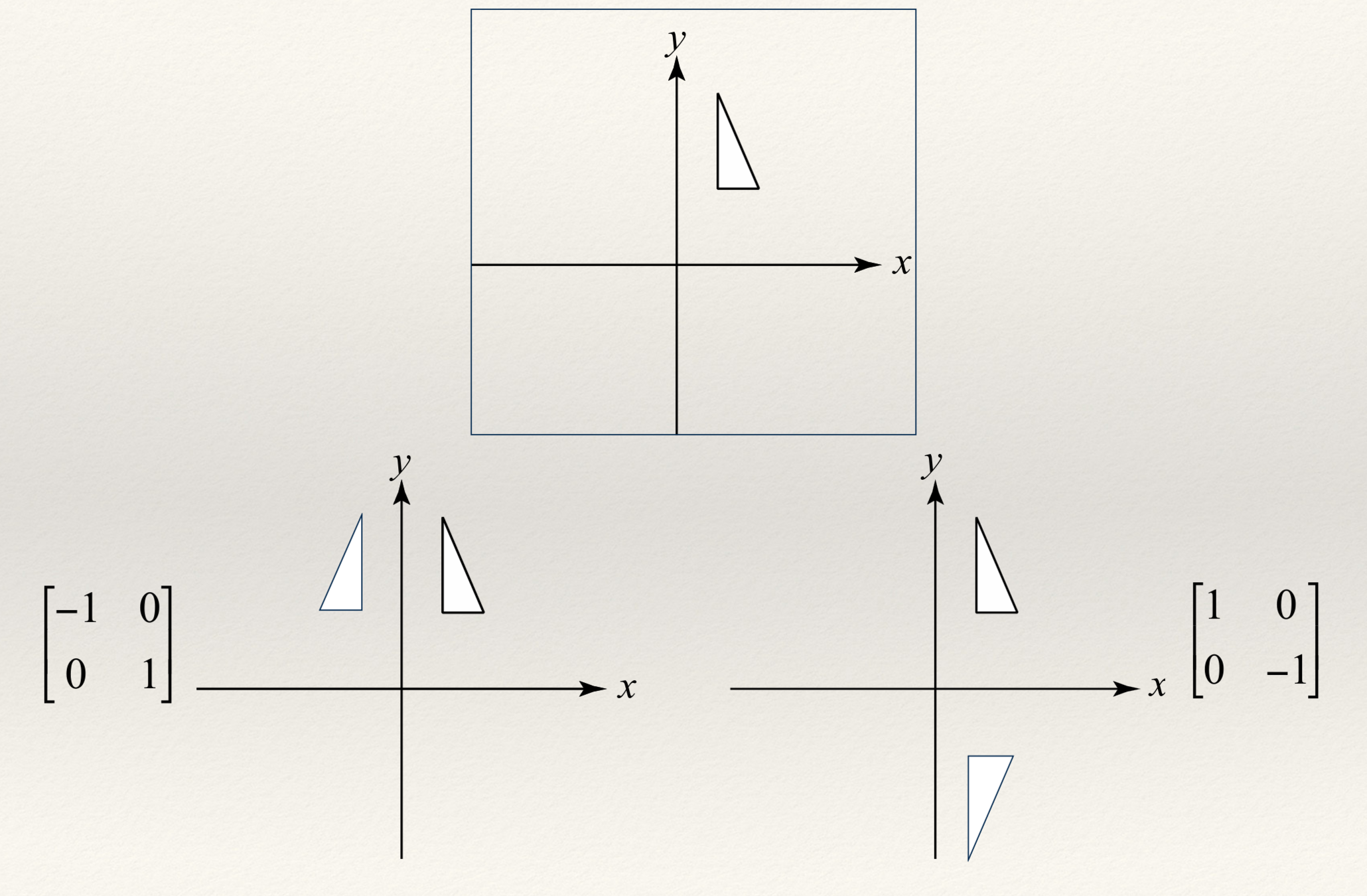
Reflection

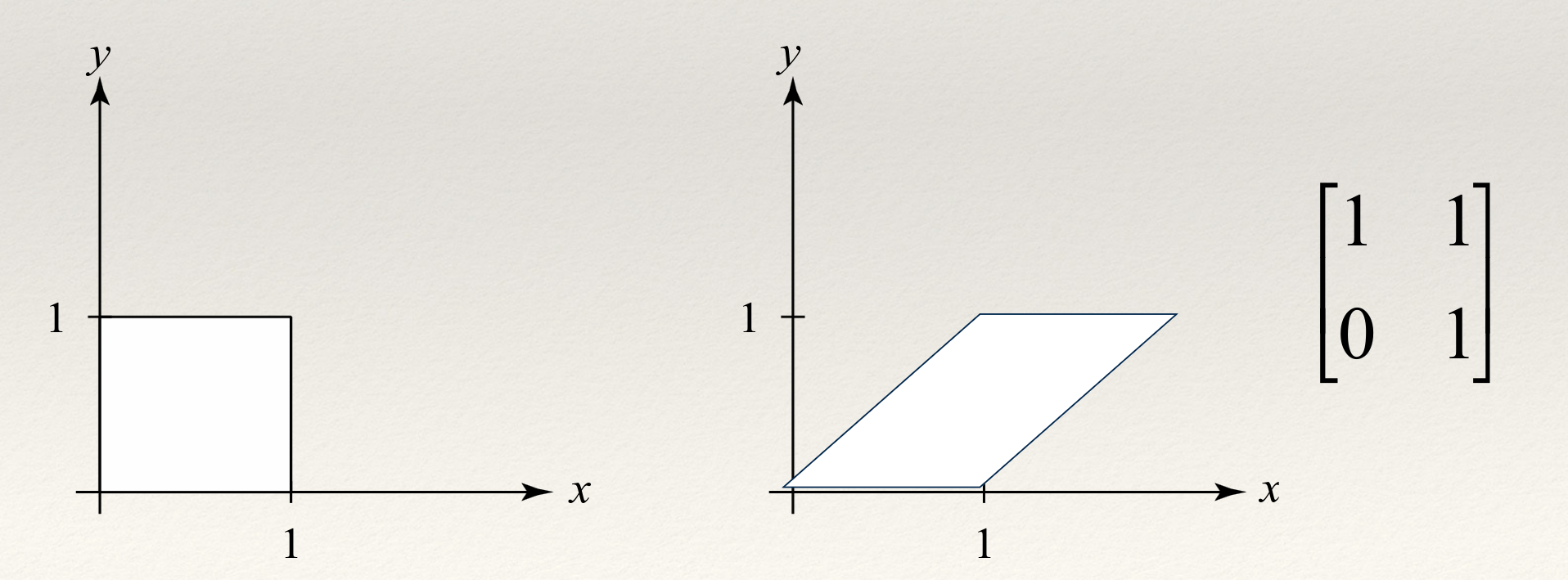
Shear

\begin{bmatrix} 1 & b\\ 0 & 1 \end{bmatrix}

x' = x + by

y' = y

Rotation

\theta

\begin{bmatrix} 1\\ 0 \end{bmatrix} \rightarrow \begin{bmatrix} \cos(\theta)\\ \sin(\theta) \end{bmatrix}

\begin{bmatrix} 0\\ 1 \end{bmatrix} \rightarrow \begin{bmatrix} -\sin(\theta)\\ \cos(\theta) \end{bmatrix}

M_r = R(\theta) = \begin{bmatrix} \cos(\theta) && -\sin(\theta)\\ \sin(\theta) && \cos(\theta) \end{bmatrix}

Linear Transformations

All of these transformations are considered linear transformations:

Scaling
Reflection
Shearing
Rotation

What very important operation is missing?

Translation

We want to be able to move objects through space.

But we can't do this using our standard linear algebra...

\begin{bmatrix} x'\\ y' \end{bmatrix} = \begin{bmatrix} a & b \\ c & d \end{bmatrix} \begin{bmatrix} 0\\ 0 \end{bmatrix}

Homogeneous Coordinates

\begin{bmatrix} x'\\ y'\\ 1 \end{bmatrix} = \begin{bmatrix} a & b & t_x\\ c & d & t_y\\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x\\y\\1 \end{bmatrix}

p' = M p

Combining Transformations

If we have a single, complex matrix, we can simply apply it to our object to get the resulting transform.

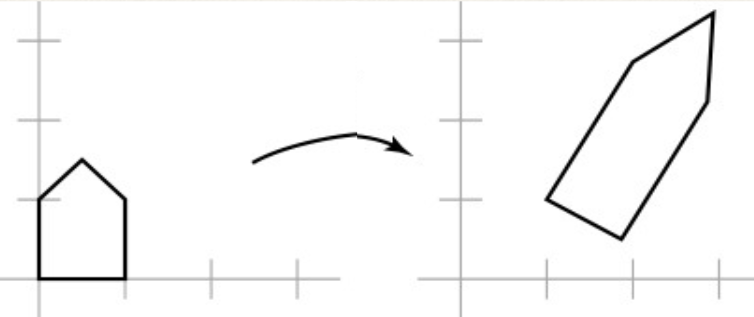
But we can (and often should!) think about it as a sequence of simpler transformations:

Order Matters!

Mathematical reason: matrix multiplication is generally not commutative.

Intuitive: what happens if we translate then reflect vs reflect then translate?

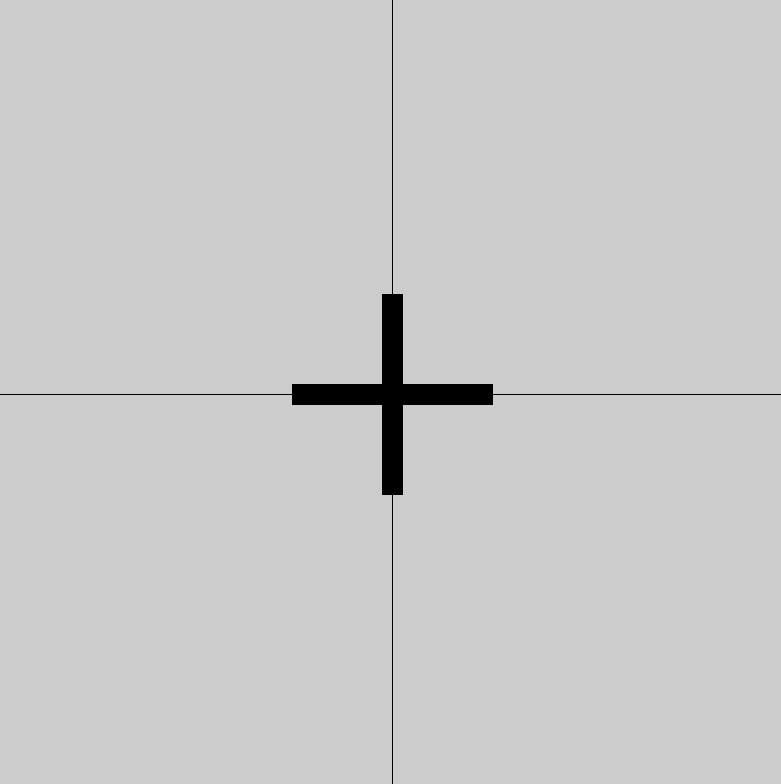
No Transformations Applied

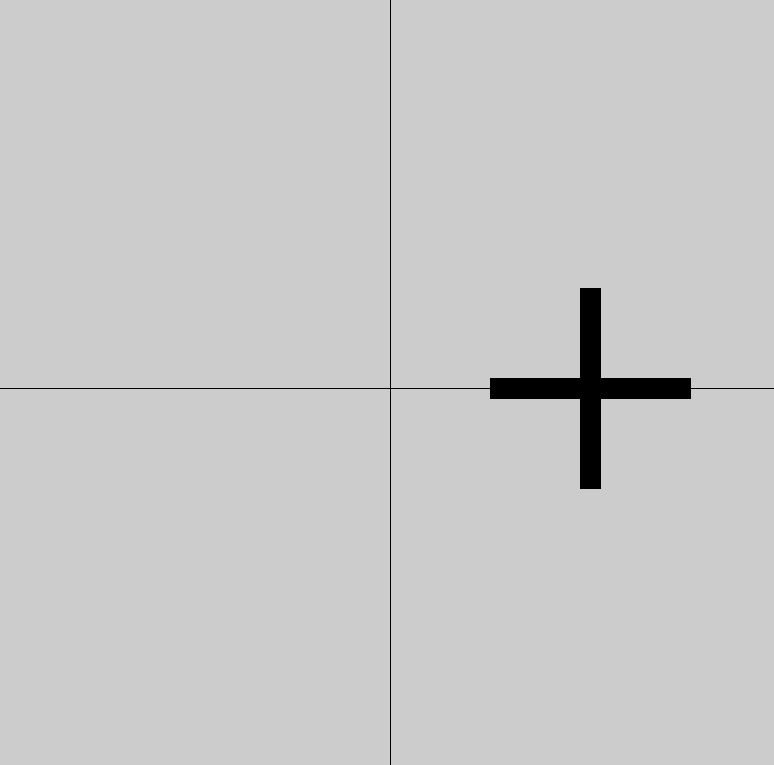
Translate Only

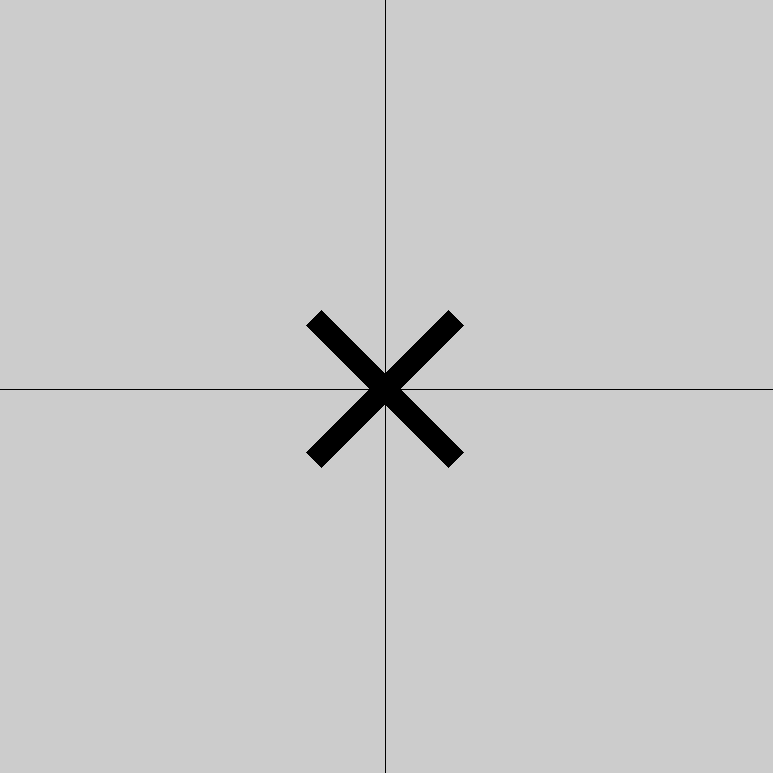
Rotate Only

translate()

rotate()

draw()

rotate()

translate()

draw()

Transformations in Processing

translate(x, y): applies a translation which moves points by (x,y)
rotate(θ): rotates by θ radians
scale(p): Scales by p, where 1.0 is no change.

Transformations in Processing

Transformations are a little like modes, where the transformation function affects all future draw calls.

Two major differences:

Transforms stack instead of replacing the previous transform.
The transform is reset at the top of the draw() loop.

void draw(){
  translate(100, 100);
  ellipse(0, 0, 100, 100);
  translate(200, 200);
  ellipse(0, 0, 60, 60);
  translate(300, 300);
  ellipse(0, 0, 35, 35);
}

Undoing Transformations

Ctrl+Z 101

Cancelling out a Transform

  rotate(radians(45));
  translate(200, 0);
  
  // Undo our transformation
  rotate(radians(-45));
  translate(-200, 0);

  shape(ref);

Wuh woh.

Shoes-Socks Theorem

Cancelling out a Transform, but properly

  rotate(radians(45));  // shoes
  translate(200, 0);    // socks
  
  translate(-200, 0);   // isocks
  rotate(radians(-45)); // ishoes

  shape(ref);

Bookmarking Transformations

Processing gives us tools to save and restore transformations.
pushMatrix() takes the current global transformation and records it in a matrix stack. You can think of this as a global variable that is hidden from you and can only be accessed with the functions here.
popMatrix() pops a transformation matrix off of the stack and makes it the current transformation matrix.
These functions let us manipulate objects at different levels in the scene hierarchy.

void draw(){
  pushMatrix();
  translate(100, 100);
  ellipse(0, 0, 100, 100);
  popMatrix();
  
  pushMatrix();
  translate(200, 200);
  ellipse(0, 0, 60, 60);
  popMatrix();
  
  pushMatrix();
  translate(300, 300);
  ellipse(0, 0, 35, 35);
  popMatrix();
}

Why Transformations?

We can already emulate scale by passing parameters to rect(). Why not just add a rotation parameter?

rect(0, 0, 100, 20, PI/8)

?

Composing transformations lets us describe very complex motion with simple code.

By author Zorgit on Wikimedia, CC-BY-SA 3.0: https://commons.wikimedia.org/wiki/File:Cycloid_f.gif

Composing transformations lets us describe very complex motion with simple code.

void draw(){  
  translate(300, 300);
  
  rotate(frameCount * 0.03);
  translate(50, 0);
  
  translate(30, 0);
  rotate(frameCount * 0.05);
  
  translate(10, 0);
  rotate(frameCount * 0.1);
  
  rect(0, 0, 100, 100);
}

In 3D, the "rotate" parameter gets complex

We need at least four* parameters to describe a rotation in three dimensions.

* terms and conditions apply

We need more spatial arguments as well!

box(x, y, z, width, height, depth, rot1, rot2, rot3, rot4);

In 3D, transformations are heavily used to avoid parameter explosions:

Boxes are always created at the origin
Spheres are always created at the origin
There are no ellipsoids (you have to scale a sphere)

Hands-On: Using Transformations

Translate the screen so that the origin (0,0) is at the center of the screen. Draw a solid black circle at (0,0) to demonstrate this.
Draw a shape of your choice. Before drawing it, translate, then rotate, then scale the shape (pick your own parameters for the transforms).
Draw the same shape as you did in step 2, with the same parameters for the transforms. However, this time, apply the scale first, then rotate, then translate.
Draw an object of your own choice and apply your own set of transformations to it.
OPTIONAL: Animate a rectangle orbiting your black circle using only transformations. See if you can keep the rectangle axis-aligned while it orbits!

The transformation in step 1 should apply to all of the other steps. For Steps 2-5, you may want to pushMatrix() and popMatrix() so that your transformations don't get too confusing.

Index Cards!

Your name and EID.
One thing that you learned from class today. You are allowed to say "nothing" if you didn't learn anything.
One question you have about something covered in class today. You may not respond "nothing".
(Optional) Any other comments/questions/thoughts about today's class.