PhD Proposal

Kevin Song

 

2024-03-19

Representations for Markovianity Detection

What is the nature of this motion?

  • Can the next location depend on previous locations, or does it only depend on the current location?
  • Is the motion random or deterministic?
  • Do the statistical properties of the motion change over time, or do they remain the same?

Dependence on history indicates incomplete knowledge of system!

Camera View

True System

Dependence on history indicates incomplete knowledge of system!

Camera View

True System

Dependence on history indicates incomplete knowledge of system!

Camera View

True System

Dependence on history indicates incomplete knowledge of system!

Camera View

True System

Dependence on history indicates incomplete knowledge of system!

Camera View

True System

Now that we've just seen a state change on the camera, are we more likely to see the particle continue through, or return to its old state?

Dependence on history indicates incomplete knowledge of system!

Camera View

True System

Now that we've just seen a state change on the camera, are we more likely to see the particle continue through, or return to its old state?

Dependence on history indicates incomplete knowledge of system!

Camera View

True System

Now that we've just seen a state change on the camera, are we more likely to see the particle continue through to the next state, or return to the old state?

Continue through

Dependence on history indicates incomplete knowledge of system!

Camera View

True System

Now that we've just seen a state change on the camera, are we more likely to see the particle continue through to the next state, or return to the old state?

Continue through

Return

Dependence on history indicates incomplete knowledge of system!

Camera View

True System

Now that we've just seen a state change on the camera, are we more likely to see the particle continue through to the next state, or return to the old state?

Continue through

Return

Appears that particle remembers its old state!

Which system results from incomplete observation?

Detecting behavior with memory allows us to conclude that we do not have a full picture of the system.

Microscopic systems are stochastic in nature.

Can be mathematically described by a stochastic process.

\{X_i\}

A set of random variables indexed by a time variable \(i \in \mathcal{T}\), with outcome space \(\mathcal{X}\)

\mathcal{T} \in \mathbb{R}^+, \mathcal{X} \subseteq \mathbb{R}^2
\mathcal{T} = \mathbb{N}, \mathcal{X} \subset \mathbb{N}

For now, we'll focus on discrete-time, discrete-space processes.

How much memory does a process have?

X_i
X_{i-1}
X_{i-2}
X_{i-3}
X_{i-k}

. . .

. . .

Which of these variables can affect the present (\(X_i\))?

TIME

Which of these variables can affect the present (\(X_i\))?

Can affect \(X_i\)

Do not affect \(X_i\)

A process with no memory.

X_i
X_{i-1}
X_{i-2}
X_{i-3}
X_{i-k}

. . .

. . .

Can affect \(X_i\)

Do not affect \(X_i\)

A process with moderate memory.

X_i
X_{i-1}
X_{i-2}
X_{i-3}
X_{i-k}

. . .

. . .

Which of these variables can affect the present (\(X_i\))?

Can affect \(X_i\)

Do not affect \(X_i\)

A process with long memory.

X_i
X_{i-1}
X_{i-2}
X_{i-3}
X_{i-k}

. . .

. . .

Which of these variables can affect the present (\(X_i\))?

Can affect \(X_i\)

A process with infinite memory.

X_i
X_{i-1}
X_{i-2}
X_{i-3}
X_{i-k}

. . .

. . .

Which of these variables can affect the present (\(X_i\))?

p(X_i = x_i | X_{i-1} = x_{i-1}, X_{i-2} = x_{i-2}, \dots, X_1 = x_1)
= p(X_i = x_i | X_{i-1} = x_{i-1})

Formally: require certain conditions on probabilities

This condition specifies a Markov process

Can affect \(X_i\)

Do not affect \(X_i\)

X_i
X_{i-1}
X_{i-2}
X_{i-3}
X_{i-k}

. . .

. . .

Discrete-Time Memory

The next state of the stochastic process depends on the previous \(n\) values, but nothing more.

A category of stochastic processes referred to as \(n\)-Markov.

Important note: if \(n \geq 2\), the process is considered "non-Markov"

p(X_i = x_i | X_{i-1} = x_{i-1}, \dots, X_{i-n} = x_{i-n}, X_{i-n-1}, \dots X_1 = x_1)
= p(X_i = x_i | X_{i-1} = x_{i-1}, \dots, X_{i-n} = x_{i-n})

A note on Shorthand

Writing out the names of all the random variables and the outcomes leads to a lot of visual noise.

 

We will often use just the lowercase outcome names and implicitly use them as the outcome of the random variable with the same uppercase name.

p(x_i | x_{i-1}, \dots, x_{i-n}, \dots x_1)= p(x_i | x_{i-1}, \dots, x_{i-n})
p(X_i = x_i | X_{i-1} = x_{i-1}, \dots, X_{i-n} = x_{i-n}, X_{i-n-1}, \dots X_1 = x_1)
= p(X_i = x_i | X_{i-1} = x_{i-1}, \dots, X_{i-n} = x_{i-n})

Given observations \( x_1, x_2, \dots, x_N \) of a stochastic process \( X_i \), how can we tell whether \( X_i \) is a Markov process?

If \(X_i\) is non-Markov, can we bound how large \(n\) is?

Can the next location depend on previous locations, or does it only depend on the current location?

Prior Work

Could check that the \(n\)-Markov equality is satisfied...

...but we don't have the actual probabilities, just samples!

If we use empirical probabilities, the equality will rarely ever be satisfied for the same reason that tossing 100 coins rarely results in 50 heads and 50 tails.

p(x_i | x_{i-1}, \dots, x_{i-n}, \dots x_1)= p(x_i | x_{i-1}, \dots, x_{i-n})

Two Camps

Model Fitting

Markov in-principle

  • Take experimental data and fit it to some presumed model of dynamics (e.g. diffusion with heavy/light particle)
     
  • If fit to experimental statistics is good, then system is well-described by that model.
     
  • System shares same Markov or non-Markov behavior as the model.
  • Establish some necessary condition for the system to be Markov.
     
  • Determine whether the system meets this condition or not.

Model Fitting

(2) Sokolov, Igor M. 2012. “Models of Anomalous Diffusion in Crowded Environments.” Soft Matter 8 (35): 9043–52.

Metzler, Ralf, and Joseph Klafter. 2000. “The Random Walk’s Guide to Anomalous Diffusion: A Fractional Dynamics Approach.” Physics Reports 339 (1): 1–77.

Muñoz-Gil, Gorka, Giovanni Volpe, Miguel Angel Garcia-March, Erez Aghion, Aykut Argun, Chang Beom Hong, Tom Bland, et al. 2021. “Objective Comparison of Methods to Decode Anomalous Diffusion.” Nature Communications 12 (1): 6253.

(1) Dudko, Olga K., Gerhard Hummer, and Attila Szabo. 2006. “Intrinsic Rates and Activation Free Energies from Single-Molecule Pulling Experiments.” Physical Review Letters 96 (10): 108101.

Dudko, Olga K., Gerhard Hummer, and Attila Szabo. 2008. “Theory, Analysis, and Interpretation of Single-Molecule Force Spectroscopy Experiments.” Proceedings of the National Academy of Sciences of the United States of America 105 (41): 15755–60.

Best, Robert B., and Gerhard Hummer. 2011. “Diffusion Models of Protein Folding.” Physical Chemistry Chemical Physics: PCCP 13 (38): 16902–11.

(1) Barrier Crossing

(2) Sticky Walk

Problems with Model Fitting

If fit is perfect, everything is fine!

(side note: this never happens)

Relies on experimenter intuition to construct the appropriate models!

If fit is not perfect, is this because the data is noisy, or because there's a better model that we haven't discovered?

Markov in-principle

Berezhkovskii, Alexander M., and Dmitrii E. Makarov. 2018. “Single-Molecule Test for Markovianity of the Dynamics along a Reaction Coordinate.” Journal of Physical Chemistry Letters 9 (9): 2190–95.

a
b
x
P(a \to b | x)
P(a \to a | x)
x
x
x
x
x

Markov in-principle

Berezhkovskii, Alexander M., and Dmitrii E. Makarov. 2018. “Single-Molecule Test for Markovianity of the Dynamics along a Reaction Coordinate.” Journal of Physical Chemistry Letters 9 (9): 2190–95.

a
b
x
x
x
x
x
x
\min_x P(a \to a | x) = 1/2
\max_x P(a \to b | x) = 1/4

Other Criteria

How wide can the distribution of transition path times be?

If they're wider than a certain cutoff, the dynamics result from projection of multidimensional dynamics onto 1D.

Satija, Rohit, Alexander M. Berezhkovskii, and Dmitrii E. Makarov. 2020. “Broad Distributions of Transition-Path Times Are Fingerprints of Multidimensionality of the Underlying Free Energy Landscapes.” Proceedings of the National Academy of Sciences of the United States of America 117 (44): 27116–23.

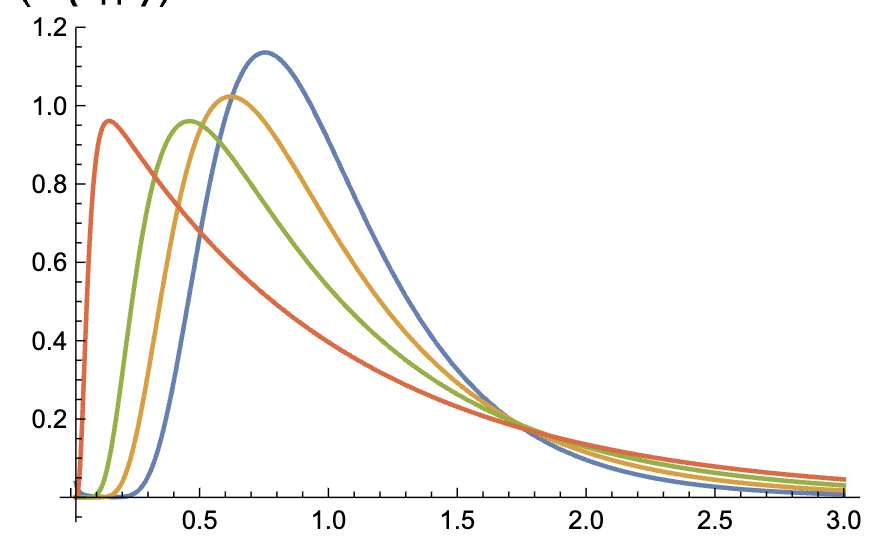
Transition Path (TP) Time

Probability of TP Time

(1) Zijlstra, Niels, Daniel Nettels, Rohit Satija, Dmitrii E. Makarov, and Benjamin Schuler. 2020. “Transition Path Dynamics of a Dielectric Particle in a Bistable Optical Trap.” Physical Review Letters 125 (14): 146001.

(2) Makarov, Dmitrii E. 2021. “Barrier Crossing Dynamics from Single-Molecule Measurements.” The Journal of Physical Chemistry. B 125 (10): 2467–76.

(3) Lapolla, Alessio, and Aljaž Godec. 2021. “Toolbox for Quantifying Memory in Dynamics along Reaction Coordinates.” Physical Review Research 3 (2): L022018.

Cannot quantify the order of memory in the case where the system is found to be non-Markov.

Cannot be used in cases where the observable is a discrete random variable.

Ideas from Information Theory

Entropy

H(X) = -\sum\limits_{x \in \mathcal{X}} p(x) \log p(x)

"How hard is it to guess the next symbol?"

Easy (low entropy)

Hard (high entropy)

p(x)
x
p(x)
x
p(x)
x

Entropy Sets a Communication Limit

x
X

Entropy Sets a Communication Limit

x_1 \sim
X

Entropy Sets a Communication Limit

x_1
X

Entropy Sets a Communication Limit

x_1
X

Entropy Sets a Communication Limit

X
x_1

Entropy Sets a Communication Limit

X
x_1
x_2

Entropy Sets a Communication Limit

X
x_1
x_2 \sim

Entropy Sets a Communication Limit

X
x_1
x_2

Entropy Sets a Communication Limit

X
x_1
x_2

Entropy Sets a Communication Limit

X
x_1
x_2
x_3

Entropy Sets a Communication Limit

X
x_1
x_2
x_3 \sim

Entropy Sets a Communication Limit

X
x_1
x_2
x_3

Entropy Sets a Communication Limit

X
x_1
x_2
x_3

Entropy Sets a Communication Limit

X
x_1
x_2
x_3

Entropy Sets a Communication Limit

x_1
x_2
x_3

Let's say we repeat this process \(N\) times. How many bits do we need to send over the wire?

... x_N
X

Entropy Sets a Communication Limit

x_1
x_2
x_3

Let's say we repeat this process \(N\) times. How many bits do we need to send over the wire?

... x_N

Ease of prediction translates to ease of communication!

Shannon's source coding theorem

\( H(X) \) bits per observation

Removing Independence

The source coding theorem assumes that the variables occur i.i.d. But this is typically not the case in practice!

 tr__

 buried

Removing Independence

The source coding theorem assumes that the variables occur i.i.d. But this is typically not the case in practice!

 tr__

 buried

A pirate found

Removing Independence

The source coding theorem assumes that the variables occur i.i.d. But this is typically not the case in practice!

 tr__

 buried

A pirate found

Knowledge of earlier symbols makes it easier to guess what comes next.

Conditional Entropy

H(X_2 | X_1)

How easy is it to guess \(X_2\) if I already know the value of \(X_1\)?

h^{(k)}(\{X_i\}) = H(X_n | X_{n-1}, X_{n-2}, \dots X_{n-k})

Define the \(k\)-th order (conditional) entropy by:

How easy is it to guess the next symbol if I've seen the value of the previous \(k\) symbols?

tr__

buried tr__

A pirate found buried tr__

h^{(2)}
h^{(9)}
h^{(24)}

Conditioning on more variables makes it no harder to guess!

h^{(k+1)} \leq h^{(k)}

. . .

. . .

X_i
X_{i-1}
X_{i-2}
X_{i-3}
X_{i-n}
h^{(1)}

Suppose \( \{X_i\}\) is a Markov process of order \(n\), i.e. an \(n\)-Markov process).

Does \(h^{(k)}\) ever stop decreasing? 

h^{(1)}
h^{(2)}

Suppose \( \{X_i\}\) is a Markov process of order \(n\), i.e. an \(n\)-Markov process).

Does \(h^{(k)}\) ever stop decreasing? 

h^{(1)}
h^{(2)}

. . .

. . .

X_i
X_{i-1}
X_{i-2}
X_{i-3}
X_{i-n}
h^{(3)}

Suppose \( \{X_i\}\) is a Markov process of order \(n\), i.e. an \(n\)-Markov process).

Does \(h^{(k)}\) ever stop decreasing? 

h^{(1)}
\geq
h^{(2)}

. . .

. . .

X_i
X_{i-1}
X_{i-2}
X_{i-3}
X_{i-n}
h^{(n)}

Suppose \( \{X_i\}\) is a Markov process of order \(n\), i.e. an \(n\)-Markov process).

Does \(h^{(k)}\) ever stop decreasing? 

h^{(1)}
\geq
h^{(2)}

. . .

. . .

X_i
X_{i-1}
X_{i-2}
X_{i-3}
X_{i-n}
h^{(3)}
\geq

...

h^{(n+1)}

Suppose \( \{X_i\}\) is a Markov process of order \(n\), i.e. an \(n\)-Markov process).

Does \(h^{(k)}\) ever stop decreasing? 

h^{(1)}
\geq
h^{(2)}

. . .

. . .

X_i
X_{i-1}
X_{i-2}
X_{i-3}
X_{i-n}
h^{(3)}
\geq

...

h^{(n)}
\geq
h^{(n+2)}

Suppose \( \{X_i\}\) is a Markov process of order \(n\), i.e. an \(n\)-Markov process).

Does \(h^{(k)}\) ever stop decreasing? 

h^{(1)}
\geq
h^{(2)}

. . .

. . .

X_i
X_{i-1}
X_{i-2}
X_{i-3}
X_{i-n}
h^{(3)}
\geq

...

h^{(n)}
\geq
h^{(n+1)}
=
h^{(n+2)}

Suppose \( \{X_i\}\) is a Markov process of order \(n\), i.e. an \(n\)-Markov process).

Does \(h^{(k)}\) ever stop decreasing? 

h^{(1)}
\geq
h^{(2)}

. . .

. . .

X_i
X_{i-1}
X_{i-2}
X_{i-3}
X_{i-n}
h^{(3)}
\geq

...

h^{(n)}
\geq
h^{(n+1)}
=
h^{(n+2)}
=

...

=

Suppose \( \{X_i\}\) is a Markov process of order \(n\), i.e. an \(n\)-Markov process).

Does \(h^{(k)}\) ever stop decreasing? 

. . .

. . .

X_i
X_{i-1}
X_{i-2}
X_{i-3}
X_{i-n}

For an \(n\)-th order Markov process

h^{(k)} = h^{(n)}

for \(k > n\)

k
h^{(k)}
k
h^{(k)}

n-Markov

Infinite Memory

h^{(k+1)} \leq h^{(k)}
h^{(k)} = h^{(n)}

for an \(n\)-Markov process for \(k > n\)

Special Case: Markov

k
h^{(k)}

Estimating \(h^{(k)}\)

How do we actually estimate \(h^{(k)}\)?

Count!

To evaluate the formula for \(h^{(k)}\), we need probabilities of seeing \(k\)-grams and \(k+1\)-grams.

Use empirical frequencies as a proxy for these probabilities.

How do we actually estimate \(h^{(3)}\)?

122121212212222211111222112122112222221111221

How do we actually estimate \(h^{(3)}\)?

122121212212222211111222112122112222221111221

Frequency

Sequence

How do we actually estimate \(h^{(3)}\)?

122121212212222211111222112122112222221111221

Frequency

Sequence

[

How do we actually estimate \(h^{(3)}\)?

122121212212222211111222112122112222221111221

Frequency

Sequence

[

1 2 2

1

How do we actually estimate \(h^{(3)}\)?

122121212212222211111222112122112222221111221

Frequency

Sequence

[

1 2 2

1

2 2 1

1

How do we actually estimate \(h^{(3)}\)?

122121212212222211111222112122112222221111221

Frequency

Sequence

[

1 2 2

1

2 2 1

1

2 1 2

1

How do we actually estimate \(h^{(3)}\)?

122121212212222211111222112122112222221111221

Frequency

Sequence

[

1 2 2

1

2 2 1

1

2 1 2

1

1 2 1

1

How do we actually estimate \(h^{(3)}\)?

122121212212222211111222112122112222221111221

Frequency

Sequence

[

1 2 2

1

2 2 1

1

2 1 2

2

1 2 1

1

How do we actually estimate \(h^{(3)}\)?

122121212212222211111222112122112222221111221

Frequency

Sequence

[

1 2 2

1

2 2 1

4

2 1 2

2

1 2 1

3

etc.

etc.

How do we actually estimate \(h^{(3)}\)?

122121212212222211111222112122112222221111221

Frequency

Sequence

[

1 2 2

2 2 1

2 1 2

1 2 1

etc.

etc.

1 2 2 1

1

1

4

2

3

How do we actually estimate \(h^{(3)}\)?

122121212212222211111222112122112222221111221

Frequency

Sequence

[

1 2 2

2 2 1

2 1 2

1 2 1

etc.

etc.

1 2 2 1

1

2 2 1 2

1

1

4

2

3

How do we actually estimate \(h^{(3)}\)?

122121212212222211111222112122112222221111221

Frequency

Sequence

[

1 2 2

2 2 1

2 1 2

1 2 1

etc.

etc.

1 2 2 1

2

2 2 1 2

1

and so on

and so forth

1

4

2

3

How do we actually estimate \(h^{(3)}\)?

122121212212222211111222112122112222221111221

Frequency

Sequence

[

1 2 2

2 2 1

2 1 2

1 2 1

etc.

etc.

1 2 2 1

2

2 2 1 2

1

and so on

and so forth

1

4

2

3

How do we actually estimate \(h^{(3)}\)?

Frequency

Sequence

1 2 2

1

2 2 1

4

2 1 2

2

1 2 1

3

1 2 2 1

2

2 2 1 2

1

Probability

1/37

4/37

2/37

3/37

2/38

1/38

Plug these probabilities directly into the formula for conditional entropy.

 

Known as the plug-in or histogram estimator.

Plug-in estimators have a serious flaw!

Dębowski, Łukasz. 2016. “Consistency of the Plug-in Estimator of the Entropy Rate for Ergodic Processes.” In 2016 IEEE International Symposium on Information Theory (ISIT), 1651–55. IEEE.

We need at least \(2^{k H(X)}\) points to get an correct estimator of \(h^{k}\).

If we use plug-in estimators, we can always conclude a process is non-Markov. Just pick a large enough \(k\).

p(x_i | x_{i-1}, \dots, x_{i-n}, \dots x_1)= p(x_i | x_{i-1}, \dots, x_{i-n})

Plug-in Estimators Cover Small \(k\)

...

Plug-in estimators work well here!

k

Compression?

h(\{X_i\}) = \lim_{k \to \infty} h^{(k)}\left( \{X_i\} \right)

The minimum number of bits needed to communicate a new observation of \(X_i\) given the complete history of \(X_i\) so far.

Compression algorithms seem to be a good candidate for estimating this value:

  • Provable eventual convergence for LZ77 family
  • Many high-quality, high-speed implementations (GZIP, GIF, 7ZIP)

Compress the output, see how many bits (on average) are needed to represent each observation, then use this as a proxy for \(h\).

Compression Covers Infinite \(k\)

...

Plug-in estimators work well here!

Compression works well here!

\infty
k

Compression Covers Infinite \(k\)

...

Plug-in estimators work well here!

Compression works well here!

\infty

What about here?

k

LZ77-family algorithms have \(O\left(\frac{\log \log N}{\log N}\right)\) convergence.

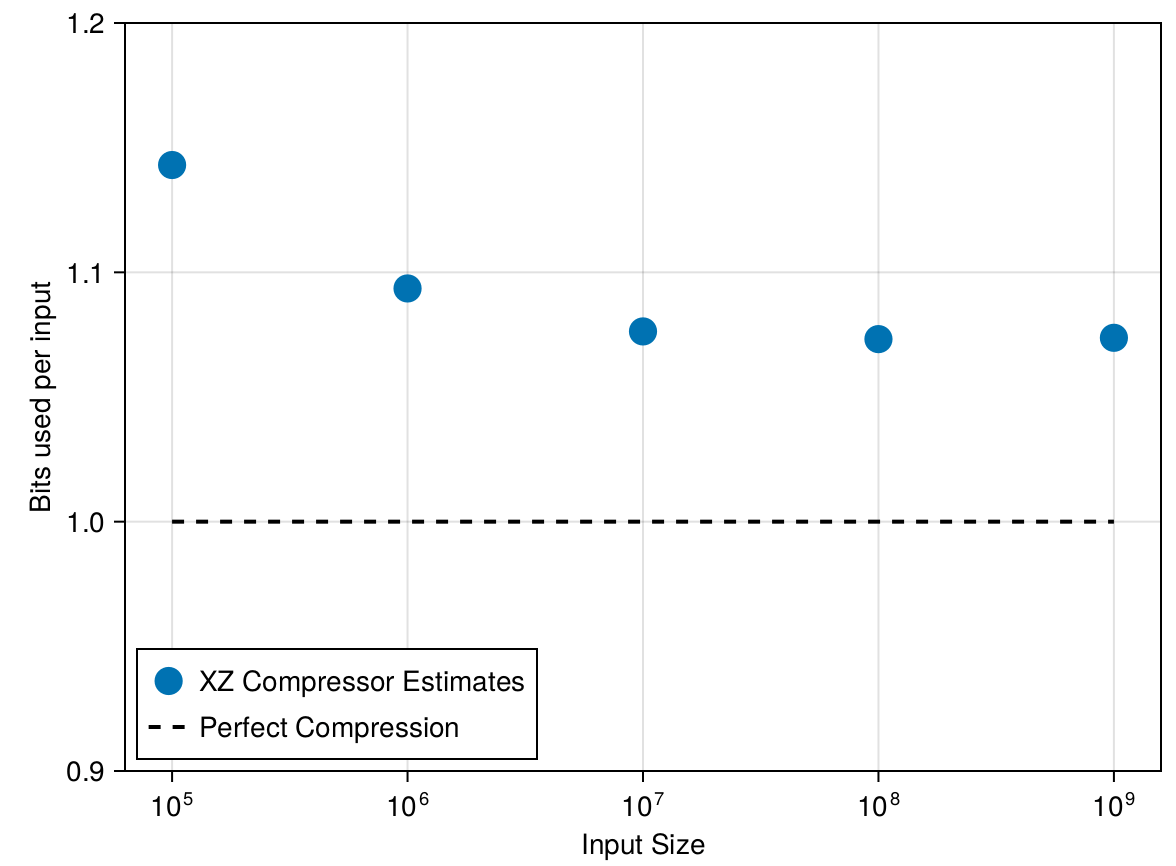
What to do?

Additional wrinkle: "eventually" really does mean eventually!

Convergence to small error not possible with any reasonable data size.

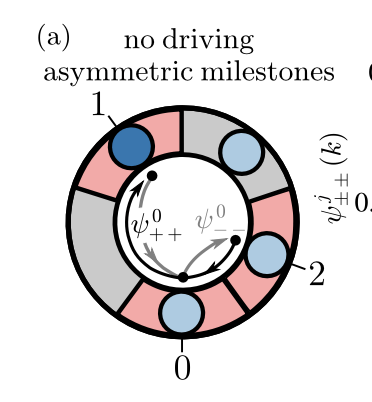
Discrete Markovianity Detection

Song, Kevin, Dmitrii E. Makarov, and Etienne Vouga. 2023. “Compression Algorithms Reveal Memory Effects and Static Disorder in Single-Molecule Trajectories.” Physical Review Research 5 (1): L012026.

Our Observation

Errors in the compression algorithm are empirically strongly dependent on the size of the input, and weakly dependent on the distribution.

Our Observation

The distributional difference between a \(k\)-Markov and \(k+1\)-Markov process is not that large for most physically-motivated processes.

Errors in the compression algorithm are empirically strongly dependent on the size of the input, and weakly dependent on the distribution.

Idea

Artificially generate a process which has the is known to be \(k\)-Markov, and compare it to the true (observed) process.

1221212122122222111112221121221122222211112212122121

12112212221212121212221221212121222221112221212122

Term Frequency Probability
... ... ...
... ... ...

Pick

\(k\)

Resample k-Markov process

Compress

Compress

\tilde{h}
\tilde{h}^{(k)}

=

?

h^{(\infty)} = h^{(k)}

Details here

Entropy Rate Estimator Correction

  1. Compressor error is not sensitive to small shifts in distribution
  2. Change between different Markov orders represents a small shift in distribution for processes of interest

Extra Credit: Try to recover the correct numerical value of \(h^{(k)}\)

Entropy Rate Estimator Correction

  1. Compressor error is not sensitive to small shifts in distribution
  2. Change between different Markov orders represents a small shift in distribution for processes of interest
\tilde{h}^{(1)}

\(h^{(1)}\) estimated by compression

Entropy Rate Estimator Correction

  1. Compressor error is not sensitive to small shifts in distribution
  2. Change between different Markov orders represents a small shift in distribution for processes of interest
\tilde{h}^{(1)}

\(h^{(1)}\) estimated by plug-in method. Can assume this is very accurate.

\tilde{h}^{(1)}
\hat{h}_p^{(1)}

\(h^{(1)}\) estimated by compression

Entropy Rate Estimator Correction

  1. Compressor error is not sensitive to small shifts in distribution
  2. Change between different Markov orders represents a small shift in distribution for processes of interest

The error in \(\tilde{h}^{(1)}\).

\tilde{h}^{(1)}
\hat{h}_p^{(1)}
-

Entropy Rate Estimator Correction

  1. Compressor error is not sensitive to small shifts in distribution
  2. Change between different Markov orders represents a small shift in distribution for processes of interest

Also the error in all the compressor estimates, since increasing \(k\) does not shift the error!

\tilde{h}^{(1)} - \hat{h}^{(1)}_p

The error in \(\tilde{h}^{(1)}\).

Entropy Rate Estimator Correction

  1. Compressor error is not sensitive to small shifts in distribution
  2. Change between different Markov orders represents a small shift in distribution for processes of interest

The error in \(\tilde{h}^{(k)}\)?

\tilde{h}^{(1)} - \hat{h}^{(1)}_p

Entropy Rate Estimator Correction

  1. Compressor error is not sensitive to small shifts in distribution
  2. Change between different Markov orders represents a small shift in distribution for processes of interest
\tilde{h}^{(k)}

The compressor estimate of \(h^{(k)}\).

\tilde{h}^{(1)} - \hat{h}^{(1)}_p

The error in \(\tilde{h}^{(k)}\)?

Entropy Rate Estimator Correction

  1. Compressor error is not sensitive to small shifts in distribution
  2. Change between different Markov orders represents a small shift in distribution for processes of interest
\tilde{h}^{(k)}
( \tilde{h}^{(1)} - \hat{h}^{(1)}_p )
-

Entropy Rate Estimator Correction

  1. Compressor error is not sensitive to small shifts in distribution
  2. Change between different Markov orders represents a small shift in distribution for processes of interest
\tilde{h}^{(k)}
( \tilde{h}^{(1)} - \hat{h}^{(1)}_p )
-

The exact \(k\)th order entropy?

h^{(k)} \stackrel{?}{=}

Entropy Rate Estimator Correction

  1. Compressor error is not sensitive to small shifts in distribution
  2. Change between different Markov orders represents a small shift in distribution for processes of interest
\tilde{h}^{(k)}
( \tilde{h}^{(1)} - \hat{h}^{(1)}_p )
-

The exact \(k\)th order entropy?

h^{(k)} \stackrel{?}{=}

Well....not always. But it comes out pretty close most of the time!

Results: Coarse-Grained Random Walk

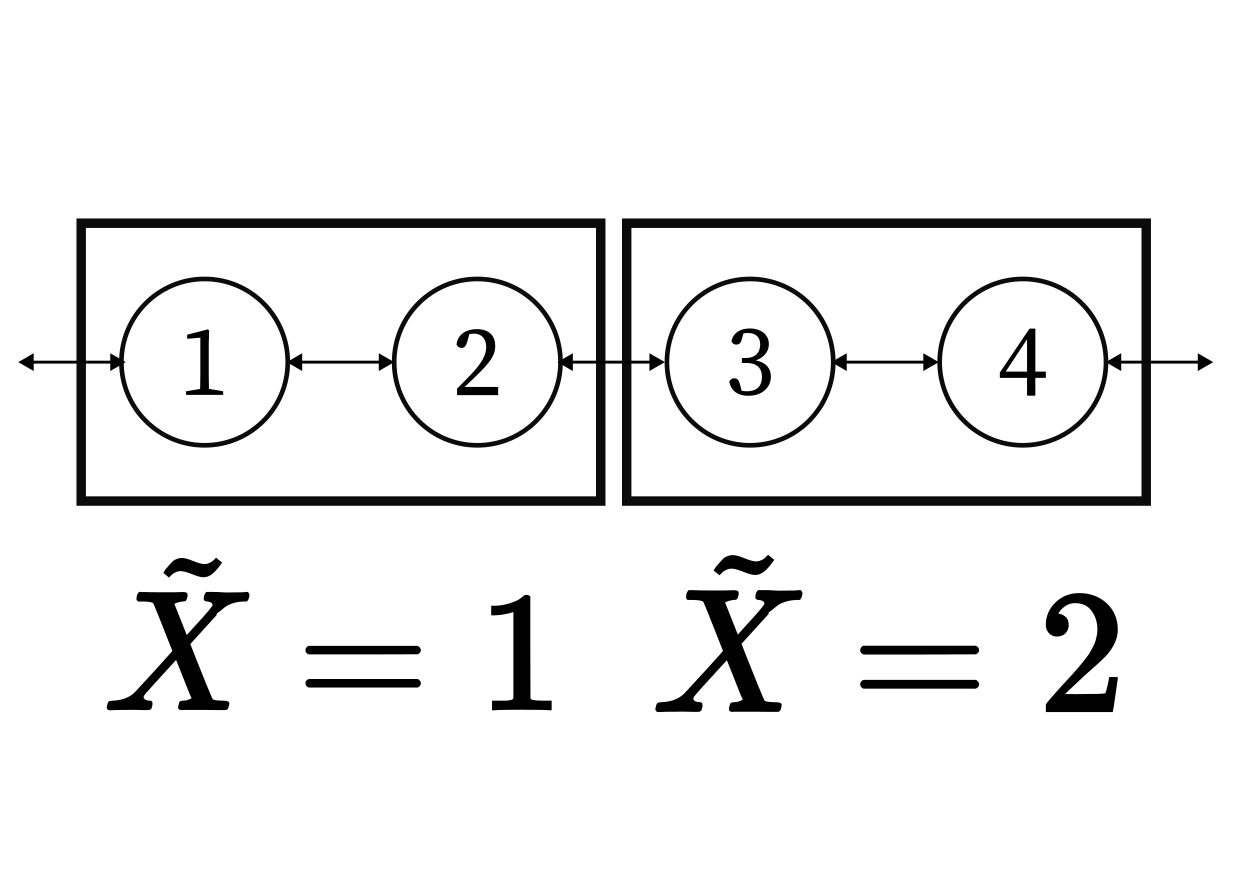
As discussed, this is non-Markov. In fact, for the appropriate construction, it is exactly 2nd order!

Results: Coarse-Grained Random Walk

h = h^{(2)}

Second order entropy equal to infinite order establishes this is a 2nd order process.

Results: Coarse-Grained Random Walk

h = h^{(2)}

Second order entropy equal to infinite order establishes this is a 2nd order process.

Correctly replicating theoretical entropy rates is an added bonus!

Results: Two Track Walk

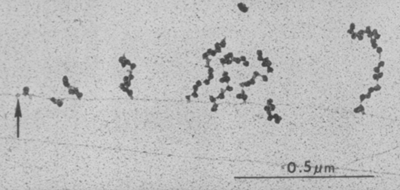
Sometimes, the RNA polymerase goes fast. Sometimes, it goes slow.

Miller OL Jr, Hamkalo BA, Thomas CA Jr. Visualization of bacterial genes in action. Science. 1970 Jul 24;169(3943):392-5. doi: 10.1126/science.169.3943.392. PMID: 4915822.

Results: Two Track Walk

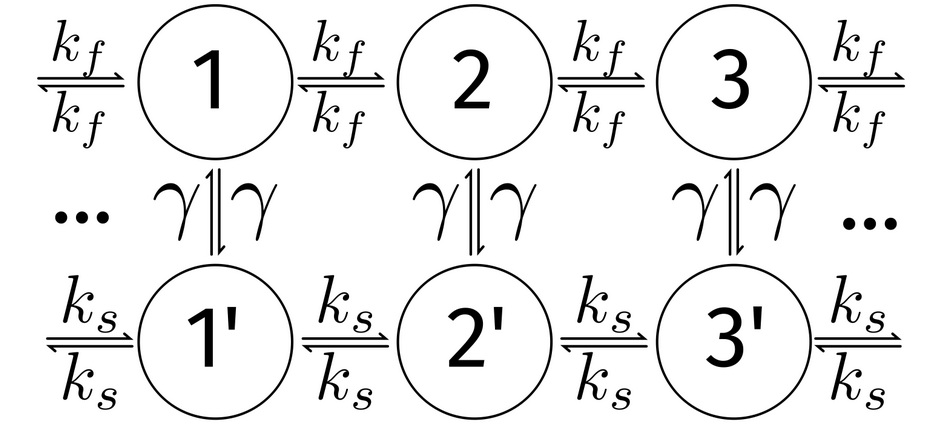
Fast

Slow

Abbondanzieri, Elio A., William J. Greenleaf, Joshua W. Shaevitz, Robert Landick, and Steven M. Block. 2005. “Direct Observation of Base-Pair Stepping by RNA Polymerase.” Nature 438 (7067): 460–65.

No theoretical results in most regimes of \( \gamma \).

In the limit of high \( \gamma \), should be a Markov process.

In the limit of low \( \gamma \), should recover a half-slow, half-fast walk.

Results: Two Track Walk

Results: Two Track Walk

Results: Two Track Walk

Lots more results!

See chapter 4 of the proposal for:
 

  • Additional model systems
  • Comparisons of different compression algorithms and how well the correction works across algorithms
  • Ablation studies on amount of available data
  • How inaccurate observation affects the method
  • Discussion of how representation of the process can affect the apparent Markov order

How can we extend this to a continuous-space, continuous-time process?

A Continuous Definition of Entropy

There exist continuous analogues of the entropy, e.g. the differential entropy, which is defined as

H(X) = -\int\limits_{x \in \mathcal{X}} p(x) \log p(x)

We can't compress something to negative infinity bits.

Would have to abandon many of the ideas of information theory, compression, etc.

Has some weird behaviors. For example, can go to negative infinity for a narrow Gaussian.

Discretization

Convert our continuous trajectory into a discrete one, and apply the discrete method to that.

Partition the space into disjoint regions and number them \(\{1 \dots N\}\).

Instead of describing the particle by its \((x, y)\) coordinates, describe it by a number that says which rectangle it's in.

Discretization

Convert our continuous trajectory into a discrete one, and apply the discrete method to that.

Partition the space into disjoint regions and number them \(\{1 \dots N\}\).

Instead of describing the particle by its \((x, y)\) coordinates, describe it by a number that says which rectangle it's in.

Known as "lumping"

Discretization by Lumping

Lumping introduces at least 2nd-order memory!

TIME

Milestone

Lump

A

B

C

D

1

2

3

A

Faradjian, Anton K., and Ron Elber. 2004. “Computing Time Scales from Reaction Coordinates by Milestoning.” The Journal of Chemical Physics 120 (23): 10880–89.

TIME

Milestone

Lump

A

B

C

D

1

2

3

A

B

1

Faradjian, Anton K., and Ron Elber. 2004. “Computing Time Scales from Reaction Coordinates by Milestoning.” The Journal of Chemical Physics 120 (23): 10880–89.

Faradjian, Anton K., and Ron Elber. 2004. “Computing Time Scales from Reaction Coordinates by Milestoning.” The Journal of Chemical Physics 120 (23): 10880–89.

TIME

Milestone

Lump

A

B

C

D

1

2

3

A

B

1

A

Faradjian, Anton K., and Ron Elber. 2004. “Computing Time Scales from Reaction Coordinates by Milestoning.” The Journal of Chemical Physics 120 (23): 10880–89.

TIME

Milestone

Lump

A

B

C

D

1

2

3

A

B

1

A

B

Faradjian, Anton K., and Ron Elber. 2004. “Computing Time Scales from Reaction Coordinates by Milestoning.” The Journal of Chemical Physics 120 (23): 10880–89.

TIME

Milestone

Lump

A

B

C

D

1

2

3

A

B

1

A

B

C

2

Faradjian, Anton K., and Ron Elber. 2004. “Computing Time Scales from Reaction Coordinates by Milestoning.” The Journal of Chemical Physics 120 (23): 10880–89.

TIME

Milestone

Lump

A

B

C

D

1

2

3

A

B

1

A

B

C

2

B

Faradjian, Anton K., and Ron Elber. 2004. “Computing Time Scales from Reaction Coordinates by Milestoning.” The Journal of Chemical Physics 120 (23): 10880–89.

TIME

Milestone

Lump

A

B

C

D

1

2

3

A

B

1

A

B

C

2

B

A

1

Faradjian, Anton K., and Ron Elber. 2004. “Computing Time Scales from Reaction Coordinates by Milestoning.” The Journal of Chemical Physics 120 (23): 10880–89.

TIME

Milestone

Lump

A

B

C

D

1

2

3

A

B

1

A

B

C

2

B

A

1

B

Faradjian, Anton K., and Ron Elber. 2004. “Computing Time Scales from Reaction Coordinates by Milestoning.” The Journal of Chemical Physics 120 (23): 10880–89.

TIME

Milestone

Lump

A

B

C

D

1

2

3

A

B

1

A

B

C

2

B

A

1

B

C

2

Faradjian, Anton K., and Ron Elber. 2004. “Computing Time Scales from Reaction Coordinates by Milestoning.” The Journal of Chemical Physics 120 (23): 10880–89.

TIME

Milestone

Lump

A

B

C

D

1

2

3

A

B

1

A

B

C

2

B

A

1

B

C

2

D

3

Faradjian, Anton K., and Ron Elber. 2004. “Computing Time Scales from Reaction Coordinates by Milestoning.” The Journal of Chemical Physics 120 (23): 10880–89.

TIME

Milestone

Lump

A

B

C

D

1

2

3

A

B

1

A

B

C

2

B

A

1

B

C

2

D

3

Faradjian, Anton K., and Ron Elber. 2004. “Computing Time Scales from Reaction Coordinates by Milestoning.” The Journal of Chemical Physics 120 (23): 10880–89.

Milestone

Lump

A

B

1

A

B

C

2

B

A

1

B

C

2

D

3

Milestone

Lump

A

B

1

A

B

C

2

B

A

1

B

C

2

D

3

By getting rid of repeated crossings between lumps, milestoning gets rid of second-order memory!

Can we use this to discretize our trajectories for analysis?

Milestoning A Markov Process

k
h^{(k)}
k
h^{(k)}

Expectation

Reality

Milestoning A Markov Process With Really Tiny Timesteps

k
h^{(k)}

Expectation

Reality

k
h^{(k)}

Apply tiny \(\delta t\)

In Search of Missed Crossings

Song, Kevin, Dmitrii E. Makarov, and Etienne Vouga. 2023. “The Effect of Time Resolution on the Observed First Passage Times in Diffusive Dynamics.” The Journal of Chemical Physics 158 (11): 111101.

Suppose I am watching a particle diffusing starting from a point \(x = x_0\) and want to know how long it takes the particle to first cross \(x = x_0 + L\).

x = x_0
x = x_0 + L

TIME

For a given time resolution \(\delta t\), how large can the error in this crossing time \( \Delta \) be?

Suppose I am watching a particle diffusing starting from a point \(x = x_0\) and want to know how long it takes the particle to first cross \(x = x_0 + L\).

x = x_0
x = x_0 + L

TIME

For a given time resolution \(\delta t\), how large can the error in this crossing time \( \Delta \) be?

Suppose I am watching a particle diffusing starting from a point \(x = x_0\) and want to know how long it takes the particle to first cross \(x = x_0 + L\).

x = x_0
x = x_0 + L

TIME

For a given time resolution \(\delta t\), how large can the error in this crossing time \( \Delta \) be?

Suppose I am watching a particle diffusing starting from a point \(x = x_0\) and want to know how long it takes the particle to first cross \(x = x_0 + L\).

x = x_0
x = x_0 + L

TIME

For a given time resolution \(\delta t\), how large can the error in this crossing time \( \Delta \) be?

Suppose I am watching a particle diffusing starting from a point \(x = x_0\) and want to know how long it takes the particle to first cross \(x = x_0 + L\).

x = x_0
x = x_0 + L

TIME

For a given time resolution \(\delta t\), how large can the error in this crossing time \( \Delta \) be?

Suppose I am watching a particle diffusing starting from a point \(x = x_0\) and want to know how long it takes the particle to first cross \(x = x_0 + L\).

x = x_0
x = x_0 + L

TIME

For a given time resolution \(\delta t\), how large can the error in this crossing time \( \Delta \) be?

Suppose I am watching a particle diffusing starting from a point \(x = x_0\) and want to know how long it takes the particle to first cross \(x = x_0 + L\).

x = x_0
x = x_0 + L

TIME

For a given time resolution \(\delta t\), how large can the error in this crossing time \( \Delta \) be?

Suppose I am watching a particle diffusing starting from a point \(x = x_0\) and want to know how long it takes the particle to first cross \(x = x_0 + L\).

x = x_0
x = x_0 + L

TIME

For a given time resolution \(\delta t\), how large can the error in this crossing time \( \Delta \) be?

Suppose I am watching a particle diffusing starting from a point \(x = x_0\) and want to know how long it takes the particle to first cross \(x = x_0 + L\).

For a given time resolution \(\delta t\), how large can the error in this crossing time \( \Delta \) be?

x = x_0
x = x_0 + L

TIME

Suppose I am watching a particle diffusing starting from a point \(x = x_0\) and want to know how long it takes the particle to first cross \(x = x_0 + L\).

x = x_0
x = x_0 + L

TIME

For a given time resolution \(\delta t\), how large can the error in this crossing time \( \Delta \) be?

Suppose I am watching a particle diffusing starting from a point \(x = x_0\) and want to know how long it takes the particle to first cross \(x = x_0 + L\).

x = x_0
x = x_0 + L

TIME

\Delta ?

For a given time resolution \(\delta t\), how large can the error in this crossing time \( \Delta \) be?

\(\Delta\) observed to be as large as \( 60 \delta t \)!

x = x_0
x = x_0 + L

TIME

\Delta

For a given time resolution \(\delta t\), how large can the error in this crossing time \( \Delta \) be?

A Corrective Algorithm

One does not simply get better data!

We can explicitly compute the probability that a crossing went unobserved in a timestep based on the positions at the end of each timestep, and reintroduce crossings in a probabilistic manner.

d_1
d_2
p_{\text{cross}}(x_1, x_2, \delta t) = \exp \left[ \frac{-d_1 d_2}{D \delta t} \right]

Results: Mean Exit Time

Estimated Mean Exit Time at \(\delta t = 0.01\)

True Mean Exit Time at \(\delta t = 0.01\)

Visualization of \(\delta t = 0.01\)

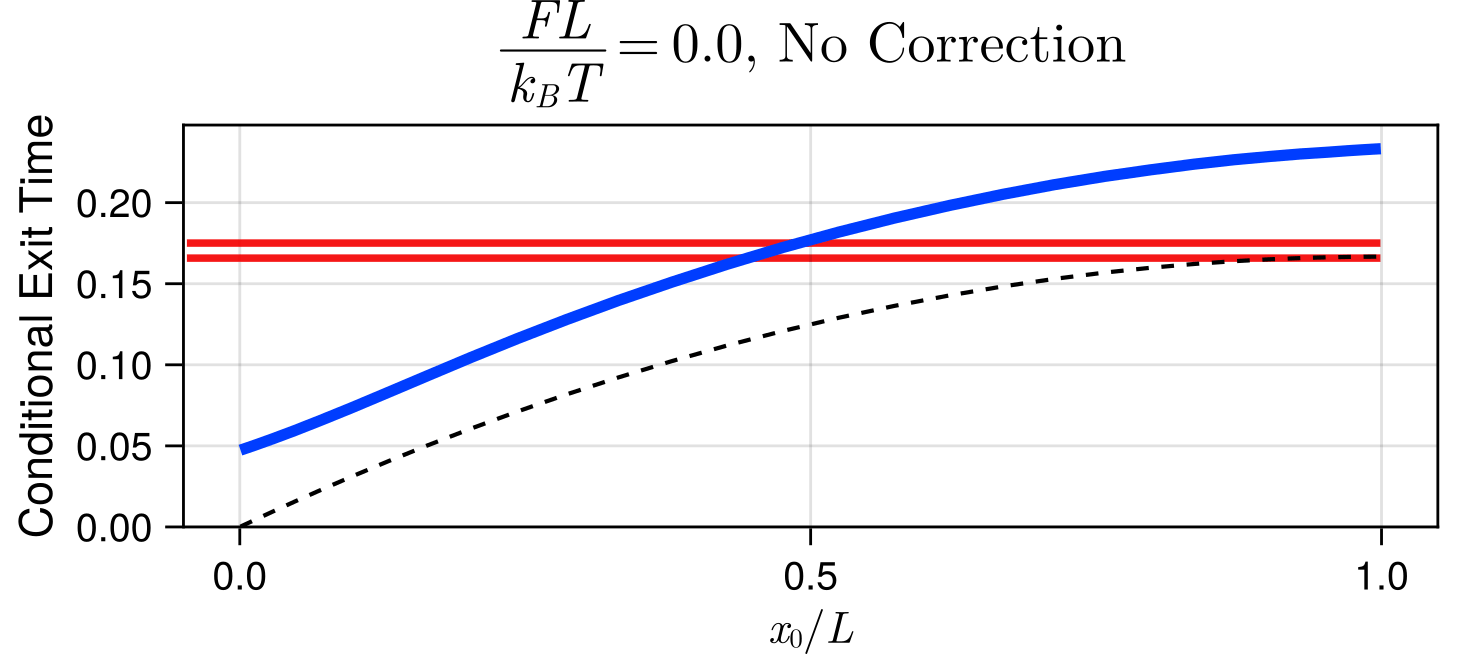
Results: Mean Exit Time

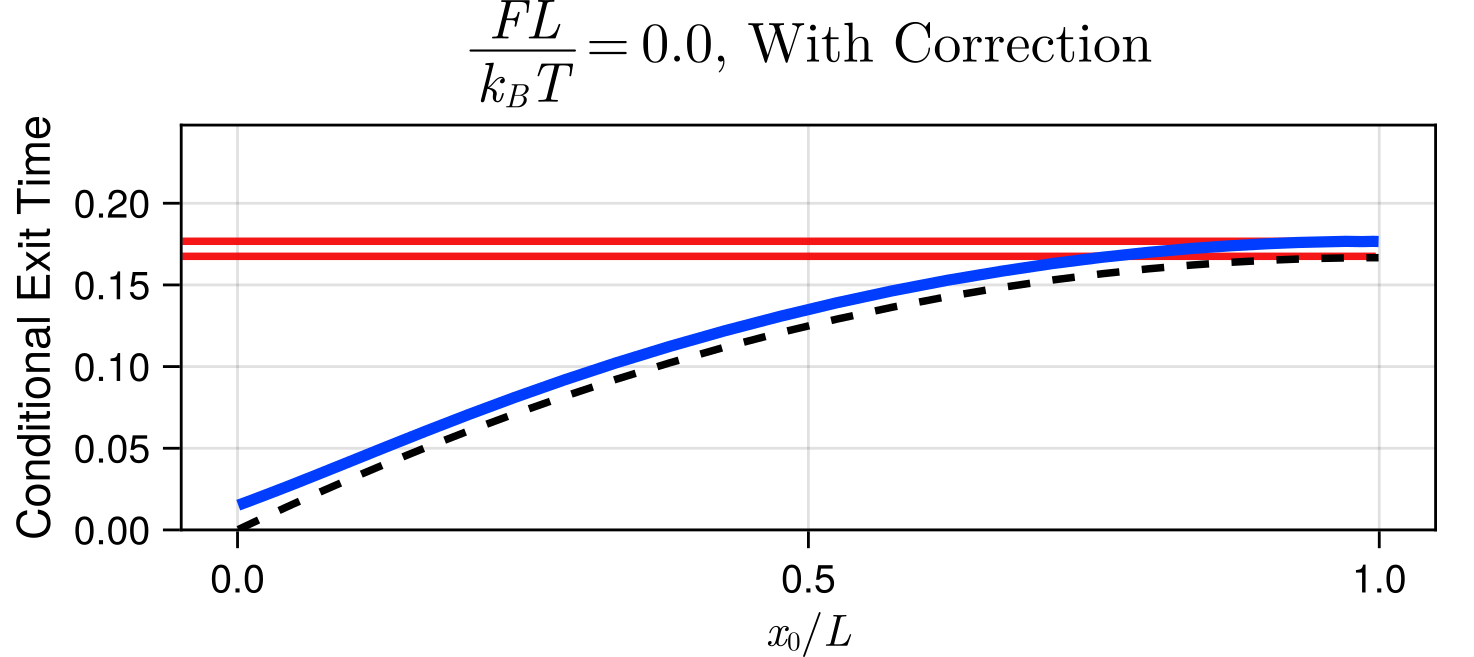
Estimated Mean Exit Time at \(\delta t = 0.01\)

True Mean Exit Time at \(\delta t = 0.01\)

Visualization of \(\delta t = 0.01\)

Applications on Real Continuous Systems

  1. Apply milestoning discretization
  2. Apply recrossing correction
  3. Apply discrete entropy rate estimator

Applications on Real Continuous Systems

  1. Apply milestoning discretization
  2. Apply recrossing correction
  3. Apply discrete entropy rate estimator

Applications on Real Continuous Systems

Song, Kevin, Raymond Park, Atanu Das, Dmitrii E. Makarov, and Etienne Vouga. 2023. “Non-Markov Models of Single-Molecule Dynamics from Information-Theoretical Analysis of Trajectories.” The Journal of Chemical Physics 159 (6). https://doi.org/10.1063/5.0158930.

Must account for two additional factors!

  1. Spacing of milestones is crucial for getting good results in a reasonable number of samples.
     
  2. In the continuous-time setting, the waiting time between milestone transitions can introduce non-Markov behavior into the system.

Discussed in Chapter 6

Results: Gly-Ser Repeat Peptide

Diffusive Simulation, Compression

Diffusive Simulation, Plug-in

Gly-Ser Simulation, Compression

Gly-Ser Simulation, Plug-in

Lots More Results!

See Chapter 5 of the proposal for:

  • How to apply the method when the diffusion coefficient \(D\) is not known a priori
  • Results on the splitting probability of diffusion in an interval
  • Results of application of this technique to a non-Markov systems

See Chapter 6 of the proposal for:

  • Theoretical analysis of how change in waiting time distributions affect the entropy rate of the discretized process
  • How to extract the energy dissipation of a driven system from estimates of the entropy rate.
  • Comparisons of our method against other continuous-time, continuous-space Markovianity detection criteria like the Chapman-Kolmogorov equations.
  • Even more model systems!

Chapter 5: Missed Crossing Correction

Chapter 6: Continuous Markovanity Detection

Milestoning and Entropy Production

Is this thing alive?

Q: What does it mean for something to be alive?

A: This is a can of worms that I refuse to touch.

Q: How can you tell if something is alive if you refuse to define what it means to be alive?

A: For the purposes of this section, we'll say something is alive if its actions are not time reversible.

This does have the unfortunate side effect of making things like fires and powerplants alive. ¯\_(ツ)_/¯

Entropy Production

It has long been understood that irreversible processes increase the entropy of the universe ("generate entropy").

It was not until recently that this was linked to statements about microscopic trajectories.

Crooks, G. E. 1999. “Entropy Production Fluctuation Theorem and the Nonequilibrium Work Relation for Free Energy Differences.” Physical Review. E, Statistical Physics, Plasmas, Fluids, and Related Interdisciplinary Topics 60 (3): 2721–26.

Entropy Production

\langle \dot{S} \rangle = k_B T \cdot D_{KL}( X_t \;\|\; \theta(X_t))

Average change in entropy over time, averaged over the trajectory

Entropy Production

\langle \dot{S} \rangle = k_B T \cdot D_{KL}( X_t \;\|\; \theta(X_t))

Average change in entropy over time, averaged over the trajectory

Kullback-Leibler Divergence

D_{KL}(X \;\|\; Y) = \sum_{z} p_X(z) \log\left[ \frac{p_X(z)}{p_Y(z)} \right]

Entropy Production

\langle \dot{S} \rangle = k_B T \cdot D_{KL}( X_t \;\|\; \theta(X_t))

Average change in entropy over time, averaged over the trajectory

Kullback-Leibler Divergence

Time-reversed version of \(X_t\)

D_{KL}(X \;\|\; Y) = \sum_{z} p_X(z) \log\left[ \frac{p_X(z)}{p_Y(z)} \right]
D_{KL}(X \;\|\; Y) = \sum_{z} p_X(z) \log\left[ \frac{p_X(z)}{p_Y(z)} \right]

👀

H(X) = -\sum\limits_{z} p(z) \log p(z)

Do the same sorts of problems with estimating entropy rate (inadequate spatial/temporal resolution, issues with coarse-graining) come into play when estimating entropy production?

Yes.

Can we solve these problems with milestoning?

Yes, but...

Milestoning comes with its own problems.

Recall: A milestone crossing is marked the first time we reach that milestone, but not on subsequent recrossings.

3

2

1

TIME

1

2

3

Forward Milestone

Milestoning comes with its own problems...

Recall: A milestone crossing is marked the first time we reach that milestone, but not on subsequent recrossings.

3

2

1

TIME

1

2

3

Milestone

Reverse-then-Milestone

1

2

3

Different waiting times will result in different entropy production!

Kinetic Hysteresis

Unknown how to solve kinetic hysteresis problem!

  • Some works stick to situations in which intermilestone times are always short, so the problem doesn't pop up.
     
  • Some works disregard intermilestone times when carrying out the analysis.
    • Recent work demonstrates that in some cases, one must throw out intermilestone times.
    • Can't always do this: can construct cases where intermilestone times must not be ignored!
       
  • Room for something else?

Hartich, David, and Aljaž Godec. 2023. “Violation of Local Detailed Balance upon Lumping despite a Clear Timescale Separation.” Physical Review Research 5 (3): L032017.

Hartich, David, and Aljaž Godec. 2021. “Emergent Memory and Kinetic Hysteresis in Strongly Driven Networks.” Physical Review X 11 (4): 041047.

Summary + Proposed Work

Markovianity Detection + Entropy Rate Estimation

  • With the appropriate care taken to deal with slow convergence, and to choose the right representations, compression algorithms can detect non-Markov behavior in a wide range of physical systems.
     
  • Gives us the first unified framework for how to think about memory effects in both discrete and continuous systems.

Milestoning: Where do we stand?

  • Milestoning and its variants can improve inference for incomplete dynamics for both entropy rate and entropy production estimation.
     
  • Requires some care in its use due to potential for missed crossings.
     
  • Suffers from kinetic hysteresis when used as a representation for entropy production.
d_1
d_2

Still many unknowns about the capabilities of milestoning

  • Can this technique be extended to multiple spatial dimensions for entropy rate estimation and Markovianity detection?
  • Why do we need to discard wait times in some cases, but not in others? Is there some principle that tells us when we need to discard wait times?
  • Is the effect of kinetic hysteresis inherent to the technique of milestoning, or is there some way to avoid it?

Still many unknowns about the capabilities of milestoning

  • Can this technique be extended to multiple spatial dimensions for entropy rate estimation and Markovianity detection?
  • Why do we need to discard wait times in some cases, but not in others? Is there some principle that tells us when we need to discard wait times?
  • Is the effect of kinetic hysteresis inherent to the technique of milestoning, or is there some way to avoid it?

Proposed Work

Can this technique be extended to multiple spatial dimensions for entropy rate estimation and Markovianity detection?

Run experiments to determine whether interface-based milestoning is viable for entropy rate estimation in two-dimensional, continuous-time systems.

Estimated completion: July 2024

Proposed Work

Is the effect of kinetic hysteresis inherent to the technique of milestoning, or is there some way to avoid it?

Run experiments to assess the viability of midpoint milestoning, a new proposed milestoning technique which assigns the midpoint of the first and last crossings to the time of the state change in a milestone, in computing the entropy production of a stochastic process.

 

Midpoint milestoning is impossible to compute without some amount fine-grained information, but there may exist relaxations which remove kinetic hysteresis while still being computable.

Estimated completion: October 2024

1

2

3

FIN

Extra Slides

h^{(8)}(\{X_i\}) = \sum_{x_i \in \mathcal{X}} p(x_1 \dots x_9) \log p(x_9 | x_1, x_2, x_3, x_4, \dots, x_8)
= \sum_{x_i \in \mathcal{X}} p(x_1 \dots x_9) \log p(x_9 | x_4 \dots x_8)
= \sum_{x_i \in \mathcal{X}} p(x_4 \dots x_9) \log p(x_9 | x_4 \dots x_8)
= h^{(5)}(\{X_i\})

In general, if \(X_i\) is a \(k\)-th order Markov process, then

h^{(k+a)} = h^{(k)}

Discretizing Continuous Trajectories

Convert our continuous trajectory into a discrete one, and apply the discrete method to that.

Badly-chosen discretization scheme can introduce memory effects---not good if we're trying to assess whether a system has memory.

Incomplete information typically introduces memory effects!

Key Assumption: Stationarity

Unless otherwise stated, we assume that all processes in this talk are stationary.

A stochastic process is stationary iff for all \(x_i \in \mathcal{X}\) and all \( t_i, \ell \in \mathcal{T} \):

p(X_{t_1} = x_1, X_{t_2} = x_2, \dots, X_{t_n} = x_n )
= p(X_{t_1 + \ell} = x_1, X_{t_2 + \ell} = x_2, \dots, X_{t_n + \ell} = x_n )

If I wait some amount of time, the process's behavior does not change.

Conditioning Decreases Entropy

\sum_{i=1}^n a_i \lg \left( \frac{a_i}{b_i} \right) \geq \left( \sum_{i=1}^n a_i \right) \lg \left( \frac{\sum_{i=1}^n a_i}{\sum_{i=1}^n b_i} \right) = a \lg \frac{a}{b}
H(X | Y) = -\sum_{x,y} p(x, y) \lg \left[ \frac{p(x , y)}{p(y)} \right]
=-\sum_{x} \left[ \sum_y p(x,y) \lg \left( \frac{ p(x,y) }{ p(y) } \right) \right]
\geq -\sum_{x} \left[ \left(\sum_y p(x,y)\right) \lg \left( \frac{ \sum_y p(x,y) }{ \sum_y p(y) } \right) \right]
= -\sum_x p(x) \lg p(x) = H(X)

High-\(k\) Limit of Conditional Entropy Achieves Entropy Rate

PRNGs and Kolmogorov Complexity

Most PRNGs generate deterministic sequences---they are deterministic 1-Markov processes, so their entropy is zero. They also have low Kolmogorov complexity, since their minimal generating program is a copy of the PRNG + the initial RNG seed.

The analysis presented in this talk clearly cannot correctly predict that the output of a PRNG is Markov, nor can it detect that a sequence of PRNG-generated numbers has low Kolmogorov complexity.

The applications we are interested in are where  

Terminology Table

k = 1 1 < k < ∞ unbounded
Markov ✅ ❌ ❌
k-Markov ✅ (k = 1) ✅ ❌
Finite Order ✅ ✅ ❌
Infinite order ❌ ❌ ✅

(Lowest) Markov Order

Name

We will use \(k\) as our definition of memory in a stochastic process.

h^{(k+1)} \leq h^{(k)}

for all \(k\)

Conditioning Decreases Entropy

H(X_n | X_{n-1}, X_{n-2}, \dots, X_{n-k-1})
\leq H(X_n | X_{n-1}, X_{n-2}, \dots, X_{n-k})

High-\(k\) Limit

In the limit as \( k \to \infty \)

\lim_{k \to \infty} h^{(k)}(\{X_i\}) = h(\{X_i\})
p(X_i = x_i | X_{i-1} = x_{i-1}, X_{i-2} = x_{i-2}, \dots, X_1 = x_1) = p(X_i = x_i | X_{i-1} = x_{i-1})

Conditional Entropy for Markov Process

h^{(2)} = H(X_3 | X_2, X_1)
= \sum_{x_1, x_2, x_3 \in \mathcal{X}} p(x_3, x_2, x_1) \log p(x_3| x_2, x_1)
= \sum_{x_1, x_2, x_3 \in \mathcal{X}} p(x_3, x_2, x_1) \log p(x_3| x_2)
= \sum_{x_2, x_3 \in \mathcal{X}} p(x_3, x_2) \log p(x_3| x_2)
= H(X_3 | X_2) = h^{(1)}

Backup Plot

A Corrective Algorithm

Suppose we have a discrete walk of \(n\) steps on a 1D lattice, and two endpoints that are \(s_1\) and \(s_2\) steps from some endpoint. What fraction of possible walks cross the endpoint?

s_1
s_2

TIME

\(n\) (not to scale)

A Corrective Algorithm

s_1
s_2

\(n\)

Suppose that we have \(\ell\) steps that go left and \(r\) steps that go right in this walk.

Then we have

n = \ell + r
s_1 - s_2 = \ell - r
n_{s_1, s_2} = {n \choose \ell} = {n \choose \frac{n + s_1 - s_2}{2}}
\ell = \frac{n + s_1 - s_2}{2}

How many of these walks cross our endpoint?

A Corrective Algorithm

s_1
s_2
n_{s_1, s_2} = {n \choose \ell} = {n \choose \frac{n + s_1 - s_2}{2}}

How many of these walks cross our endpoint?

s_2

A Corrective Algorithm

s_1
s_2

How many of these walks cross our endpoint?

s_2
n_{s_1, s_2} = {n \choose \ell} = {n \choose \frac{n + s_1 - s_2}{2}}

A Corrective Algorithm

s_1
s_2

How many walks go from \(s_1\) to \(-s_2\)?

s_2
n = \ell' + r'
s_1 + s_2 = \ell' - r'
\ell' = \frac{n + s_1 + s_2}{2}
n_{s_1, s_2}^{\text{cross}} = {n \choose \ell'} = {n \choose \frac{n + s_2 + s_1}{2}}
n_{s_1, s_2} = {n \choose \ell} = {n \choose \frac{n + s_1 - s_2}{2}}

A Corrective Algorithm

n_{s_1, s_2} = {n \choose r} = {n \choose \frac{n + s_2 - s_1}{2}}

How many walks go from \(s_1\) to \(-s_2\)?

n_{s_1, s_2}^{\text{cross}} = {n \choose \ell'} = {n \choose \frac{n + s_2 + s_1}{2}}
p^{\text{cross}}_{s_1, s_2} =

A Corrective Algorithm

n_{s_1, s_2} = {n \choose r} = {n \choose \frac{n + s_2 - s_1}{2}}
n_{s_1, s_2}^{\text{cross}} = {n \choose \ell'} = {n \choose \frac{n + s_2 + s_1}{2}}
p^{\text{cross}}_{s_1, s_2} =

This is a non-physical formula! There is no concept of distance, time, or how fast the particle can move.

Need to:

  • Turn \(s_1\) and \(s_2\) into physical distances
  • Express \(n\) as a function of time and particle mobility \(D\)
  • Place a \(\delta x\) on the grid.
\log p^{\text{cross}}_{x_1, x_2} = \log
\binom{\frac{2D\delta{t}}{\Delta x^2}}{\frac{D\delta t}{\Delta x^2} + \frac{x_2 - x_1}{2 \Delta x}}
\binom{\frac{2D\delta{t}}{\Delta x^2}}{\frac{D\delta t}{\Delta x^2} + \frac{x_2 + x_1}{2 \Delta x}}

2. Use Stirling's Approximation

3.Lots of Algebra

p^{\text{cross}}_{x_1, x_2} = \exp\left[ \frac{-x_1 x_2}{D \delta{t}} \right]

Add crossings back in with this probability at every timestep!

1. Take limit as \(\Delta x \to 0\)

Tackling The Continuous Setting

Song, Kevin, Raymond Park, Atanu Das, Dmitrii E. Makarov, and Etienne Vouga. 2023. “Non-Markov Models of Single-Molecule Dynamics from Information-Theoretical Analysis of Trajectories.” The Journal of Chemical Physics 159 (6). https://doi.org/10.1063/5.0158930.

To analyze continuous trajectories

  1. Apply milestoning discretization
  2. Apply missed crossing correction of previous section
  3. Apply discrete entropy rate estimators

To analyze continuous trajectories

  1. Apply milestoning discretization
  2. Apply missed crossing correction of previous section
  3. Apply discrete entropy rate estimators

Two additional wrinkles!

1. On sufficiently small length scales, all motion looks diffusive!

2. In the continuous-time setting, we have to worry about the contribution of waiting times to non-Markov behavior.

Two additional wrinkles!

2. In the continuous-time scenario, we have to worry about the contribution of waiting times to non-Markov behavior.

1. On sufficiently small length scales, all motion looks diffusive!

On sufficiently small length scales, all motion looks diffusive!

On sufficiently small length scales, all motion looks diffusive!

In order to properly capture non-Markov behavior, need to have milestones that are far apart

In order to properly capture non-Markov behavior, need to have milestones that are far apart

This requires large timesteps to achieve---high probability of missing crossings unless corrective technique is applied.

Results: Glycine-Serine Repeat Fragment

Diffusive Simulation, Compression

Diffusive Simulation, Plug-in

Gly-Ser Simulation, Compression

Gly-Ser Simulation, Plug-in

Lots more results!

See Chapter 6 of the proposal for:

  • Theoretical analysis of how change in waiting time distributions affect the entropy rate of the discretized process
  • How to extract the energy dissipation of a driven system from estimates of the entropy rate.
  • Comparisons of our method against other continuous-time, continuous-space Markovianity detection criteria like the Chapman-Kolmogorov equations.
  • Even more model systems!

State of the Art

(prior to last Thursday)

In 2023, Hartich and Godec showed that milestoning trajectories using states instead of interfaces can lead to improved estimates of entropy production.

Hartich, David, and Aljaž Godec. 2023. “Violation of Local Detailed Balance upon Lumping despite a Clear Timescale Separation.” Physical Review Research 5 (3): L032017.

Dwell time outside of milestone states must be short relative to time within milestones.

State of the Art

(prior to last Thursday)

In 2023, Hartich and Godec showed that milestoning trajectories using states instead of interfaces can lead to improved estimates of entropy production.

Hartich, David, and Aljaž Godec. 2023. “Violation of Local Detailed Balance upon Lumping despite a Clear Timescale Separation.” Physical Review Research 5 (3): L032017.

Dwell time outside of milestone states must be short relative to time within milestones.

State of the Art

(prior to last Thursday)

In 2023, Hartich and Godec showed that milestoning trajectories using states instead of interfaces can lead to improved estimates of entropy production.

Hartich, David, and Aljaž Godec. 2023. “Violation of Local Detailed Balance upon Lumping despite a Clear Timescale Separation.” Physical Review Research 5 (3): L032017.

Dwell time outside of milestone states must be short relative to time within milestones.

State of the Art

(prior to last Thursday)

In 2023, Hartich and Godec showed that milestoning trajectories using states instead of interfaces can lead to improved estimates of entropy production.

Hartich, David, and Aljaž Godec. 2023. “Violation of Local Detailed Balance upon Lumping despite a Clear Timescale Separation.” Physical Review Research 5 (3): L032017.

Dwell time outside of milestone states must be short relative to time within milestones.

State of the Art

(prior to last Thursday)

In 2023, Hartich and Godec showed that milestoning trajectories using states instead of interfaces can lead to improved estimates of entropy production.

Hartich, David, and Aljaž Godec. 2023. “Violation of Local Detailed Balance upon Lumping despite a Clear Timescale Separation.” Physical Review Research 5 (3): L032017.

Dwell time outside of milestone states must be short relative to time within milestones.

State of the Art

(since last Thursday)

Blom, Kristian, Kevin Song, Etienne Vouga, Aljaž Godec, and Dmitrii E. Makarov. 2023. “Milestoning Estimators of Dissipation in Systems Observed at a Coarse Resolution: When Ignorance Is Truly Bliss.” arXiv [cond-Mat.stat-Mech]. arXiv. http://arxiv.org/abs/2310.06833. Accepted for publication at PNAS.

It is possible to construct systems where the waiting times must be discarded to accurately compute the entropy production!

Somewhat puzzling: there are other examples of systems where waiting times must not be discarded to accurately compute the entropy production.

Construct a case in which milestoning can correctly recover the entropy production without needing intermilestone times to be short.