Protein-Protein Docking

with F2Dock and ZDock

Author: Kevin Song, material from Bajaj (UT) and Liwang (UC Merced)

What is a Protein?

What is the Protein Docking Problem?

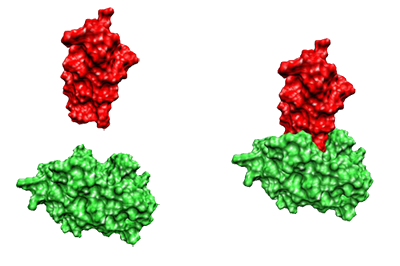
Given two proteins, find the optimal pose (positioning) that maximizes bonding interactions

Factors to Consider

Properties of a good dock
 

  • Surfaces close together
     
  • Opposite charged atoms close together
     
  • Hydrophobic surfaces hidden

Properties of a bad dock
 

  • Proteins tunneling into each other
     
  • Same charges close together

Goal: Given two protein structures, optimize docking

If proteins were rigid bodies, this problem would be (relatively) easy! Unfortunately, life is complicated...

Meet Hemoglobin!

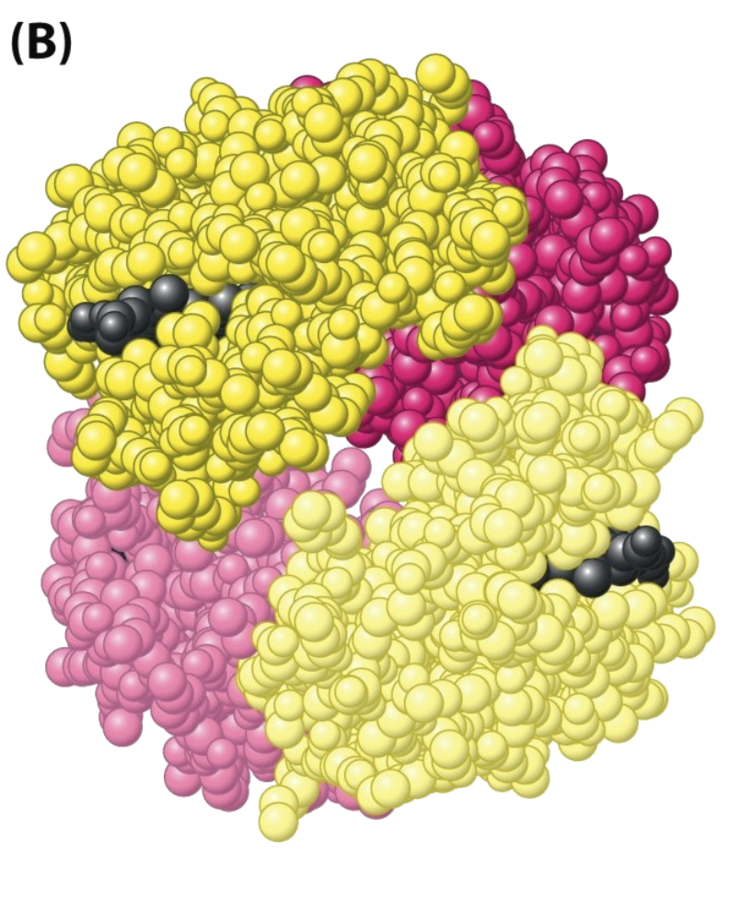
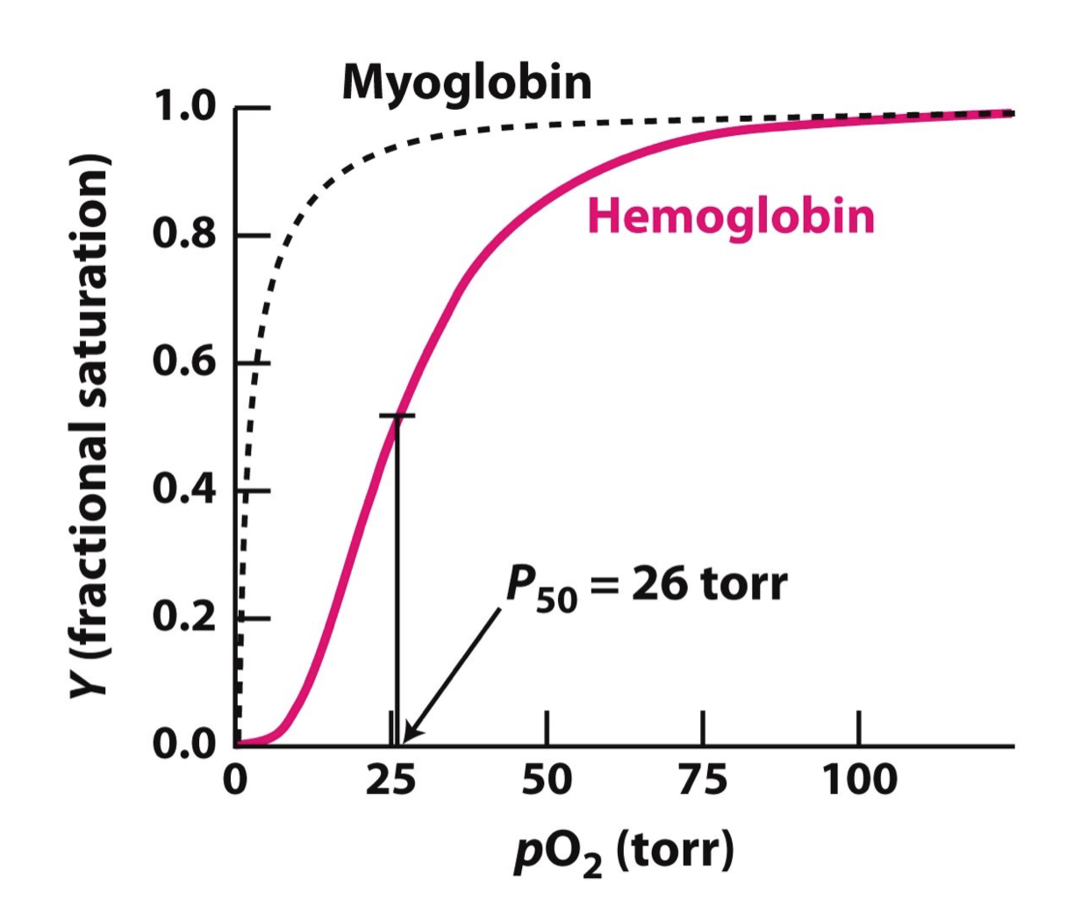
Images from Berg,Tymoczko,Stryer, 8th ed.

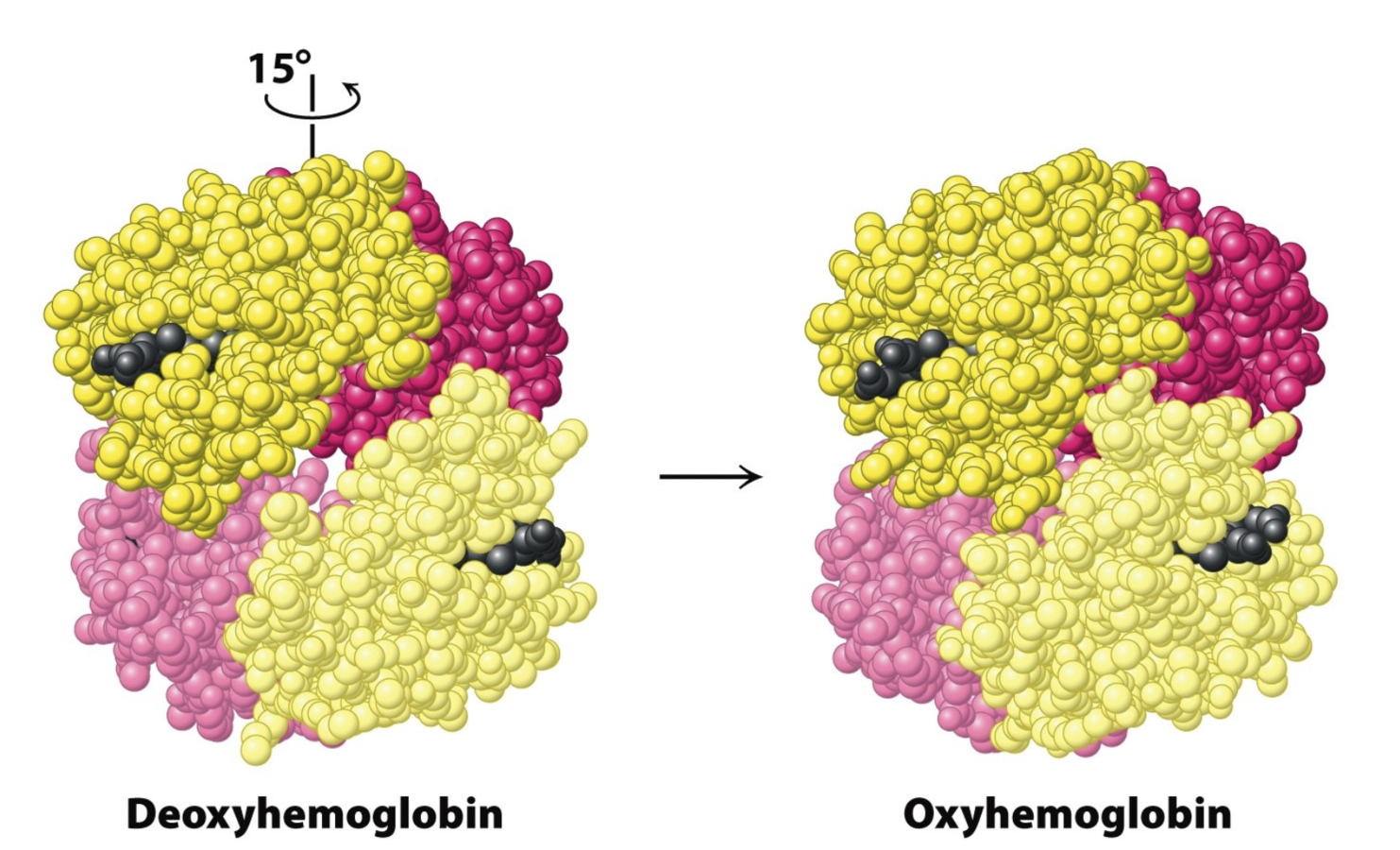
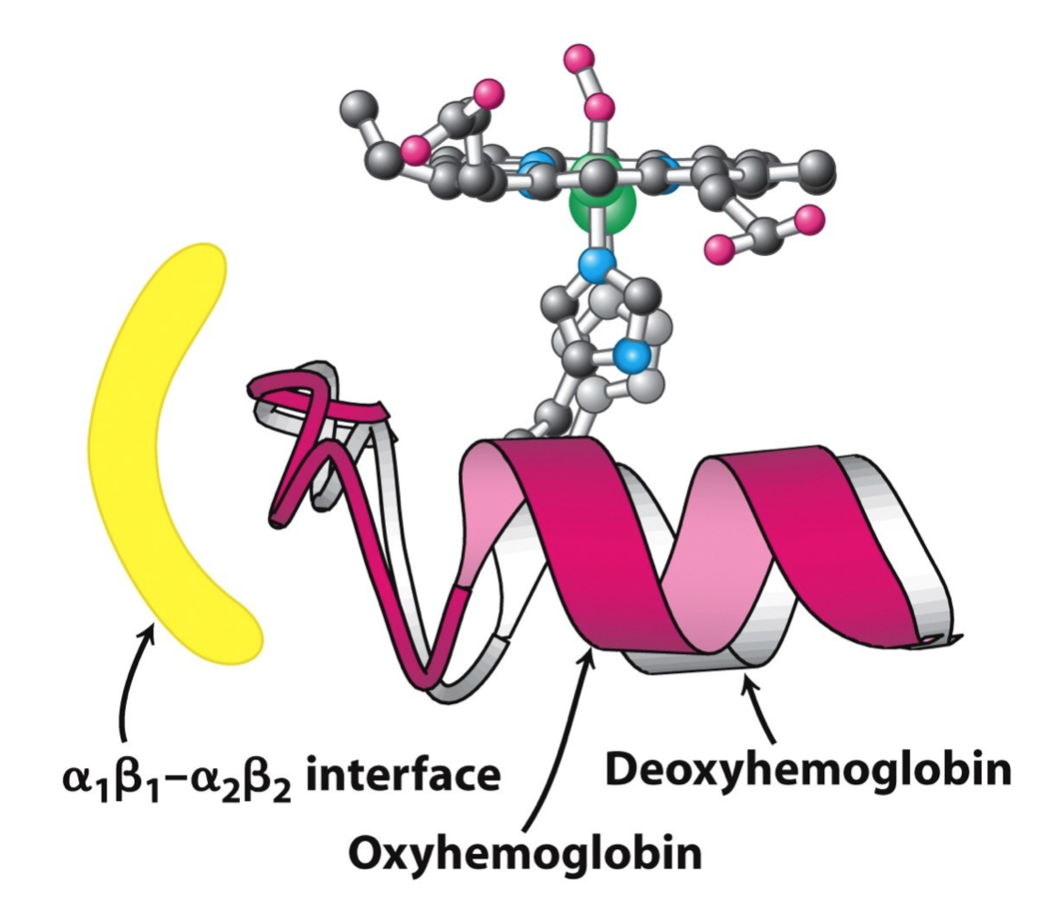
Oxygen binding in deoxyhemoglobin stimulates conformational change. Oxyhemoglobin has better affinity to oxygen.

Images from Berg,Tymoczko,Stryer, 8th ed.

Other Factors at Play

  • 2,3-bisphosphoglycerate in
    quaternary binding pocket
  • Amino acids in α2γ2 subunit affect
    oxygen affinity
  • Protonation of residues (Bohr Effect)
  • Additional effects (not well understood)

Protein Binding is complicated!

Simulation Techniques

Molecular Dynamics

  • Use physics (force fields and energy) to calculate molecular motions
  • Can incorporate elements of Monte Carlo simulations (randomness)
  • Is the gold standard for most protein problems

Literally Everything Else

Soft Optimization Methods

Principal Idea: We can't compute all conformational changes that occur upon binding.

Instead, find some objective functions that tolerate a little bit of mismatch, and hope that this allows us to find docking sites.

Problem Statement

Given two molecules    and    , and an affinity function    , find all rotations     and translations      such that:

A
AA
B
BB
f
ff
\Delta_r
Δr\Delta_r
T_t
TtT_t
\displaystyle{ \int\limits_x w_r \text{Re} [f_A(x) \cdot T_t( \Delta_r (f_B(x))] }
∫xwrRe[fA(x)⋅Tt(Δr(fB(x))]\displaystyle{ \int\limits_x w_r \text{Re} [f_A(x) \cdot T_t( \Delta_r (f_B(x))] }
- w_i \text{Im} [f_A(x) \cdot T_t( \Delta_r (f_B(x))] dx \geq \tau
−wiIm[fA(x)⋅Tt(Δr(fB(x))]dx≥τ- w_i \text{Im} [f_A(x) \cdot T_t( \Delta_r (f_B(x))] dx \geq \tau
\tau
τ\tau

where     is a user-defined threshold and       and       are weights

w_r
wrw_r
w_i
wiw_i

Affinity Functions

Define an Affinity Function associated with a molecule       to be a function from           

For any two proteins A and B, the docking score) can be evaluated by the following integral:

\mathbb{R}^3 \rightarrow \mathbb{C}
R3→C\mathbb{R}^3 \rightarrow \mathbb{C}
\text{Score} = G \left({\displaystyle \int\limits_{\mathbb{R}^3} } f_A(x)f_B(x) \, dx\right)
Score=G(∫R3fA(x)fB(x)dx)\text{Score} = G \left({\displaystyle \int\limits_{\mathbb{R}^3} } f_A(x)f_B(x) \, dx\right)
A
AA

Example Molecules

A

B

\text{Score} = Re \left[ \sum\limits_x f_A(x)f_B(x) \right] - Im \left[ \sum\limits_x f_A(x)f_B(x) \right]
Score=Re[∑xfA(x)fB(x)]−Im[∑xfA(x)fB(x)]\text{Score} = Re \left[ \sum\limits_x f_A(x)f_B(x) \right] - Im \left[ \sum\limits_x f_A(x)f_B(x) \right]
f_A(x)
fA(x)f_A(x)
f_B(x)
fB(x)f_B(x)
\text{Score} = Re \left[ \sum\limits_x f_A(x)f_B(x) \right] - Im \left[ \sum\limits_x f_A(x)f_B(x) \right]
Score=Re[∑xfA(x)fB(x)]−Im[∑xfA(x)fB(x)]\text{Score} = Re \left[ \sum\limits_x f_A(x)f_B(x) \right] - Im \left[ \sum\limits_x f_A(x)f_B(x) \right]
\text{Score} = 4 - 81 - [4 \cdot18] = -149
Score=4−81−[4⋅18]=−149\text{Score} = 4 - 81 - [4 \cdot18] = -149

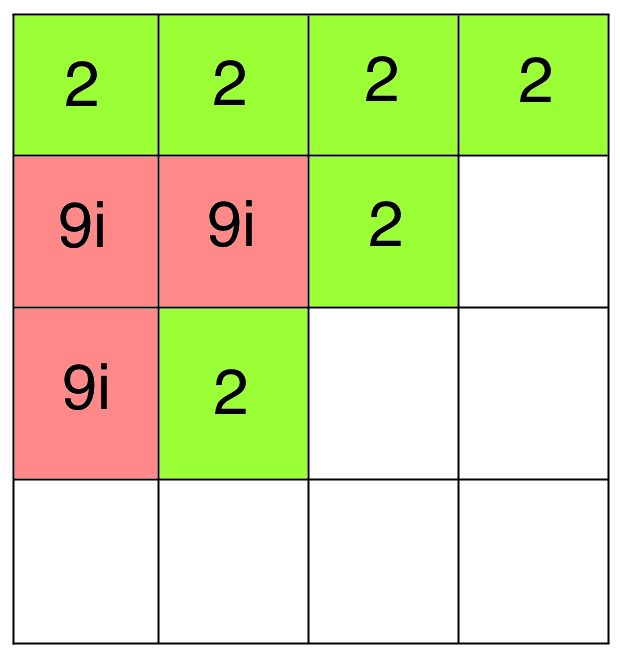
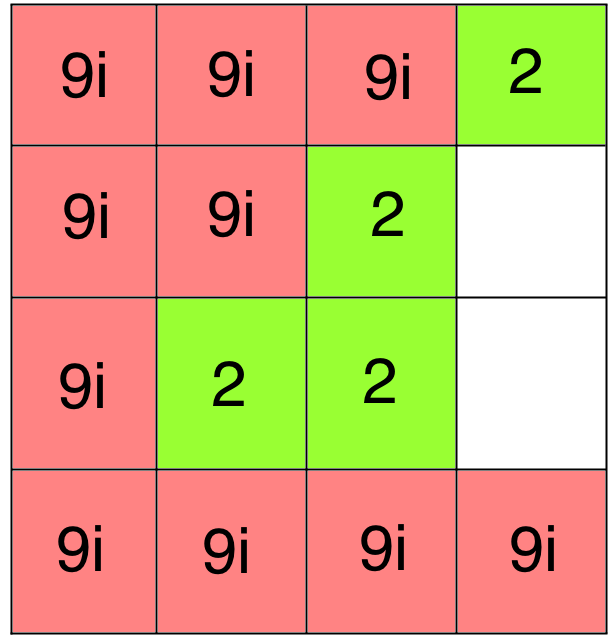
Bad Docking!

\text{Score} = Re \left[ \sum\limits_x f_A(x)f_B(x) \right] - Im \left[ \sum\limits_x f_A(x)f_B(x) \right]
Score=Re[∑xfA(x)fB(x)]−Im[∑xfA(x)fB(x)]\text{Score} = Re \left[ \sum\limits_x f_A(x)f_B(x) \right] - Im \left[ \sum\limits_x f_A(x)f_B(x) \right]
f_A(x)
fA(x)f_A(x)
\Delta_{180}(f_B(x))
Δ180(fB(x))\Delta_{180}(f_B(x))
\text{Score} = Re \left[ \sum\limits_x f_A(x)f_B(x) \right] - Im \left[ \sum\limits_x f_A(x)f_B(x) \right]
Score=Re[∑xfA(x)fB(x)]−Im[∑xfA(x)fB(x)]\text{Score} = Re \left[ \sum\limits_x f_A(x)f_B(x) \right] - Im \left[ \sum\limits_x f_A(x)f_B(x) \right]
\text{Score} = 4\cdot 2 = 8
Score=4⋅2=8\text{Score} = 4\cdot 2 = 8

Good Docking!

Problem Statement

Given two molecules    and    , and an affinity function    , find all rotations     and translations      such that:

A
AA
B
BB
f
ff
\Delta_r
Δr\Delta_r
T_t
TtT_t
\displaystyle{ \int\limits_x w_r \text{Re} [f_A(x) \cdot T_t( \Delta_r (f_B(x))] }
∫xwrRe[fA(x)⋅Tt(Δr(fB(x))]\displaystyle{ \int\limits_x w_r \text{Re} [f_A(x) \cdot T_t( \Delta_r (f_B(x))] }
- w_i \text{Im} [f_A(x) \cdot T_t( \Delta_r (f_B(x))] dx \geq \tau
−wiIm[fA(x)⋅Tt(Δr(fB(x))]dx≥τ- w_i \text{Im} [f_A(x) \cdot T_t( \Delta_r (f_B(x))] dx \geq \tau
\tau
τ\tau

where     is a user-defined threshold and       and       are weights

w_r
wrw_r
w_i
wiw_i

Real Affinity Functions

Shape Complementarity

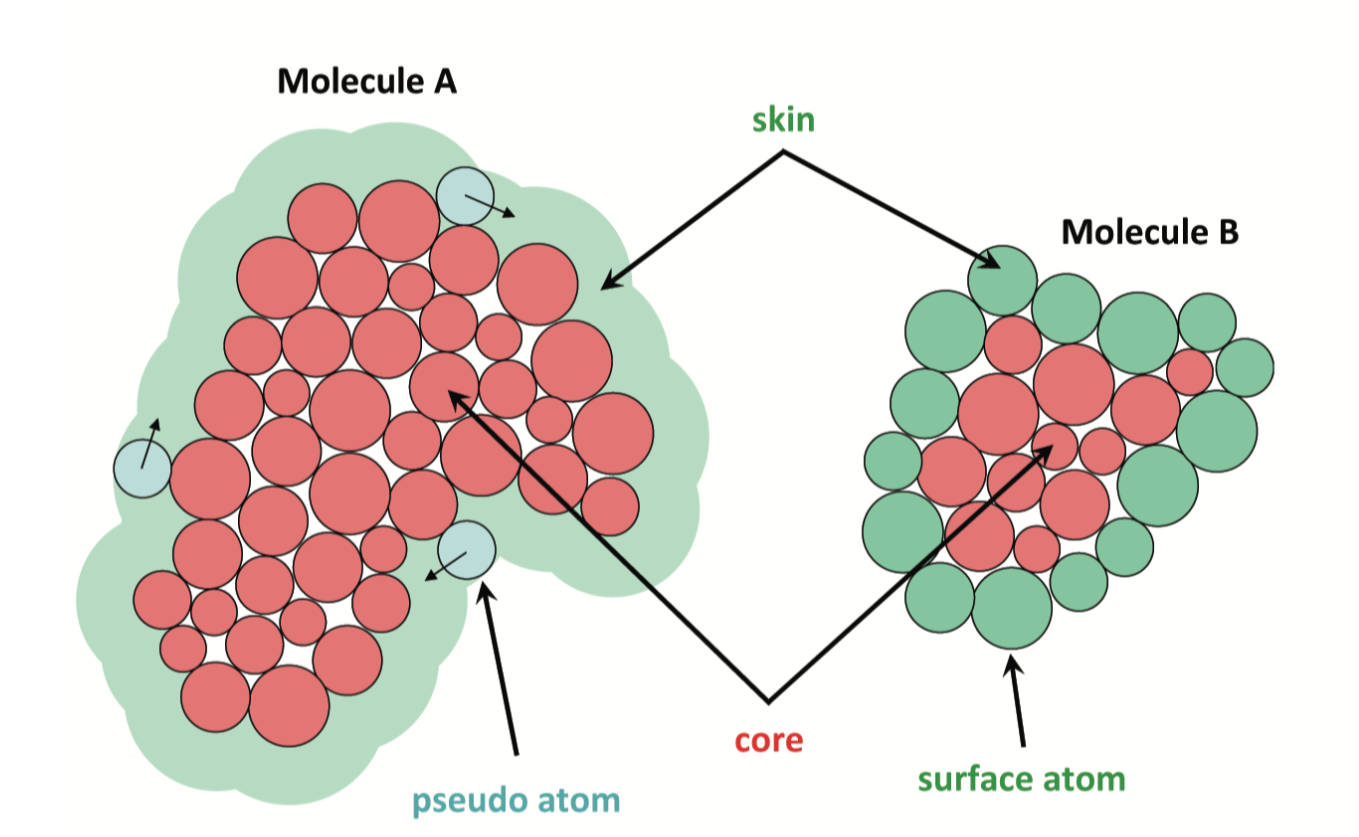
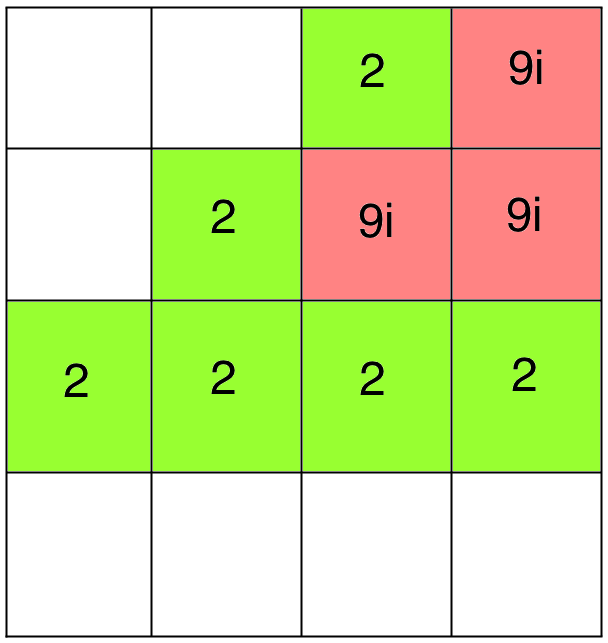
For Receptor: Positive weights in grown-skin layer, imaginary weights in core.

For Ligand: Positive weights in surface layer, imaginary weights in core.

Real Affinity Functions

Electrostatics

f_E^A(x) = \sum\limits_{k=1}^{M_A} q_k \frac{1}{(x-x_k)\,\epsilon(x-x_k)}
fEA(x)=∑k=1MAqk1(x−xk)ϵ(x−xk)f_E^A(x) = \sum\limits_{k=1}^{M_A} q_k \frac{1}{(x-x_k)\,\epsilon(x-x_k)}
f_E^B(x) = \sum\limits_{j=1}^{M_B} q_j \delta(x-x_j)
fEB(x)=∑j=1MBqjδ(x−xj)f_E^B(x) = \sum\limits_{j=1}^{M_B} q_j \delta(x-x_j)
\displaystyle{ \int f_A^E(x)f_B^E(x) \,dx = \sum\limits_{j=1}^{M_A}\sum\limits_{k=1}^{M_B} \frac{1}{\epsilon(x_j - x_k)}\frac{q_j q_k}{(x_j - x_k)} }
∫fAE(x)fBE(x)dx=∑j=1MA∑k=1MB1ϵ(xj−xk)qjqk(xj−xk)\displaystyle{ \int f_A^E(x)f_B^E(x) \,dx = \sum\limits_{j=1}^{M_A}\sum\limits_{k=1}^{M_B} \frac{1}{\epsilon(x_j - x_k)}\frac{q_j q_k}{(x_j - x_k)} }

Coulombic Potential Energy

So how do we actually find the best configurations?

Naïve Method

For every possible translation and rotation, evaluate the integral (or summation) of affinity functions.

 

In a 3D grid with N intervals, it takes        time to evaluate the summation once.

 

There are       possible translations.

 

With      rotations, this is a search time of

N^3
N3N^3
N^3
N3N^3
R
RR
\Omega \left( N^3 \cdot N^3 \cdot R \right) = \Omega\left(N^6 R \right)
Ω(N3⋅N3⋅R)=Ω(N6R)\Omega \left( N^3 \cdot N^3 \cdot R \right) = \Omega\left(N^6 R \right)

Look at 1D Case

Want to find the offset     such that the overlap integral is maximized:

y
yy
\displaystyle{ \max_y \; g(y) = \int f_1(x) \cdot f_2(x - y) dx }
maxyg(y)=∫f1(x)⋅f2(x−y)dx\displaystyle{ \max_y \; g(y) = \int f_1(x) \cdot f_2(x - y) dx }

This integral is a cross-correlation!

Look at 1D Case

The Fourier Convolution theorem allows us to express the convolution as a product of its Fourier Transforms!

\displaystyle{ FT\left(\int f_1(x) \cdot f_2(x - y)\, dx\right) = FT(f_1(x)) \cdot FT(f_2(x)) }
FT(∫f1(x)⋅f2(x−y)dx)=FT(f1(x))⋅FT(f2(x))\displaystyle{ FT\left(\int f_1(x) \cdot f_2(x - y)\, dx\right) = FT(f_1(x)) \cdot FT(f_2(x)) }

Naïve 1D Convolution

1D Fourier Convolution

\Theta(N^2)
Θ(N2)\Theta(N^2)
\Theta(N \lg N)
Θ(NlgN)\Theta(N \lg N)

Use FFT to solve 3D

We can convolve the affinity functions along the translations and perform an inverse peak search to rapidly identify translations for which the score is above the threshold!

\text{Score}_{SC}(x',y',z') = IFT(FFT(f_A) \cdot FFT(f_B))
ScoreSC(x′,y′,z′)=IFT(FFT(fA)⋅FFT(fB))\text{Score}_{SC}(x',y',z') = IFT(FFT(f_A) \cdot FFT(f_B))

Convolution with FFT in 3D

3D FFT

\Theta(N^3 \lg N)
Θ(N3lgN)\Theta(N^3 \lg N)

Peak Search

\Theta(N^3)
Θ(N3)\Theta(N^3)

Total Runtime

\Theta(R N^3 \lg N)
Θ(RN3lgN)\Theta(R N^3 \lg N)

Much better!

ZDock

ZDock is an older protein-docking software suite that was developed at BU

Grid-based affinity functions:

  • Shape Complementarity (GSC)
  • Desolvation Energy (ACE)
  • Electrostatics (CHARMM19)

Later versions replaced GSC with a better shape-complementarity function (PSC) and added faster FFT routines.


Pierce BG, et. al.  (2014) ZDOCK Server: Interactive Docking Prediction of Protein-Protein Complexes and Symmetric Multimers.

ZDock PSC


Pierce BG, et. al.  (2014) ZDOCK Server: Interactive Docking Prediction of Protein-Protein Complexes and Symmetric Multimers.

An affinity function based off of number of nearby atoms on the other protein.

 

In a naive setting, much slower to compute than traditional grown-skin shape-complementarity functions.

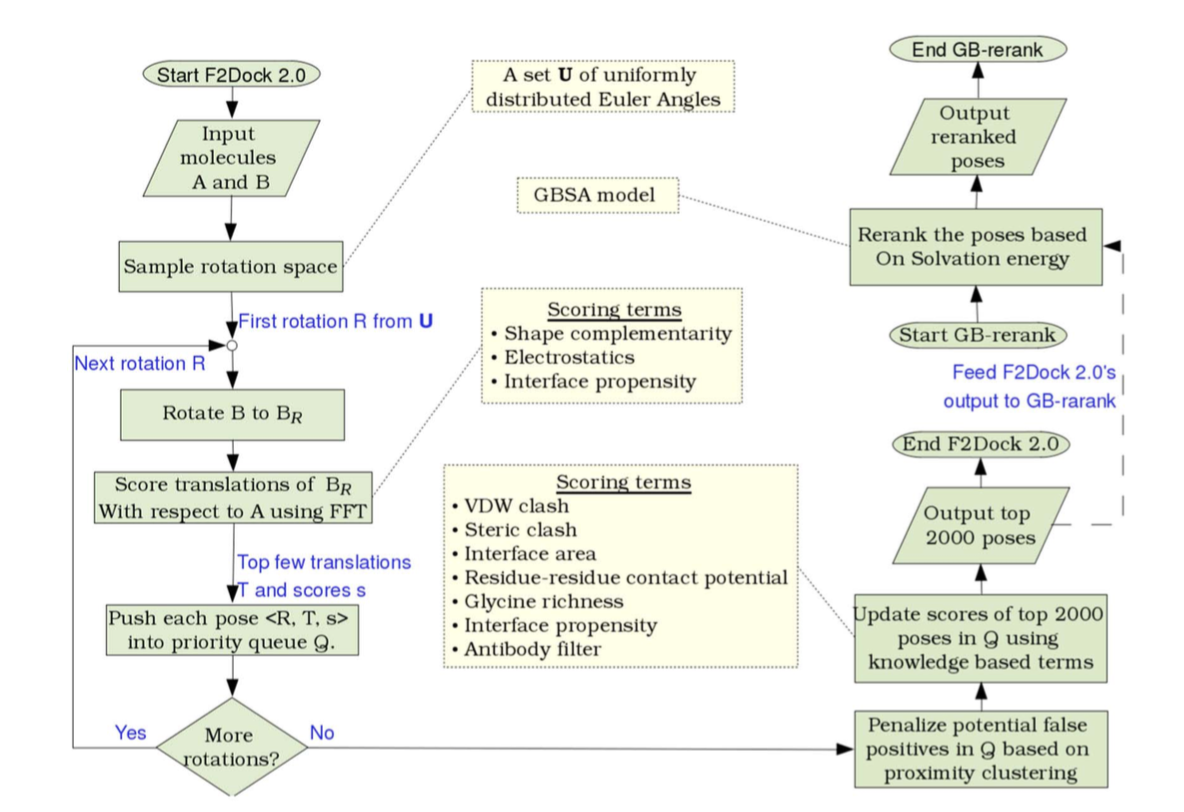
F2Dock

A relatively recent soft docking suite developed by CVC @ UT.

Saves time and memory by using NFFT (nonequispaced FFT) and exploiting sparsity in the inputs and outputs.

C. Bajaj, R. Chowdhury, and V. Siddavanahalli F2Dock: Fast Fourier Protein-Protein Docking

Only uses SC and Electrostatic AF!

F2Dock

After initial ranking, cluster poses and rerank with Generalized Born solvation energies

C. Bajaj, R. Chowdhury, and V. Siddavanahalli F2Dock: Fast Fourier Protein-Protein Docking

FIN