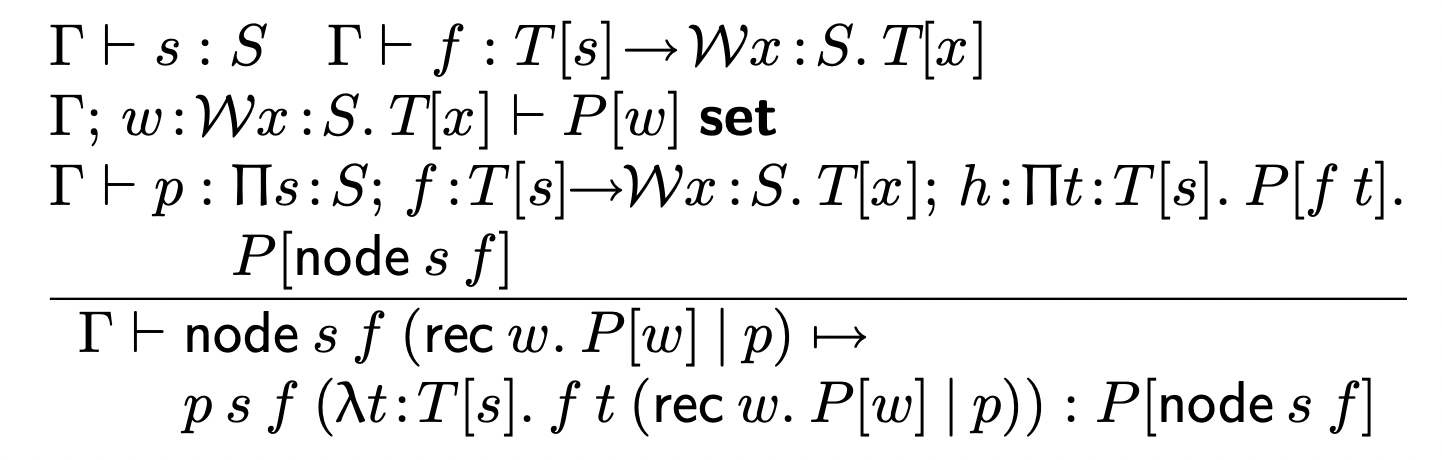ACTS Mar 13
W types
How is it used in Observational Type Theory? Someone's future talk
Help with code and syntax - I have pseudocode!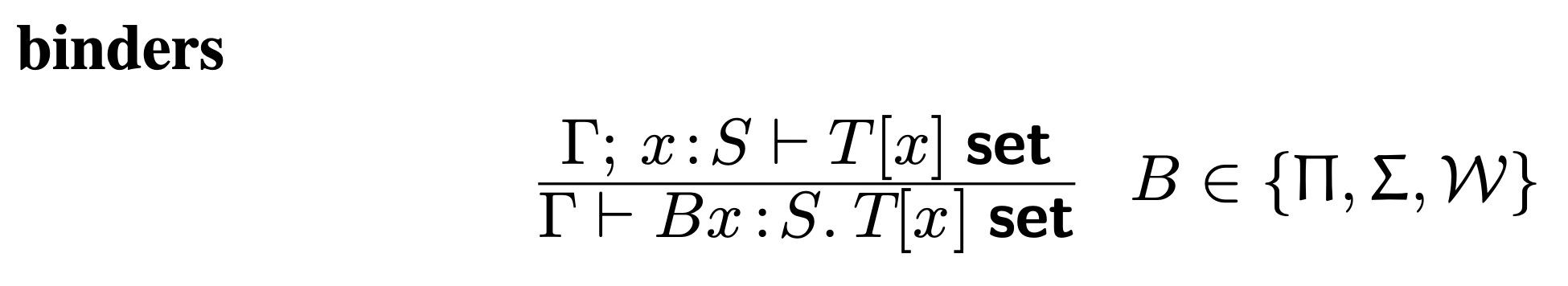
Formation
S: Type of the label of node
T[x]: Arity of child of node
Nat := W[
S := {ZeroLabel, SuccLabel} ,
f := {
ZeroLabel => Empty
SuccLabel => Unit
}
]
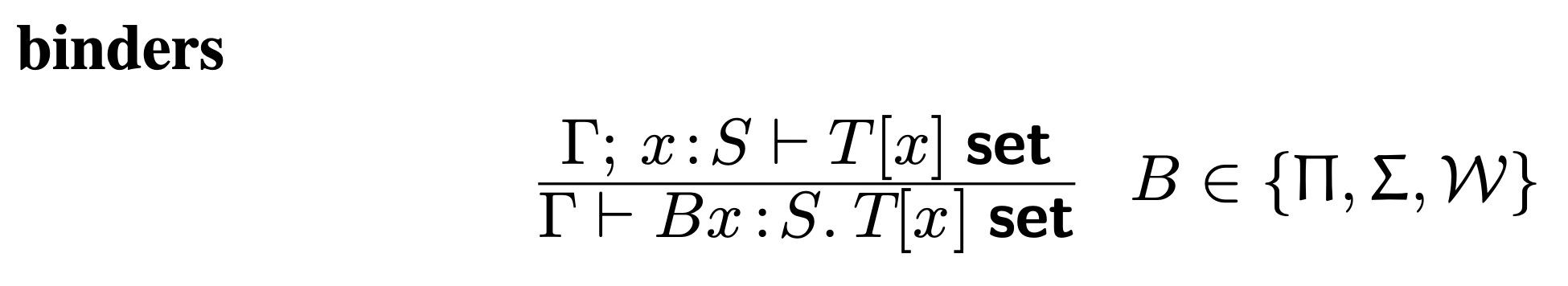
Pseudocode incoming
BTree := W[
S := {LeafLabel, TwoChildLabel},
f := {
ZeroLabel => Empty
TwoChildLabel => Bool
}
]
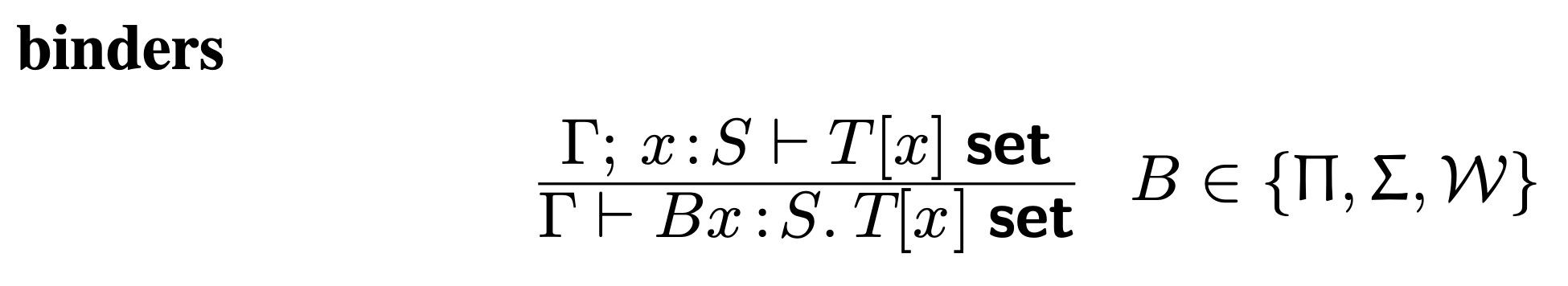
Introduction
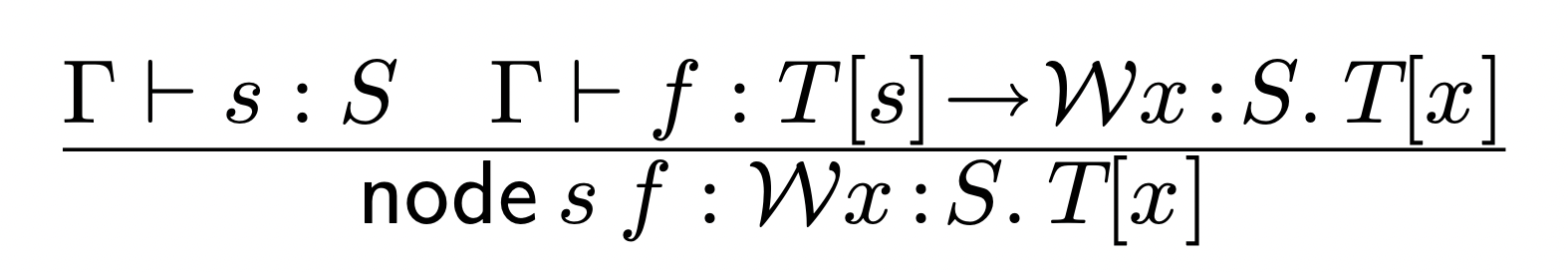
A node is created from a label and all its children
zero() := node (
s := ZeroLabel,
f := Empty.elim)
succ (n: Nat) := node (
s := SuccLabel,
f := () => n
)
Creating a Nat
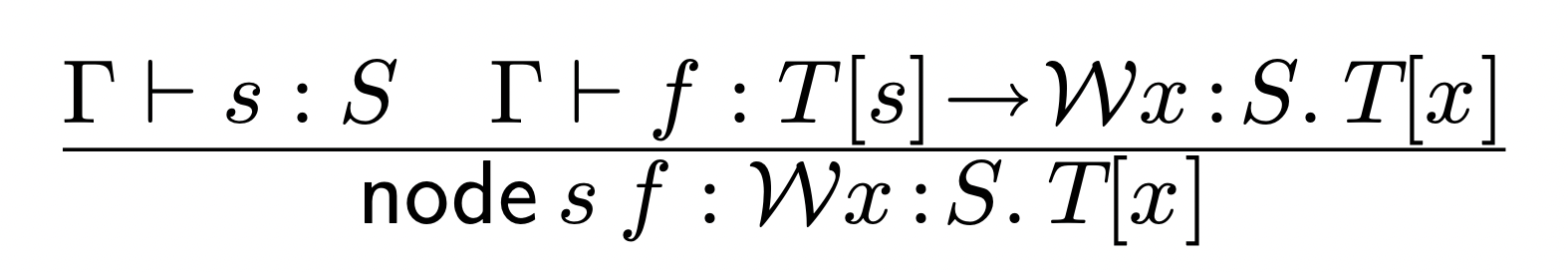
leaf() := node (
s := LeafLabel,
f := Empty.elim)
bt_node (l: BTree, r: BTree) := node (
s := TwoChildLabel,
f := { tt => l
ff => r}
)
Creating a BTree
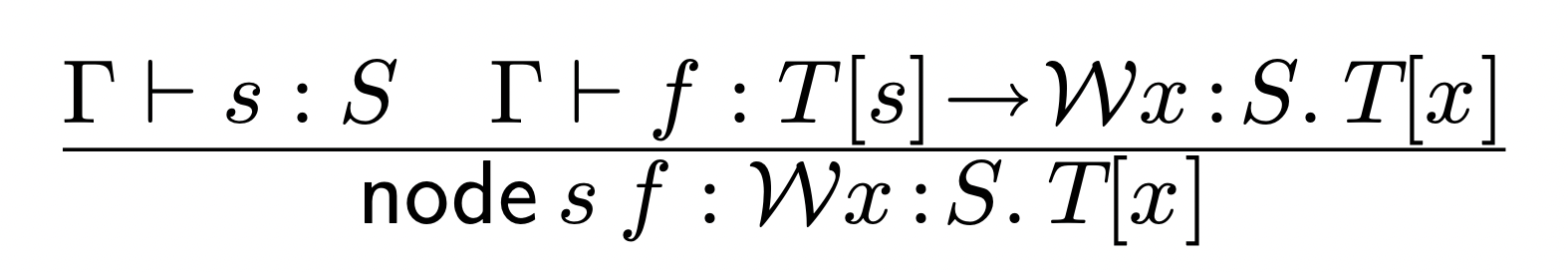
Elimination
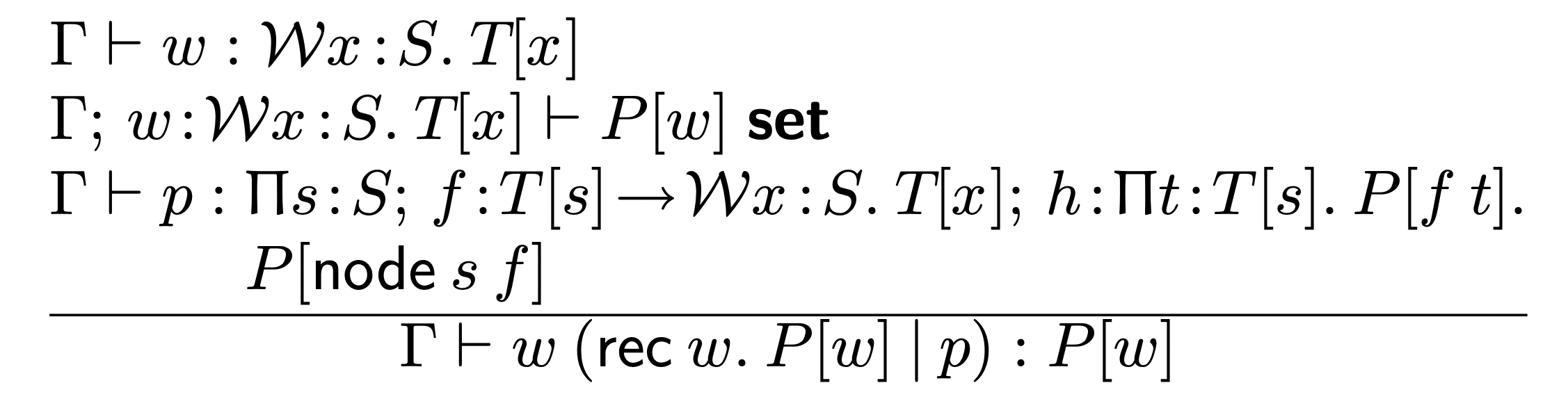
You can prove a conclusion for an arbitrary W-type if for any label, proving something for any child implies proving something for the node with that label and child.
indNat
(n: Nat)
(P: Nat -> Type)
(base: P zero)
(inductive_hyp: (n: Nat) -> P n -> P (succ n)) : P n
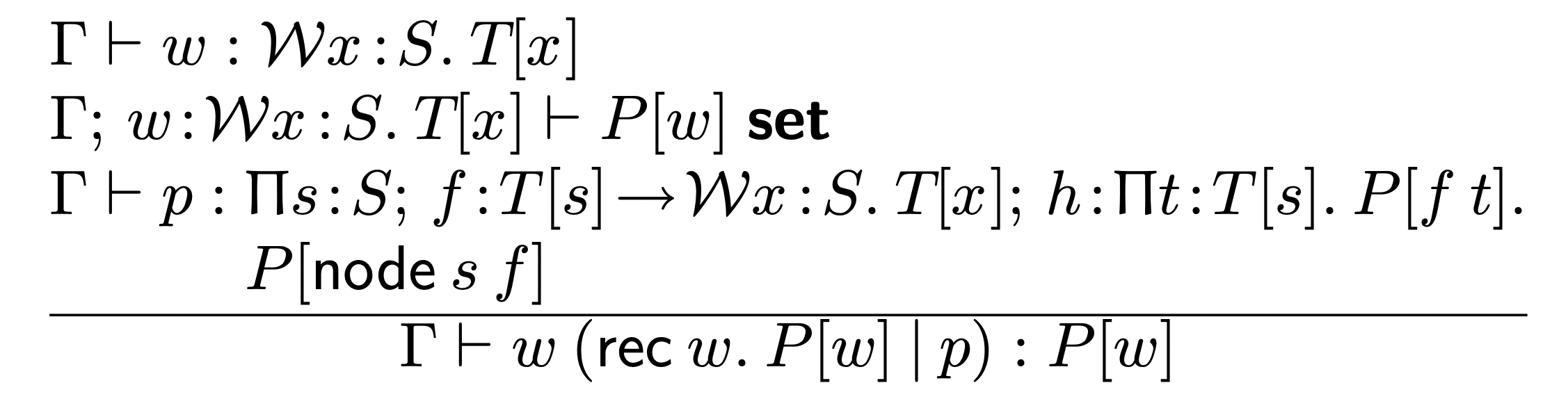
indBTree
(bt: BTree)
(P: BTree -> Type)
(leaf_p: P leaf)
(bt_node_p: (l: BTree, r: BTree) -> (P l, P r) -> P (bt_node l r)): P bt
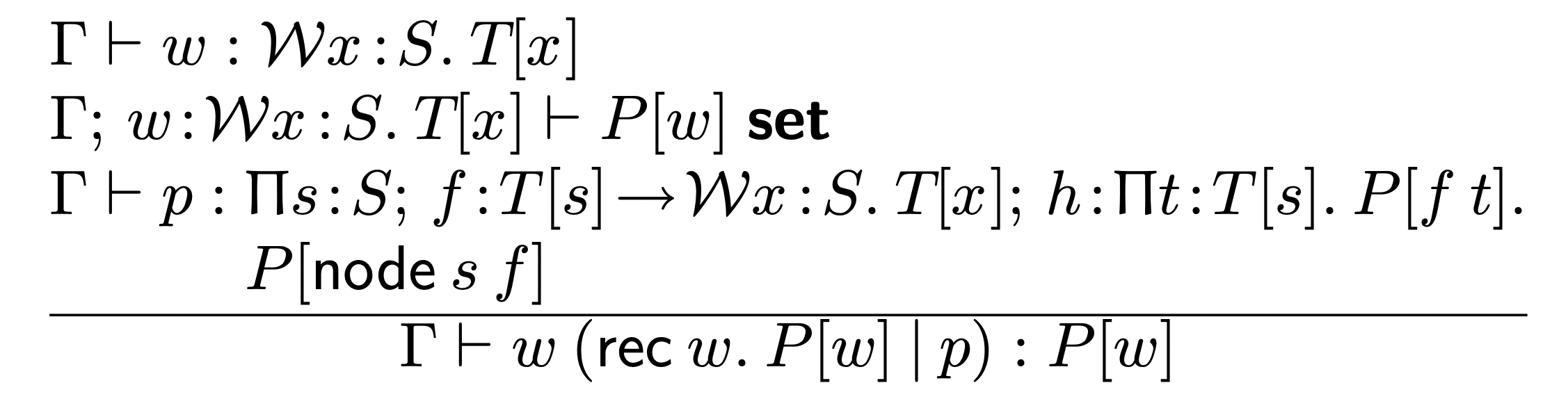
Computation/"Conversion"
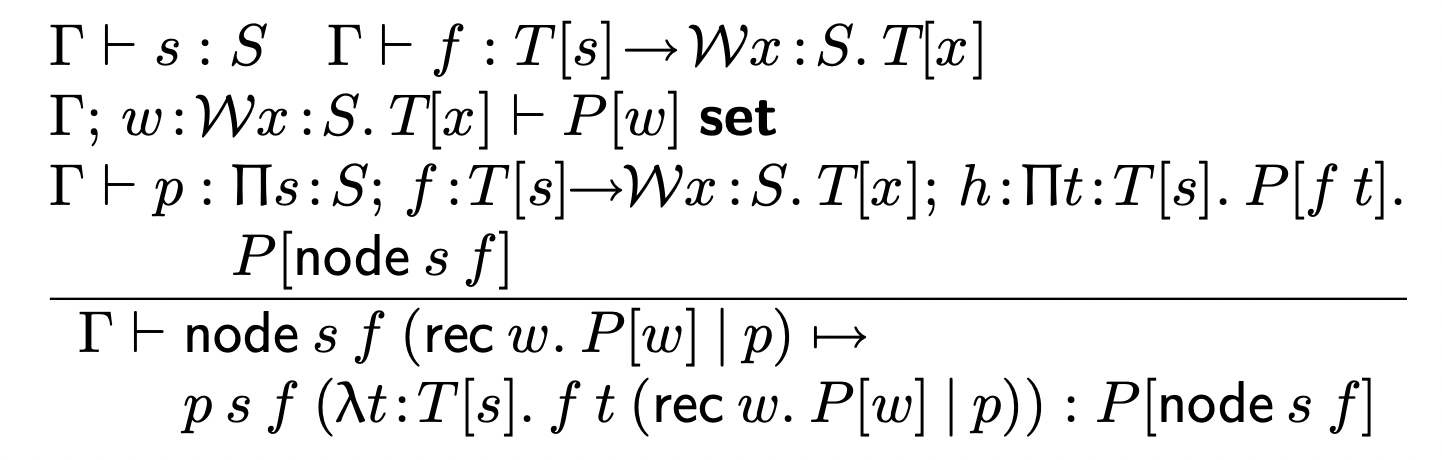
A mouthful
(sorry, didn't have time to prepare an explaination)
indNat
(n: Nat)
(P: Nat -> Type)
(base: P zero)
(inductive_hyp: (n: Nat) -> P n -> P (succ n)) : P n := {
match n with
zero => P zero
succ(m) => inductive_hyp m (indNat m P base inductive_hyp)
}
Example:
n := 3
P := n => Int
base := 1
inductive_hyp := (n, acc) => n*acc
indNat n P base inductive_hyp outputs 6
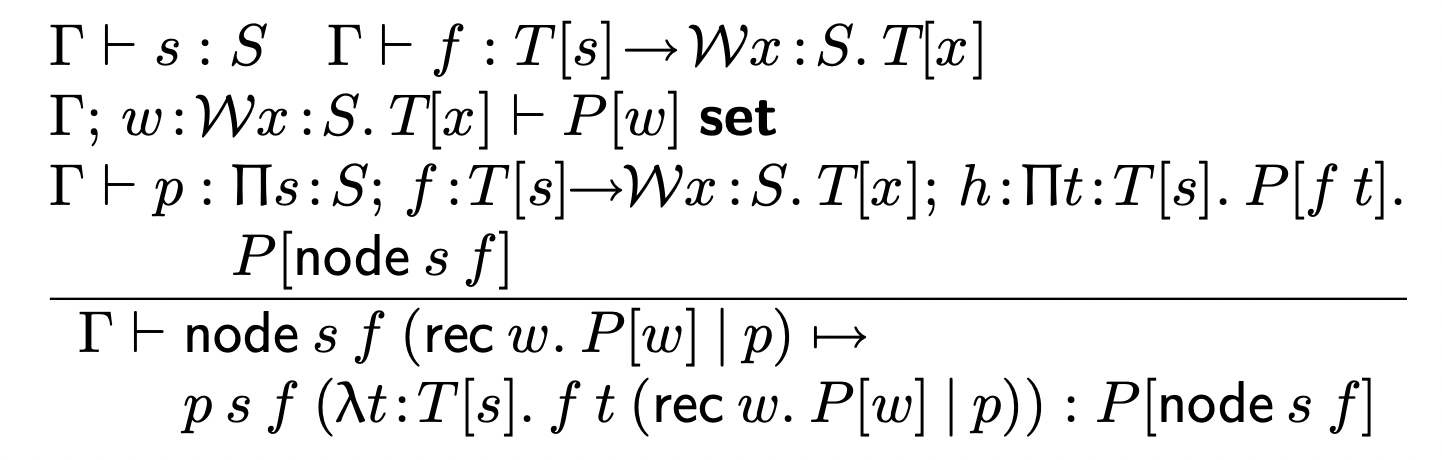
indBTree
(bt: BTree)
(P: BTree -> Type)
(leaf_p: P leaf)
(bt_node_p: (l: BTree, r: BTree) -> (P l, P r) -> P (bt_node l r)): P bt := {
match bt with
case leaf => leaf_p
case bt_node(l,r) => bt_node_p (l,r) (indBTree..., indBTree...) }
Example:
bt := BTNode(
l := BTNode(l := leaf(), r := leaf()),
r := BTNode(l := leaf(), r := leaf()))
P := n => Int,
leaf_p := 1
bt_node_p := (l,r,size_l,size_r) => size_l + size_r + 1
indBTree bt P leaf_p bt_node_p outputs 7