Linear invariants of tensors

Chris Liu

Colorado State University

July 2025

Tensors are multilinear maps

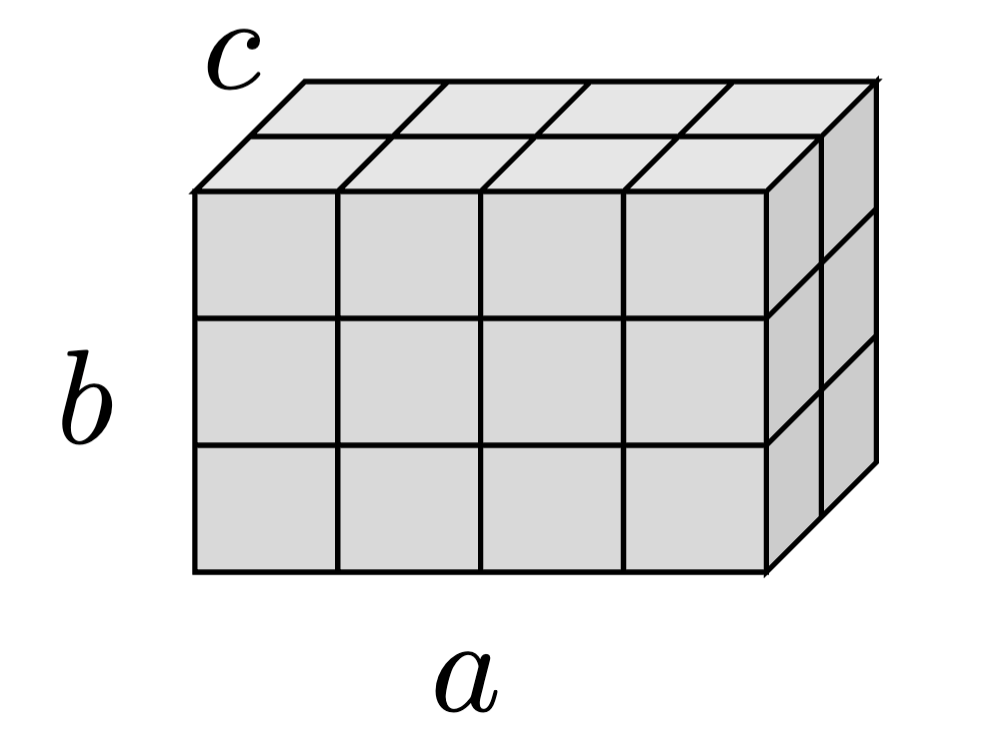
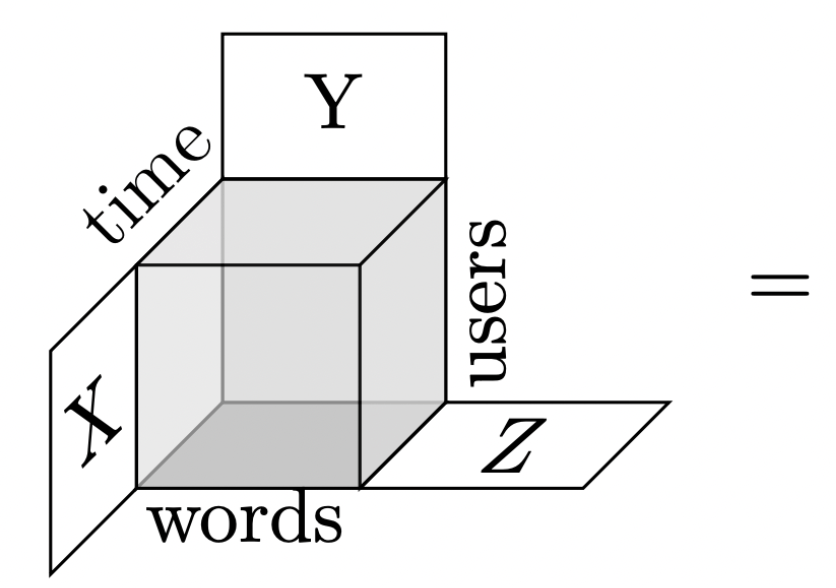
$ T $ is $ (a \times b \times c) $ grid of numbers

A multilinear interpretation: \[ \langle T \mid - \rangle: K^a \times K^b \times K^c \rightarrowtail K \] where

\[\left\langle T \; \left|\; e_i, e_j, e_k \right.\right\rangle = T_{ijk}\]

Another possible interpretation: $ [T \mid -]: K^a \times K^b \rightarrowtail K^c $, where $ [T \mid e_i,e_j] = \sum_k T_{ijk} e_k $

Example 1: Multiplication

Let $ A $ be a $K$-vector space with bilinear multiplication $ \mu: A \times A \rightarrowtail A $ (a $K$-algebra)

For ordered basis $ (e_1,\ldots, e_n )$ of $A$, coordinatize $\mu$ by a $ (n \times n \times n) $ grid of numbers $T$ satisfying $ \mu(e_i,e_j) = \sum_k T_{ijk}e_k $.

For instance, $A = K[x]/(x^2+1) $, in the basis $ \{1,x\} $

\[T_{\ast\ast 1} = \begin{bmatrix} 1 & \\ & -1\end{bmatrix}, T_{\ast\ast x} = \begin{bmatrix} & 1 \\ 1 & \end{bmatrix}\]

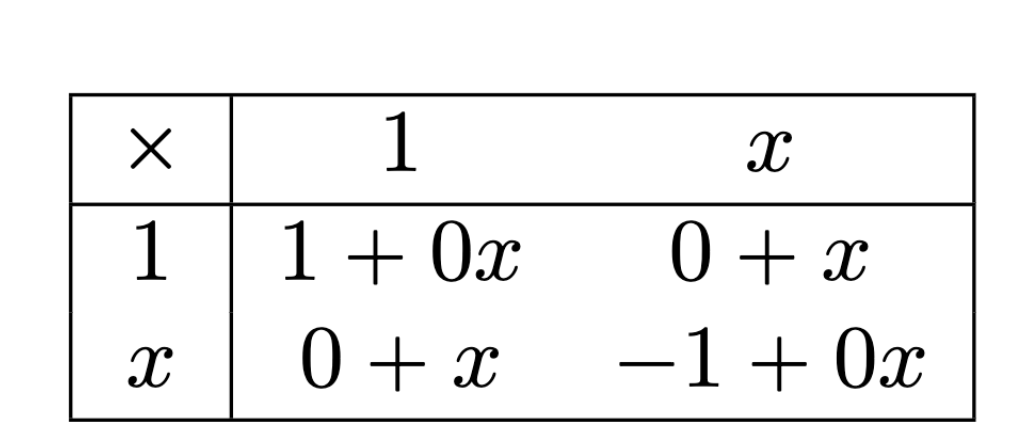
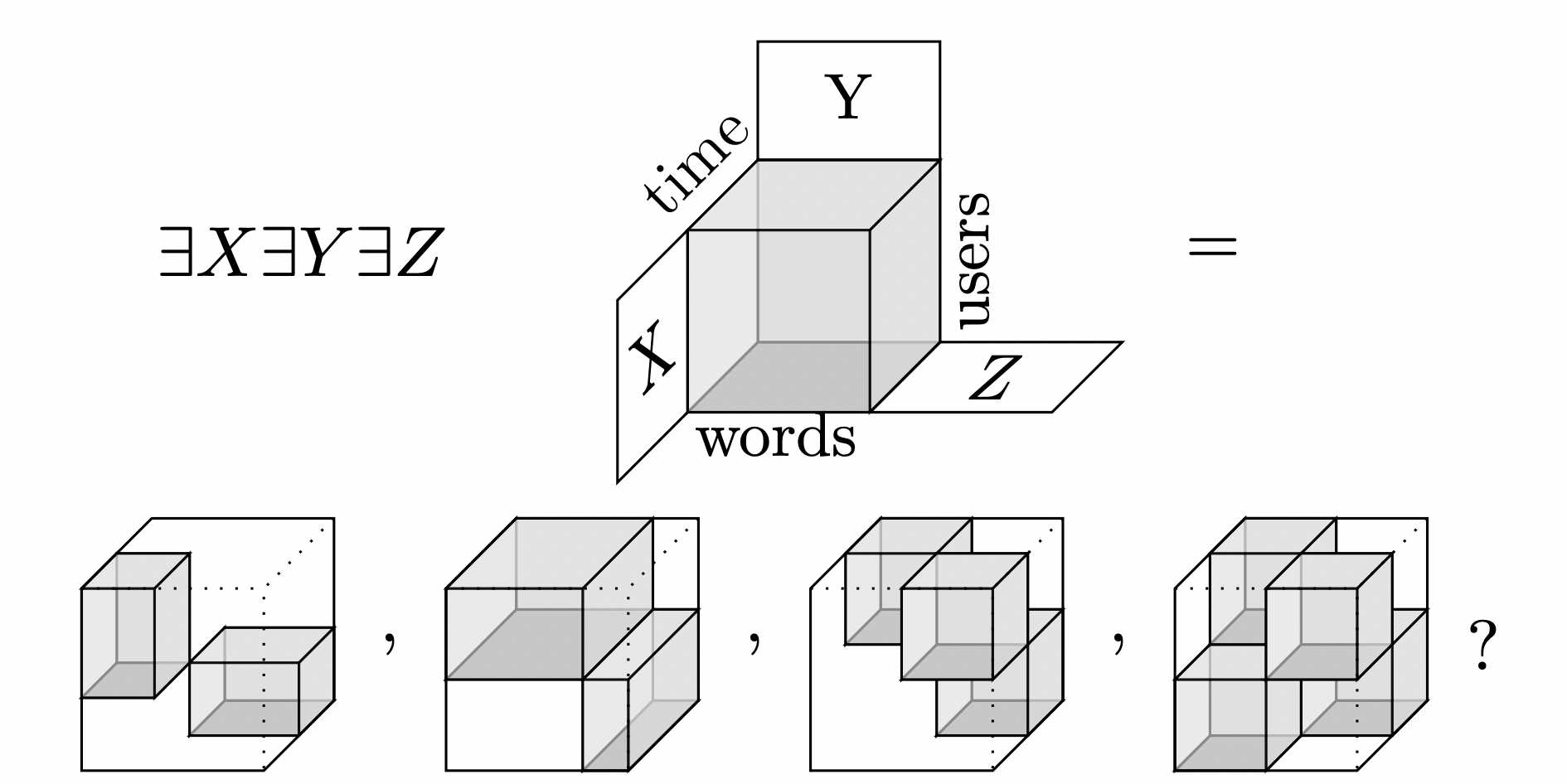
Example 2: Discord chat logs

$\text{Users}$ = $ \mathbb{R}^{\{\text{Alice}, \text{Bob}, \text{Charlie}, \ldots \}} $

$\text{Time}$ = $\mathbb{R}^{\{\text{Monday}, \text{Tuesday}, \ldots, \text{Sunday}\}} $

$\text{Words}$ = $ \mathbb{R}^{\{\text{Math}, \text{Sports}, \text{Movie}, \ldots\}} $

$ T $ is a grid storing number of occurences a user at a time used a word

$ \langle T |: \text{Users} \times \text{Time} \times \text{Words} \rightarrowtail \mathbb{R} $ can be data mined

Example: "weekend hockey group" cluster is a linear combination of Saturday, Sunday for the time axis and Chris & his hockey team in the "users" axis.

Cluster patterns of tensors from algebra

Source: Optimal Search Spaces for Tensor Problems, Figure 1.1

Myasnikov '90, Wilson '08 and others use the algebra, i.e

Adjoints detect face blocks

Theorem

Given $ *: U \times V \rightarrowtail W $

$$\operatorname{Adj}(*) = \{(X,Y) \mid (\forall u,v)Xu*v = u*Yv\}$$

Exists $\mathcal{E} = \{e_1,\ldots, e_n \} \subset \text{Adj}(*) $,

$ \sum_i e_i = 1$, and $e_ie_j = e_i $ if $ i = j $, otherwise $0$

if and only if

Exists $\perp$-decomposition, $U := \bigoplus_i U_i$ and $V := \bigoplus_i V_i $,

\[ U_i * V_j = 0, \text{ when } i \neq j \]

Has composition: $ (X,Y), (X',Y') \in \text{Adj}(*) $,

then $ (XX')u \ast v = X(X'u)*v = (X'u)*Yv = u*(Y'Y)v $

Is associative so a lot is known computationally

Example

t_1 = \begin{bmatrix} 978 & 724\\ 700 & 739 \end{bmatrix} \quad t_2 = \begin{bmatrix} 682 & 660 \\ 51 & 689 \end{bmatrix}, T = [t_1, t_2]

entries in $ \mathbb{F}_{997} $

\text{Adj}(t) = \langle (X,Y) \rangle \text{ where} \\ X = \begin{bmatrix} 0 & 1 \\ 481 & 930 \end{bmatrix} \qquad Y = \begin{bmatrix} 465 & 836\\ 648 & 465 \end{bmatrix}

M = \begin{bmatrix} 643 & 1\\ 421 & 1 \end{bmatrix} \quad N = \begin{bmatrix} 111 & 836 \\ 886 & 836 \end{bmatrix}

MXM^{-1} = \begin{bmatrix} 576 & 0 \\ 0 & 354 \end{bmatrix} \qquad NYN^{-1} = \begin{bmatrix} 576 & 0\\ 0 & 354 \end{bmatrix}

Adjoint equation of $ XT = TY $ implies $ MXM^{-1}(MTN^{-1}) = (MTN^{-1})NYN^{-1}$

"First row multipled by 576 is equal to first column multipled by 576"

implies

MTN^{-1} = \begin{bmatrix}* & 0 \\ 0 & *\end{bmatrix}

Diagonalize via

Centroids detect diagonal blocks

Given $ *: U \times V \rightarrowtail W $

$$\operatorname{Cen}(*) = \{(X,Y,Z) \mid (\forall u,v)Xu*v = u*Yv = Z(u*v) \}$$

Derivations detect surfaces

Source: Detecting cluster patterns in tensor data, Figure 3

Given $ *: U \times V \rightarrowtail W $

$$\operatorname{Der}(*) = \{(X,Y,Z) \mid (\forall u,v) \; Z(u*v) = Xu*v + u*Yv \}$$

Is commutative: $ (XX')u * v = X'u * Yv = Z(u*Yv) = Z(Xu*v) = (X'X)u*v $

Is Lie: $ XY-YX \in \text{Der}(s) $ too

Theorem (Brooksbank, Kassabov, Wilson '24)

For $ (u,v,w) $ eigenvectors of $ (X,Y,Z) $ in $ \text{Der}(*) $ with eigenvalues $ (\kappa , \lambda, \rho) $,

\[w^{\dagger}Z(u*v) = w^{\dagger}(Xu*v + u*Yv)\]

\[ \rho w^{\dagger}(u*v)-w^{\dagger}(\kappa u*v + u*\lambda v) = 0\]

By distributive property,

\[ (\rho - \kappa - \lambda) (w^{\dagger}(u *v)) = 0 \]

Conclude either $ \rho - \kappa - \lambda $ is zero or $ w^{\dagger}(u*v) $ is zero.

A tensor $ T $ with coordinates in an eigenbasis of the derivation algebra means "eigenvalues of the derivation satisfy a constraint equation at position $ (i,j,k) $" or $ T_{ijk} = 0 $

Algorithms for computation

(Joint with James B. Wilson, Joshua Maglione on "Simultaneous Sylvester System")

Coordinatized generalized adjoint problem

Such that

(\forall i) \; XA_i + B_iY = C_i

A \in K^{r \times b \times c}\\ B \in K^{a \times s \times c}\\ C \in K^{a \times b \times c}

X \in K^{a \times r}\\ Y \in K^{s \times b}

Given

Same system for module endomorphism, centralizer, and centroid problems

Find

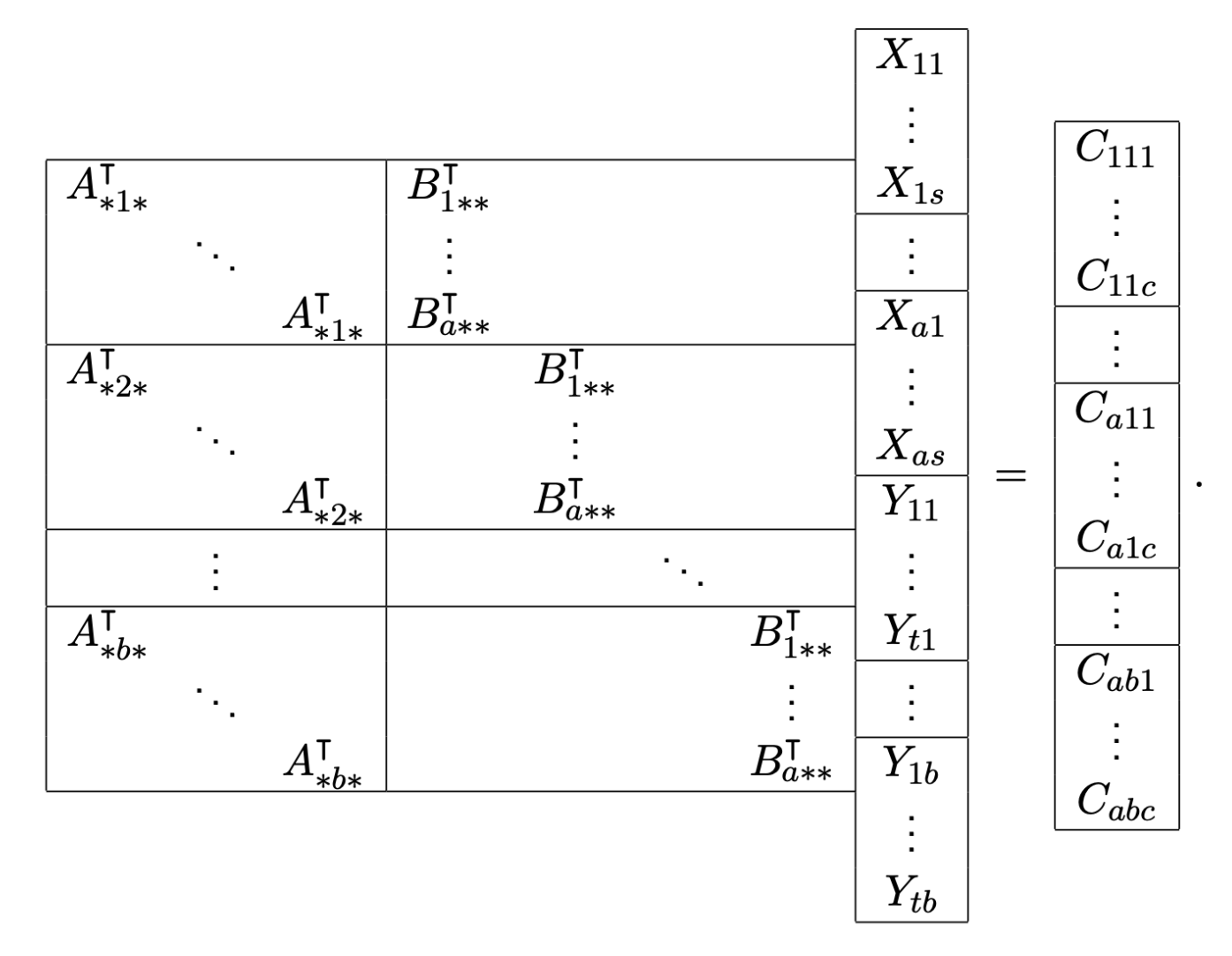
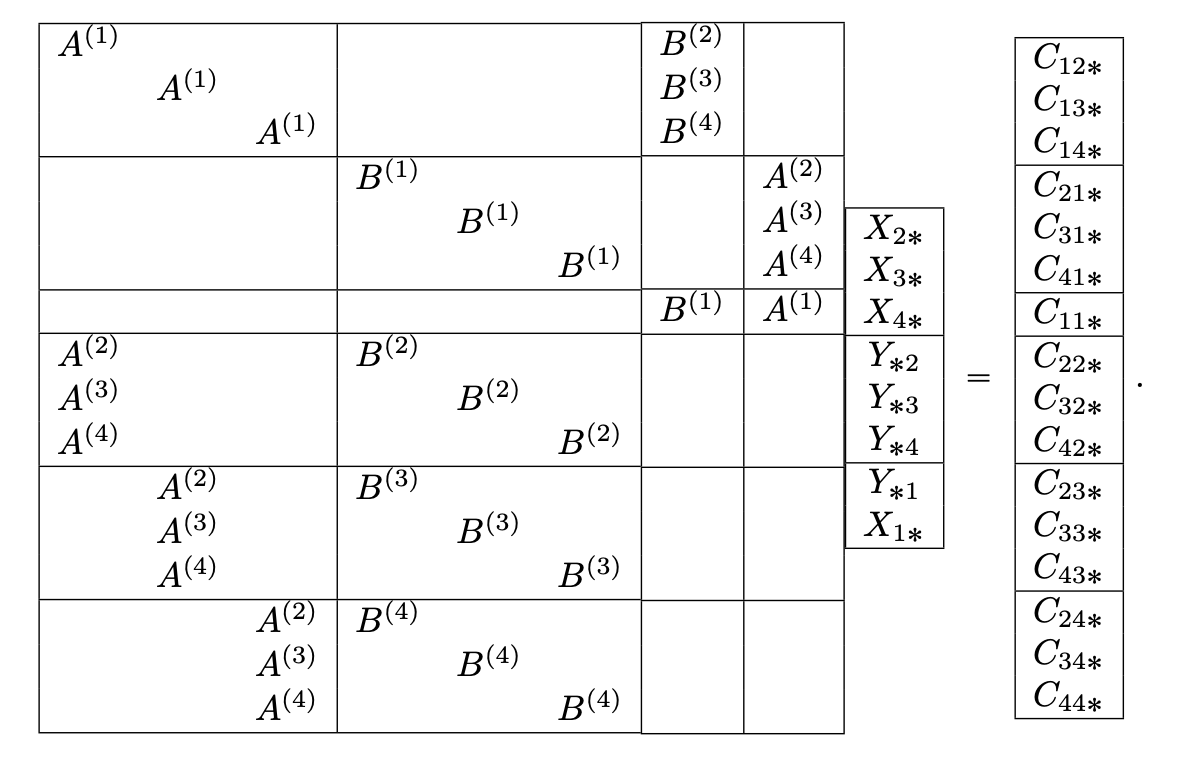
Augmented matrix of size $ (abc) \times (ar + bs) $ in standard form

> t := Random(KTensorSpace(GF(997), [20,20,20]));
> Nucleus(t,1,2);
Constructing a 800 by 8000 matrix over Finite field of size 997.
Computing the nullspace of a 800 by 8000 matrix.
Matrix Algebra of degree 40 with 1 generator over GF(997)

In Magma's multilinear algebra library

Idea: Avoid augmented matrix altogether with a solve-backsubstitute-check approach

How much to solve depends on an invertibility condition

Theorem (L.-Maglione-Wilson)

Given $ A \in K^{r \times b \times c}$, $B \in K^{a \times s \times c} $, and $C \in K^{a \times b \times c} $ an instance of SSS

If $ \text{HorizontalJoin}(A(:, 1:b', :) ) $ and $ \text{HorizontalJoin}(B(1:a', :, :) $ are full rank

Then a solution is found by solving a linear system of $a'r + b's$ variables followed by backsubstitution

For the roughly cubic ("thick") case, we expect $ a' $ and $ b' $ to be constants as function of $ n $. Reduces solving an $ O(n^2) $ variable system to an $O(n) $ variable system

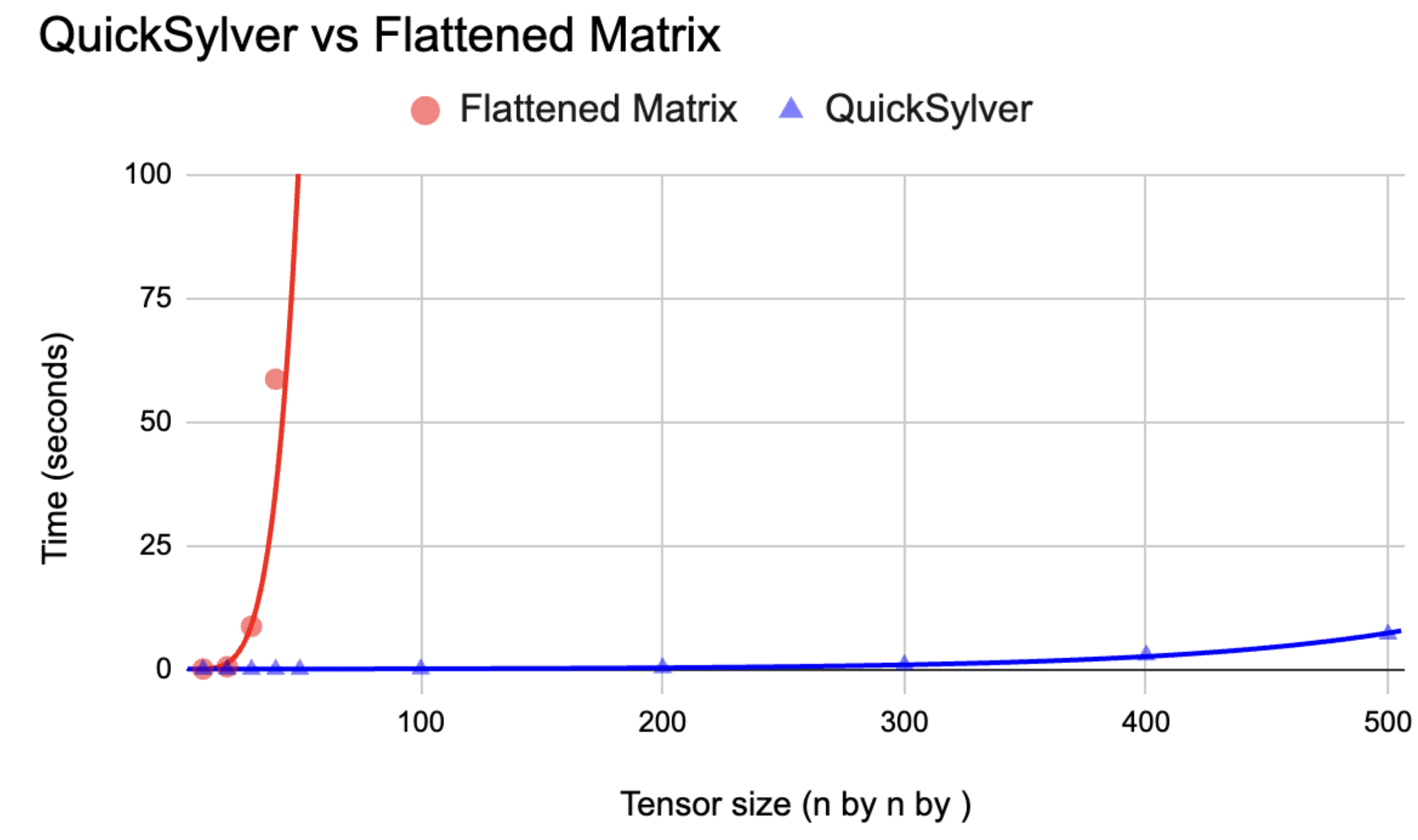
Because $ \text{Adj}(t) $ is an algebra, a few solutions suffice to generate
Code available in Magma and Julia

Distilling the idea

Let $A,B,C,R,S $ vector spaces, with fixed isomorphisms to dual.

Given
$r : \textcolor{blue}{R} \times B \times C \rightarrowtail K $,
$ s : A \times \textcolor{green}{S} \times C \rightarrowtail K $,
$ t : A \times B \times C \rightarrowtail K $

Find
$ x : A \rightarrow \textcolor{blue}{R}, y : B \rightarrow \textcolor{green}{S} $ such that,

\[ r(x(a),b,c) + s(a,y(b),c) = t(a,b,c)\]

for all $ (a,b,c) $ in $ A \times B \times C $

View $ r: R \rightarrow B \otimes C, s: S \rightarrow A \otimes C $ through isomorphisms to dual

Compute simultaneous sylvester equation restricted to $A'$ and $ B' $

Solve dense system

Backsubstitute for rest of solutions

Use left inverses to isolate unknown

Find subspaces $ A' \leq A, B' \leq B $ of small dimension so $ \tilde{r} : R \hookrightarrow B' \otimes C$ and $\tilde{s} : S \hookrightarrow A' \otimes C $ are injective (left invertible)

r(x'(a'),b'c) + s(a',y'(b'),c) = t(a',b',c)

\text{Find } x': A' \rightarrow R \text{ and }y': B' \rightarrow S \text{ such that } \\

\tilde{r}^{\#} \circ (\tilde{r} \circ x'' + s \circ y') = \tilde{r}^{\#}\circ \tilde{t}\\ \text{hence } x'' = \tilde{r}^{\#} \circ (\tilde{t} - s \circ y')

\text{Given x$'$, y$'$, find } x'': U \rightarrow R \text{ by solving} \\

Derivations are similar!

A \in K^{r \times b \times c}\\ B \in K^{a \times s \times c}\\ C \in K^{a \times b \times t}

X \in K^{a \times r}\\ Y \in K^{s \times b}\\ Z \in K^{t \times c}

Given

Find

Such that

(\forall i) \; XA_i + B_iY = \sum_j C_jZ_{ji}

There are strong theoretical reasons that solving this derivation equation captures all information an algebra can see about the tensor. See Theorem A

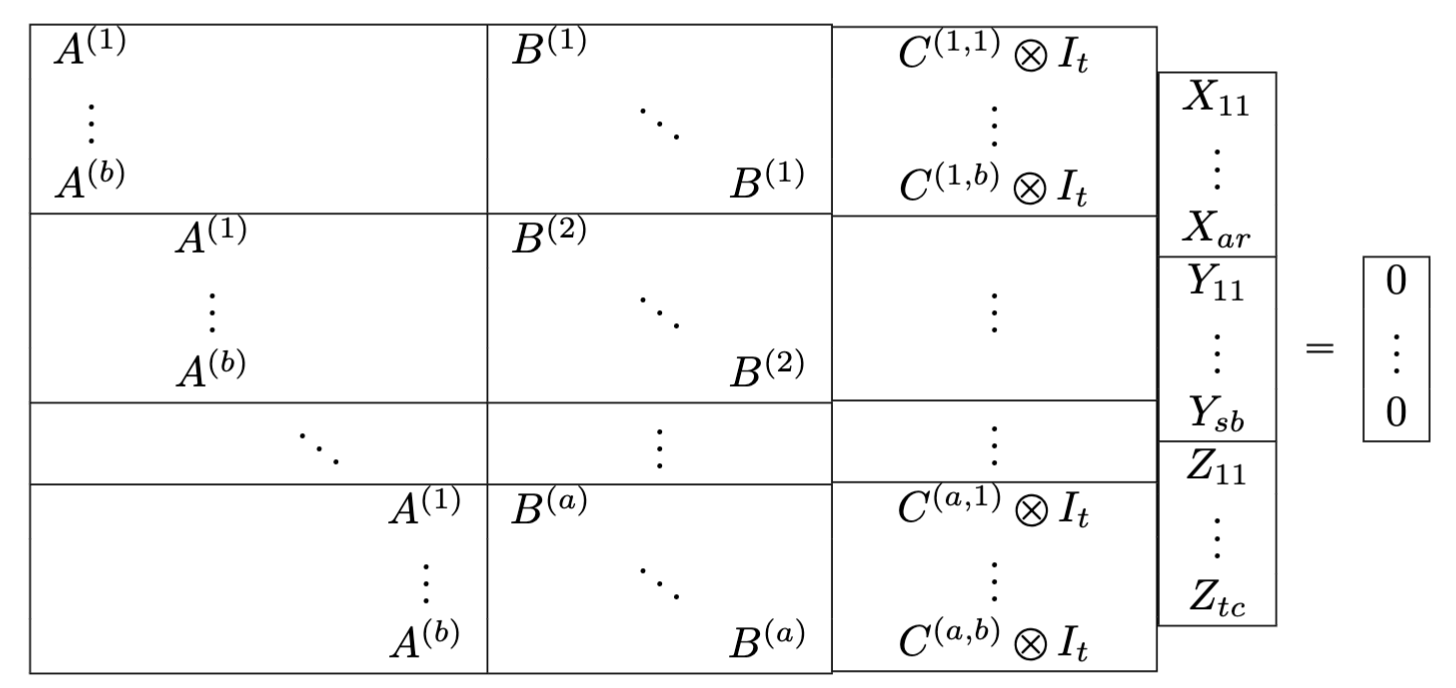
Augmented matrix of size $ (abc) \times (ar + bs + ct) $

Use idea from adjoint case

Let $A,B,C,R,S, T $ vector spaces, with fixed isomorphisms to dual.

Given
$r : \textcolor{blue}{R} \times B \times C \rightarrowtail K $,
$ s : A \times \textcolor{green}{S} \times C \rightarrowtail K $,
$ t : A \times B \times \textcolor{orange}{T} \rightarrowtail K $

Find
$ x : A \rightarrow \textcolor{blue}{R}, y : B \rightarrow \textcolor{green}{S}, z : C \rightarrow \textcolor{orange}{T} $ such that

\[ r(x(a),b,c) + s(a,y(b),c) = t(a,b,z(c)) \]

for all $ (a,b,c) $ in $ A \times B \times C $

View $ r: R \rightarrow B \otimes C, s: S \rightarrow A \otimes C, t: T \rightarrow A \otimes B $ through isomorphisms to dual

Compute derivation restricted to $A'$, $ B' $, and $ C' $

Solve dense system

Backsubstitute for rest of solutions

Use left inverses to isolate unknown

Find subspaces $ A' \leq A, B' \leq B, C' \leq C $ of small dimension so $ \tilde{r} : R \hookrightarrow B' \otimes C'$, $\tilde{s} : S \hookrightarrow A' \otimes C' $, and $\tilde{t} : T \hookrightarrow A' \otimes B' $ are injective (left invertible)

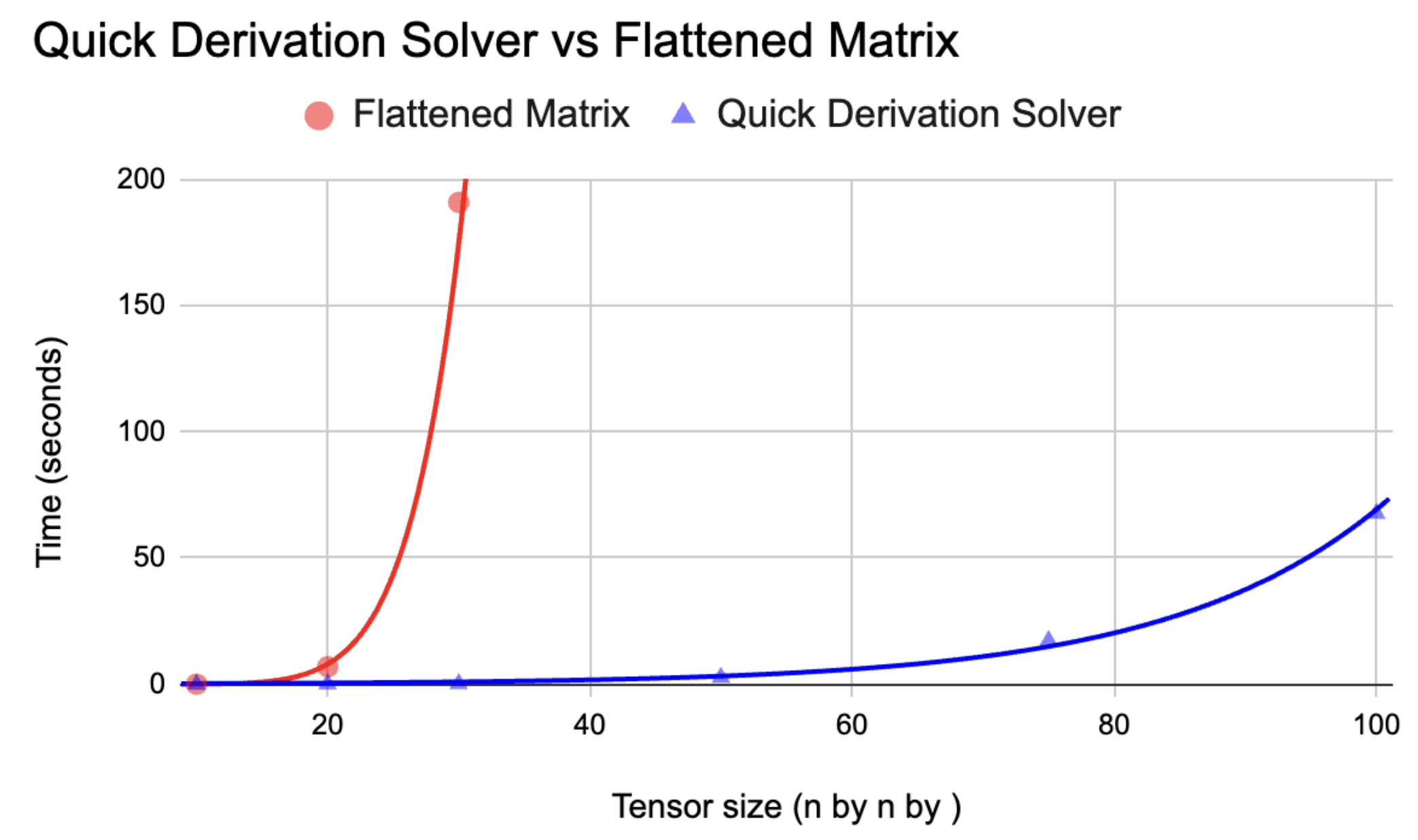
Code available in Julia and Magma (soon)

Linear invariants of tensor products

Let $ A, B $ be unital associative $ K $-algebras

Observation: $ A \otimes B $ is a K-algebra, with multiplication
\[ (a \otimes b)(c \otimes d) = ac \otimes bd \]

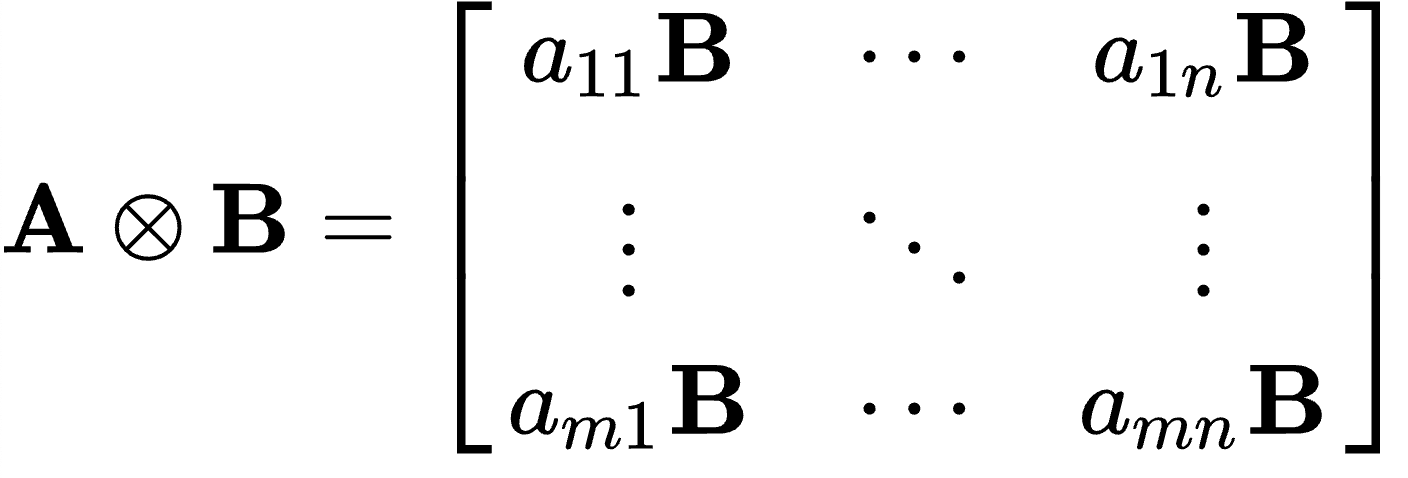
Example: Kronecker product of matricies

Extend to their multiplication tensors

For $ s: A \times A \rightarrowtail A$ and $t: B \times B \rightarrowtail B $, define $ s \otimes t: (A \otimes B) \times (A \otimes B) \rightarrowtail (A \otimes B) $ as

\[ \langle s \otimes t \mid a \otimes b, c \otimes d \rangle = \langle s|a,c\rangle \otimes \langle t|b,d \rangle \]

\begin{array}{|c|cc|} \hline & 1 & x \\ \hline 1 & 1 & x \\ x & x & -1 \\ \hline \end{array} \otimes \begin{array}{|c|cc|} \hline & 1 & y \\ \hline 1 & 1 & y \\ y & y & -5y-10 \\ \hline \end{array} = \begin{array}{|c|cccc|} \hline & 1 & x & y & xy \\ \hline 1 & 1 & x & y & xy \\ x & x & -1 & xy & -y \\ y & y & xy & -5y-10 & -5xy-10x \\ xy & xy & -y & -5xy-10x & 5y+10 \\ \hline \end{array}

Example: Bilinear over a bigger field

r_1 = \begin{bmatrix} 7 & 10 & 4 & 2\\ 10 & 12 & 2 & 5\\ 1 & 7 & 11 & 12\\ 7 & 11 & 12 & 4 \end{bmatrix} \quad r_2 = \begin{bmatrix} 5 & 6 & 1 & 9 \\ 6 & 1 & 9 & 8 \\ 10 & 12 & 6 & 2\\ 12 & 2 & 2 & 9 \end{bmatrix}

Over $K = \mathbb{F}_{13}$, let $r: K^4 \times K^4 \rightarrowtail K^2 $ given by

t_1 = \begin{bmatrix} 10 & 5\\ 5 & 6 \end{bmatrix} \quad t_2 = \begin{bmatrix} 9 & 3\\ 3 & 7 \end{bmatrix}

T gives coordinates of $ K[x]/(x^2+8x+11) \cong \mathbb{F}_{13^2} $ multiplication

in $ \{ 3+4x, 7+10x \} $ basis

Centroid algebra detects $ r $ is $ \mathbb{F}_{13^2} $ bilinear

Hence $r $ is equal to $ s \otimes t $ for $s : K^2 \times K^2 \rightarrowtail K $ and t multiplication in $ \mathbb{F}_{13^2} $. Indeed,

s = \begin{bmatrix} 2 & 3 \\ 4 & 5 \end{bmatrix}

$ \text{Adj}(s \otimes t) = \text{Adj}(s) \otimes \text{Adj}(t) $

$ \text{Der}(s \otimes t) $ = $ \text{Der}(s) \otimes \text{Cen}(t) + \text{Cen}(t) \otimes \text{Der}(s) + \text{Nuc}_{ij}(s \otimes t) $

Linear invariants under tensor products

Theorem (L.)

(Results generalize known results in non-associative algebra, i.e Brešar)

Main ideas

$ \mu \in \text{Adj}(s \otimes t)$ implies $ \mu = \left(\sum_i \sigma^{(2)}_i \otimes \tau^{(2)}_i, \sum_j \sigma^{(1)}_j \otimes \tau^{(1)}_j \right) \in \text{End}(U \otimes X) \times \text{End}(V \otimes Y) $
In Adj means $\langle s \otimes t|\mu = 0$, expand as $\sum_i a_i \otimes b_i = \sum_j c_j \otimes d_j $, where $a_i = \langle s|\sigma^{(2)}_i $ and so forth
Since $ a_i \in \text{span}\{c_j\}$ and $b_i \in \text{span}\{d_j\} $, conclude $ (a_1 \otimes b_1) = (\sum_j \lambda_j c_j) \otimes (\sum_k \rho_k d_k) $
Writes $\mu$ as sum of terms in $ \text{Adj}(s) \otimes \text{Adj}(t)$
For Der, more cases since equation is $ \sum_i a_i \otimes b_i = \sum_j c_j \otimes d_j + \sum_k e_k \otimes f_k $.

Given $ s: U \times V \rightarrowtail W, t: X \times Y \rightarrowtail Z $

$ s \otimes t : (U \otimes X) \times (V \otimes Y) \rightarrowtail (W \otimes Z) $

Definition [Derivation Closure] (First, Maglione, Wilson '20)

$ (| t |) = \{ s: U \times V \rightarrowtail W \mid \operatorname{Der}(t) \subseteq \operatorname{Der}(s) \} $

Theorem (FMW)

Central simple algebras have one dimensional derivation closures

Observation

$ \text{Der}(t) \subset \text{Der}(s)$ implies $ (|s|) \subset (|t|) $

What tensors satisfy some given linear invariant?

Theorem (L.)
$ (| s \otimes t |) = (| s |) \otimes (| t |) $

For $ s: U \times V \rightarrowtail W $ and $t: X \times Y \rightarrowtail Z $

Define $ s \otimes t: (U \otimes X) \times (V \otimes Y) \rightarrowtail (W \otimes Z) $ as
\[ \langle s \otimes t | u\otimes x, v \otimes y \rangle = \langle s | u,v \rangle \otimes \langle t | x,y \rangle \]

Tensor product of bilinear maps

Extend to bilinear maps

Linear invariants of tensors

Tensors are multilinear maps

Example 1: Multiplication

Example 2: Discord chat logs

Cluster patterns of tensors from algebra

Adjoints detect face blocks

Example

Centroids detect diagonal blocks

Derivations detect surfaces

Algorithms for computation

Coordinatized generalized adjoint problem

Distilling the idea

Derivations are similar!

Augmented matrix of size \( (abc) \times (ar + bs + ct) \)

Use idea from adjoint case

Linear invariants of tensor products

Linear invariants under tensor products

Theorem (L.)

What tensors satisfy some given linear invariant?

Tensor product of bilinear maps

End