Simultaneous Sylvester Systems (SSS) and some applications
Chris Liu (chris.liu@colostate.edu)
Colorado State University
June 2025
Joint with James B. Wilson and Joshua Maglione


I bring this waterbottle with me everywhere and will probably lose it once this week!
Center
\( \{ X \in A \;|\; (\forall i) \;XA_i = A_i X \} \)
Centralizer & Module End
\( \{ X \in \mathbb{M}_n(K) \;|\; (\forall i) \; XA_i = A_i X \} \)
Centroid algebra
\( \left\{ (X,Y,Z) \in \mathbb{M}_n(K) \times \mathbb{M}_m(K) \times \mathbb{M}_c(K) \;|\; (\forall i) \; XT_{i} = T_{i}Y = \left(\sum_j Z_{ij}T_j \right)_i \right\} \)
Module hom
\( \{ X \in \mathbb{M}_{n\times m}(K) \;|\; (\forall i) \;XA_i = B_i X \} \)
Adjoint algebra
\( \{ (X,Y) \in \mathbb{M}_n(K) \times \mathbb{M}_m(K) \;|\; (\forall i) \; XT_{i} = T_{i} Y \} \)
Given \(A = \langle A_1,\ldots, A_c \rangle \) a matrix algebra
Given \( T = [T_{1}, \ldots, T_{c}] \) with \(T_{i} \in \mathbb{M}_{n \times m}(K) \) - a tensor
For lists of \(n \times n\) matricies, decades of rich theory to avoid solving linear system of \( n^2 \) variables
Center
Using randomization - Friedl-Ronyai '85, Ivanyos–Rónyai '94, Eberly-Giesbrecht '96,...
Centralizer & Module End
Case of module hom
Module hom
Meataxe - Horton-Parker '84 Holt-Rees '94, Ivanyos-Lux '00, ...
Condensation - Thackray '81, Ryba '90, Lux-Wiegelmann '95, Lübeck-Neunhöffer '01, ...
Peakwords - Lux-Szöke '03
Adjoint algebra
Kronecker modules for \( c = 2 \) - Brooksbank-Maglione-Wilson '17
Centroid algebra
Optimizations for c = 2 case in Magma
A bottleneck example
Question: Does there exist an element in \( \operatorname{End}_A(M) \) of the form
\( \begin{bmatrix} I_n & \ast & 0 \\ 0 & I_n & \ast \\ 0 & 0 & I_n \end{bmatrix} \)
- Local algebra, no idempotents to split
- Many non-redundant generators as \(A_iA_j\) only adds on the (1,2) and (2,3) blocks.
\( \begin{bmatrix} X & U & W \\ 0 & Y & V \\ 0 & 0 & Z \end{bmatrix} \in \operatorname{End}_A(M)\) satisfies
Centralizer-like relations need to be satisfied for all \(i \)
Currently, no better ideas than solving \(2n^2\) variable linear systems in \(n^3\) equations
- Not a center, centralizer, or module endomorphism question
- End of the line for algebra splitting and radical layers splitting of original algebra
Our case: \( X = Y = Z = I_n \) and we just need \( U B_i = A_i V\)
Magma example code here showcase slow
Mention difference compared to unitraingular (non-blocked) case or other theory cases where work bottoms out to tiny systems

Create \( B_i \) from \(A_i \)
Create \(B_i\) randomly

(SSS) Simultaneous Sylvester Systems
Given
Find
Such that
\( i \in \{1,\ldots, c\} \)
Center, module end/hom, adjoint, centroid all instances
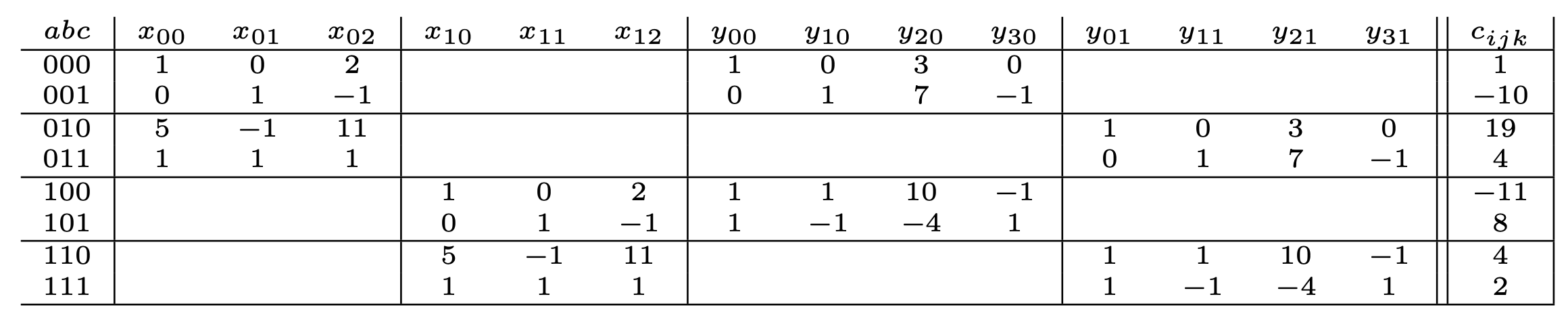
Without assuming other structure, there is interwoven striding in augmented matrix of flattened linear system
The fine print
\( K = \text{GF}(5)\) here and throughout
Bottleneck module end problem is for the below module in Magma
Yet this system scales like solving system of \(n^2\) variables
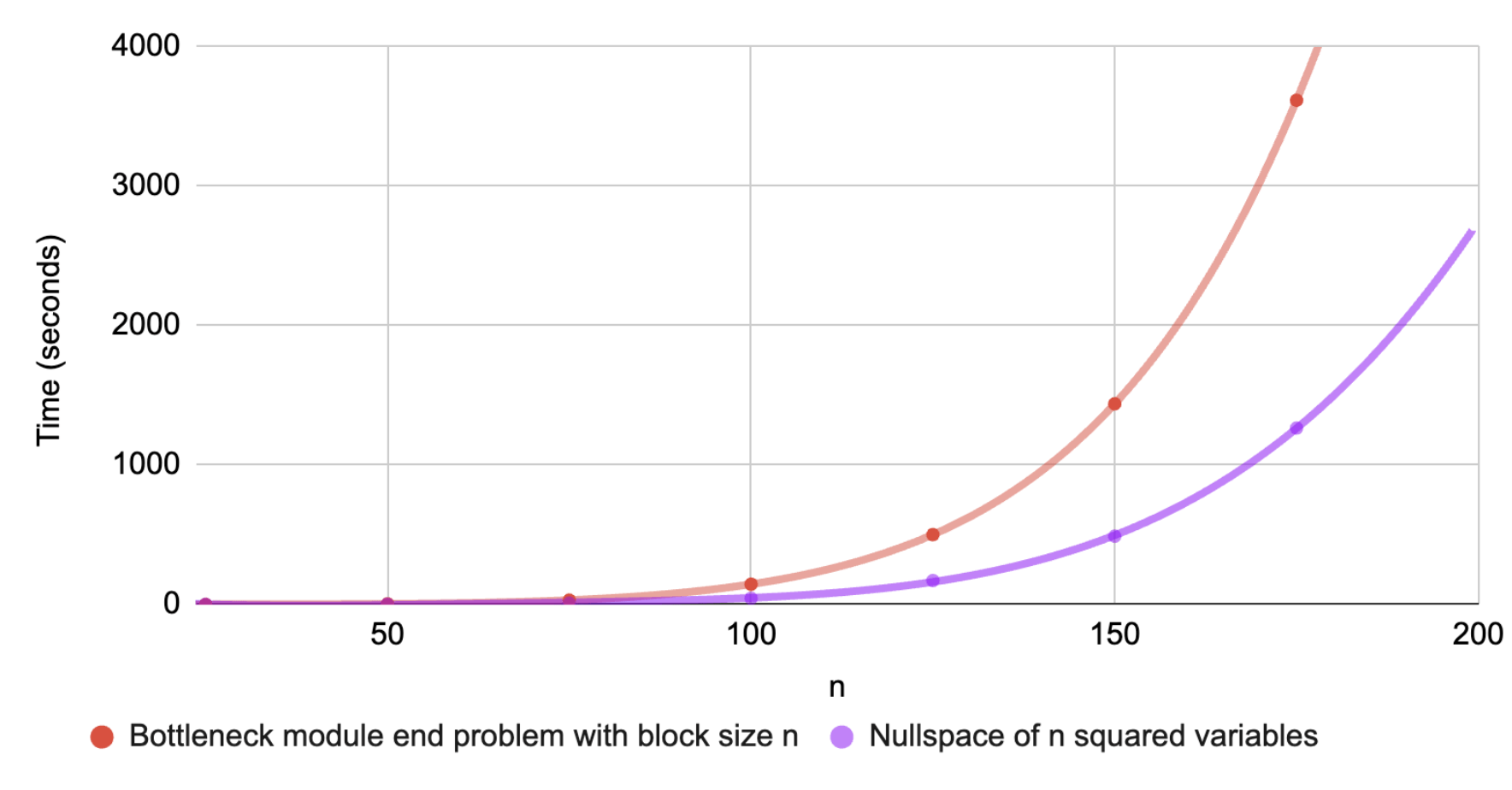
How much to solve depends on an invertibility condition
Theorem (L.-Maglione-Wilson)
Given \( A \in K^{r \times b \times c}\), \(B \in K^{a \times s \times c} \), and \(C \in K^{a \times b \times c} \) an instance of SSS
If \( \text{HorizontalJoin}(A(:, 1:b', :) ) \) and \( \text{HorizontalJoin}(B(1:a', :, :) \) are full rank
Then a solution to SSS is found by solving a linear system of \(a'r + b's\) variables followed by backsubstitution
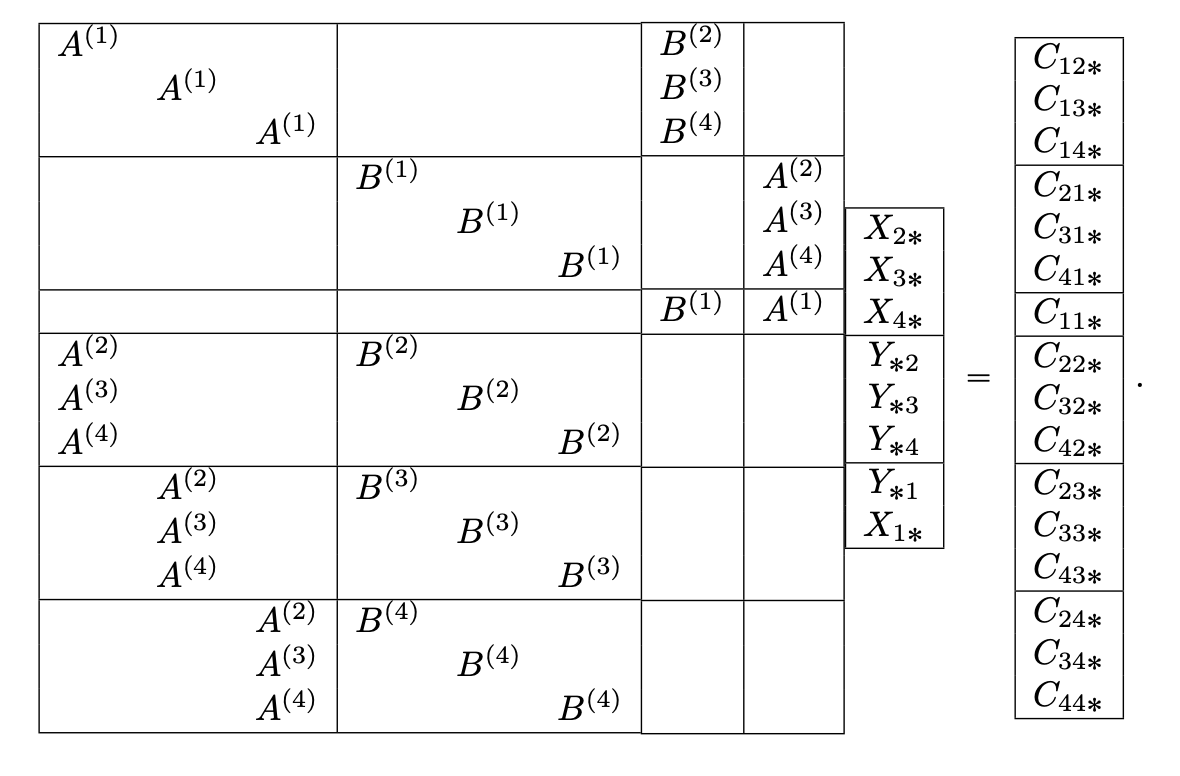
Idea: Avoid augmented matrix altogether with a solve-backsubstitute-check approach
For the roughly cubic ("thick") case, we expect \( a' \) and \( b' \) to be constants as function of \( n \). Reduces solving an \( O(n^2) \) variable system to an \(O(n) \) variable system
Being able to bound \( n' \) to be much smaller than \( n\) is a complexity win
(More precisely)
Solving a linear system of \( 2nn'\) variables
Two one-sided inverses of \(n \times nn'\) matricies
Two products of \( n^2 \times n \) matrix with \( n \times n' \) matrix
Two products of \( n \times nn' \) matrix with \( nn' \times n \) matrix
Instead of solving a system of \(ar + bs \) variables in \(abc \) equations, below are precisely the computations necessary in QuickSylver (bullet point are the variables in code)
- Solving a linear system of \( a'r + b's \) variables
- Optimization: don't take all constraints, check correctness at the end
- One-sided inverses of \( r \times b'c \) and \( s \times a'c \) matrices
- `r_B_prime` and `s_A_prime`
- The product of a \( c(a-a') \times s \) matrix with a \( s \times b' \) matrix
- `sy_U_B_prime_stacked`
- The product of a \( a' \times r \) matrix with a \( r \times c(b-b') \) matrix
- `rx_A_prime_V_stacked`
- The subtraction of two \( (a-a') \times b'c \) matricies
- (I) t_U_B_prime_stacked - sy_U_B_prime_stacked
- The subtraction of two \( (b-b') \times a'c \) matricies
- (II) t_A_prime_V_stacked - rx_A_prime_V_stacked
- The product of a \( (a-a') \times b'c\) matrix with a \( b'c \times r\) matrix
- Multiplying (I) with `r_B_prime_inv`
- The product of a \( (b-b') \times a'c \) matrix with a \( a'c \times s \) matrix
- Multiplying (II) with `s_A_prime_inv`
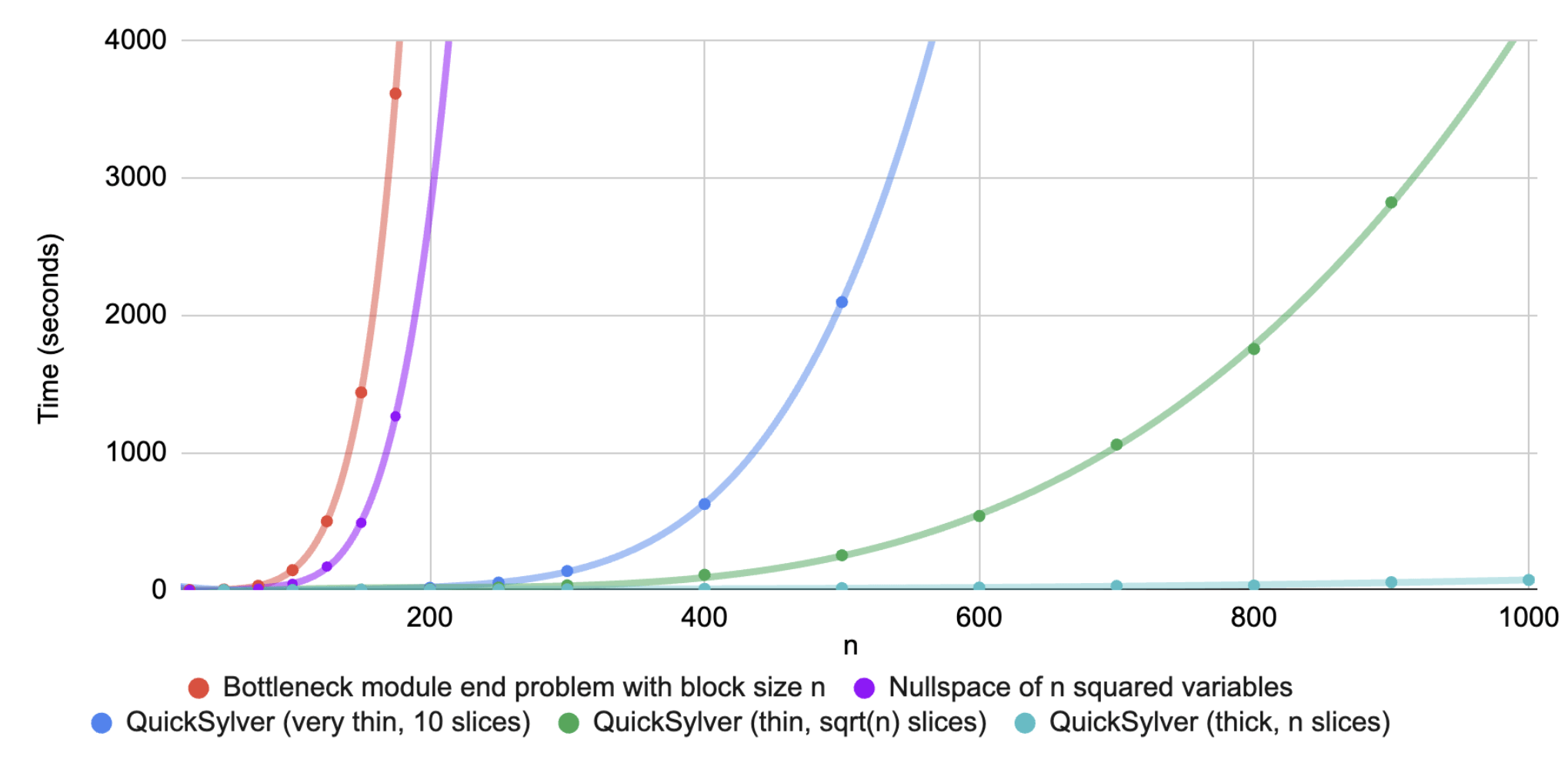
Magma implementation results
The fine print
- Only provides a specific solution, not full basis of nullspace (tunable!)
- Randomized check of solution correctness (tunable!)
- Bottleneck module end problem is for the below module in Magma
Clustering and data science application
\( T = [T_1, \ldots, T_c] \) with \(T_i \in \mathbb{M}_{n \times m}(K) \) given linear data from an external source
Solving for the adjoint algebra by a Simultaneous Sylvester Equation and decomposing it clusters original data
Example: The \( (j,k) \) entry of \( T_i \) stores number of occurences user \(i\) at time \(j\) chatted word \(k\) - called the "chatroom tensor" in the literature
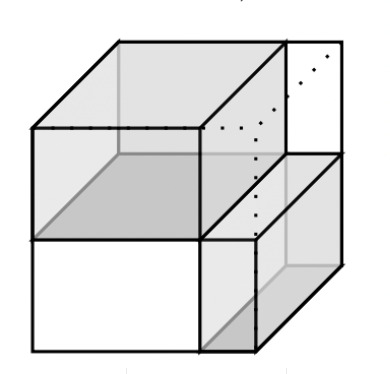
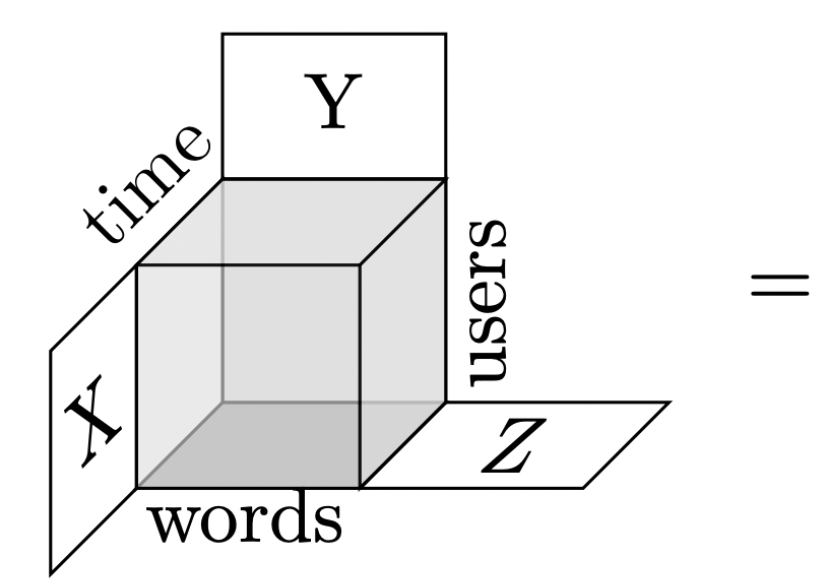
- Can hybrid approaches win even more?
- Are there bottleneck cases to try in your problems?
- Solving generalizations of SSS?
Questions?
Find us (Chris Liu, James B. Wilson, and Josh Maglione) at software demo session if interested!