pollev.com/chrismakler

Preferences and Utility

Christopher Makler

Stanford University Department of Economics

Econ 50: Lecture 5

🐟

🥥

Production Possibilities Fronier

Feasible

Lecture 4: The PPF

Lecture 2: Production Functions

Labor

Fish

🐟

Capital

Coconuts

🥥

[GOODS]

⏳

⛏

[RESOURCES]

🐟

🥥

🙂

😀

😁

😢

🙁

Today: Preferences

How does Chuck rank

all possible combinations

of fish and coconuts?

Goal: find the best combination within his production possibilities set.

Feasible

Today's Agenda

Today: Modeling Preferences with Utility Functions

Wednesday: Some "canonical" utility functions

Preferences: Definition and Axioms

Indifference curves

The Marginal Rate of Substitution

Utility Functions

Perfect Substitutes

Perfect Complements

Cobb-Douglas

Quasilinear

 

Preferences

Preferences: Ordinal Ranking of Options

Given a choice between option A and option B, an agent might have different preferences:

A \succ B
A \succeq B
A \sim B
A \preceq B
A \prec B

The agent strictly prefers A to B.

The agent strictly disprefers  A to B.

The agent weakly prefers  A to B.

The agent weakly disprefers  A to B.

The agent is indifferent between A and B.

Sidebar: “Strictly" vs. “Weakly"

A \succ B
A \succeq B

The agent strictly prefers A to B.

The agent weakly prefers  A to B.

2
3
4
5
6
x \ge 3
x \gt 3

Preference Axioms

Complete

Transitive

Any two options can be compared.

If \(A\) is preferred to \(B\), and \(B\) is preferred to \(C\),
then \(A\) is preferred to \(C\).

\text{For any options }A\text{ and }B\text{, either }A \succeq B \text{ or } B \succeq A
\text{If }A \succeq B \text{ and } B \succeq C\text{, then } A \succeq C

Together, these assumptions mean that we can rank
all possible choices in a coherent way.

Special case: choosing between bundles
containing different quantities of goods.

Preferences over Quantities

A=(4,3,6)

Example: “good 1” is apples, “good 2” is bananas, and “good 3” is cantaloupes:

🍏🍏🍏🍏

🍌🍌🍌

🍈🍈🍈🍈🍈🍈

B=(3,8,2)

🍏🍏🍏

🍌🍌🍌🍌🍌🍌🍌🍌

🍈🍈

General framework: choosing between anything

Special Case: Two Goods

Good 1 \((x_1)\)

Good 2 \((x_2)\)

Completeness axiom:
any two bundles can be compared.

Implication: given any bundle \(A\),
the choice space may be divided
into three regions:

preferred to A

dispreferred to A 

indifferent to A 

Indifference curves cannot cross!

Marginal Rate of Substitution

X = (10,24)

🍏🍏

🍏🍏

🍏🍏

🍏🍏

🍏🍏

🍌🍌🍌🍌

🍌🍌🍌🍌

🍌🍌🍌🍌

🍌🍌🍌🍌

🍌🍌🍌🍌

🍌🍌🍌🍌

Y=(12,20)

🍏🍏

🍏🍏

🍏🍏

🍏🍏

🍏🍏

🍏🍏

🍌🍌🍌🍌

🍌🍌🍌🍌

🍌🍌🍌🍌

🍌🍌🍌🍌

🍌🍌🍌🍌

Suppose you were indifferent between the following two bundles:

Starting at bundle X,
you would be willing
to give up 4 bananas
to get 2 apples

Let apples be good 1, and bananas be good 2.

Starting at bundle Y,
you would be willing
to give up 2 apples
to get 4 bananas

MRS = {4 \text{ bananas} \over 2 \text{ apples}}
= 2\ {\text{bananas} \over \text{apple}}

Visually: the MRS is the magnitude of the slope
of an indifference curve

Utility Functions

How do we model preferences mathematically?

Approach: assume consuming goods "produces" utility

Production Functions

Labor

Fish

🐟

Capital

⏳

⛏

[RESOURCES]

Utility Functions

Utility

😀

[GOODS]

Fish

🐟

Coconuts

🥥

Representing Preferences with a Utility Function

u(a_1,a_2) > u(b_1,b_2)
u(a_1,a_2) \ge u(b_1,b_2)
u(a_1,a_2) = u(b_1,b_2)
u(a_1,a_2) \le u(b_1,b_2)
u(a_1,a_2) < u(b_1,b_2)
u(x_1,x_2)

"A is strictly preferred to B"

Words

Preferences

Utility

A \succ B
A \succeq B
A \sim B
A \preceq B
A \prec B

"A is weakly preferred to B"

"A is indifferent to B"

"A is weakly dispreferred to B"

"A is strictly dispreferred to B"

Suppose the "utility function"

assigns a real number (in "utils")
to every possible consumption bundle

We get completeness because any two numbers can be compared,
and we get transitivity because that's a property of the operator ">" 

Marginal Utility

MU_1(x_1,x_2) = {\partial u(x_1,x_2) \over \partial x_1}
MU_2(x_1,x_2) = {\partial u(x_1,x_2) \over \partial x_2}

Given a utility function \(u(x_1,x_2)\),
we can interpret the partial derivatives 
as the "marginal utility" from
another unit of either good:

Indifference Curves and the MRS

Along an indifference curve, all bundles will produce the same amount of utility

In other words, each indifference curve
is a level set of the utility function.

The slope of an indifference curve is the MRS. By the implicit function theorem,

MRS(x_1,x_2) = \frac{\partial u(x_1,x_2) \over \partial x_1}{\partial u(x_1,x_2) \over \partial x_2} = {MU_1 \over MU_2}

(Note: we'll treat this as a positive number, just like the MRTS and the MRT)

If you give up \(\Delta x_2\) units of good 2, how much utility do you lose?

If you get \(\Delta x_1\) units of good 1, how much utility do you gain?

\Delta u \approx \Delta x_2 \times MU_2
\Delta u \approx \Delta x_1 \times MU_1

If you end up with the same utility as you begin with:

\Delta x_2 \times MU_2 \approx \Delta x_1 \times MU_1
{\Delta x_2 \over \Delta x_1} \approx {MU_1 \over MU_2}

pollev.com/chrismakler

What is the MRS of the utility function \(u(x_1,x_2) = x_1x_2\)?

MRS = {MU_1 \over MU_2} =
u(x_1,x_2) = x_1x_2
MU_1 = {\partial u(x_1,x_2) \over \partial x_1} =
MU_2 = {\partial u(x_1,x_2) \over \partial x_1} =

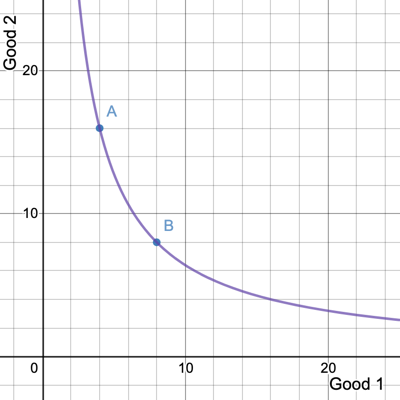
A

B

Do we have to take the
number of "utils" seriously?

From XKCD:

Just like the "volume" on an amp, "utils" are an arbitrary scale...saying you're "11" happy from a bundle doesn't mean anything!

All we want to use utility functions for
is to describe preference orderings.

It doesn't matter that “utils" are nonsense.

As long as the utility function generates the correct indifference map,
it doesn't matter what the level of utility at each indifference curve is.

Transforming Utility Functions

Applying a positive monotonic transformation to a utility function doesn't affect
the way it ranks bundles.

u(x_1,x_2) = x_1^{1 \over 2}x_2^{1 \over 2}
\hat u(x_1,x_2) = 2x_1^{1 \over 2}x_2^{1 \over 2}

Example: \(\hat u(x_1,x_2) = 2u(x_1,x_2)\)

u(4,16) = 8
u(9,4) = 6
u(4, 16) = 2 \times 8 = 16
u(9,4) = 2 \times 6 = 12

Transformations and the MRS

Applying a positive monotonic transformation to a utility function doesn't affect
its MRS at any bundle (and therefore generates the same indifference map).

u(x_1,x_2) = x_1^{1 \over 2}x_2^{1 \over 2}
\hat u(x_1,x_2) = 2x_1^{1 \over 2}x_2^{1 \over 2}
MU_1 = {1 \over 2}x_1^{-{1 \over 2}}x_2^{1 \over 2}
MU_2 = {1 \over 2}x_1^{{1 \over 2}}x_2^{-{1 \over 2}}
MU_1 = x_1^{-{1 \over 2}}x_2^{1 \over 2}
MU_2 = x_1^{{1 \over 2}}x_2^{-{1 \over 2}}
MRS =
\displaystyle{= {x_2 \over x_1}}
\hat{MRS} =
\displaystyle{= {x_2 \over x_1}}

Example: \(\hat u(x_1,x_2) = 2u(x_1,x_2)\)

Transformations and the MRS

Applying a positive monotonic transformation to a utility function doesn't affect
its MRS at any bundle (and therefore generates the same indifference map).

u(x_1,x_2) = x_1^{1 \over 2}x_2^{1 \over 2}
\hat u(x_1,x_2) = {1 \over 2}\ln x_1 + {1 \over 2}\ln x_2
MU_1 = {1 \over 2}x_1^{-{1 \over 2}}x_2^{1 \over 2}
MU_2 = {1 \over 2}x_1^{{1 \over 2}}x_2^{-{1 \over 2}}
MU_1 = {1 \over 2x_1}
MU_2 = {1 \over 2x_2}
MRS =
\displaystyle{= {x_2 \over x_1}}
\hat{MRS} =
\displaystyle{= {x_2 \over x_1}}

Example: \(\hat u(x_1,x_2) = \ln(u(x_1,x_2))\)

pollev.com/chrismakler

The utility function \(u(x_1,x_2) = x_1x_2^2\)​ represents the same preferences as which of the following utility functions? You may select more than one answer.