pollev.com/chrismakler

When is the first homework due?
Characteristics of
Production Functions
Christopher Makler
Stanford University Department of Economics
Econ 50: Lecture 3
Goal for Today: Analyze how different functional forms can be used to model different production processes


Examples of Production Functions
Linear
Leontief
(Fixed Proportions)
Cobb-Douglas
Constant Elasticity of Substitution (CES)
Story
If Chuck uses his bare hands (L), he can catch 2 fish per hour.
If Chuck uses a net (K),
he can collect 4 fish per net.
Model
Fish from L hours of labor = 2L
Fish from K nets = 4K
How many fish can he produce altogether if he uses
L hours of labor, and K nets?
If Chuck uses his bare hands (L), he can catch 2 fish per hour.
If Chuck uses a net (K),
he can collect 4 fish per net.
Intuition: no matter how many hours he works, and how many nets he uses,
he can catch the same number of fish with 1 net as he can using 2 hours of labor.
If Chuck uses his bare hands (L), he can catch 2 fish per hour.
If Chuck uses a net (K),
he can collect 4 fish per net.
What does an isoquant look like?
What does the isoquant for \(q = 20\) look like?
L
K
Linear Production Function
Linear Production Function
What happens to an isoquant if \(a\) increases?
L
K
Story
Two workers and a garbage truck can collect 16 bins per hour.
Adding a worker or getting an extra truck doesn't help.
Model
However, if you get another truck and two more workers, you can collect another 16 bins.
If you have more than twice as many workers as trucks,
your production depends on the number of trucks you have.
If you have less than twice as many workers as trucks,
your production depends on the number of workers you have.
If you have more than twice as many workers as trucks,
your production depends on the number of trucks you have.
If you have less than twice as many workers as trucks,
your production depends on the number of workers you have.
Leontief Production Function
What do the isoquants look like?
L
K
Leontief (Fixed Proportions) Production Function
Cobb-Douglas Production Function
Cobb-Douglas Production Function
What does the isoquant for \(q = 4\) look like?
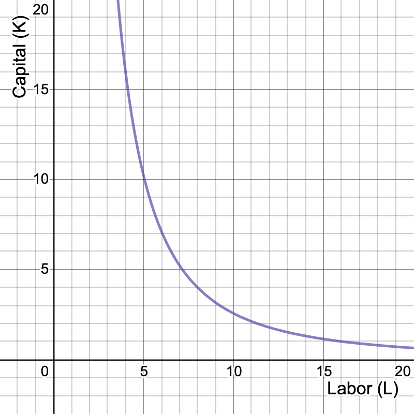
CES Production Function
MRTS for Different Production Functions
Linear
Leontief
(Fixed Proportions)
Cobb-Douglas
CES
Elasticity of Substitution
- Measures the substitutability of one input for another
- Key to answering the question: "will my job be automated?"
- Formal definition: the inverse of the percentage change in the MRTS
per percentage change in the ratio of capital to labor, K/L - Intuitively: how "curved" are the isoquants for a production function?
Scaling Production
How does a technology respond to increasing production?
Short run: only some resources can be reallocated
Long run: all resources can be reallocated
It depends on the time horizon:
Scaling Production in the Short Run
Suppose \(K\) is fixed at some \(\overline K\) in the short run.
Then the production function becomes \(f(L\ |\ \overline K)\)
pollev.com/chrismakler

When does the production function
exhibit diminishing marginal product of labor?
Scaling Production in the Long Run
What happens when we increase all inputs proportionally?
For example, what happens if we double both labor and capital?
Does doubling inputs -- i.e., getting \(f(2L,2K)\) -- double output?
Decreasing Returns to Scale
Constant Returns to Scale
Increasing Returns to Scale
Does this exhibit diminishing, constant or increasing MPL?
Does this exhibit decreasing, constant or increasing returns to scale?
pollev.com/chrismakler

When does the production function
exhibit constant returns to scale?
Next Steps
- Homework for today's class is due on Saturday night
- Readings and quizzes for next week have been posted
- Homework for next week will be posted later today