pollev.com/chrismakler

Today's Attendance Question

What is the color of the shirt I'm wearing?

The Implicit Function Theorem: Mathematical Derivation and Economic Interpretations

Christopher Makler

Stanford University Department of Economics

Econ 50: Lecture 6

General Function
(lecture 3)

Isoquant
(lecture 4)

PPF
(lecture 5)

f(x,y) = k
f(L,K) = q
L(x_1,x_2) = \overline L

Level Set

Magnitude of the slope of the level set

{\partial f(x,y)/\partial x \over \partial f(x,y)/\partial y}
{MP_L \over MP_K}
{\partial L(x_1,x_2)/\partial x_1 \over \partial L(x_1,x_2)/\partial x_2}

MRTS

MRT

Today's agenda: establish the intuition behind these formulas.

\text{Level set for }z=\{(x,y)|f(x,y)=z\}
\displaystyle{{\partial f \over \partial x} = \lim_{\Delta x \rightarrow 0} {f(x + \Delta x, y) - f(x, y) \over \Delta x}}
\displaystyle{{\partial f \over \partial y} = \lim_{\Delta y \rightarrow 0} {f(x, y + \Delta y) - f(x, y) \over \Delta y}}

Multivariable Chain Rule

\text{Example: }h(x,y)=(3x+y)^2
h(x,y)=f(g(x,y))
{\partial h \over \partial x} = {df \over dg} \times {\partial g \over \partial x}
f(g)=g^2
g(x)=3x+y

Total Derivative Along a Path

\text{How does }f(x,y)\text{ change along a path?}
\Delta f \approx
\displaystyle{{\partial f \over \partial x} \times \Delta x}
\displaystyle{{\partial f \over \partial y} \times \Delta y}
+
\text{Suppose the path is defined by some function }y(x):
\Delta f \approx
\displaystyle{{\partial f \over \partial x} \times \Delta x}
\displaystyle{{\partial f \over \partial y}}
+
\displaystyle{\times {dy \over dx}}
\displaystyle{\times \Delta x}
\displaystyle{\Delta f \over \Delta x} \approx
\displaystyle{{\partial f \over \partial x}}
\displaystyle{{\partial f \over \partial y}}
+
\displaystyle{\times {dy \over dx}}

Total Derivative Along a Path

\displaystyle{\Delta f \over \Delta x}\ \ \ \ \ \ \approx
\displaystyle{{\partial f \over \partial x}}
\displaystyle{{\partial f \over \partial y}}
+
\displaystyle{\times\ \ \ \ \ \ {dy \over dx}}

The total change in the height of the function due to a small increase in \(x\)

The amount \(f\) changes due to the increase in \(x\)

[indirect effect through \(y\)]

The amount \(f\) changes due to an increase in \(y\)

The amount \(y\) changes due to an increase in \(x\)

[direct effect from \(x\)]

y(x)=4-0.4x

Derivative Along a Level Set

f(x,y)=z

Take total derivative of both sides with respect to x:

Solve for \(dy/dx\):

\displaystyle{{\partial f \over \partial x}}
\displaystyle{{\partial f \over \partial y}}
+
\displaystyle{\times \ \ {dy \over dx}}
=
0
\displaystyle{{dy \over dx}}
= -
\displaystyle{{\partial f \over \partial x}}
\displaystyle{{\partial f \over \partial y}}

IMPLICIT FUNCTION THEOREM

pollev.com/chrismakler

Consider the multivariable function

f(x,y) = 4x^{1 \over 2}y

What is the slope of the level set passing through the point (1, 5)?

Consider the multivariable function

f(x,y) = 4x^{1 \over 2}y

What is the slope of the level set passing through the point (1, 5)?

\displaystyle{{\partial f(x,y) \over \partial x}=}
\displaystyle{{\partial f(x,y) \over \partial y}=}

Slope of level set =   —

Marginal Rate of Technical Substitution (MRTS)

Economic definition: the rate at which a producer can substitute one input for another while keeping output at the same level

Mathematical definition: slope of an isoquant

Recall: by implicit function theorem,
the slope of a level set is given by

\displaystyle{MRTS = {MP_L \over MP_K}}
\displaystyle{\left.{dy \over dx} \right|_{f(x,y) = z} = -{\partial f/\partial x \over \partial f/\partial y}}

Therefore the formula for the MRTS is

(absolute value)

Labor (L)

Capital (K)

Intuition behind the formula for the MRTS

Example: Cobb-Douglas Production Function

q=f(L,K)=AL^aK^b
MP_L = aAL^{a-1}K^b
MP_K = bAL^aK^{b-1}
MRTS =
\displaystyle{= {a \over b} \times {K \over L}}

Story

f(L,K) = 2L + 4K

If Chuck uses his bare hands (L), he can catch 2 fish per hour.

If Chuck uses a net (K),
he can collect 4 fish per net.

Model

Fish from L hours of labor = 2L

Fish from K nets = 4K

How many fish can he produce altogether if he uses
L hours of labor, and K nets?

f(L,K) = 2L + 4K

If Chuck uses his bare hands (L), he can catch 2 fish per hour.

If Chuck uses a net (K),
he can collect 4 fish per net.

MP_L = {df \over dL} = 2 {\text{fish} \over \text{hour}}
MP_K = {df \over dK} = 4 {\text{fish} \over \text{net}}
MRTS =
= {\text{1 net} \over \text{2 hours}}

Intuition: no matter how many hours he works, and how many nets he uses,
he can catch the same number of fish with 1 net as he can using 2 hours of labor.

Linear Production Function

MP_L =
MP_K =
MRTS =
\displaystyle{a\ {\text{output} \over \text{unit of L}}}
\displaystyle{b\ {\text{output} \over \text{unit of K}}}
\displaystyle{= {a \text{ units of K} \over b \text{ units of L}}}
q=f(L,K)=aL + bK

Linear Production Function

\displaystyle{MRTS = {a \text{ units of K} \over b \text{ units of L}}}
q=f(L,K)=aL + bK

What happens to an isoquant if \(a\) increases?

L

K

Cobb-Douglas Production Function

q=f(L,K)=AL^aK^b
MP_L = aAL^{a-1}K^b
MP_K = bAL^aK^{b-1}
MRTS =
\displaystyle{= {a \over b} \times {K \over L}}

Cobb-Douglas Production Function

q=f(L,K)=L^{1\over 2}K^{1 \over 4}

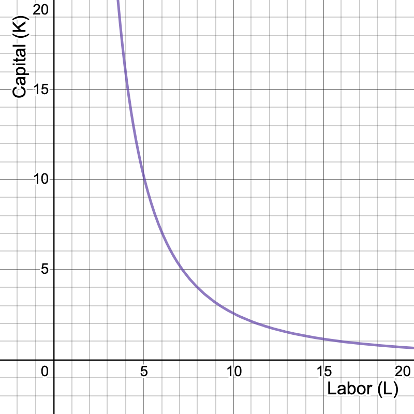
What does the isoquant for \(q = 4\) look like?

MRTS = {2K \over L}

CES Production Function

q=f(L,K)=(aL^\rho + bK^\rho)^{1 \over \rho}
\displaystyle{MRTS= {a \over b} \times \left({K \over L}\right)^{1-\rho}}

MRTS for Different Production Functions

aL + bK

Linear

Cobb-Douglas

AL^aK^b

CES

(aL^\rho + bK^\rho)^{1 \over \rho}
f(L,K)
MRTS(L,K)
\frac{a}{b}
\frac{a}{b}\times \frac{K}{L}
\frac{a}{b}\times \left(\frac{K}{L}\right)^{1-\rho}

NOTE THAT THESE ARE FUNCTIONS OF L AND K, NOT JUST OF L!!!

 

DO NOT CONVERT INTO A UNIVARIATE FUNCTION AND TAKE THE DERIVATIVE!!!

Slope of the PPF:
Marginal Rate of Transformation (MRT)

Rate at which one good may be “transformed" into another

...by reallocating resources from one to the other.

Opportunity cost of producing an additional unit of good 1,
in terms of good 2

Note: as with the MRTS, we will generally treat this as a positive number
(the magnitude of the slope)

This is just a level set of the function \(L(x_1,x_2) = {1 \over 3}x_1 + {1 \over 2}x_2\)

By the implicit function theorem:

\displaystyle{\text{slope of the level set}=-{{\partial L \over \partial x_1} \over {\partial L \over \partial x_2}}}
\displaystyle{=-{{1 \over 3} \over {1 \over 2}}}
\displaystyle{=-{2 \over 3}}
\displaystyle{\Rightarrow MRT ={2 \over 3}}

This is just a level set of the function \(L(x_1,x_2) = \)

By the implicit function theorem:

\displaystyle{\text{slope of the level set}=-{{dL_1 \over dx_1} \over {dL_2 \over dx_2}}}
\displaystyle{=-{{1 \over MP_{L1}} \over {1 \over {MP_{L2}}}}}
\displaystyle{=-{MP_{L2} \over MP_{L1}}}

Total labor required to produce the bundle \((x_1,x_2)\)

\(L_1(x_1) + L_2(x_2)\)

\({1 \over 3}x_1 + {1 \over 2}x_2\)

Recall: \(MP_{L1} = {dx_1 \over dL_1}, MP_{L2} = {dx_2 \over dL_2}\)

\displaystyle{\text{slope of the level set}=-{{\partial L \over \partial x_1} \over {\partial L \over \partial x_2}}}

Suppose we're allocating 100 units of labor to fish (good 1),
and 50 of labor to coconuts (good 2).

Now suppose we shift
one unit of labor
from coconuts to fish.

How many fish do we gain?

\Delta_2
\Delta_1

100

98

300

303

How many coconuts do we lose?

\Delta_2 = MP_{L_2} = 2\text{ coconuts}
\Delta_1 = MP_{L_1} = 3\text{ fish}
\left|\text{slope}\right| = \frac{MP_{L_2}}{MP_{L_1}}

Relationship between MPL's and MRT

x_1 = f_1(L_1) = 3L_1
x_2 = f_2(L_2) = 2L_2

Fish production function

Coconut production function

Resource Constraint

L_1 + L_2 = 150

PPF

Diminishing \(MP_L\)'s
and Increasing \(MRT\)

This is a level set of the function \(f(x_1,x_2) = {1 \over 100}x_1^2 + {1 \over 36}x_2^2\)

By the implicit function theorem:

\displaystyle{\text{slope of the level set}=-{{\partial f \over \partial x_1} \over {\partial f \over \partial x_2}}}
\displaystyle{=-{{2 \over 100}x_1 \over {2 \over 36}x_2}}
\displaystyle{=-{9x_1 \over 25x_2}}
\displaystyle{\Rightarrow MRT ={9x_1 \over 25x_2}}

Important Notes

The MRT is the slope of the PPF at some output combination \((x_1,x_2)\)

You should therefore write it in terms of \(x_1\) and \(x_2\), not \(L_1\) and \(L_2\).

Even though we show the relationship between the MRT and the MPL's, in general you should use the implicit function theorem to find it!

CHECK YOUR UNDERSTANDING

pollev.com/chrismakler

Charlene has the PPF given by
\(2x_1^3 + 3x_2^4 = 1072\)

 

What is her MRT if she produces the output combination \((8,2)\)?

\displaystyle{MRT = {{\partial f \over \partial x_1} \over {\partial f \over \partial x_2}}}
\displaystyle{= {6x_1^2 \over 12x_2^3}}

Since \(x_1^2 = 64\) and \(x_2^3 = 8\), this is 4.

By the implicit function theorem:

\displaystyle{= {x_1^2 \over 2x_2^3}}

DO NOT SOLVE FOR X2 AS A FUNCTION OF X1 AND TAKE THE DERIVATIVE!!!!

  • The implicit function theorem is a general mathematical theorem giving the slope of a level set at a point.
  • We applied this function today in two contexts.
  • Remember what the units of the axes are!!!! That determines the variables you should use in describing the slope, as well as the units of the slope!
  • DO NOT JUST CONVERT TO A UNIVARIATE FUNCTION.
    THIS WILL LEAD YOU DOWN A BAD PATH AND
    YOU WILL GET MANY MANY POINTS OFF ON EXAMS.

Key Takeaways