pollev.com/chrismakler

Tell me something good.

Technology and
Production Functions

Christopher Makler

Stanford University Department of Economics

Econ 50: Lecture 4

Lecture 2: Production Functions

Labor

Fish

🐟

Capital

Coconuts

🥥

[GOODS]

⏳

⛏

[RESOURCES]

Unit I: Scarcity and Choice

Economics is the study of how
we use scarce resources 
to satisfy our unlimited wants

Resources

Goods

Happiness

🌎

⌚️

🤓

Production Functions

A mathematical form describing how much output is produced as a function of inputs.

Labor \((L)\)

Capital \((K)\)

Production Function  \(f(L,K)\)

Output (\(q\) or \(x\))

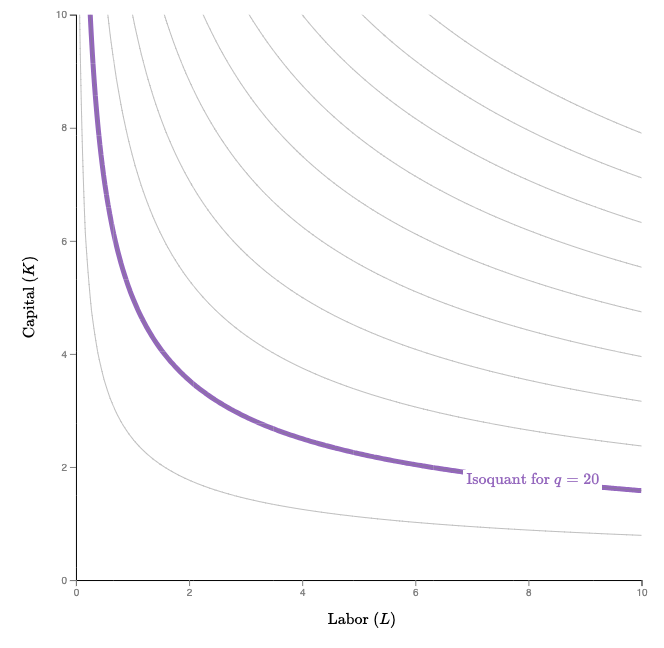
Isoquants

Economic definition: if you want to produce some amount \(q\) of output, what combinations of inputs could you use?

Mathematical definition:
level sets of the production function

\text{Isoquant for }q = \{(L,K)\ |\ f(L,K) = q\}

Isoquant: combinations of inputs that produce a given level of output

Isoquant map: a contour map showing the isoquants for various levels of output

pollev.com/chrismakler

What happens to isoquants after an improvement in technology?

Marginal Products of Labor and Capital

Economic definition: how much more output is produced if you increase labor or capital?

Mathematical definition:
partial derivatives of the production function

\displaystyle{MP_L = {\partial f(L,K) \over \partial L}}

These are both rates: they are measured in terms of units of ouptut per unit of input.

\displaystyle{= \lim_{\Delta L \rightarrow 0} {f(L + \Delta L, K) - f(L, K) \over \Delta L}}
\displaystyle{MP_K = {\partial f(L,K) \over \partial K}}
\displaystyle{=\lim_{\Delta K \rightarrow 0} {f(L, K + \Delta K) - f(L, K) \over \Delta K}}

pollev.com/chrismakler

Consider the production function

f(L,K) = 4L^{1 \over 2}K

What is the expression for the marginal product of labor?

Marginal Rate of Technical Substitution (MRTS)

Economic definition:
the rate at which a producer
can substitute one input for another
while keeping output at the same level

Visual definition:
slope of an isoquant

Mathematical definition:
we'll get to this in section and on Friday

Functional Forms

How can different functional forms can be used to model different production processes?

Examples of Production Functions

f(L,K) = aL + bK

Linear

f(L,K) = \min\{aL, bK\}

Leontief
(Fixed Proportions)

Cobb-Douglas

f(L,K) = AL^aK^b

Constant Elasticity of Substitution (CES)

f(L,K) = (aL^\rho + bK^\rho)^{1 \over \rho}

[50Q only]

Story

f(L,K) = 2L + 4K

If Chuck uses his bare hands (L), he can catch 2 fish per hour.

If Chuck uses a net (K),
he can collect 4 fish per net.

Model

Fish from L hours of labor = 2L

Fish from K nets = 4K

How many fish can he produce altogether if he uses
L hours of labor, and K nets?

MP_L =
MP_K =
2
4

Cobb-Douglas Production Function

q=f(L,K)=AL^aK^b
MP_L = aAL^{a-1}K^b
MP_K = bAL^aK^{b-1}

What story do these marginal products tell us?

When do these functions have diminishing marginal products?

Three Ways to Think About Production

(C) Returns to scale:

keep \(K/L\) constant,

increase \(q\) by scaling up

both labor and capital

(A)

(A) Elasticity of substitution:

keep \(q\) constant,

move along an isoquant

(B)

(B)  Short run production function:

keep \(K\) constant,

increase \(q\) by adding labor

(C)

Elasticity of Substitution

  • Measures the substitutability of one input for another
  • Key to answering the question: "will my job be automated?"
  • Formal definition: the inverse of the percentage change in the MRTS 
    per percentage change in the ratio of capital to labor, K/L
  • Intuitively: how "curved" are the isoquants for a production function?

CES Production Function

q=f(L,K)=(aL^\rho + bK^\rho)^{1 \over \rho}

Scaling Production

How does a technology respond to increasing production?

Short run: only some resources can be reallocated

Long run: all resources can be reallocated

It depends on the time horizon:

Scaling Production in the Short Run

Suppose \(K\) is fixed at some \(\overline K\) in the short run.
Then the production function becomes \(f(L\ |\ \overline K)\)

pollev.com/chrismakler

When does the production function

f(L) = 10L^a

exhibit diminishing marginal product of labor?

Scaling Production in the Long Run

What happens when we increase all inputs proportionally?

For example, what happens if we double both labor and capital?

Does doubling inputs -- i.e., getting \(f(2L,2K)\) -- double output?

f(2L,2K) > 2f(L,K)
f(2L,2K) = 2f(L,K)
f(2L,2K) < 2f(L,K)

Decreasing Returns to Scale

Constant Returns to Scale

Increasing Returns to Scale

f(L,K) = 4L^{1 \over 2}K

Does this exhibit diminishing, constant or increasing MPL?

Does this exhibit decreasing, constant or increasing returns to scale?

pollev.com/chrismakler

When does the production function

f(L,K) = AL^aK^b

exhibit constant returns to scale?

f(L,K) = AL^aK^b
f(2L,2K) = A(2L)^a(2K)^b
=2^a2^bAL^aK^b
=2^{a+b}AL^aK^b
=2^{a+b}f(L,K)

How does this compare to \(2f(L,K)\)?

In other words, does this represent double the output,
more than double the output, or less than double the output produced by \((L,K)\)?

f(L,K) = AL^aK^b

Scaling and the Cobb-Douglas production function

The exponent \(a\) determines if the \(MP_L\) is diminishing, constant, or increasing

The exponent \(b\) determines if the \(MP_K\) is diminishing, constant, or increasing

The sum of the exponents \(a + b\) determines if \(f(L,K)\) exhibits
 decreasing, constant, or increasing returns to scale

Summary

So far we've modeled an important economic activity
using multivariable calculus.

We looked at the economic meaning for
various properties of the production function:

Partial Derivatives

Marginal Products

Level Sets

Isoquants

Slope of a Level Set

Marginal Rate of Technical Substitution

In section and on Friday, we'll analyze how
to derivate the slope of an isoquant (MRTS) and a PPF (MRT).

Next time, we'll look at production possibilities for two goods using a PPF model.