Analyzing a Price Change

Christopher Makler

Stanford University Department of Economics

Econ 50: Lecture 14

Part I: Income and Substitution Effects

Break down overall effect
of a price change
into its component parts

How much does a price increase
hurt a consumer?

Part II: Welfare Analysis

More broadly: what is the relationship between money and utility?

Today's Agenda

Today's Agenda

Part 1: Income and Substitution Effects

Part 2: Welfare Analysis

Decomposing the effects of a price change

Finding the decomposition bundle

Income and substitution effects

Complements and Substitute

Relationship between utility & money

Compensating variation

Equivalent variation

Consumer's Surplus

 

Demand function: how does an optimal bundle change when prices or income changes?

If we want to know how best to implement a policy, we want to know why it changes.

For example: we could be interested in how far a cannonball travels, so we can aim it at a target.

To do this, a physicist would decompose its velocity
into the horizontal portion and vertical portion:

Two Effects

Substitution Effect

Effect of change in relative prices, holding utility constant.

Effect of change in real income,
holding relative prices constant.

Income Effect

Decomposition Bundle

Suppose that, after a price change,
we compensated the consumer
just enough to afford some bundle
that would give the same utility
as they had before the price change?

The Hicks decomposition bundle
is the lowest-cost bundle
that satisfies this condition.

Approach

TOTAL EFFECT

A
C
B

INITIAL BUNDLE

FINAL BUNDLE

DECOMPOSITION BUNDLE

SUBSTITUTION EFFECT

INCOME  EFFECT

Income Offer Curve

Price Offer Curve
for a Good

Review: Offer Curves

Holding the prices of both goods constant,
show how the optimal bundle changes
as the consumer's income changes.

Holding the price of the other good
and consumer's income constant,
show how the optimal bundle changes
as the price of this good changes.

Offer curves are plotted in Good 1 - Good 2 space (along with budget lines and indifference curves)

pollev.com/chrismakler

A change in the price of good 1 will result in a ______ the price offer curve for good 1
and a ______ the income offer curve.

TOTAL EFFECT

A
C
B

INITIAL BUNDLE

FINAL BUNDLE

DECOMPOSITION BUNDLE

SUBSTITUTION EFFECT

INCOME  EFFECT

Movement along POC

Shift of IOC

Movement along IOC

Hicks Decomposition

Hicks Decomposition Bundle

Suppose the price of good 1 increases from \(p_1\) to \(p_1^\prime\).

The price of good 2 (\(p_2\)) and income (\(m\)) remain unchanged.

Initial Bundle (A):
Solves
utility maximization
problem

Final Bundle (C):
Solves
utility maximization
problem

\max \ u(x_1,x_2)
\min \ p_1^\prime x_1 + p_2x_2
\text{s.t. }p_1x_1 + p_2x_2 = m
\text{s.t. }u(x_1,x_2) = U(A)

Decomposition Bundle (B):
Solves
cost minimization
problem

\max \ u(x_1,x_2)
\text{s.t. }p_1^\prime x_1 + p_2x_2 = m

"Compensated Budget Line"

The "compenated budget line" shows the budget line as if the consumer was given just enough money to achieve their initial utility at the new prices.

A consumer's compensated budget line:

"Compensated Budget Line"

If a consumer's preferences are well behaved, her compensated budget line

might lie below bundle A,
or pass through A, but cannot lie above A.

"Compensated Budget Line"

If a consumer's preferences are well behaved, her compensated budget line

might lie below bundle A,
or pass through A, but cannot lie above A.

Why? Because A could still be the cost-minimizing bundle, even at the new prices. But a budget line that passed above A
could not find the cost-minimizing bundle, because A would be cheaper! 

In this example, \(p1\) and \(p_1\) started at 2 each, and then \(p_1\) rose to 8.

How would the diagram have been different if \(p_2\) had fallen to 0.5 instead?

pollev.com/chrismakler

In this example,
C was below and to the left of B.

What does that say about whether goods 1 and 2 are normal or inferior?

pollev.com/chrismakler

Complements and Substitutes (one last time)

Complements

Substitutes

When the price of good 1 goes up...

Net effect: buy less of both goods

Net effect: buy less good 1 and more good 2

Substitution effect: buy less of good 1 and more of good 2

Income effect (if both goods normal): buy less of both goods

Substitution effect dominates

Income effect dominates

= \begin{cases}\infty & \text{ if } x_1 < x_2 \\ 0 & \text{ if } x_1 > x_2 \end{cases}
-\infty
1
0
MRS = \left(x_2 \over x_1\right)^\infty
MRS = {x_2 \over x_1}
MRS = 1
r
u(x_1,x_2) = \min\{x_1,x_2\}
u(x_1,x_2) = x_1x_2
u(x_1,x_2) = x_1 + x_2

PERFECT
SUBSTITUTES

PERFECT
COMPLEMENTS

INDEPENDENT

PERFECT
SUBSTITUTES

u(x_1,x_2) = (x_1^r+x_2^r)^{1 \over r}

Constant Elasticity of Substitution (CES) Utility

MRS = \left(x_2 \over x_1\right)^{1-r}
u(x_1,x_2) = (x_1^r+x_2^r)^{1 \over r}

Constant Elasticity of Substitution (CES) Utility

MRS = \left(x_2 \over x_1\right)^{1-r}
-\infty
1
r

COMPLEMENTS: \(r < 0\)

SUBSTITUTES: \(r > 0\)

-1
MRS = \left(x_2 \over x_1\right)^2
{1 \over 2}
MRS = \left(x_2 \over x_1\right)^{1 \over 2}
u(x_1,x_2) = (x_1^{-1}+x_2^{-1})^{-1}
u(x_1,x_2) = \left(x_1^{1 \over 2} + x_2^{1 \over 2}\right)^2

Which of the following would be true if these goods were substitutes rather than complements?

pollev.com/chrismakler

Note: whether the goods are complements or substitutes has to do with the income and substitution effects on the good whose price has not changed.

 

(It's about how much you change your buying habits due to the change in another good.)

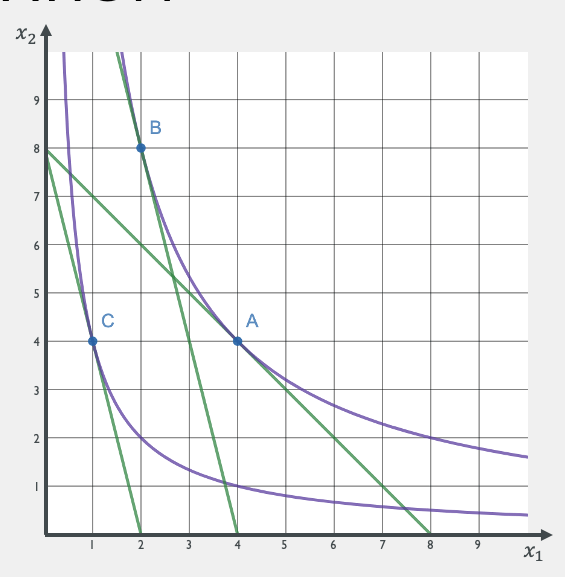
Hicks Decomposition: Worked Example

Hicks Decomposition Bundle

You have the utility function \(u(x_1,x_2) = x_1^{1 \over 2}x_2^{1 \over 2}\).

Suppose the price of good 1 increases from \(p_1 = 1\) to \(p_1^\prime = 4\).

The price of good 2 and income remain unchanged at \(p_2 = 1\) and \(m = 8\).

Initial Bundle (A):
Solves
utility maximization
problem

Final Bundle (C):
Solves
utility maximization
problem

\max \ u(x_1,x_2)
\min \ p_1^\prime x_1 + p_2x_2
\text{s.t. }p_1x_1 + p_2x_2 = m
\text{s.t. }u(x_1,x_2) = U(A)

Decomposition Bundle (B):
Solves
cost minimization
problem

\max \ u(x_1,x_2)
\text{s.t. }p_1^\prime x_1 + p_2x_2 = m
\max \ x_1^{1 \over 2}x_2^{1 \over 2}
\text{s.t. }x_1 + x_2 = 8
\min \ 4x_1 + x_2
\text{s.t. }x_1^{1 \over 2}x_2^{1 \over 2} = U(A)
\max \ x_1^{1 \over 2}x_2^{1 \over 2}
\text{s.t. }4 x_1 + x_2 = 8

(A) Solves utility maximization problem

(C) Solves utility maximization problem

(B) Solves cost
minimization problem

\max \ x_1^{1 \over 2}x_2^{1 \over 2}
\text{s.t. }x_1 + x_2 = 8
\min \ 4x_1 + x_2
\text{s.t. }x_1^{1 \over 2}x_2^{1 \over 2} = U(A)
\max \ x_1^{1 \over 2}x_2^{1 \over 2}
\text{s.t. }4 x_1 + x_2 = 8

Tangency condition:

Tangency condition:

Tangency condition:

{x_2 \over x_1} = 1
{x_2 \over x_1} = 4

Tangency condition:

Tangency condition:

Constraint:

Constraint:

Constraint:

x_1 + x_2 = 8
4 x_1 + x_2 = 8
x_1 = x_2
x_2 = 4x_1
{x_2 \over x_1} = 4
x_2 = 4x_1

Bundle B:

Bundle A:

Bundle C:

x_1 + \ \ \ \ \ = 8
x_1
4x_1 + \ \ \ \ \ \ = 8
4x_1
x_1^* = 4
(4,4)
(2,8)
(1,4)
x_1^* = 1
x_1^{1 \over 2}x_2^{1 \over 2} = 4
u(A) = 4^{1 \over 2}4^{1 \over 2} = 4
\text{s.t. }x_1^{1 \over 2}x_2^{1 \over 2} = 4
x_1^{1 \over 2}[\ \ \ \ \ \ \ \ ]^{1 \over 2} = 4
4x_1
2x_1 = 4

Hicks Decomposition Bundle

You have the utility function \(u(x_1,x_2) = x_1^{1 \over 2}x_2^{1 \over 2}\).

Suppose the price of good 1 increases from \(p_1 = 1\) to \(p_1^\prime = 4\).

The price of good 2 and income remain unchanged at \(p_2 = 1\) and \(m = 8\).

Initial Bundle (A):
Solves
utility maximization
problem

Final Bundle (C):
Solves
utility maximization
problem

Decomposition Bundle (B):
Solves
cost minimization
problem

\max \ x_1^{1 \over 2}x_2^{1 \over 2}
\text{s.t. }x_1 + x_2 = 8
\min \ 4x_1 + x_2
\text{s.t. }x_1^{1 \over 2}x_2^{1 \over 2} = U(A)
\max \ x_1^{1 \over 2}x_2^{1 \over 2}
\text{s.t. }4 x_1 + x_2 = 8

Bundle B:

Bundle A:

Bundle C:

(4,4)
(2,8)
(1,4)

Hicks Decomposition Bundle

You have the utility function \(u(x_1,x_2) = x_1^{1 \over 2}x_2^{1 \over 2}\).

Suppose the price of good 1 increases from \(p_1 = 1\) to \(p_1^\prime = 4\).

The price of good 2 and income remain unchanged at \(p_2 = 1\) and \(m = 8\).

Initial Bundle (A): Solves utility maximization problem with the initial price

Final Bundle (C): Solves
utility maximization
problem with the new price

Decomposition Bundle (B):
Solves cost minimization
problem with the new price and initial utility

A=(4,4)
B=(2,8)
C=(1,4)