Using Consumer Theory to Analyze Policy Decisions

Christopher Makler

Stanford University Department of Economics

Econ 50: Lecture 16

Solving Climate Change in one Easy Step

Climate change is real and caused in large part by burning fossil fuels.
Transportation is a big part of the problem.
A higher tax on gasoline would make people drive less, and have many other benefits. See Mankiw's Pigou Club Manifesto.
Estimates vary, but $10/gallon seems about right.

but...

$10/gallon gas would hurt a lot of people, especially those with lower incomes who depend on a car to get to work

Can we give them a certain amount of money that would make them no worse off than they were before, to compensate them for the price increase?

Monday: Income and Substitution Effects

Break down overall effect
of a price change
into its component parts

How much does a price increase
hurt a consumer?

Today: Policy Analysis

How much utility can you buy with a certain amount of money?

How much money does a certain amount of utility cost?

This Week

Wednesday: Relationship between Money and Utility

How can we use policies that affect prices and income to improve outcomes?

Two Effects

Substitution Effect

Effect of change in relative prices, holding utility constant.

Effect of change in real income,
holding relative prices constant.

Income Effect

Decomposition Bundle

Suppose that, after a price change,
we compensated the consumer
just enough to afford some bundle
that would give the same utility
as they had before the price change?

The Hicks decomposition bundle
is the lowest-cost bundle
that satisfies this condition.

Approach

TOTAL EFFECT

INITIAL BUNDLE

FINAL BUNDLE

DECOMPOSITION BUNDLE

SUBSTITUTION EFFECT

INCOME EFFECT

Income Offer Curve

Price Offer Curve
for a Good

Review: Offer Curves

Holding the prices of both goods constant,
show how the optimal bundle changes
as the consumer's income changes.

Holding the price of the other good
and consumer's income constant,
show how the optimal bundle changes
as the price of this good changes.

Offer curves are plotted in Good 1 - Good 2 space (along with budget lines and indifference curves)

pollev.com/chrismakler

A change in the price of good 1 will result in a ______ the price offer curve for good 1
and a ______ the income offer curve.

TOTAL EFFECT

INITIAL BUNDLE

FINAL BUNDLE

DECOMPOSITION BUNDLE

SUBSTITUTION EFFECT

INCOME EFFECT

Movement along POC

Shift of IOC

Movement along IOC

Hicks Decomposition

Hicks Decomposition Bundle

Suppose the price of good 1 increases from $p_1$ to $p_1^\prime$.

The price of good 2 ($p_2$) and income ($m$) remain unchanged.

Initial Bundle (A):
Solves
utility maximization
problem

Final Bundle (C):
Solves
utility maximization
problem

\max \ u(x_1,x_2)

\min \ p_1^\prime x_1 + p_2x_2

\text{s.t. }p_1x_1 + p_2x_2 = m

\text{s.t. }u(x_1,x_2) = U(A)

Decomposition Bundle (B):
Solves
cost minimization
problem

\max \ u(x_1,x_2)

\text{s.t. }p_1^\prime x_1 + p_2x_2 = m

"Compensated Budget Line"

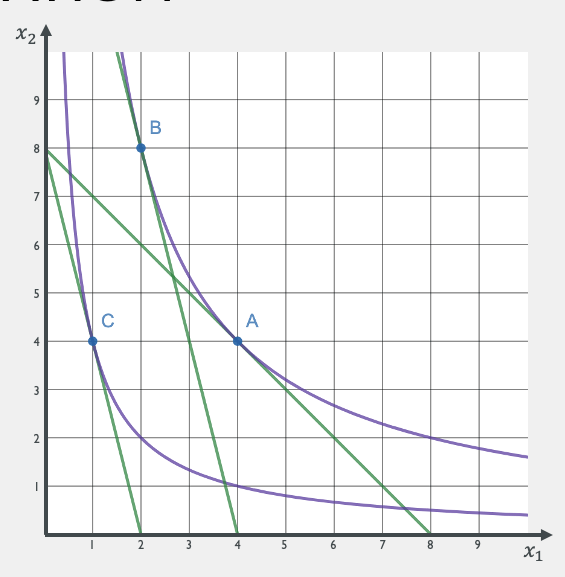
In this example, $p1$ and $p_1$ started at 2 each, and then $p_1$ rose to 8.

How would the diagram have been different if $p_2$ had fallen to 0.5 instead?

pollev.com/chrismakler

In this example,
C was below and to the left of B.

What does that say about whether goods 1 and 2 are normal or inferior?

pollev.com/chrismakler

Hicks Decomposition: Worked Example

Hicks Decomposition Bundle

You have the utility function $u(x_1,x_2) = x_1^{1 \over 2}x_2^{1 \over 2}$.

Suppose the price of good 1 increases from $p_1 = 1$ to $p_1^\prime = 4$.

The price of good 2 and income remain unchanged at $p_2 = 1$ and $m = 8$.

Initial Bundle (A):
Solves
utility maximization
problem

Final Bundle (C):
Solves
utility maximization
problem

\max \ u(x_1,x_2)

\min \ p_1^\prime x_1 + p_2x_2

\text{s.t. }p_1x_1 + p_2x_2 = m

\text{s.t. }u(x_1,x_2) = U(A)

Decomposition Bundle (B):
Solves
cost minimization
problem

\max \ u(x_1,x_2)

\text{s.t. }p_1^\prime x_1 + p_2x_2 = m

\max \ x_1^{1 \over 2}x_2^{1 \over 2}

\text{s.t. }x_1 + x_2 = 8

\min \ 4x_1 + x_2

\text{s.t. }x_1^{1 \over 2}x_2^{1 \over 2} = U(A)

\max \ x_1^{1 \over 2}x_2^{1 \over 2}

\text{s.t. }4 x_1 + x_2 = 8

(A) Solves utility maximization problem

(B) Solves cost
minimization problem

\max \ x_1^{1 \over 2}x_2^{1 \over 2}

\text{s.t. }x_1 + x_2 = 8

\min \ 4x_1 + x_2

\text{s.t. }x_1^{1 \over 2}x_2^{1 \over 2} = U(A)

\max \ x_1^{1 \over 2}x_2^{1 \over 2}

\text{s.t. }4 x_1 + x_2 = 8

Tangency condition:

{x_2 \over x_1} = 1

{x_2 \over x_1} = 4

Tangency condition:

Constraint:

x_1 + x_2 = 8

4 x_1 + x_2 = 8

x_1 = x_2

x_2 = 4x_1

{x_2 \over x_1} = 4

x_2 = 4x_1

Bundle B:

Bundle A:

Bundle C:

x_1 + \ \ \ \ \ = 8

x_1

4x_1 + \ \ \ \ \ \ = 8

4x_1

x_1^* = 4

(4,4)

(2,8)

(1,4)

x_1^* = 1

x_1^{1 \over 2}x_2^{1 \over 2} = 4

u(A) = 4^{1 \over 2}4^{1 \over 2} = 4

\text{s.t. }x_1^{1 \over 2}x_2^{1 \over 2} = 4

x_1^{1 \over 2}[\ \ \ \ \ \ \ \ ]^{1 \over 2} = 4

4x_1

2x_1 = 4

Hicks Decomposition Bundle

You have the utility function $u(x_1,x_2) = x_1^{1 \over 2}x_2^{1 \over 2}$.

Suppose the price of good 1 increases from $p_1 = 1$ to $p_1^\prime = 4$.

The price of good 2 and income remain unchanged at $p_2 = 1$ and $m = 8$.

Initial Bundle (A):
Solves
utility maximization
problem

Final Bundle (C):
Solves
utility maximization
problem

Decomposition Bundle (B):
Solves
cost minimization
problem

\max \ x_1^{1 \over 2}x_2^{1 \over 2}

\text{s.t. }x_1 + x_2 = 8

\min \ 4x_1 + x_2

\text{s.t. }x_1^{1 \over 2}x_2^{1 \over 2} = U(A)

\max \ x_1^{1 \over 2}x_2^{1 \over 2}

\text{s.t. }4 x_1 + x_2 = 8

Bundle B:

Bundle A:

Bundle C:

(4,4)

(2,8)

(1,4)

Hicks Decomposition Bundle

You have the utility function $u(x_1,x_2) = x_1^{1 \over 2}x_2^{1 \over 2}$.

Suppose the price of good 1 increases from $p_1 = 1$ to $p_1^\prime = 4$.

The price of good 2 and income remain unchanged at $p_2 = 1$ and $m = 8$.

Initial Bundle (A): Solves utility maximization problem with the initial price

Final Bundle (C): Solves
utility maximization
problem with the new price

Decomposition Bundle (B):
Solves cost minimization
problem with the new price and initial utility

A=(4,4)

B=(2,8)

C=(1,4)

Welfare Effects of a Price Change

Link to PowerPoint deck

Consumer Theory Checklist

Budget line / budget set
Utility maximization
Demand curve
Price offer curve
Income offer curve
Hicks decomposition
Cost minimization

Graphs / Representations

Complements
Substitutes
Normal Goods
Inferior Goods
Income Effect
Substitution Effect
Compensating Variation
Equivalent Variation

Concepts

Utility-maximizing bundle given a budget constraint
Ordinary (Marshallian) demand function
Cost-minimizing bundle given a utility constraint
Compensated (Hicksian) demand function
Indirect utility function
Expenditure function

Derivations

You should be able to perform this kind of analysis for any utility function,
including ones you haven't seen before (or seen before in this context).

Next Week:
From Consumers to Firms

Monday: production and cost for a firm
Wednesday: elasticity and revenue
Friday: profit maximization
Following Monday (11/11): Midterm 2

Using Consumer Theory to Analyze Policy Decisions

Solving Climate Change in one Easy Step

but...

Monday: Income and Substitution Effects

Today: Policy Analysis

This Week

Wednesday: Relationship between Money and Utility

Two Effects

Substitution Effect

Income Effect

Decomposition Bundle

Approach

Income Offer Curve

Price Offer Curve for a Good

Review: Offer Curves

Hicks Decomposition

Hicks Decomposition Bundle

Hicks Decomposition: Worked Example

Hicks Decomposition Bundle

Hicks Decomposition Bundle

Hicks Decomposition Bundle

Welfare Effects of a Price Change

Consumer Theory Checklist

Next Week: From Consumers to Firms

Price Offer Curve
for a Good

Next Week:
From Consumers to Firms