Input and Output Decisions of a Competitive Firm
Christopher Makler
Stanford University Department of Economics
Econ 50 | Lecture 18
pollev.com/chrismakler

What determines how much someone is paid?
(In real life, not this course.)

Take everything we're about to do with a gigantic grain of salt.

Sunday
1-3pm SEA Study Hall Lathrop 282
3-5pm Review Session CODA B90
Theory of the Firm
Exogenous Variables
Endogenous Variables
technology, \(f(L,K)\)
level of output, \(q\)
input prices \(w, r\)
Cost Minimization
Profit Maximization
cost function, \(c(w,r,q)\)
revenue function \(r(q)\)
Special Case: Competitive Firm
Exogenous Variables
Endogenous Variables
technology, \(f(L,K)\)
level of output, \(q\)
input prices \(w, r\)
Cost Minimization
Profit Maximization
cost function, \(c(w,r,q)\)
market price \(p\)
Optimization
What is an agent's optimal behavior for a fixed set of circumstances?
Utility-maximizing bundle for a consumer
Profit-maximizing quantity for a firm
Profit-maximizing input choice for a firm
Comparative Statics
How does an agent's optimal behavior change when circumstances change?
Utility-maximizing bundle for a consumer
Profit-maximizing quantity for a firm
Profit-maximizing input choice for a firm
Assumptions
We will be analyzing a
competitive (price-taking) firm
in the short run
- output price \(p\)
- wage rate \(w\)
Last Time:
Profit Maximization
Optimize by taking derivative and setting equal to zero:
Profit is total revenue minus total costs:
"Marginal revenue equals marginal cost"
Example:
What is the profit-maximizing value of \(q\)?
Optimize by taking derivative and setting equal to zero:
Profit is total revenue minus total costs:
"Marginal revenue equals marginal cost"
Average Profit Analysis
Multiply right-hand side by \(q/q\):
Profit is total revenue minus total costs:
"Profit per unit times number of units"
AVERAGE PROFIT
Competitive (Price-Taking) Firms
Demand and Inverse Demand
Demand curve:
quantity as a function of price
Inverse demand curve:
price as a function of quantity
QUANTITY
PRICE
Special case: perfect substitutes
Demand and Inverse Demand
Demand curve:
quantity as a function of price
Inverse demand curve:
price as a function of quantity
QUANTITY
PRICE
Special case: perfect substitutes
For a small firm, it probably looks like this...
Price
MC
\(q\)
$/unit
P = MR
12
24
Output Supply as a Function of \(p\) with Fixed \(w\)
When price is fixed at 12
For a general price
1. Costs and Revenues
2. Profit = total revenues minus total costs
3. Take derivative of profit function, set =0
Profit-Maximizing Output Choice when \(w = 8\), \(r = 2\), and \(\overline K = 32\)
NUMBER
FUNCTION
TR
TC
MR
MC
Take derivative and set = 0:
Solve for \(q^*\):
SUPPLY FUNCTION

When \(p = 4\), this function says that the firm should produce \(q = 8\).
If it does this...
When \(p = 12 , w = 8, \overline K = 32\)
For a general \(p, w\), with \(r= 2, \overline K = 32\)
1. Costs and Revenues
2. Profit = total revenues minus total costs
3. Take derivative of profit function, set =0
Now's let's also let wage be a variable
NUMBER
FUNCTION
When \(p = 12 , w = 8, \overline K = 32\)
For a general \(p, w,r\) and \(\overline K\)
1. Costs and Revenues
2. Profit = total revenues minus total costs
3. Take derivative of profit function, set =0
Now's let's also let wage and capital be a variable
NUMBER
FUNCTION
Profit-Maximizing Demand for Labor
Three Approaches
- Plug \(q^*(p,w)\) into conditional labor demand \(L^c(q)\)
- Write profit as a function of labor, solve for optimal quantity of labor to hire
- Choose point along production function where the last worker's marginal product of labor is equal to their real wage.
PROFIT-MAXIMIZING
LABOR DEMAND FUNCTION
SUPPLY FUNCTION
the conditional labor demand
for the profit-maximizing supply:
The profit-maximizing labor demand is
CONDITIONAL LABOR DEMAND FUNCTION
TR
TC
MRPL
MC
Take derivative and set = 0:
Solve for \(L^*\):
PROFIT-MAXIMIZING
LABOR DEMAND FUNCTION
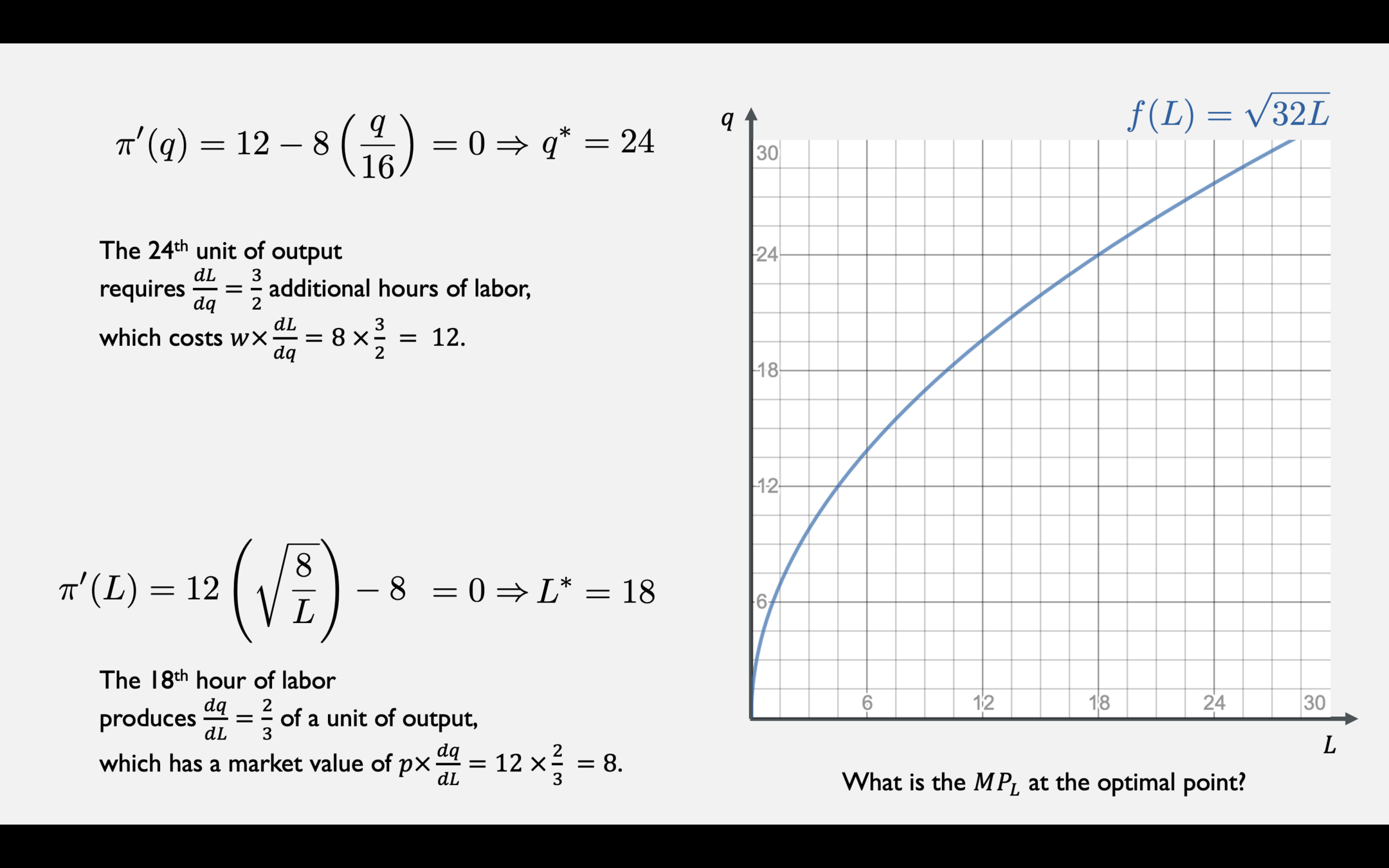
Profit as a function of output \(q\)
Profit as a function of labor \(L\)
1. Costs for general \(w\) and revenue for general \(p\)
2. Profit = total revenues minus total costs
3. Take derivative of profit function, set =0
PROFIT-MAXIMIZING OUTPUT SUPPLY
PROFIT-MAXIMIZING LABOR DEMAND
Profit as a function of output \(q\)
Profit as a function of labor \(L\)
1. Costs for general \(w\) and revenue for general \(p\)
2. Profit = total revenues minus total costs
3. Take derivative of profit function, set =0
[cost of labor required for \(q\) units of output]
[revenue of output produced by \(L\) hours of labor]
MARGINAL COST (MC)
MARGINAL REVENUE PRODUCT OF LABOR (MRPL)
"Keep producing output as long as the marginal revenue from the last unit produced is at least as great as the marginal cost of producing it."
"Keep hiring workers as long as the marginal revenue from the output of the last worker is at least as great as the cost of hiring them."
Profit as a function of output \(q\)
Profit as a function of labor \(L\)
Is it true?
Are people paid the value of their marginal product?
What determines the value of people's work?
What should?
What determines how much people are paid?
Sunday
1-3pm SEA Study Hall Lathrop 282
3-5pm Review Session CODA B90