A Competitive Firm's
Labor Demand

Christopher Makler

Stanford University Department of Economics

Econ 50 | Lecture 21

We'll stick with our same function

f(L,K) = \sqrt{LK}
\overline K = 32
L(q) = {q^2 \over K}
MP_L = \frac{1}{2}\sqrt{K \over L}
L(q) = {q^2 \over 32}
MP_L = \sqrt{8 \over L}
f(L) = \sqrt{32L}

This Week's Agenda

Review of firm profit maximization, with and without market power

Edge cases

Deriving output supply
as a function of \(p\),
holding \(w\) constant

Deriving labor demand
as a function of \(w\),
holding \(p\) constant

Analyzing how a change in \(w\)
shifts the supply curve

Analyzing how a change in \(p\)
shifts the labor demand curve

[ MOVEMENT
ALONG CURVES]

[ SHIFTS OF
 CURVES]

Wednesday

Friday

Are people paid their marginal value?

c(q) = 64 + {1 \over 4}q^2
r(q) = pq = 12q
\text{Let's assume }p = 12:
\text{Profit function is:}
\text{Total cost}
\pi(q) = 12q - [64 + {1 \over 4}q^2]
\text{Take derivative with respect to } q \text{ and set equal to zero:}
\pi'(q) = \ \ \ \ \ \ - \ \ \ \ \ \ = 0
12
{1 \over 2}q

Price

MC

\(q\)

$/unit

P = MR

12

MC = {1 \over 2}q

24

\Rightarrow q^* = 24

Key insight for today: the profit-maximizing choice of \(q\) is also a profit-maximizing choice of \(L\).

\pi = pq - (wL + rK)

The production function tells us the relationship between labor and output:

q = f(L)
L = L^c(q)
q = \sqrt{L \overline K}
L = {q^2 \over \overline K}

Profit is total revenues minus total costs: 

e.g.

We can write this profit in terms of either choice variable:

\pi(q) = pq - (wL^c(q) + r \overline K)
\pi(L) = pf(L) - (wL + r \overline K)

CONDITIONAL DEMAND FOR LABOR

Profit as a function of quantity

Profit as a function of labor

1. Costs and Revenues

2. Profit = total revenues minus total costs

3. Take derivative of profit function, set =0

\pi(q) = 12q - (64 + \tfrac{1}{4}q^2)
\pi^\prime(q) = 12 - {1 \over 2}q = 0
r(L) = p \times f(L) = 12 \sqrt{32L}

1. Costs and revenues

2. Profit = total revenues minus total costs

3. Take derivative of profit function, set =0

\pi(L) = 12\sqrt{32L} - (8L + 64)
\pi^\prime(L) = 12 \times \sqrt{8 \over L} - 8 = 0
q^* = 24
L^* = 18

Profit two ways when \(p = 12\), \(w = 8\), \(r = 2\), and \(\overline K = 32\)

c(q) = wL(q) + r\overline K = {1 \over 4}q^2 + 64
r(q) = pq = 12q
c(L) = wL + r\overline K = 8L + 64

PROFIT-MAXIMIZING OUTPUT CHOICE

PROFIT-MAXIMIZING INPUT CHOICE

MP_L = \tfrac{2}{3}

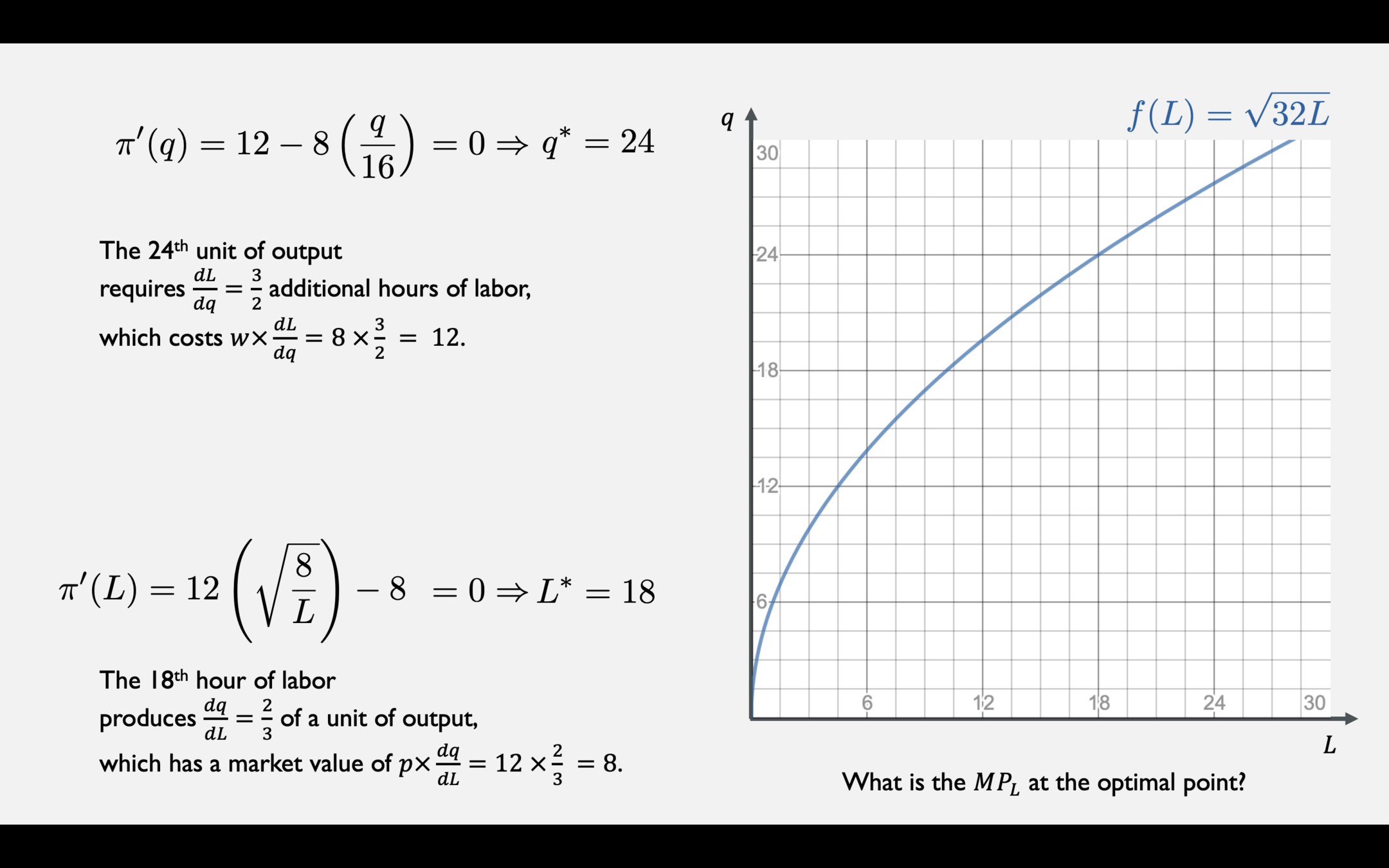
When price is fixed at 12

For a general price

1. Costs and Revenues

2. Profit = total revenues minus total costs

3. Take derivative of profit function, set =0

\pi(q) = 12q - (64 + \tfrac{1}{4}q^2)
\pi^\prime(q) = 12 - {1 \over 2}q = 0
r(q) = pq
\pi(q) = pq - (64 + \tfrac{1}{4}q^2)
\pi^\prime(q) = p - {1 \over 2}q = 0
q^* = 24
q^*(p) = 2p

Profit-Maximizing Output Choice when \(w = 8\), \(r = 2\), and \(\overline K = 32\)

c(q) = wL(q) + r\overline K = {1 \over 4}q^2 + 64
r(q) = pq = 12q
c(q) = wL(q) + r\overline K = {1 \over 4}q^2 + 64

NUMBER

FUNCTION

Labor Demand as a Function of \(w\) with Fixed \(p\)

When wage is fixed at 8

For a general wage

1. Costs and Revenues

2. Profit = total revenues minus total costs

3. Take derivative of profit function, set =0

Profit-Maximizing Labor Choice when \(p = 12\), \(r = 2\), and \(\overline K = 32\)

NUMBER

FUNCTION

r(L) = p \times f(L) = 12 \sqrt{32L}
\pi(L) = 12\sqrt{32L} - (wL + 64)
\pi^\prime(L) = 12 \times \sqrt{8 \over L} - w = 0
L^*(w) = {1152 \over w^2}
c(L) = wL + r\overline K = wL + 64
r(L) = p \times f(L) = 12 \sqrt{32L}
\pi(L) = 12\sqrt{32L} - (8L + 64)
\pi^\prime(L) = 12 \times \sqrt{8 \over L} - 8 = 0
L^* = 18
c(L) = wL + r\overline K = 8L + 64
f(L,K) = \sqrt{LK}, \overline K = 32
wL + 64
w
12\sqrt{32L}
\pi(L) = \ \ \ \ \ \ \ \ \ \ \ \ \ - [\ \ \ \ \ \ \ \ \ \ \ \ \ \ ]
\pi^\prime(q) = \ \ \ \ \ \ \ \ \ \ - \ \ \ \ = 0
12\sqrt{8 \over L}

TR

TC

MRPL

MC

Take derivative and set = 0:

Solve for \(L^*\):

L^*(w) = {1152 \over w^2}

PROFIT-MAXIMIZING
LABOR DEMAND FUNCTION

Output Supply and Labor Demand for General \(p\) and \(w\)

Profit as a function of output \(q\)

Profit as a function of labor \(L\)

c(q) = {wq^2 \over \overline K} + r \overline K

1. Costs for general \(w\) and revenue for general \(p\)

2. Profit = total revenues minus total costs

3. Take derivative of profit function, set =0

\pi(q) = pq - [{wq^2 \over 32} + 32r]
\pi^\prime(q) = p - {wq \over 16} = 0
r(L) = p\sqrt{32L}
\pi(L) = p\sqrt{32L} - [wL + 32r]
\pi^\prime(L) = p \times \sqrt{8 \over L} - w = 0
q^*(p\ |\ w) = {16 p \over w}
L^*(w\ |\ p) = {8p^2 \over w^2}
\text{Profit }\pi = pq - [wL + rK]
r(q) = p \times q
c(L) = wL + r \overline K

PROFIT-MAXIMIZING OUTPUT SUPPLY

PROFIT-MAXIMIZING LABOR DEMAND

f(L,K) = \sqrt{LK}, \overline K = 32
L^*(w\ |\ p) = 8 \left({p \over w}\right)^2

PROFIT-MAXIMIZING
LABOR DEMAND FUNCTION

q^*(p\ |\ w) = {16p \over w}

SUPPLY FUNCTION

the conditional labor demand
for the profit-maximizing supply:

L^*(w\ |\ p) = L^c(q^*(p\ |\ w))
L^c(q) = {1 \over 32} q^2
= {1 \over 32}\left(16p \over w\right)^2
= 8\left(p \over w\right)^2

The profit-maximizing labor demand is

CONDITIONAL LABOR DEMAND FUNCTION

Profit as a function of output \(q\)

Profit as a function of labor \(L\)

c(q) = wL(q) + r \overline K

1. Costs for general \(w\) and revenue for general \(p\)

2. Profit = total revenues minus total costs

3. Take derivative of profit function, set =0

\pi(q) = pq - [wL(q) + r\overline K]
\pi^\prime(q) = p - w \times {dL \over dq} = 0
r(L) = p \times f(L)
\pi(L) = p\times f(L) - [wL + r\overline K]
\pi^\prime(L) = p \times {dq \over dL} - w = 0
p = w \times {dL \over dq}
p \times {dq \over dL} = w
\text{Profit }\pi = pq - [wL + rK]
r(q) = p \times q
c(L) = wL + r \overline K

[cost of labor required for \(q\) units of output]

[revenue of output produced by \(L\) hours of labor]

MARGINAL COST (MC)

MARGINAL REVENUE PRODUCT OF LABOR (MRPL)

"Keep producing output as long as the marginal revenue from the last unit produced is at least as great as the marginal cost of producing it." 

"Keep hiring workers as long as the marginal revenue from the output of the last worker is at least as great as the cost of hiring them." 

p = MC
w = MRP_L

Profit as a function of output \(q\)

Profit as a function of labor \(L\)

p = w \times {1 \over MP_L}
w = p \times MP_L

What does this model tell us?

A competitive firm takes input prices \(w\) and \(r\), and the output price \(p\), as given.
We can therefore characterize its optimal choices of inputs and outputs
as functions of those prices: the supply of output \(q^*(p\ |\ w)\),
and the demand for inputs (e.g. \(L^*(w\ |\ p)\)).

We can find the optimal input-output combination either by finding the optimal quantity of output and determining the inputs required to produce it, or to find the profit-maximizing inputs and determine the resulting output. These two methods are equivalent.

Profit is increasing when marginal revenue is greater than marginal cost, and vice versa.
In most cases, the profit-maximizing choice occurs where \(MR = MC\).
If \(p\) is below the minimum value of AVC, the profit-maximizing choice is \(q = 0\).
In which MR or MC is discontinuous, logic must be applied. (There is an old exam question on the homework that explores this...and this kind of thing often shows up on exams...)

Is it true?

Are people paid the value of their marginal product?

What determines the value of people's work?

What should?

What determines how much people are paid?