pollev.com/chrismakler

What was Netscape Navigator?

How Markets “Choose" a
Point Along the PPF

Christopher Makler

Stanford University Department of Economics

Econ 50: Lecture 25

Unit IV: Equilibrium

Remaining lectures:
General Equilibrium

Analyze a single market, taking everything determined outside that market as given

(prices of other goods,
consumer income, wages)

Last two lectures:
Partial Equilibrium

Today: examine linkages between markets

Analyze all markets simultaneously

Wednesday: solve for equilibrium quantities in all markets simultaneously as a function only of production functions, resource constraints, and consumer preferences. 

(endogenize all prices, income, wages)

Today's Agenda

Labor Markets and the PPF

How Firms Collectively Maximize GDP

Short-Run Supply Response to a Shift in Demand

Review: the PPF and the MRT

Review: Competitive Firms' Demand for Labor

Long-Run Supply Responses and the Long Run Supply Curve

Multiple Uses of Resources

Labor

Fish

🐟

Coconuts

🥥

[GOOD 1]

⏳

[GOOD 2]

L_1
L_2
\overline L

Resource Constraint

L_1
L_2
L_1 + L_2 = \overline L
\overline L
\overline L
\text{Total labor available }=\overline L

Resource Constraints and the PPF

f_1(L_1) = 10\sqrt{L_1}
f_2(L_2) = 6\sqrt{L_2}
L_1 + L_2 = 100
0
10\sqrt{36}
60
100
0
6\sqrt{100}
60
48
6 \sqrt{64}
80
36

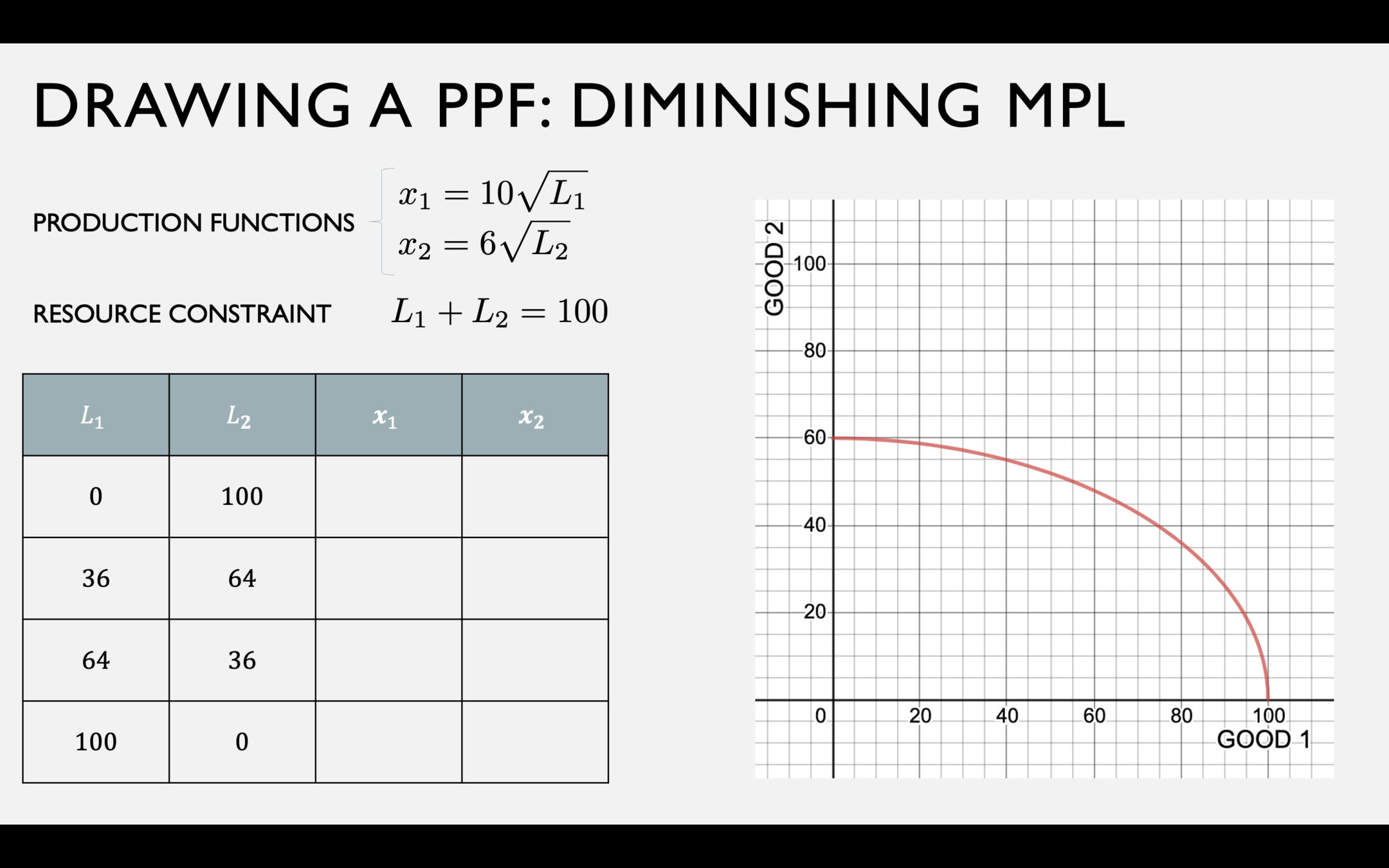
PPF

L_1 = {1 \over 100}x_1^2
L_2 = {1 \over 36}x_2^2
L_1
+
L_2
= 100
{1 \over 100}x_1^2
{1 \over 36}x_2^2
L_1 = {1 \over 100}x_1^2
L_2 = {1 \over 36}x_2^2
+
= 100
{1 \over 100}x_1^2
{1 \over 36}x_2^2

Slope of the PPF:
Marginal Rate of Transformation (MRT)

Rate at which one good may be “transformed" into another

...by reallocating resources from one to the other.

Opportunity cost of producing an additional unit of good 1,
in terms of good 2

Note: we will generally treat this as a positive number
(the magnitude of the slope)

This is just a level set of the function \(L(x_1,x_2) = {1 \over 3}x_1 + {1 \over 2}x_2\)

By the implicit function theorem:

\displaystyle{\text{slope of the level set}=-{{\partial L \over \partial x_1} \over {\partial L \over \partial x_2}}}
\displaystyle{=-{{1 \over 3} \over {1 \over 2}}}
\displaystyle{=-{2 \over 3}}
\displaystyle{\Rightarrow MRT ={2 \over 3}}

This is just a level set of the function \(L(x_1,x_2) = \)

By the implicit function theorem:

\displaystyle{\text{slope of the level set}=-{{dL_1 \over dx_1} \over {dL_2 \over dx_2}}}
\displaystyle{=-{{1 \over MP_{L1}} \over {1 \over {MP_{L2}}}}}
\displaystyle{=-{MP_{L2} \over MP_{L1}}}

Total labor required to produce the bundle \((x_1,x_2)\)

\(L_1(x_1) + L_2(x_2)\)

\({1 \over 3}x_1 + {1 \over 2}x_2\)

Recall: \(MP_{L1} = {dx_1 \over dL_1}, MP_{L2} = {dx_2 \over dL_2}\)

\displaystyle{\text{slope of the level set}=-{{\partial L \over \partial x_1} \over {\partial L \over \partial x_2}}}

Suppose we're allocating 100 units of labor to fish (good 1),
and 50 of labor to coconuts (good 2).

Now suppose we shift
one unit of labor
from coconuts to fish.

How many fish do we gain?

\Delta_2
\Delta_1

100

98

300

303

How many coconuts do we lose?

\Delta_2 = MP_{L_2} = 2\text{ coconuts}
\Delta_1 = MP_{L_1} = 3\text{ fish}
\left|\text{slope}\right| = \frac{MP_{L_2}}{MP_{L_1}}

Relationship between MPL's and MRT

x_1 = f_1(L_1) = 3L_1
x_2 = f_2(L_2) = 2L_2

Fish production function

Coconut production function

Resource Constraint

L_1 + L_2 = 150

PPF

This is a level set of the function \(L(x_1,x_2) = {1 \over 100}x_1^2 + {1 \over 36}x_2^2\)

By the implicit function theorem:

\displaystyle{\text{slope of the level set}=-{{\partial L \over \partial x_1} \over {\partial L \over \partial x_2}}}
\displaystyle{=-{{2 \over 100}x_1 \over {2 \over 36}x_2}}
\displaystyle{=-{9x_1 \over 25x_2}}
\displaystyle{\Rightarrow MRT ={9x_1 \over 25x_2}}

Profit as a function of quantity

Profit as a function of labor

1. Costs and Revenues

2. Profit = total revenues minus total costs

3. Take derivative of profit function, set =0

\pi(q) = 12q - (64 + \tfrac{1}{4}q^2)
\pi^\prime(q) = 12 - {1 \over 2}q = 0
r(L) = p \times f(L) = 12 \sqrt{32L}

1. Costs and revenues

2. Profit = total revenues minus total costs

3. Take derivative of profit function, set =0

\pi(L) = 12\sqrt{32L} - (8L + 64)
\pi^\prime(L) = 12 \times \sqrt{8 \over L} - 8 = 0
q^* = 24
L^* = 18

Profit two ways when \(p = 12\), \(w = 8\), \(r = 2\), and \(\overline K = 32\)

c(q) = wL(q) + r\overline K = {1 \over 4}q^2 + 64
r(q) = pq = 12q
c(L) = wL + r\overline K = 8L + 64

PROFIT-MAXIMIZING OUTPUT CHOICE

PROFIT-MAXIMIZING INPUT CHOICE

When wage is fixed at 8

For a general wage

1. Costs and Revenues

2. Profit = total revenues minus total costs

3. Take derivative of profit function, set =0

Profit-Maximizing Labor Choice when \(p = 12\), \(r = 2\), and \(\overline K = 32\)

NUMBER

FUNCTION

r(L) = p \times f(L) = 12 \sqrt{32L}
\pi(L) = 12\sqrt{32L} - (wL + 64)
\pi^\prime(L) = 12 \times \sqrt{8 \over L} - w = 0
L^*(w) = {1152 \over w^2}
c(L) = wL + r\overline K = wL + 64
r(L) = p \times f(L) = 12 \sqrt{32L}
\pi(L) = 12\sqrt{32L} - (8L + 64)
\pi^\prime(L) = 12 \times \sqrt{8 \over L} - 8 = 0
L^* = 18
c(L) = wL + r\overline K = 8L + 64
f(L,K) = \sqrt{LK}, \overline K = 32
wL + 64
w
12\sqrt{32L}
\pi(L) = \ \ \ \ \ \ \ \ \ \ \ \ \ - [\ \ \ \ \ \ \ \ \ \ \ \ \ \ ]
\pi^\prime(q) = \ \ \ \ \ \ \ \ \ \ - \ \ \ \ = 0
12\sqrt{8 \over L}

TR

TC

MRPL

MC

Take derivative and set = 0:

Solve for \(L^*\):

L^*(w) = {1152 \over w^2}

PROFIT-MAXIMIZING
LABOR DEMAND FUNCTION

Profit as a function of output \(q\)

Profit as a function of labor \(L\)

c(q) = {wq^2 \over \overline K} + r \overline K

1. Costs for general \(w\) and revenue for general \(p\)

2. Profit = total revenues minus total costs

3. Take derivative of profit function, set =0

\pi(q) = pq - [{wq^2 \over 32} + 32r]
\pi^\prime(q) = p - {wq \over 16} = 0
r(L) = p\sqrt{32L}
\pi(L) = p\sqrt{32L} - [wL + 32r]
\pi^\prime(L) = p \times \sqrt{8 \over L} - w = 0
q^*(p\ |\ w) = {16 p \over w}
L^*(w\ |\ p) = {8p^2 \over w^2}
\text{Profit }\pi = pq - [wL + rK]
r(q) = p \times q
c(L) = wL + r \overline K

PROFIT-MAXIMIZING OUTPUT SUPPLY

PROFIT-MAXIMIZING LABOR DEMAND

Profit as a function of output \(q\)

Profit as a function of labor \(L\)

c(q) = wL(q) + r \overline K

1. Costs for general \(w\) and revenue for general \(p\)

2. Profit = total revenues minus total costs

3. Take derivative of profit function, set =0

\pi(q) = pq - [wL(q) + r\overline K]
\pi^\prime(q) = p - w \times {dL \over dq} = 0
r(L) = p \times f(L)
\pi(L) = p\times f(L) - [wL + r\overline K]
\pi^\prime(L) = p \times {dq \over dL} - w = 0
p = w \times {dL \over dq}
p \times {dq \over dL} = w
\text{Profit }\pi = pq - [wL + rK]
r(q) = p \times q
c(L) = wL + r \overline K

[cost of labor required for \(q\) units of output]

[revenue of output produced by \(L\) hours of labor]

MARGINAL COST (MC)

MARGINAL REVENUE PRODUCT OF LABOR (MRPL)

"Keep producing output as long as the marginal revenue from the last unit produced is at least as great as the marginal cost of producing it." 

"Keep hiring workers as long as the marginal revenue from the output of the last worker is at least as great as the cost of hiring them." 

p = MC
w = MRP_L

Profit as a function of output \(q\)

Profit as a function of labor \(L\)

p = w \times {1 \over MP_L}
w = p \times MP_L

Labor Markets and the PPF

Notation

\(Y_1\) = total amount of good 1 produced by all firms in an economy

\(Y_2\) = total amount of good 2 produced by all firms in an economy

\(GDP(Y_1,Y_2) = p_1Y_1 + p_2Y_2\)
= market value of all final goods and services produced in an economy

Recall: market demand for a good is the horizontal sum of all individual demand curves:

The same is true for labor demand!

What happens to the individual and market labor demand when the price of good 1 goes up?

Let's do the math!

Suppose for simplicity that each good is produced by a single competitive firm.

Y_1 = 10\sqrt{L_1}
Y_2 = 6\sqrt{L_2}
MP_{L1} = {5 \over \sqrt{L_1}}
\text{Competitive firms set }w = p \times MP_L:
w = p_1 \times {5 \over \sqrt{L_1}}
L_1^*(w\ |\ p_1) = {25p_1^2 \over w^2}
MP_{L2} = {3 \over \sqrt{L_2}}
w = p_2 \times {3 \over \sqrt{L_2}}
L_2^*(w\ |\ p_2) = {9p_2^2 \over w^2}
L_1^*(w\ |\ p_1) = {25p_1^2 \over w^2}
L_2^*(w\ |\ p_2) = {9p_2^2 \over w^2}

Total labor demanded is the sum of the labor demanded by each firm, at any wage:

LD(w\ |\ p_1,p_2) = L_1^*(w\ |\ p_1) + L_2^*(w\ |\ p_2)
= {25p_1^2 \over w^2} + {9p_2^2 \over w^2}
= {25p_1^2 + 9p_2^2 \over w^2}
LD(w\ |\ p_1,p_2) =
= {25p_1^2 + 9p_2^2 \over w^2}

Suppose that labor is supplied inelastically at \(\overline L = 100\).

LS(w) = 100

We can solve for the equilibrium wage rate by equating labor demand and supply:

{25p_1^2 + 9p_2^2 \over w^2} = 100
w^* = {\sqrt{25p_1^2 + 9p_2^2} \over 10}

What happens to the individual and market labor demand when the price of good 1 goes up?

So, how does this affect output?

How Firms Collectively Maximize GDP

Resource Allocation

Narrow question: 
How many productive resources should we devote to a single good?

Broader question:
How should we allocate productive resources across goods?

Firms will choose the quantity at which \(p = MC\)

Firms will choose the point along the PPF at which \({p_1 \over p_2} = MRT\)

GDP maximizing point!!

How do firms
maximize GDP?

For a given set of prices \((p_1,p_2)\), what combination of outputs \((Y_1,Y_2)\) on our PDF would maximize GDP?

\(GDP(Y_1,Y_2) = p_1Y_1 + p_2Y_2\)

(Assume labor is the only input.)

pollev.com/chrismakler

What is the magnitude of the slope of an iso-GDP line?

The Social Planner's Problem

How do we maximize GDP subject to the PPF?

\text{s.t. }
\mathcal{L}(Y_1,Y_2,\lambda)=
\displaystyle{\max_{Y_1,Y_2}}
p_1Y_1 + p_2Y_2
\overline L - L_1(Y_1) - L_2(Y_2)
+ \lambda\ (
)

OBJECTIVE

FUNCTION

CONSTRAINT

p_1Y_1 + p_2Y_2
\overline L - L_1(Y_1) - L_2(Y_2) = 0
L_1(Y_1) + L_2(Y_2) = \overline L

DOLLARS

HOURS

What are the units?

DOLLARS

PER

HOUR

\mathcal{L}(Y_1,Y_2,\lambda)=
p_1Y_1 + p_2Y_2
\overline L - L_1(Y_1) - L_2(Y_2)
+ \lambda\ (
)
\displaystyle{\partial \mathcal{L} \over \partial Y_1} =

FIRST ORDER CONDITIONS

\displaystyle{\partial \mathcal{L} \over \partial Y_2} =
p_1
p_2
- \lambda\ \times
{dL_1 \over dY_1}
{dL_2 \over dY_2}
- \lambda\ \times
=0
=0
\displaystyle{\Rightarrow \lambda\ = \ \ \ \ \ \ \times}
\displaystyle{\Rightarrow \lambda\ = \ \ \ \ \ \ \times}
p_1
p_2
MP_{L1}
MP_{L2}

Tangency condition: 

{p_1 \over p_2} = {MP_{L2} \over MP_{L1}}

Firms setting their own MRPL equal to the wage rate will choose the point along the PPF at which \({p_1 \over p_2} = MRT\)

Conditions for
GDP Maximization

{p_1 \over p_2} = MRT

TANGENCY CONDITION

CONSTRAINT CONDITION

L_1(Y_1) + L_2(Y_2) = \overline L

Firms in industry 1 set \(w = p_1 \times MP_{L1}\)

Firms in industry 2 set \(w = p_2 \times MP_{L2}\)

How does competition achieve this?

Wages adjust until the
labor market clears

Effect of a Change in Demand

Consider two goods (“guns” and “butter”) which are unrelated
but which both use the same resource (e.g. labor) in production.

What happens in both markets 
if there is a demand shift
in the market for one of the goods?

pollev.com/chrismakler

Why did the wage rate go up in this model?

“Chain of Causality"

  • Increase in demand for good 1:
    • Movement up along the supply curve for good 1 → produce more good 1, increase \(p_1\)
    • Increase \(p_1\) → outward shift of the demand for labor from firms producing good 1
  • Increase in labor demand → equilibrium wage increases for all firms
  • Increase in wage affects supply of good 2:
    • Movement up along the labor demand curve for firms producing good 2
    • Inward shift of the supply curve for good 2 → produce less good 2
  • Secondary effect: increase in wage also reduces supply of good 1
  • Cumulative effect:
    • Produce more good 1 and less 2.
    • Use same amount of labor in total → stay along the PPF