Production and Cost
for a Firm

Christopher Makler

Stanford University Department of Economics

Econ 50 : Lecture 16

Today's Agenda

  • Overview of Unit III
  • Review of Econ 1 Treatment of Production and Cost
  • Total, Marginal, and Average Costs
  • Short-Run and Long-Run Costs
  • Curvature of Cost Functions

Unit I: The “Real Economy"

Labor

Fish

🐟

Capital

Coconuts

🥥

[GOODS]

⏳

⛏

[RESOURCES]

Utility

🤓

The story thus far...

Unit II: Consumers and Prices

Labor

Fish

🐟

Capital

Coconuts

🥥

[GOODS]

⏳

⛏

[RESOURCES]

🤓

p_1
p_2
m

Consumer

The story thus far...

Unit III: Theory of the Firm

Labor

Firm

🏭

Capital

⏳

⛏

Customers

🤓

p
w
r
q
L
K

This unit: analyze the firms
consumers buy things from

Unit III: Theory of the Firm

Firm

🏭

Costs

wL + rK

Customers

🤓

p
q

This unit: analyze the firms
consumers buy things from

Unit III: Theory of the Firm

Firm

🏭

Costs

wL + rK

Revenue

pq

From the firm's perspective, they get revenue and pay costs...

Unit III: Theory of the Firm

Costs

wL + rK

Revenue

pq

Profit

pq - (wL + rK)

...which is what we call profits

Unit III: Theory of the Firm

Costs

c(q) = wL(q) + r\overline K

Revenue

Profit

pq
pq - c(q)

Today: determine the firm's cost as a function of \(q\)

Wednesday: determine the firm's revenue as a function of \(q\)

Friday: find the firm's profit-maximizing value of \(q\)

r(q) = p(q) \times q
\pi(q) = r(q) - c(q)
wL + rK

Unit III: Theory of the Firm

How much output \(q\) does it supply as a function of the price of the good?

q^*(p)

How much labor \(L\) does it demand as a function of the wage rate?

L^\star(w)

Next week: analyze the behavior of a competitive (price-taking) firm

The Econ 1 Approach

Greg Mankiw, Principles of Economics

Greg Mankiw, Principles of Economics

Greg Mankiw, Principles of Economics

Greg Mankiw, Principles of Economics

Greg Mankiw, Principles of Economics

Dollars

Dollars Per Unit

The Econ 50 Approach

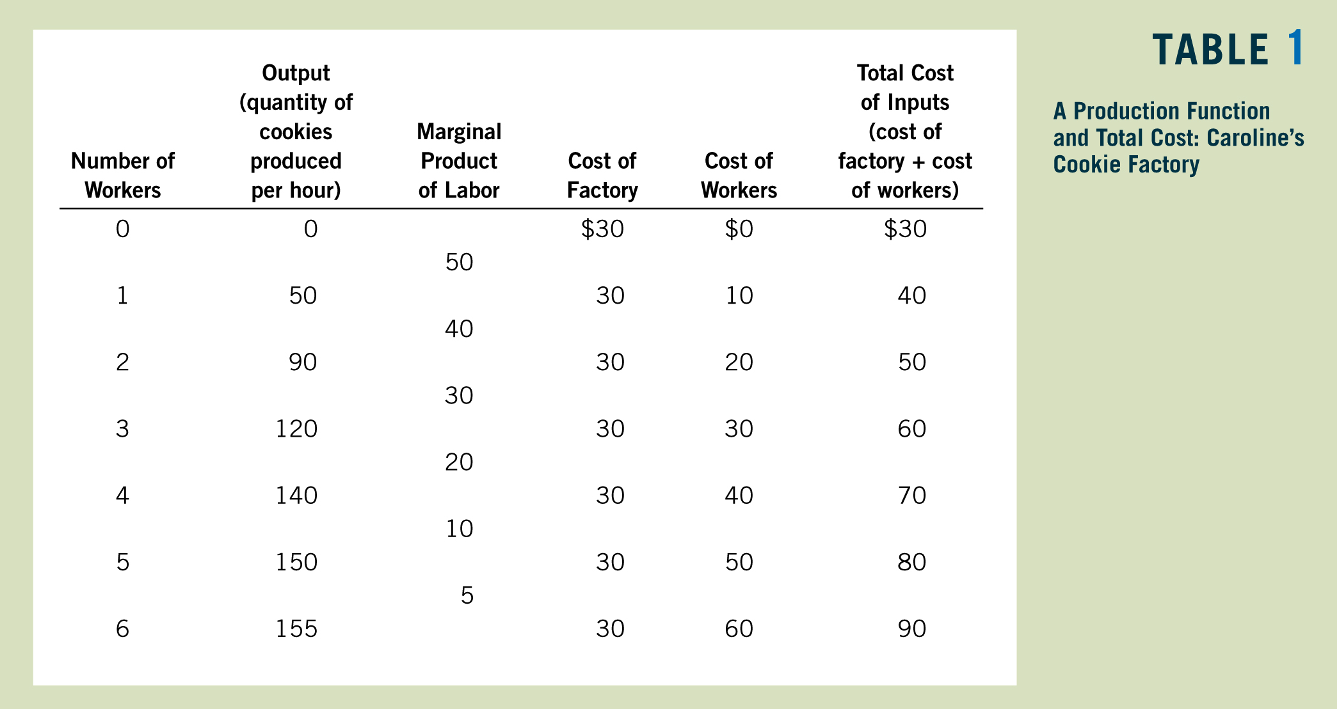
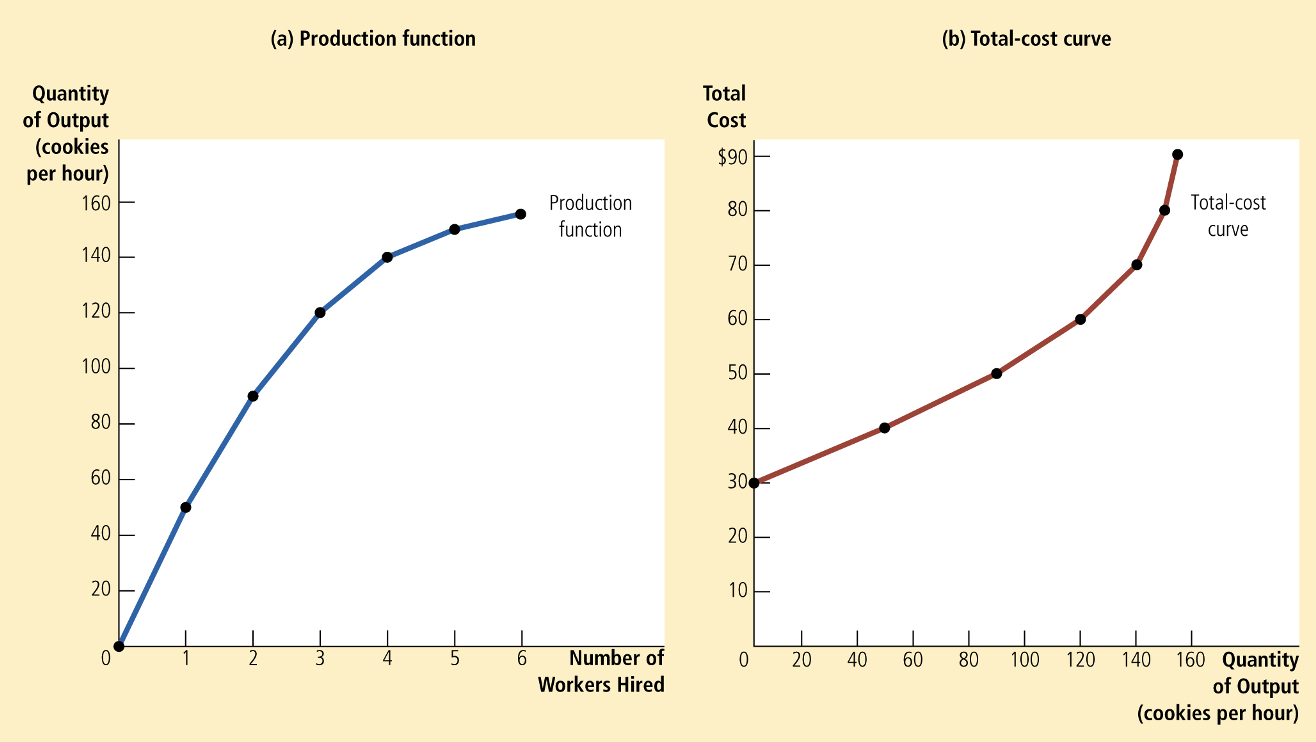
Let's start with just one input, labor, so \(q = f(L)\)

The total cost will be the cost of that labor input:

Just as with the PPF, we can talk about the labor required to produce \(q\) units of output, \(L(q)\)

\(TC(q) = wL(q)\)

\(TC(q) = wL(q)\)

Now, let's add capital.

We will assume that the level of capital is fixed in the short run at some amount \(\overline K\).

q = f(L\ |\ \overline K)

The amount of labor required to produce \(q\) units of output is therefore also going to depend upon \(\overline K\):

L(q\ |\ \overline K)

Short-Run Total Cost of \(q\) Units

TC(q\ |\ \overline{K}) = wL(q\ |\ \overline{K}) + r\overline{K}

Variable cost

"The total cost of producing \(q\) units in the short run is the variable cost of the required amount of the input that can be varied,
plus the fixed cost of the input that is fixed in the short run."

Fixed cost

f(L,K) = \sqrt{LK}

Short-run conditional demand for labor
if capital is fixed at \(\overline K\):

Total cost of producing \(q\) units of output:

L(q\ |\ \overline K) = {q^2 \over \overline K}
c(q\ |\ \overline{K}) = wL(q\ |\ \overline{K}) + r\overline{K} =
{wq^2 \over \overline K} + r\overline K

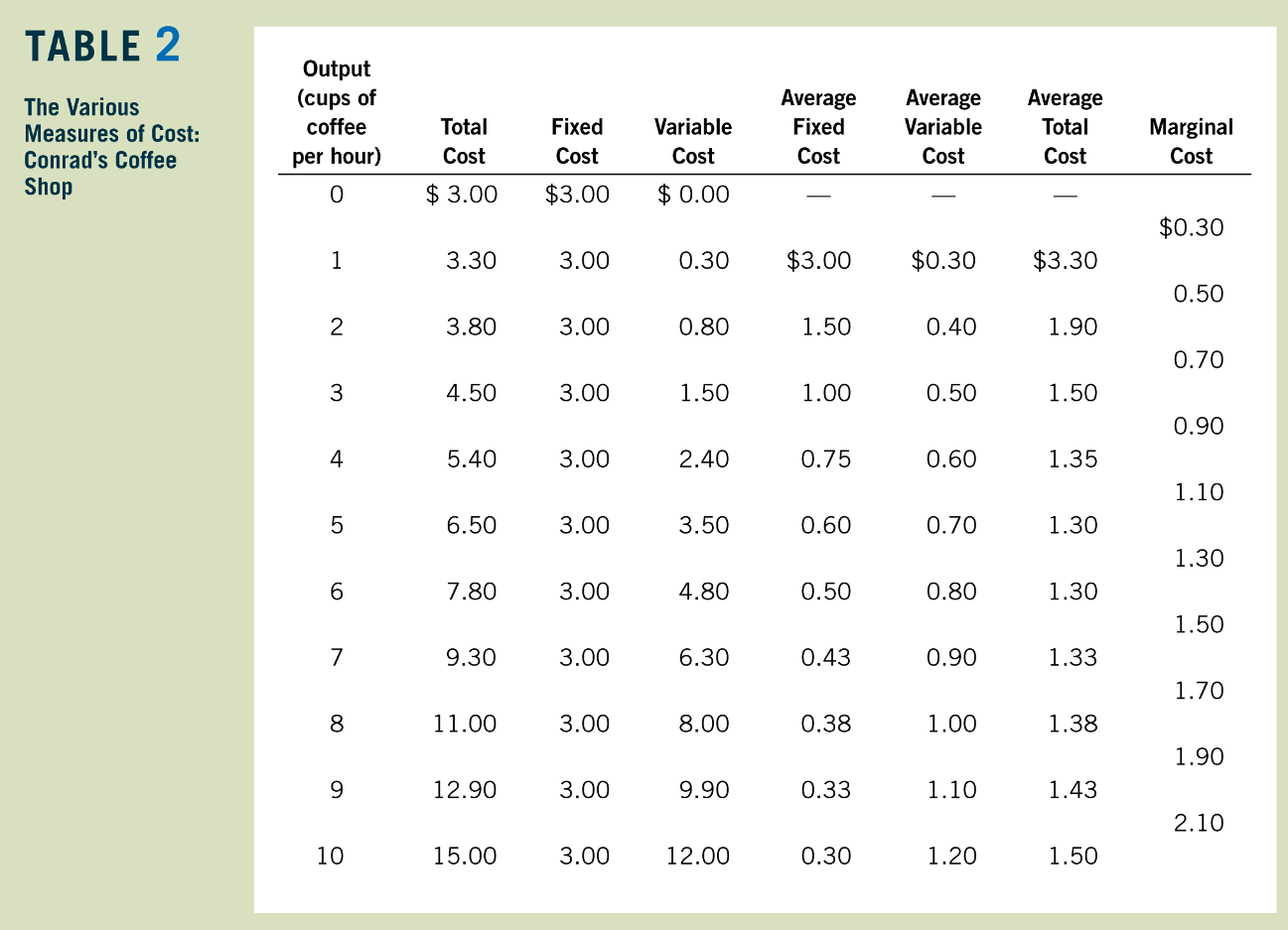
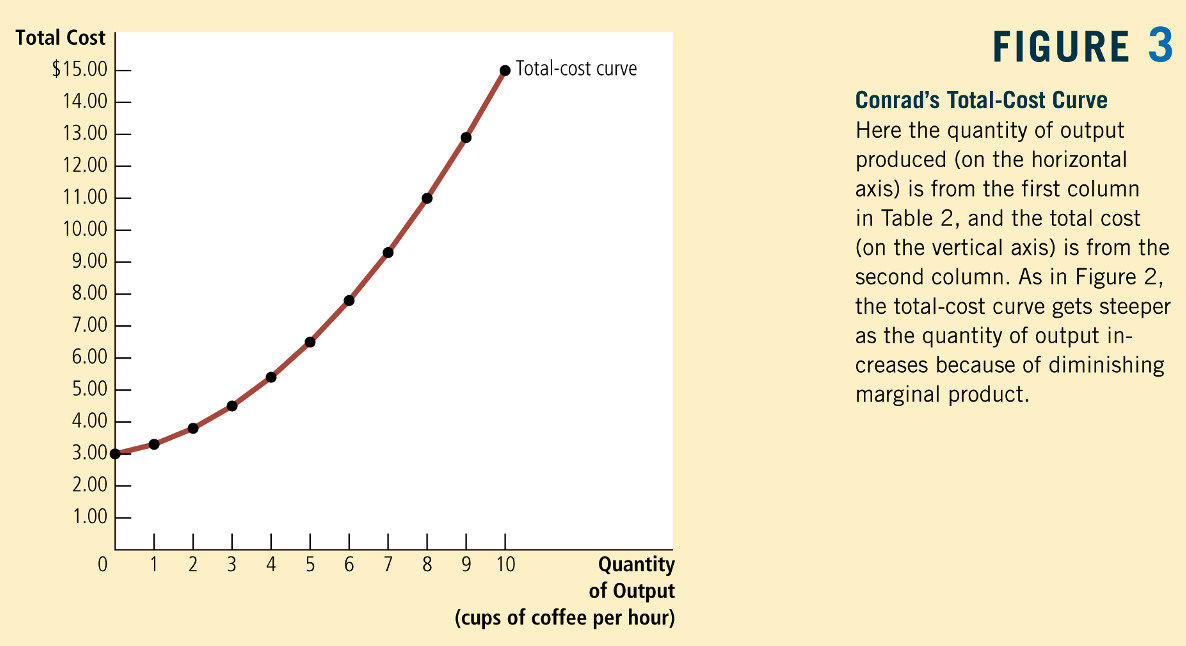
Total, Fixed and Variable Costs

c(q\ |\ \overline{K}) =

Fixed Costs \((F)\): All economic costs
that don't vary with output.

Variable Costs \((VC(q))\): All economic costs
that vary with output

explicit costs (\(r \overline K\)) plus
implicit costs like opportunity costs

r\overline{K}
wL(q,\overline{K})
+
TC(q) =
+
F
VC(q)

e.g. cost of labor required to produce
\(q\) units of output given \(\overline K\) units of capital

TC(q) = {wq^2 \over \overline K} + r\overline K
VC(q) = {wq^2 \over \overline K}
F = r\overline K

pollev.com/chrismakler

Generally speaking, if capital is fixed in the short run, then higher levels of capital are associated with _______ fixed costs and _______ variable costs for any particular target output.

\text{Total Cost}: TC(q) = F + VC(q)
\text{Average Cost}: ATC(q) = \frac{TC(q)}{q} = \frac{F}{q} + \frac{VC(q)}{q}

Fixed Costs

Variable Costs

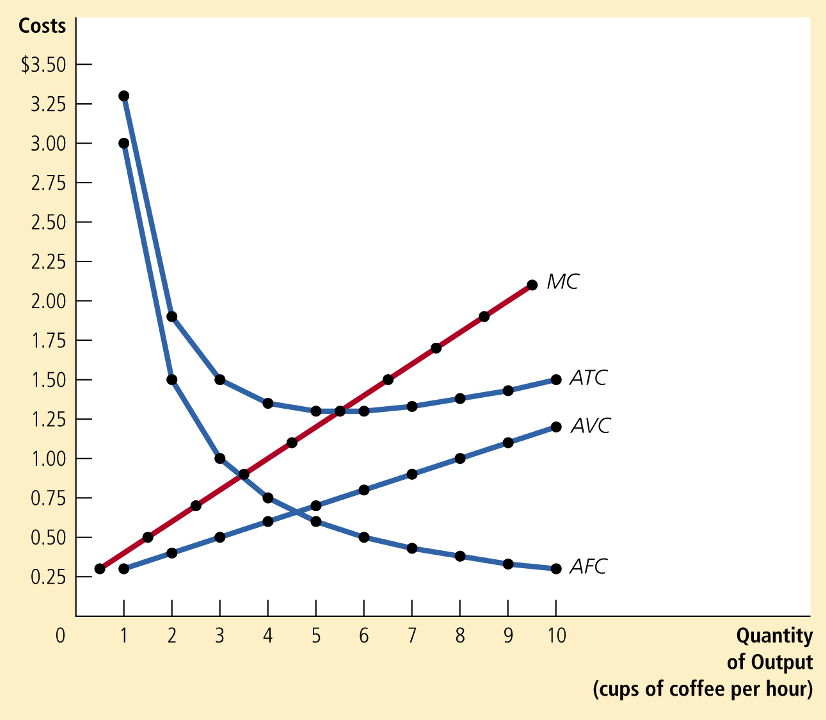
Average Fixed Costs (AFC)

Average Variable Costs (AVC)

Average Costs

\text{Total Cost}: TC(q) = F + VC(q)
\text{Average Cost}: ATC(q) = \frac{F}{q} + \frac{VC(q)}{q}

Average Costs

TC(q) = 64 + {1 \over 4}q^2
ATC(q) = {64 \over q} + {1 \over 4}q
\text{Total Cost}: TC(q) = F + VC(q)
\text{Marginal Cost}: MC(q) = TC'(q) = 0 + VC'(q)

Fixed Costs

Variable Costs

Marginal Cost

(marginal cost is the marginal variable cost)

\text{Total Cost}: TC(q) = F + VC(q)
\text{Marginal Cost}: MC(q) = TC'(q)

Marginal Cost

TC(q) = 64 + {1 \over 4}q^2
MC(q) = {1 \over 2}q

pollev.com/chrismakler

Suppose q* is the quantity
for which ATC is lowest.

Which of the following must be true?

(Assume that ATC and MC are continuous functions of q.)

(a) MC also reaches its minimum at q*

(b) MC reaches its maximum at q*

(c) MC and ATC are equal at q*

Marginal cost tends to "pull" average cost toward it:

MC > AC \Rightarrow AC \text{ increasing}
MC = AC \Rightarrow AC \text{ constant}
MC < AC \Rightarrow AC \text{ decreasing}

Marginal grade = grade on last test, average grade = GPA

Relationship between Average and Marginal Costs

Relationship between Marginal Cost and Marginal Product of Labor

TC(q) = wL^c(q | \overline K) + r \overline K
{dTC(q) \over dq} = w \times {dL^c(q) \over dq}
= w \times {1 \over MP_L}

Next Time

  • Think about the demand curve facing a firm
  • Analyze the price elasticity of demand
  • Analyze the total and marginal revenue from producing more output
  • Friday: bring cost and revenue together

Cost Minimization

Cost Minimization Subject to a Utility Constraint

Cost Minimization Subject to an Output Constraint

\min p_1x_1 + p_2x_2 \text{ s.t. } u(x_1,x_2) = U
\min wL + rK \text{ s.t. } f(L,K) = q
\text{solutions}: x_1^c(p_1,p_2,U), x_2^c(p_1,p_2,U)
\text{solutions}: L^c(w,r,q), K^c(w,r,q)

Hicksian Demand

Conditional Demand

Cost Minimization: Lagrange Method

\mathcal{L}(L,K,\lambda)=
wL + rK +
(q - f(L,K))
\lambda
\frac{\partial \mathcal{L}}{\partial x_1} = w - \lambda MP_L

First Order Conditions

\frac{\partial \mathcal{L}}{\partial x_2} = r - \lambda MP_K
\frac{\partial \mathcal{L}}{\partial \lambda} = q - f(L,K) = 0 \Rightarrow q = f(L,K)
= 0 \Rightarrow \lambda = w \times {1 \over MP_L}
= 0 \Rightarrow \lambda = r \times \frac{1}{MP_K}

MRTS (slope of isoquant) is equal to the price ratio

\text{Also: }\frac{\partial \mathcal{L}}{\partial q} = \lambda = \text{Marginal cost of producing last unit using either input}
\text{Set two expressions }
\text{for }\lambda \text{ equal:}
\frac{MP_L}{MP_K} = \frac{w}{r}
f(L,K) = \sqrt{LK}

Tangency condition: \(MRTS = w/r\)

Constraint: \(q = f(L,K)\)

MRTS = {MP_L \over MP_K} =
{{1 \over 2}L^{-{1 \over 2}}K^{1 \over 2} \over {1 \over 2}L^{1 \over 2}K^{-{1 \over 2}}}
= {K \over L}

Conditional demands for labor and capital:

Total cost of producing \(q\) units of output:

Expansion Path

A graph connecting the input combinations a firm would use as it expands production: i.e., the solution to the cost minimization problem for various levels of output

Exactly the same as the income offer curve (IOC) in consumer theory.

(And, if the optimum is found via a tangency condition, exactly the same as the tangency condition.)

Long-Run Total Cost of \(q\) Units

c^{LR}(q) = wL^c(w,r,q) + rK^c(w,r,q)

Conditional demand for labor

Conditional demand for capital

"The total cost of producing \(q\) units in the long run
is the cost of the cost-minimizing combination of inputs
that can produce \(q\) units of output."

Exactly the same as the expenditure function in consumer theory.

f(L,K) = \sqrt{LK}

 Long Run (can vary both labor and capital)

L^c(q) = \sqrt{\frac{r}{w}}q
K^c(q) = \sqrt{\frac{w}{r}}q
TC^{LR}(q) = wL^c(q) + rK^c(q)
=2\sqrt{wr}q

 Short Run with Capital Fixed at \(\overline K \)

L^c(q | \overline K) = {q^2 \over \overline K}
TC(q) = wL^c(q | \overline K) + r \overline K
={wq^2 \over \overline K} + r \overline K
f(L,K) = \sqrt{LK}

 Long Run (can vary both labor and capital)

TC^{LR}(q)=2\sqrt{wr}q

 Short Run with Capital Fixed at \(\overline K \)

TC(q)={wq^2 \over \overline K} + r \overline K

Let's fix \(w= 8\), \(r = 2\), and \(\overline K =32\)

TC^{LR}(q)=8q
TC(q)=64 + {1 \over 4}q^2
TC(q)=64 + {1 \over 4}q^2
F = 64
VC(q) = {1 \over 4}q^2

Relationship between
Short-Run and Long-Run Costs

TC(q | \overline{K}) = \text{Cost if capital is fixed at }\overline{K}
TC(q,K^c(q)) = \text{Cost if capital is fixed at optimal }K \text{ for producing }q

What conclusions can we draw from this?

TC(q,\overline{K}) \ge TC^{LR}(q)
= TC^{LR}(q)
TC^{LR}(q) \text{ is the lower envelope of the family of }TC(q)\text{ curves}

Returns to a Single Input

  • Increasing marginal product: MPL is increasing in L
  • Constant marginal product: MPL is constant in L
  • Diminishing marginal product: MPL is decreasing in L

Returns to Scale (Scaling all inputs.)

  • Increasing returns to scale: doubling all inputs more than doubles output.
  • Constant returns to scale: doubling all inputs exactly doubles output.
  • Decreasing returns to scale: doubling all inputs less than doubles output.

Relationship between Production Function and the Curvature of Long-Run and Short-Run Costs

  • If the production function has diminishing \(MP_L\), the short-run cost curve will get steeper as you produce more output
  • If the production function has decreasing returns to scale, the long-run cost curve will get steeper as you produce more output.
  • What about for constant returns to scale? Increasing returns to scale? 
  • Homework question 15.1 walks you through these...

Economies and Diseconomies of Scale

Returns to Scale

Has to do with the production function

Economies of Scale

Has to do with cost curves

Increasing Returns to Scale:
double input => more than double output

Decreasing Returns to Scale:
double input => less than double output

Always deals with the long run

Can occur in both the long run and short run

Economies of Scale:
increasing output lowers average costs

Diseconomies of Scale:
increasing output raises average costs