Intertemporal Choice
Christopher Makler
Stanford University Department of Economics
Econ 51: Lecture 3
Today's Agenda
Part 1: Baseline Case
Part 2: Extensions and Applications
Modeling present-future tradeoffs
The intertemporal budget constraint
Preferences over time
Optimal saving and borrowing
Different interest rates for borrowing and saving
Credit constraints
Real and nominal interest rates
Beyond two time periods
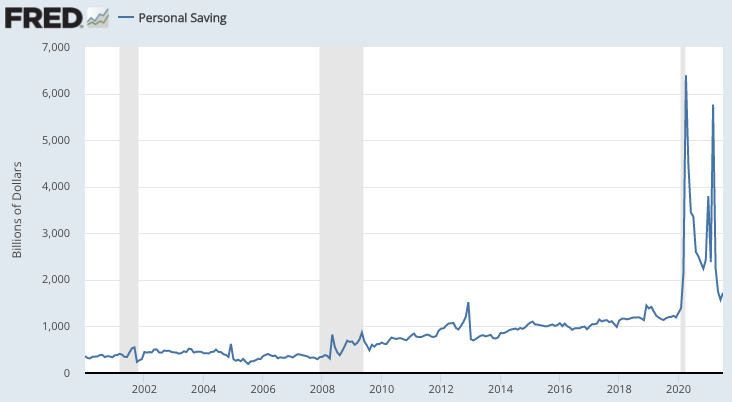
Saving and borrowing is a huge part of the U.S. economy.

Endowment of time and money.
Today: Present vs. Future Consumption
Endowment of money in different time periods (an "income stream")
Last time: Leisure vs. Consumption
Working = trading time for money
Saving = trading present consumption for future consumption
Borrowing = trading future consumption for present consumption
For Each Context:
Determine the budget line
Analyze preferences
Solve for optimal choice
Comparative statics: analyze net supply and demand
Do you have to spend all the money you earn in the period when you earn it?
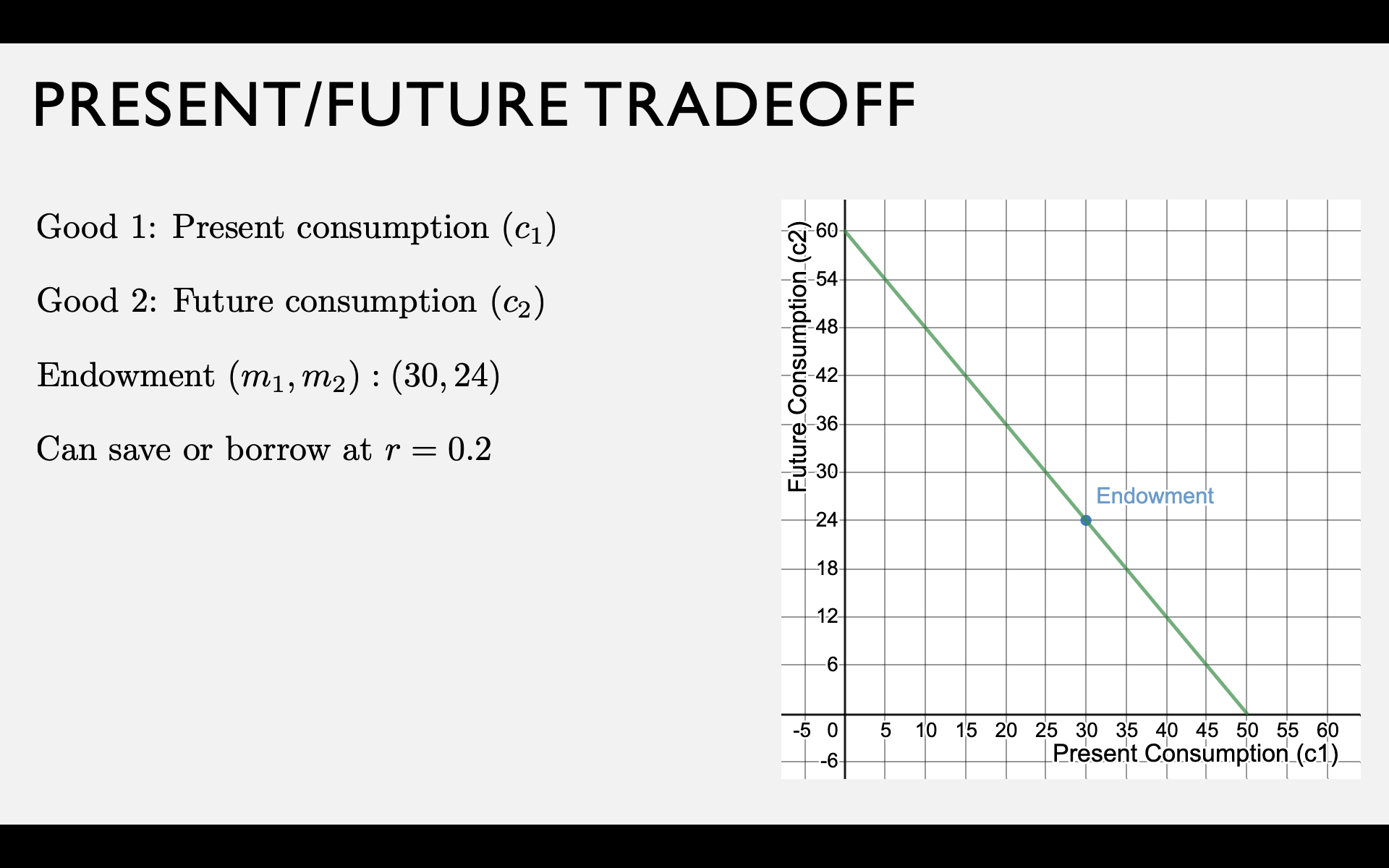
Present-Future Tradeoff
Your endowment is an income stream of \(m_1\) dollars now and \(m_2\) dollars in the future.
What happens if you don't consume all \(m_1\) of your present income?
Two "goods" are present consumption \(c_1\) and future consumption \(c_2\).
Let \(s = m_1 - c_1\) be the amount you save.
Saving and Borrowing with Interest
If you save at interest rate \(r\),
for each dollar you save today,
you get \(1 + r\) dollars in the future.
You can either save some of your current income, or borrow against your future income.
If you borrow at interest rate \(r\),
for each dollar you borrow today,
you have to repay \(1 + r\) dollars in the future.
"Future Value"

"Present Value"

Preferences over Time
Examples:
When to borrow and save?
Save if MRS at endowment < \(1 + r\)
Borrow if MRS at endowment > \(1 + r\)
(high interest rates or low MRS)
(low interest rates or high MRS)
If we assume \(v(c)\) exhibits diminishing marginal utility:
MRS is higher if you have less money today (\(m_1\) is low)
and/or more money tomorrow (\(m_2\) is high)
MRS is lower if you are more patient (\(\beta\) is high)
Save if MRS at endowment < \(1 + r\)
Borrow if MRS at endowment > \(1 + r\)
pollev.com/chrismakler

If \(m_1 = 30\), \(m_2 = 24\), and \(\beta = 0.5\),
what is the highest interest rate at which you would borrow money?
Borrow or Save?
Optimal Bundle
Tangency condition:
Budget line:
If \(m_1 = 30\), \(m_2 = 24\), \(\beta = 0.25\), and \(r = 0.2\),
what is your optimal choice?
pollev.com/chrismakler

Optimal Bundle
Tangency condition:
Budget line:
Since you start with \(m_1 = 30\), this means you borrow 10.
Supply of Savings and
Demand for Borrowing
In general, net demand is \(x_1^* - e_1\)
In this context, net demand is the demand for borrowing.
If it's negative, then it's the supply of saving.
Different Interest Rates
BORROW
SAVE
What if the interest rate is different for borrowing and saving?

When a Budget Line Ends...
Inflation and Real Interest Rates
Suppose there is inflation,
so that each dollar saved can only buy
\(1/(1 + \pi)\) of what it originally could:
Up to now, we've been just looking at
dollar amounts in both periods
We call \(r\) the "nominal interest rate" and \(\rho\) the "real interest rate"
For low values of \(r\) and \(\pi\), \(\rho \approx r - \pi\)
"Present Value" for two periods
Beyond Two Periods
If you save \(s\) now, you get \(x = s(1 + r)\) next period.
The amount you have to save in order to get \(x\) one period in the future is
Remember how we got this...
If you save \(s\) now, you get \(x = s(1 + r)\) next period.
The amount you have to save in order to get \(x\) one period in the future is
If you save for two periods, it grows at interest rate \(r\) again, so \(x_2 = (1+r)(1+r)s = (1+r)^2s\)
Therefore, the amount you have to save in order to get \(x_2\) two periods in the future is
If you save for two periods, it grows at interest rate \(r\) again, so \(x_2 = (1+r)(1+r)s = (1+r)^2s\)
Therefore, the amount you have to save in order to get \(x_2\) two periods in the future is
If you save for \(t\) periods, it grows at interest rate \(r\) each period, so \(x_t = (1+r)^ts\)
Therefore, the amount you have to save in order to get \(x_t\), \(t\) periods in the future, is
Therefore, the amount you have to save in order to get \(x_t\), \(t\) periods in the future, is
We call this the present value of a payoff of \(x_t\)
Application: Social Cost of Carbon
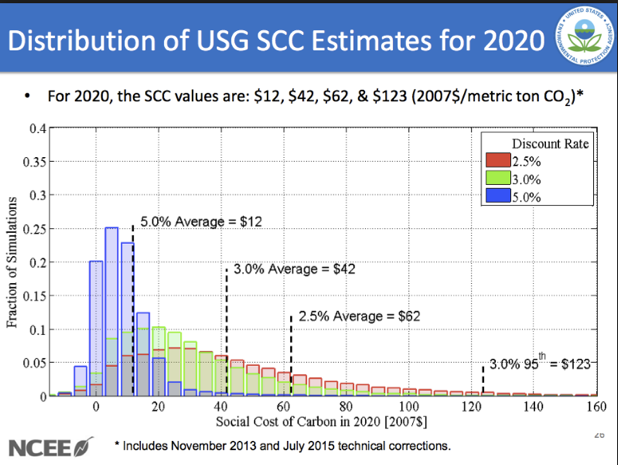
Obama Admin: $45
Uses a 3% discount rate; includes global costs
Trump Admin: less than $6
Uses a 7% discount rate; only includes American costs
PV of $1 Trillion in 2100:
$86B for Obama, $4B for Trump