Job Market Signaling & The Market for Lemons
Christopher Makler
Stanford University Department of Economics
Econ 51: Lecture 15
Perfect Bayesian Equilibrium
Consider a strategy profile for the players, as well as beliefs over the nodes at all information sets.
These are called a perfect Bayesian Equilibrium (PBE) if:
- Each player’s strategy is optimal to them at each infoset, given beliefs at this infoset and opponents’ strategies (“Sequential Rationality”)
- The beliefs are obtained from strategies using Bayes’ Rule wherever possible (i.e. at each infoset that is reached with a positive probability) (“consistency of beliefs”)
Separating and Pooling Equilibria
Separating Equilibrium: Each type of informed player chooses differently,
thereby conveying information about their type to the uninformed player
Pooling Equilibrium: Each type of informed player chooses the same,
thereby leaving the uninformed player with their prior belief.
Steps for calculating perfect Bayesian equilibria: Guess and Check!
- Start with a strategy for player 1 (pooling or separating).
- If possible, calculate updated beliefs (q in the example) by using Bayes’ rule.
In the event that Bayes’ rule cannot be used, you must arbitrarily select an updated belief; here you will generally have to check different potential values for the updated belief with the next steps of the procedure. - Given the updated beliefs, calculate player 2’s optimal action.
- Check whether player 1’s strategy is a best response to player 2’s strategy.
If so, you have found a PBE.
There are two types of workers: "high-ability" and "low-ability."
High-ability workers
are worth \(y_H\) to a firm
Low-ability workers
are worth \(y_L\) to a firm
Assume both firms and high-ability workers would be better off if firms could observe their ability.
Need some mechanism to create a separating equilibrium.

Job Market Signaling
Job Market Signaling
Nature determines each worker's type; \({1 \over 3}\) are H, \({2 \over 3}\) are L.
NATURE
Type-H Worker
Type-L Worker
The worker realizes their own type,
and chooses whether to go to college
or stick with a high school degree.
Firms choose to put each worker into a Management or Clerical job.
Management jobs pay 10; clerical jobs pay 4.
High school is free, so workers get that salary.
College reduces pay, but not equally: it costs type-H workers 4, but type-L workers 7.
A type-H worker in a Management position is worth 10 to a firm.
A type-L worker in a Management position is worth 0 to a firm.
Anyone in a Clerical position is worth 4 to a firm.
Job Market Signaling
Nature determines each worker's type; \({1 \over 3}\) are H, \({2 \over 3}\) are L.
NATURE
Type-H Worker
Type-L Worker
The worker realizes their own type,
and chooses whether to go to college
or stick with a high school degree.
Firms cannot observe the worker's type;
they can only observe whether
they chose High School or College.
The firm has beliefs about the worker's type based on that choice:
Job Market Signaling
NATURE
Type-H Worker
Type-L Worker
Consider a separating equilibrium in which type-H workers choose College, and type-L workers choose High School:
What are the firm's beliefs?

Job Market Signaling
NATURE
Type-H Worker
Type-L Worker
Consider a separating equilibrium in which type-H workers choose College, and type-L workers choose High School:
What are the firm's beliefs?
Reason: if all type-H's choose College,
and all type-L's choose High School,
then observing the worker's choice conveys all relevant information to the firm.
Job Market Signaling
NATURE
Type-H Worker
Type-L Worker
Consider a separating equilibrium in which type-H workers choose College, and type-L workers choose High School:
What are the firm's beliefs?
What is the firm's best response to workers' strategies and this set of beliefs?

Job Market Signaling
NATURE
Type-H Worker
Type-L Worker
Candidate separating equilibrium:
Important! A PBE must specify
both strategies and beliefs.
Also...we're not done!!!
We need to check that workers don't want to deviate given the strategies of firms.
Job Market Signaling
NATURE
Type-H Worker
Type-L Worker
Given that firms place
college grads in management positions,
and high school grads in clerical jobs:
Is it worth it for type-H workers to go to college?
Would it be worth it for type-L workers to go to college?
YES
NO
Job Market Signaling
NATURE
Type-H Worker
Type-L Worker
Could there be a pooling equilibrium in which everyone goes to college?
What is the firm's best response for this \(q\)?

If both types go to college, what is \(q\)?
Job Market Signaling
NATURE
Type-H Worker
Type-L Worker
Could there be a pooling equilibrium in which no one goes to college?
The Market For Lemons
(Akerlof 1970)
There are two types of used cars: "lemons" and "plums"
- Lemons (🍋) are worth $1000 to a seller and $1200 to a buyer
- Plums (🥭) are worth $2000 to a seller and $2400 to a buyer
If the quality of a car is observable to a buyer, which types of cars will sell?
If the quality is not observable to a buyer, and an equal number of each type of cars are on the market, what is the expected value to a buyer from buying a random car?
If that's the most buyers are willing to spend, which cars will be offered for sale?
🍋
🥭

$1800
🍋
There are two types of used cars: "lemons" and "plums"
- Lemons (🍋) are worth $1000 to a seller and $1200 to a buyer
- Plums (🥭) are worth $2000 to a seller and $2400 to a buyer
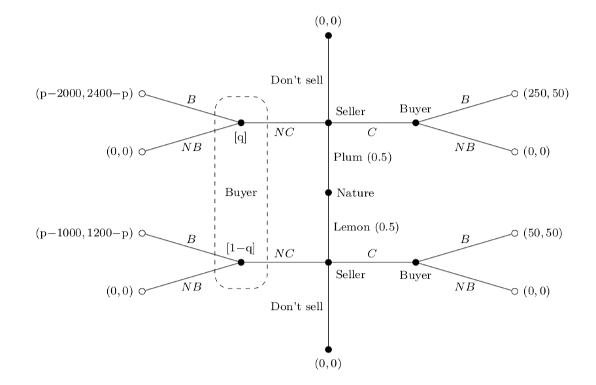
Suppose the seller could pay $100 to get their car quality certified (C).
Assume that if the car is certified, its quality is revealed and it is sold for $50 less than the buyer value.
If a car is not certified, its quality is still unknown.
🍋
🥭
(The seller can also choose not to sell)
There are two types of used cars: "lemons" and "plums"
- Lemons (🍋) are worth $1000 to a seller and $1200 to a buyer
- Plums (🥭) are worth $2000 to a seller and $2400 to a buyer

🍋
🥭
Separating PBE:
Sellers of plus get their cars certified.
Sellers of lemons do not.
Buyers of uncertified cars believe an uncertified car
is a lemon (q = 0)
and pay p = 1150.
(150, 50)
(-850, 1250)