Dynamic Games of Incomplete Information
Christopher Makler
Stanford University Department of Economics
Econ 51: Lecture 14
Poker Night: Next Thursday
- I'm in. So is Scott.
- Econ 50, 51, 102A
- Details TBA...stay tuned
- Beliefs and Updating
- Perfect Bayesian Equilibrium
- Job Market Signaling
Today's Agenda
- Complete information: everyone knows everything about the game
- Incomplete information: players have private information
(e.g., they know what their valuation of a good is)
- Incomplete information: players have private information
- Perfect information: everyone can perfectly observe everyone else's moves
- Imperfect information: players' moves are hidden from other players
(e.g. I cannot observe how much time you spend studying)
- Imperfect information: players' moves are hidden from other players
Information
Time
Information
Static
(Simultaneous)
Dynamic
(Sequential)
Complete
Incomplete
WEEK 5
WEEK 6
LAST TIME
TODAY
Prisoners' Dilemma
Cournot
Entry Deterrence
Stackelberg
Auctions
Job Market Signaling
Collusion
Cournot with Private Information
Poker
Time
Information
Static
(Simultaneous)
Dynamic
(Sequential)
Complete
Incomplete
Strategy: an action
Equilbirium: Nash Equilibrium
Strategy: a mapping from the history of the game onto an action.
Equilibrium: Subgame Perfect NE
Strategy: a plan of action that
specifies what to do after every possible history of the game, based on one's own private information and (updating) beliefs about other players' private information.
Equilibrium: Perfect Bayesian Equilibrium
Strategy: a mapping from one's private information onto an action.
Equilibrium: Bayesian NE
WEEK 5
WEEK 6
LAST TIME
TODAY
Prisoners' Dilemma
Cournot
Entry Deterrence
Stackelberg
Auctions
Job Market Signaling
Collusion
Cournot with Private Information
Poker
Example: Gift-Giving
She chooses to give one of three gifts:
X, Y, or Z.
1
X
Y
Z
Player 1 makes the first move.
Example: Gift-Giving
Twist: Gift X is unwrapped,
but Gifts Y and Z are wrapped.
(Player 1 knows what they are,
but player 2 does not.)
After each of player 1's moves,
player 2 has the move: she can either accept the gift or reject it.
2
Accept X
Reject X
2
1
X
Y
Z
We represent this by having an information set connecting
player 2's decision nodes
after player 1 chooses Y or Z.
2
2
Accept Y
Reject Y
Accept Z
Reject Z
Also: player 2 cannot make her action contingent on Y or Z; her actions must be "accept wrapped" or "reject wrapped"
Accept Wrapped
Reject Wrapped
Accept Wrapped
Reject Wrapped
Example: Gift-Giving
After player 2 accepts or rejects the gift, the game ends (terminal nodes) and payoffs are realized.
1
0
1
0
2
0
2
0
3
0
–1
0
2
2
1
X
Y
Z
,
,
,
,
,
,
Accept X
Reject X
Accept Wrapped
Reject Wrapped
Accept Wrapped
Reject Wrapped
In this game, both players get a payoff of
0 if any gift is rejected,
1 if gift X is accepted, and
2 if gift Y is accepted.
If gift Z is accepted, player 1 gets a payoff of 3, but player 2 gets a payoff of –1.
1
0
1
0
2
0
2
0
3
0
–1
0
2
2
1
X
Y
Z
,
,
,
,
,
,
Accept X
Reject X
Accept Wrapped
Reject Wrapped
Accept Wrapped
Reject Wrapped
Intuitively, what should the equilibrium of this game be? Why?
Player 2:
Player 1:
Accept X
Reject a Wrapped Gift
X
Player 2:
Player 1:
Accept everything
Z
This is a subgame. From this subgame,
we know player 2 will accept X if given X.
What about player 2's other strategy?
Why isn't this an equilibrium?
1
0
1
0
2
0
2
0
3
0
–1
0
2
2
1
X
Y
Z
,
,
,
,
,
,
Accept X
Reject X
Accept Wrapped
Reject Wrapped
Accept Wrapped
Reject Wrapped
We need some new concept to make player 2 reject a wrapped gift, if offered one.
Solution: we'll say that player 2 has to have beliefs about which gift was given, if it is wrapped.
1
0
1
0
2
0
2
0
3
0
–1
0
2
2
1
X
Y
Z
,
,
,
,
,
,
Accept X
Reject X
Accept Wrapped
Reject Wrapped
Accept Wrapped
Reject Wrapped
Solution: we'll say that player 2 has to have beliefs about which gift was given, if it is wrapped.
Player 2:
Player 1:
Accept X
Reject a Wrapped Gift
X
STRATEGIES
BELIEFS
Player 2:
\(p < {1 \over 3}\)
(Player 2 believes that if they're given a wrapped gift, it's probably Z.
Bayes' Rule and Conditional Beliefs
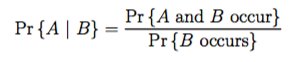

Suppose you don't know whether it's raining out,
but you can observe whether
I'm carrying an umbrella or not.
Ex ante, you believe the joint probabilities
of these events are given by this table:
Bayes' Rule:
Before you see whether I'm carrying an umbrella, with what probability do you believe it's raining?

Bayes' Rule and Conditional Beliefs
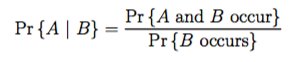

Suppose you don't know whether it's raining out,
but you can observe whether
I'm carrying an umbrella or not.
Ex ante, you believe the joint probabilities
of these events are given by this table:
Bayes' Rule:

Suppose you see me with an umbrella. Now with what probability do you think it's raining?
Conditional Beliefs and Strategies
- Suppose you're at an information set; you don't know which of several nodes you might be at.
- How can you use what you know about other players' strategies to form beliefs about the true state of the world?
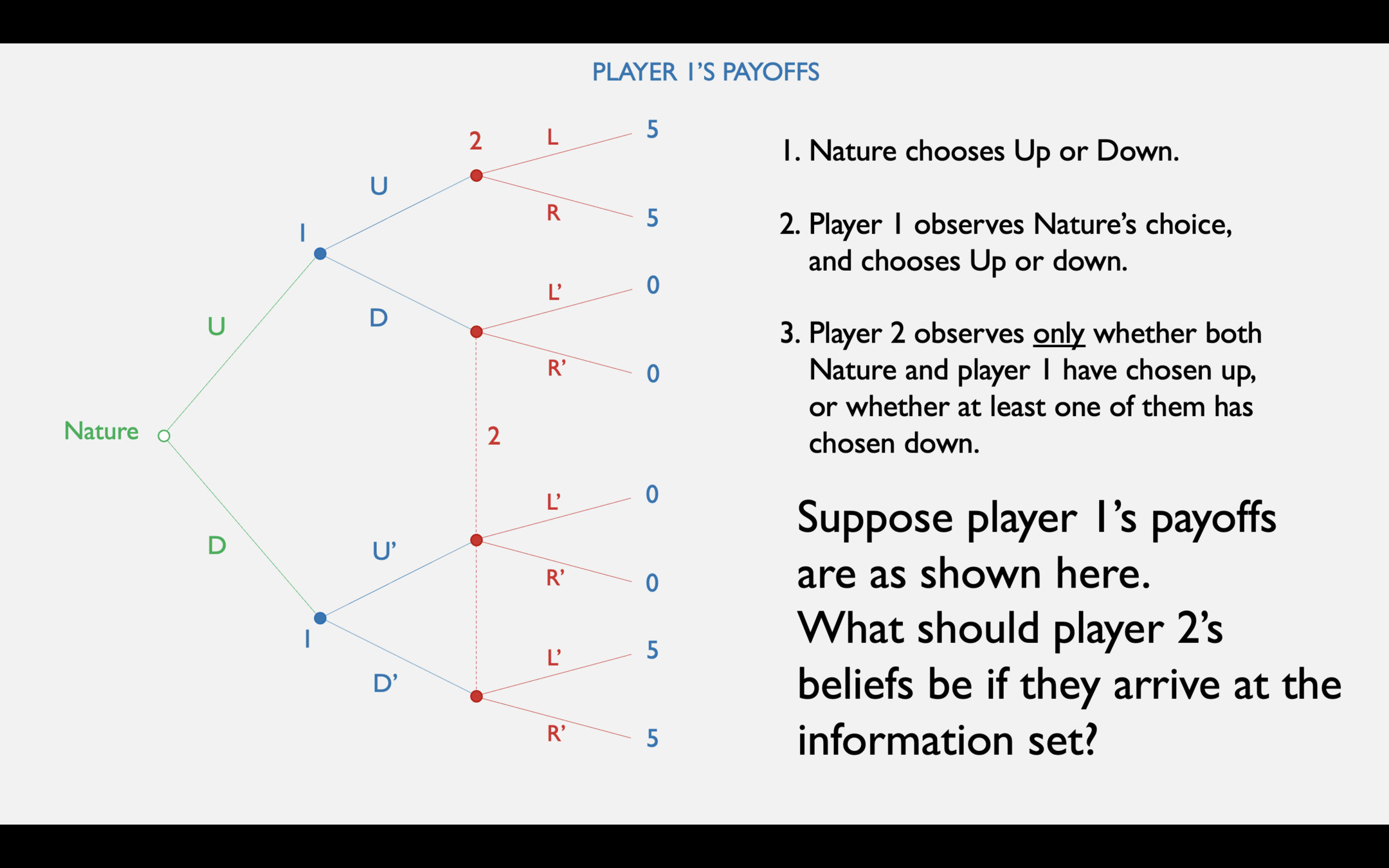
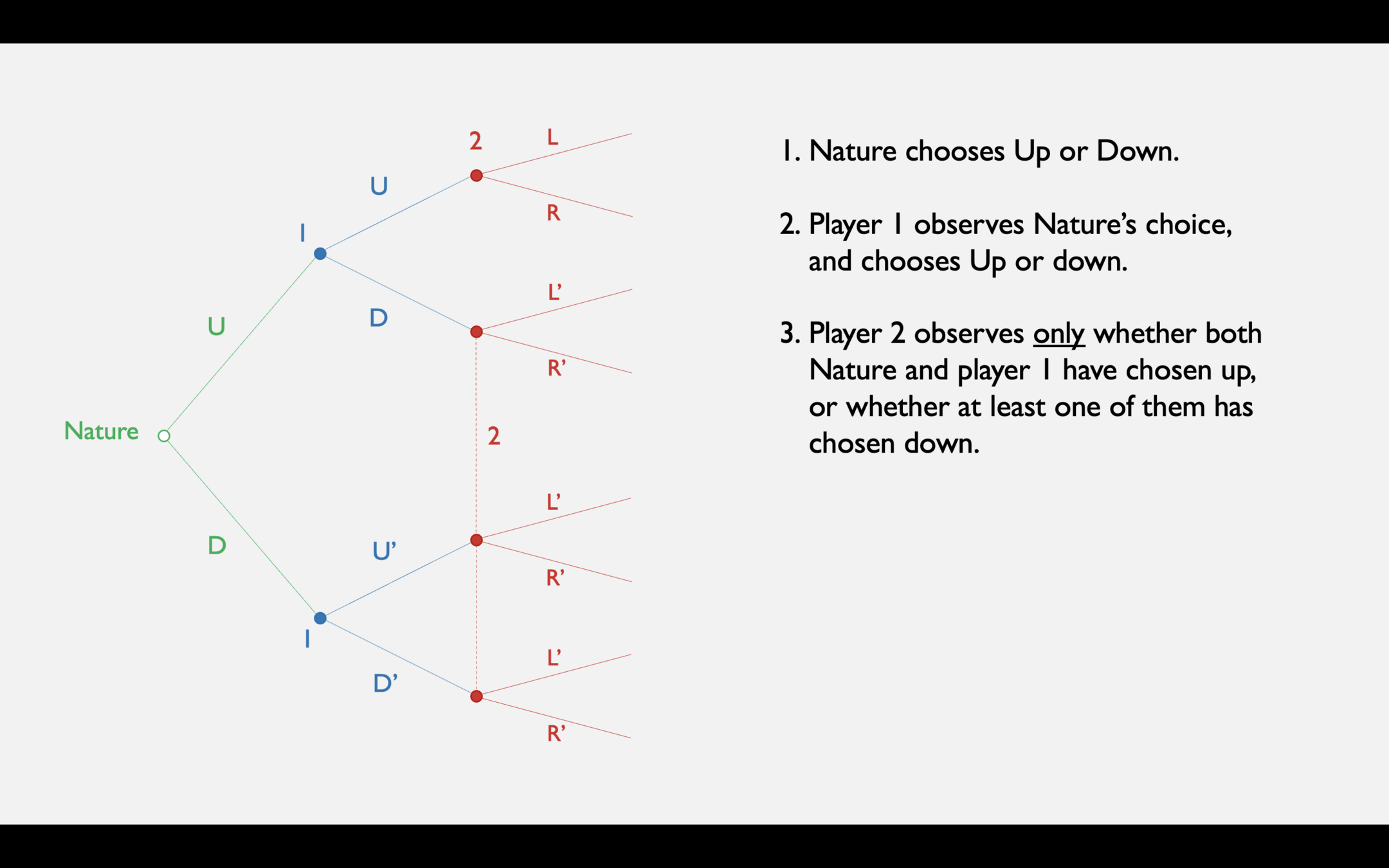
Perfect Bayesian Equilibrium
Consider a strategy profile for the players, as well as beliefs over the nodes at all information sets.
These are called a perfect Bayesian Equilibrium (PBE) if:
- Each player’s strategy is optimal to them at each infoset, given beliefs at this infoset and opponents’ strategies (“Sequential Rationality”)
- The beliefs are obtained from strategies using Bayes’ Rule wherever possible (i.e. at each infoset that is reached with a positive probability) (“consistency of beliefs”)
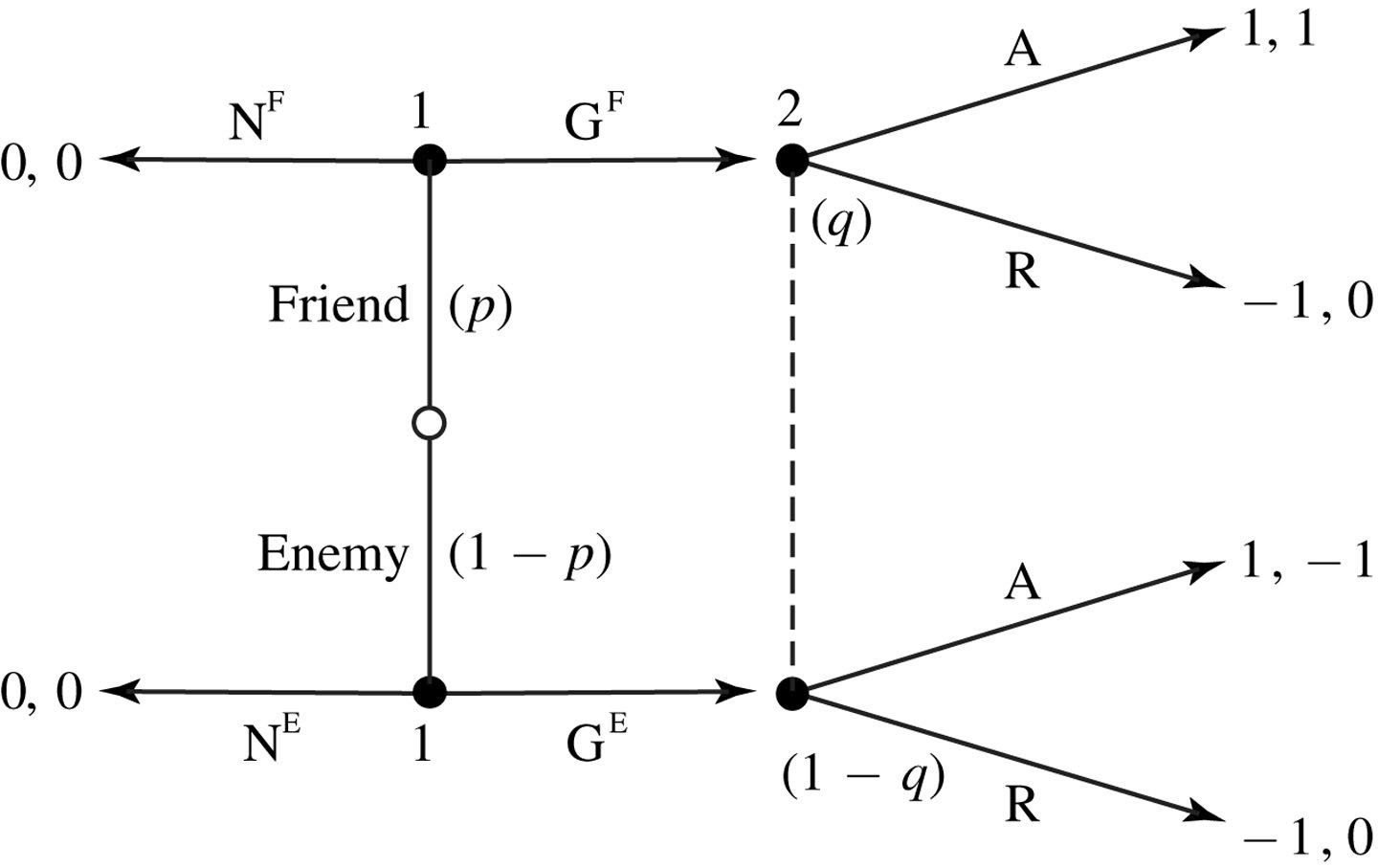
"Gift Giving Game"
Nature determines whether player 1 is a "friend" or "enemy" to player 2.
Player 1, knowing their type, can decide to give a gift to player 2 or not.
If player 1 gives a gift, player 2 can choose to accept it or not. Player 2 wants to accept a gift from a friend, but not from an enemy.
Whenever a player reaches an information set, they have some updated beliefs over which node they are.
Based on these beliefs, they should choose the action that maximizes their expected payoff.

"Gift Giving Game"
Nature determines whether player 1 is a "friend" or "enemy" to player 2.
Player 1, knowing their type, can decide to give a gift to player 2 or not.
If player 1 gives a gift, player 2 can choose to accept it or not. Player 2 wants to accept a gift from a friend, but not from an enemy.

"Gift Giving Game"
Nature determines whether player 1 is a "friend" or "enemy" to player 2.
Player 1, knowing their type, can decide to give a gift to player 2 or not.
If player 1 gives a gift, player 2 can choose to accept it or not. Player 2 wants to accept a gift from a friend, but not from an enemy.
In equilibrium, players' beliefs should be consistent with the strategies being played.
What is \(q\) if player 1 plays \(G^FN^E\)?
What is \(q\) if player 1 plays \(N^FG^E\)?
What is \(q\) if player 1 plays \(G^FG^E\)?
What is \(q\) if player 1 plays \(N^FN^E\)?
Separating and Pooling Equilibria
Separating Equilibrium: Each type of informed player chooses differently,
thereby conveying information about their type to the uninformed player
Pooling Equilibrium: Each type of informed player chooses the same,
thereby leaving the uninformed player with their prior belief.
Steps for calculating perfect Bayesian equilibria: Guess and Check!
- Start with a strategy for player 1 (pooling or separating).
- If possible, calculate updated beliefs (q in the example) by using Bayes’ rule.
In the event that Bayes’ rule cannot be used, you must arbitrarily select an updated belief; here you will generally have to check different potential values for the updated belief with the next steps of the procedure. - Given the updated beliefs, calculate player 2’s optimal action.
- Check whether player 1’s strategy is a best response to player 2’s strategy.
If so, you have found a PBE.
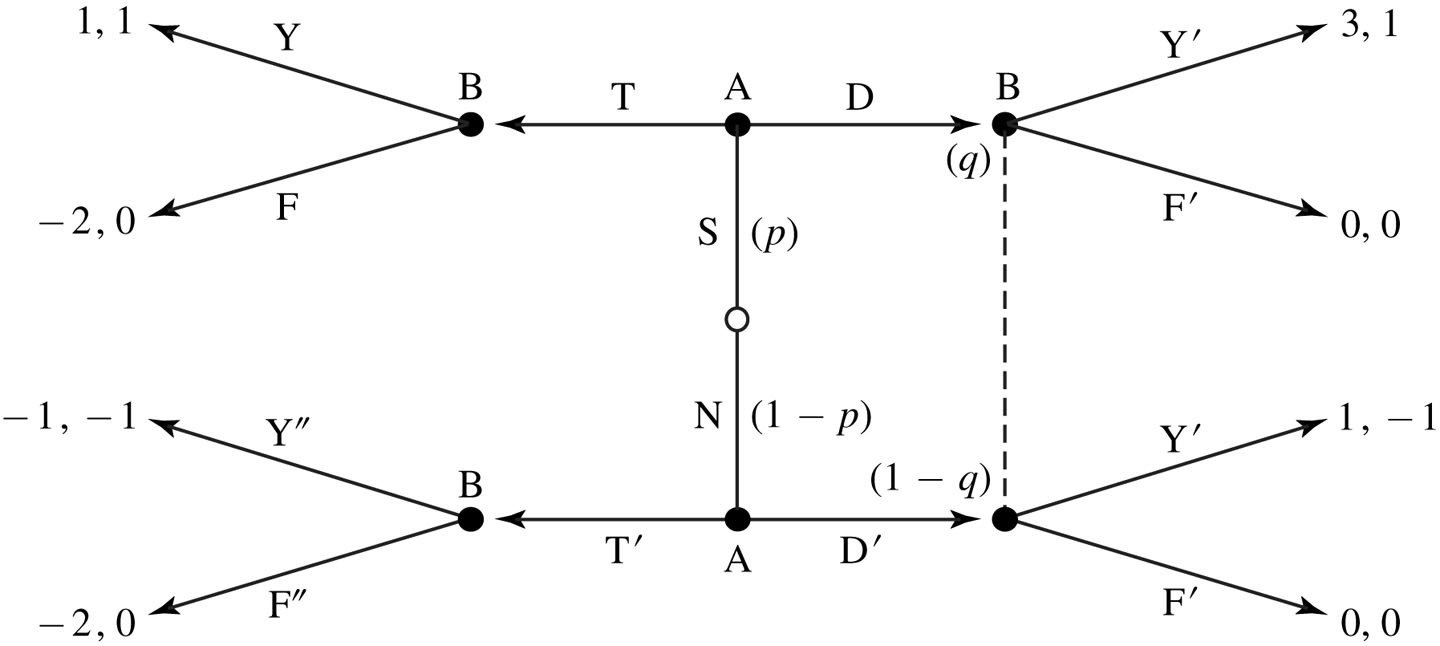
Guided Exercise from Watson (p. 385)