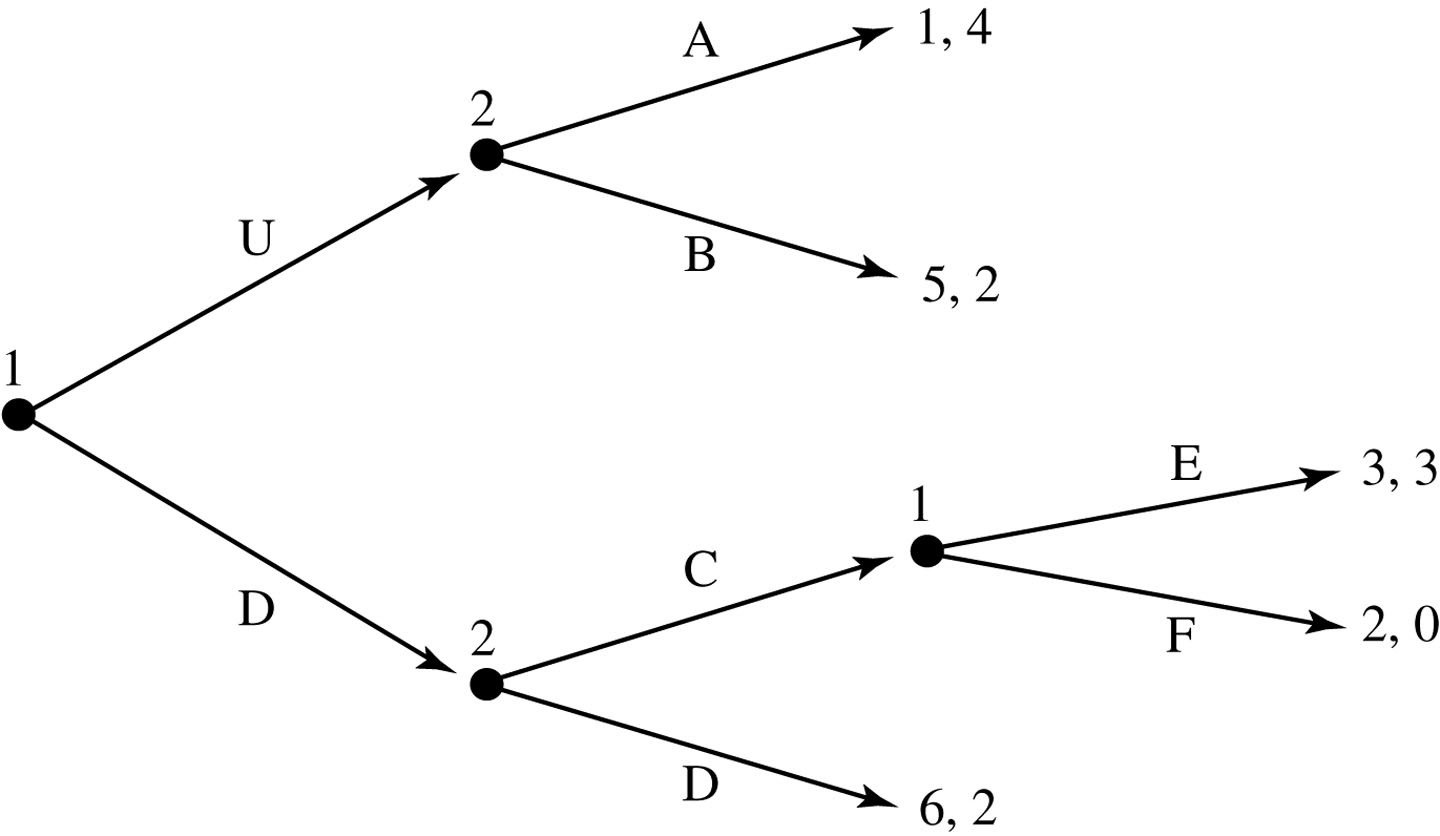
What is player 2's strategy space?
pollev.com/chrismakler


What is player 1's strategy space?
pollev.com/chrismakler

Dynamic Games and Subgame Perfection
Christopher Makler
Stanford University Department of Economics
Econ 51: Lecture 5
Golden Balls
How did Nick get Ibrahim to avoid getting stuck in the "prisoners' dilemma"?
Today's Agenda
Part 1: Discrete Strategies
Part 2: Continuous Strategies
Review: Extensive Form Games
Backward Induction
Strategies in Extensive Form Games
Subgame Perfect Nash Equilibrium
Example: Entry Deterrence
Example: Ultimatum Game
Example: Stackelberg Duopoly
Big Ideas
Credibility: can you credibly threaten some retaliation, or promise
some reward, to get the other player to do something you want?
Finite vs. Infinite Time Horizon: Does the game end?
Subgames: games will have more than one move; we can break them
up and examine subgames which are like games-within-games.
Review: Extensive Form Games
Normal-Form vs. Extensive-Form Representations
The extensive-form representation
of a game specifies:
The normal-form representation
of a game specifies:
The strategies available to each player
The player's payoffs for each combination of strategies
The players in the game
When each player moves
The actions available to each player each time it's their move
The players in the game
The player's payoffs for each combination of actions
Big Ideas
Today: extend notion of best-response (Nash) equilibrium to the class of dynamic games with complete & perfect information.
"dynamic"
takes place over time;
not simultaneous/one-shot
"complete information"
all players know all relevant aspects of the game (especially payoffs)
"perfect information"
all players observe all moves
X
Y
A
B
3
2
1
0
2
0
1
3
C
D
1
2
2
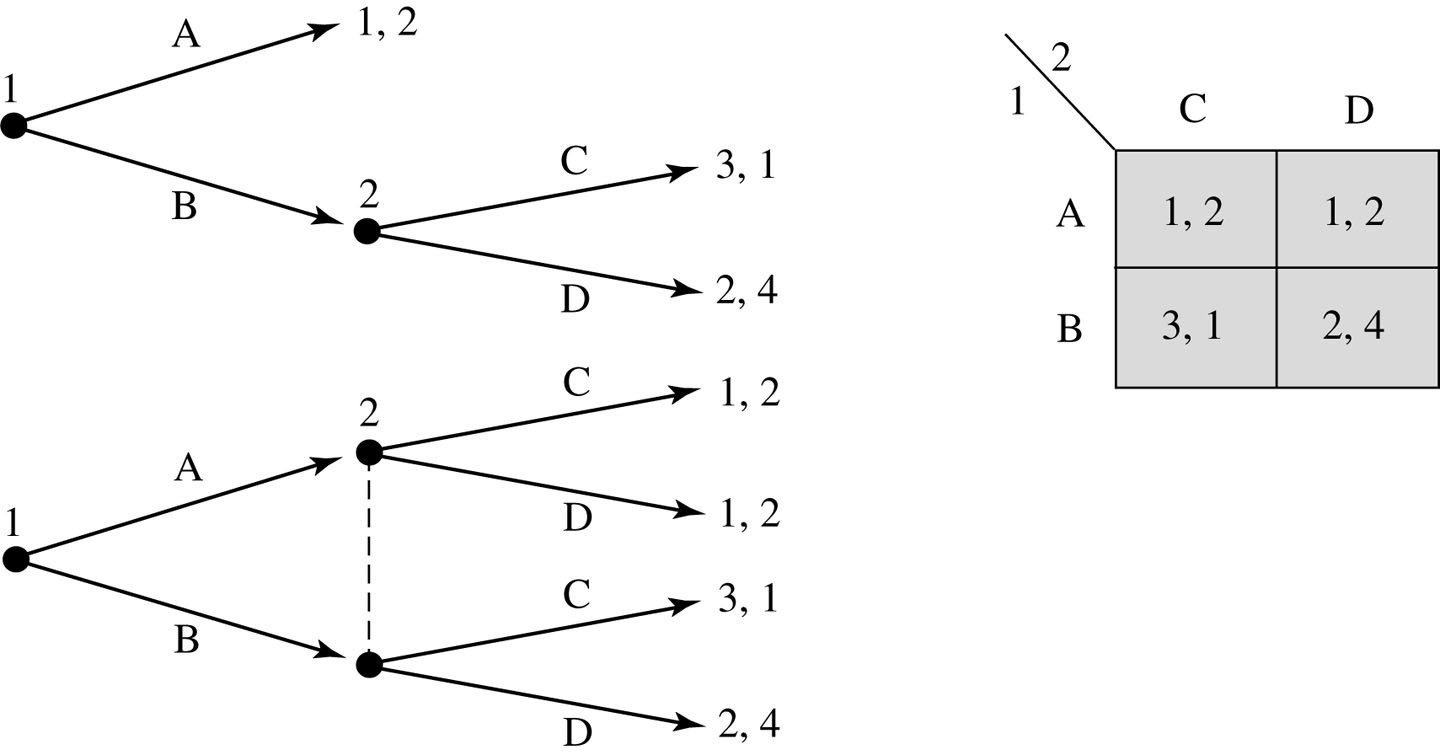
Consider the following game.
Player 1 starts.
She chooses X or Y.
Player 2 observes player 1's choice.
If player 1 chose X, player 2 chooses A or B.
If player 1 chose Y, player 2 chooses C or D.
After player 2 makes his choice, the payoffs to each player are realized.
"Play X."
"Play Y."
What is player 1's strategy space?
What is player 2's strategy space?
"Play A after X, and C after Y."
"Play A after X, and D after Y."
"Play B after X, and C after Y."
"Play B after X, and D after Y."
X
Y
A
B
3
2
1
0
2
0
1
3
C
D
1
2
2
X
Y
X
Y
A
B
3
2
1
0
2
0
1
3
C
D
1
2
2
What is player 1's strategy space?
What is player 2's strategy space?
AC
AD
BC
BD
1
2
X
Y
X
Y
A
B
3
2
1
0
2
0
1
3
C
D
1
2
2
AC
AD
BC
BD
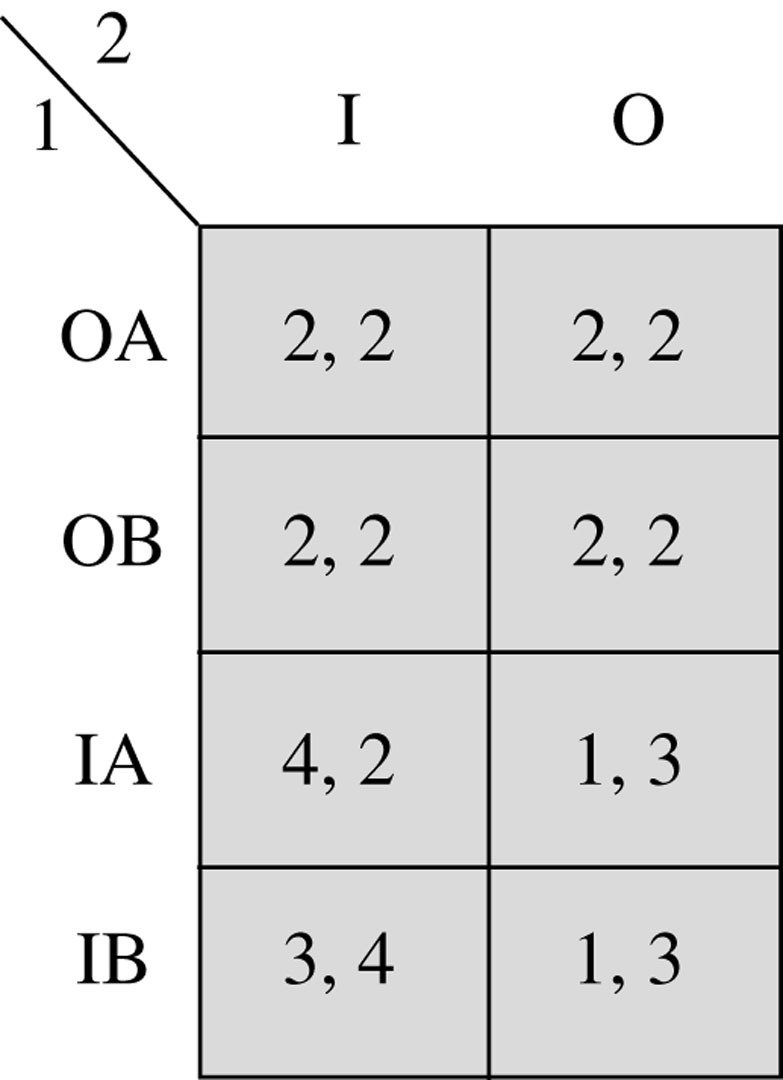
We can create the normal-form representation of this game.
3
2
1
0
2
0
1
3
3
2
1
3
2
1
0
0
1
2
X
Y
X
Y
A
B
3
2
1
0
2
0
1
3
C
D
1
2
2
AC
AD
BC
BD
We can create the normal-form representation of this game.
3
2
1
0
2
0
1
3
3
2
1
3
2
1
0
0
What are the Nash equilibria of this normal-form game?
Do any of the Nash equilibria not make sense?
1
2
X
Y
X
Y
A
B
3
2
1
0
2
0
1
3
C
D
1
2
2
AC
AD
BC
BD
3
2
1
0
2
0
1
3
3
2
1
3
2
1
0
0
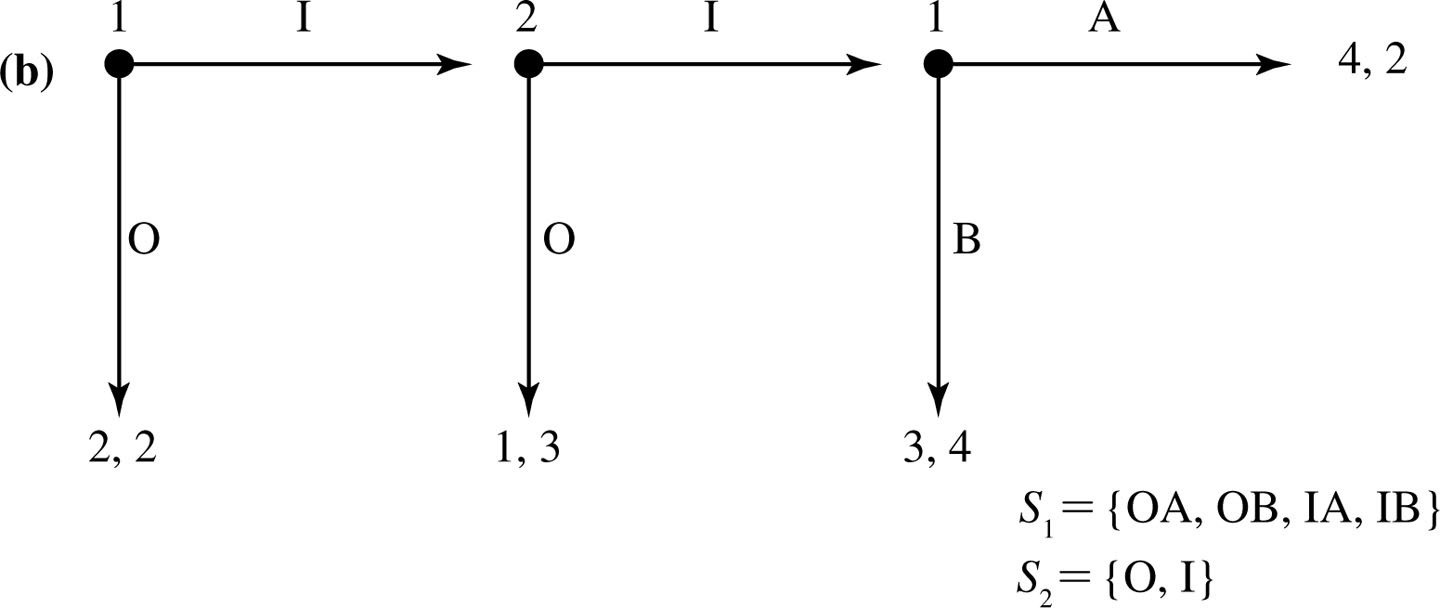
Think about this: after player 1 makes her move, we are in one of two subgames.
What should player 2 do in each subgame?
1
2
X
Y
X
Y
A
B
3
2
1
0
2
0
1
3
C
D
1
2
2
AC
AD
BC
BD
Think about this: after player 1 makes her move, we are in one of two subgames.
3
2
1
0
2
0
1
3
3
2
1
3
2
1
0
0
What should player 2 do in each subgame?
Anticipating how player 2 will react, therefore, what will player 1 choose?
1
2
X
Y
X
Y
A
B
3
2
1
0
2
0
1
3
C
D
1
2
2
AC
AD
BC
BD
Think about the other Nash equilibrium.
3
2
1
0
2
0
1
3
3
2
1
3
2
1
0
0
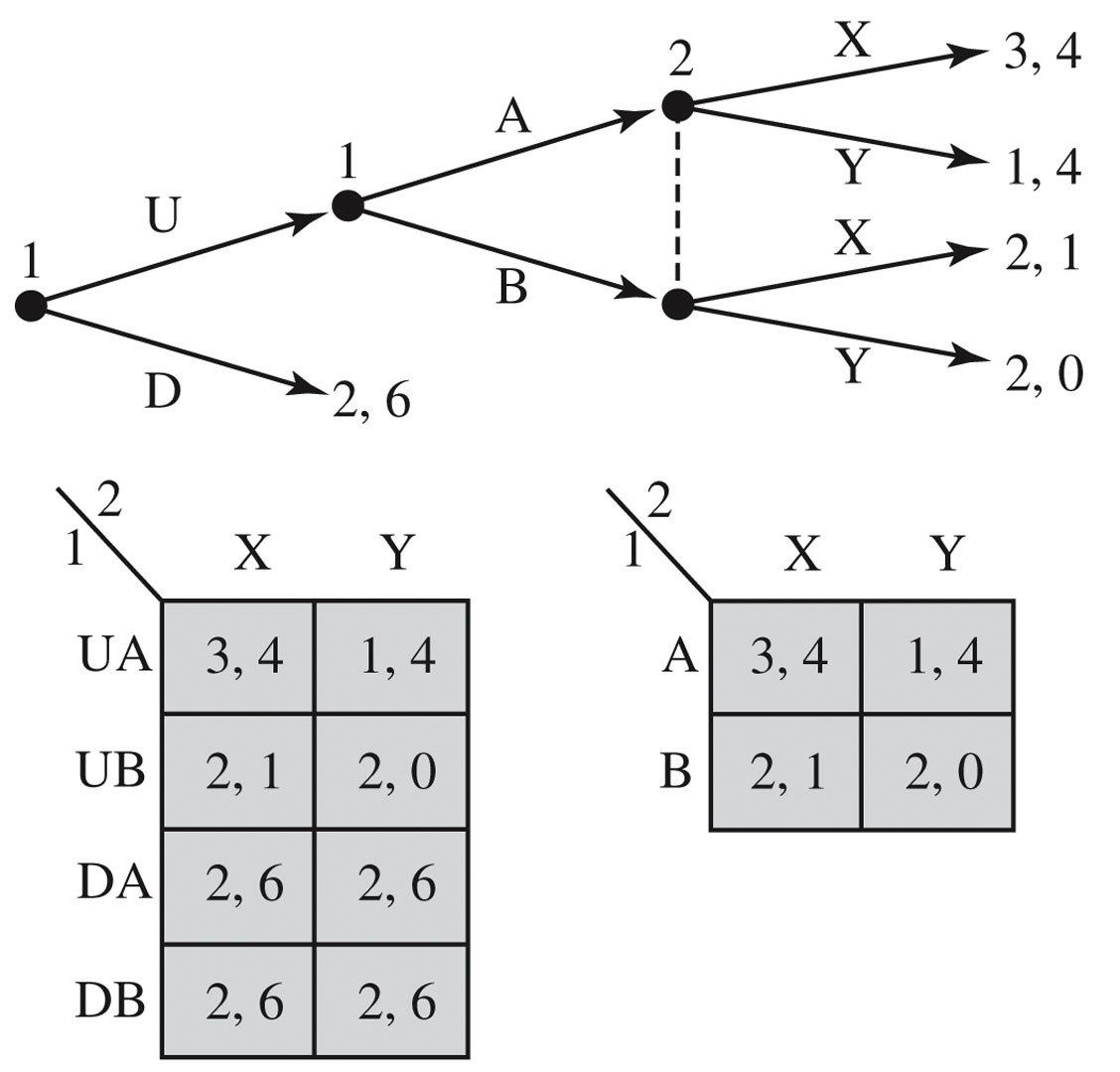
This is better for player 2.
It's kind of like player 2 is threatening to play D if player 1 chooses Y.
But this threat is not credible.
Definition: Subgame Perfect Nash Equilibrium
In an extensive-form game of complete and perfect information,
a subgame in consists of a decision node and all subsequent nodes.
A Nash equilibrium is subgame perfect if the players' strategies
constitute a Nash equilibrium in every subgame.
(We call such an equilibrium a Subgame Perfect Nash Equilibrium, or SPNE.)
Informally: a SPNE doesn't involve any non-credible threats or promises.
Another Example: Entry Deterrence
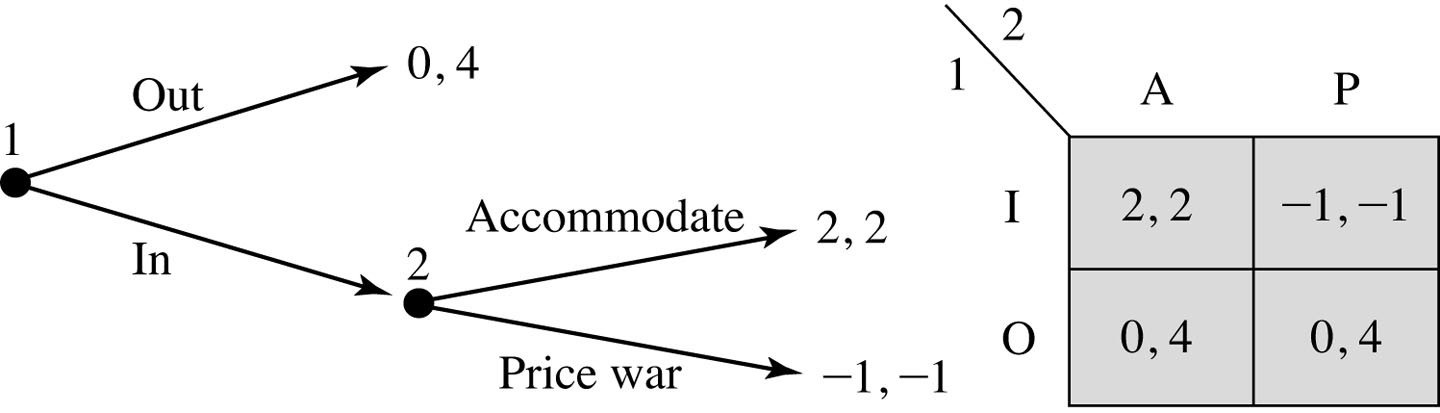
What are the subgames of this game?


What are the subgames of this game?


What are the subgames of this game?

Backwards induction is a method of determining the outcome(s) of a game by starting at the end and working backwards.
Finite games: start from terminal nodes
Infinite games: a bit more complicated
A Subgame Perfect Nash Equilibrium must specify a NE in every subgame!
Continuous Strategies
How do we represent a continuous strategy in an extensive-form game?
(For example, the quantity chosen by a firm in a Cournot-like game?)
Quantity Duopoly
- Two firms ("duo" in duopoly)
- Each chooses how much to produce
- Market price depends on
the total amount produced - Each firm faces a residual demand curve
based on the other firm's choice
Players: Two firms, Firm 1 and Firm 2
Payoffs:
Market price is determined by total output produced
Profit to Firm 2:
Profit to Firm 1:
New twist:
Firm 1 chooses \(q_1\) first;
Firm 2 observes \(q_1\) and chooses \(q_2\)
What are the strategy spaces?
Example: Stackelberg Duopoly
Stackelberg Model
- Firm 1 chooses how much to produce first \(q_1\),
at a cost of $2 per unit - Firm 2 observes firm 1's choice,
and then chooses how much to produce \(q_2\),
also at a cost of $2 per unit - The market price is determined by \(P(q_1,q_2) = 14 - (q_1+q_2)\)
- Profits are realized
- \(\pi_1(q_1,q_2) = (14 - [q_1 + q_2]) \times q_1 - 2q_1\)
- \(\pi_2(q_1,q_2) = (14 - [q_1 + q_2]) \times q_2 - 2q_2\)
What is firm 2's optimal strategy,
having observed \(q_1\)?
2
P
"Firm 2's Residual Demand Curve"
This function is firm 2's strategy.
It specifies what firm 2 will do after every possible move of firm 1.
What is firm 1's best response to firm 2's strategy of \(q_2^*(q_1)\)?
Firm 2's strategy:
Stackelberg Equilibrium
Firm 2's strategy: whatever \(q_1\) firm 1 produces, produce \(6 -{1 \over 2} q_1\) (or 0)
Firm 1's strategy: produce 6 units of output
Given what the other firm is doing, does either firm
have any incentive to change its strategy?
In equilibrium, firm 2 produces 3 units.
Why don't we just say that its strategy is "produce 3 units of output"?
Consider the following strategy for firm 2:
"You should produce the Cournot quantity of 4.
If you do, I'll also produce 4.
If you don't, I'll produce so much that the price is 2,
so we both sell at marginal cost and nobody makes a profit."
What is firm 1's best response to this strategy?
Summary & Next Steps
- Today we saw that some Nash Equilibria are not subgame perfect.
- Next time, we'll look at a special kind of dynamic game: repeated games.
- We'll show that playing a repeated game enables us to have outcomes
that are not Nash equilibria of the one-shot game - In particular, we'll show that we can sustain cooperation in
Prisoners' Dilemma type games if players have an ongoing relationship
(are playing an infinitely repeated game)