Nash Equilibrium

To navigate: press "N" to move forward and "P" to move back.

To see an outline, press "ESC". Topics are arranged in columns.

Today's Agenda

Part 1: Discrete Strategies

Part 2: Continuous Strategies

Nash Equilibrium

Mixed-Strategy Nash Equilibrium

Baseline Case: Monopoly

Quantity Choice: Cournot

Location Choice: Median Voter Theorem

Nash Equilibrium

Definition: Nash Equilibrium

A strategy profile in which every player
is playing a best response to the strategies played by the other players.

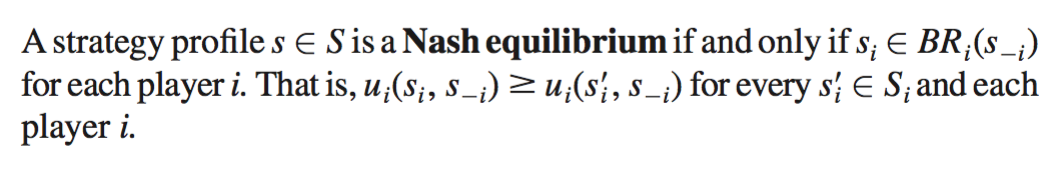
Wait a Second!

Chapter 6:

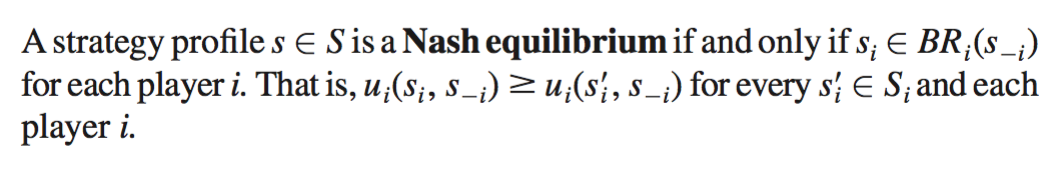
Chapter 9:

BR is a function of beliefs about strategies

BR is a function of strategies (not beliefs)

What happened in that sea of text between these two definitions?

We made the assumption that beliefs are accurate.

Recall: Strategic Uncertainty

When I didn't let the players talk,
both of them chose Hare.

What if I let them talk?

Possible rationales for strategic certainty:

  • People play this game all the time, and reasonably expect
    the other player to play according to the equilibrium.
  • The players have agreed on a strategy before the game is played;
    as long as no one has an incentive to deviate, it's OK.
  • An outside mediator (society, the law) recommends a strategy profile

Example: Party or Not?

Players: Two friends, Veronica and Heather

Strategy Spaces: {"Party", "Stay In"}

Payoffs:

Both would rather do what the other is doing

Both would rather go to the party

Stay In

Party

Party

Stay In

Heather

Veronica

2

2

0

0

0

0

1

1

("Pareto Coordination" game)

Players: Two friends, Chris and Pat

Strategy Spaces: {"Opera", "Fight"}

Payoffs:

They each get no payoff if they don't go to the same place.

Chris gets a higher payoff if they both go to the opera

Pat gets a higher payoff if they both go to the prize fight

Fight

Opera

Opera

Fight

Pat

Chris

2

1

0

0

0

0

1

2

Example: Opera or Prize Fight

("Battle of the Sexes" game)

Third Strategic Tension:
Inefficient Coordination

Recall: Party or Not?

Players: Two friends, Veronica and Heather

Strategy Spaces: {"Party", "Stay In"}

Payoffs:

Both would rather do what the other is doing

Both would rather go to the party

Stay In

Party

Party

Stay In

Heather

Veronica

2

2

0

0

0

0

1

1

("Pareto Coordination" game)

Dvorak vs QWERTY

Players: Companies buying computer keyboards

Strategy Spaces: {"Dvorak", "QWERTY"}

Payoffs:

Both would rather do what the other is doing (so new workers can type)

Both would rather use Dvorak (workers more productive)

QWERTY

Dvorak

Dvorak

QWERTY

2

2

0

0

0

0

1

1

Mixed-Strategy Nash Equilibrium

Example: Matching Pennies (Zero-sum game)

Players: Two bettors, Ros and Guil

Strategy Spaces: {"Heads", "Tails"}

Payoffs:

If they're both the same, Ros wins

If they're different, Guil wins

Tails

Heads

Heads

Tails

Guil

Ros

1

-1

-1

1

-1

1

1

-1

There is no pure-strategy equilibrium.
Is there an equilibrium in mixed strategies?

If Guil plays H with probability \(q\), what is Ros's payoff to playing H? To playing T?

What is Ros's best response to Guil playing the mixed strategy \((q, 1-q)\)?

What, therefore, is Guil's best response to Ros playing the mixed strategy \((p, 1-p)\)?

What equilibrium exists in which both players are best responding to one another?

If a player is to play a mixed strategy, they must be indifferent between all the strategies to which they assign positive probability.

Key Insight

Tennis!

F = forehand

C = center

B = backhand

Server: player 1

Returner: player 2

Continuous Strategies

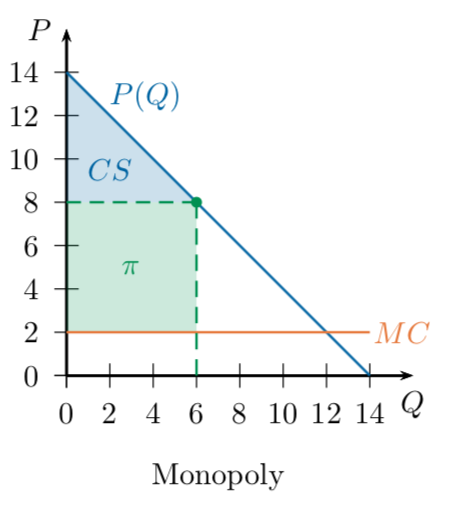
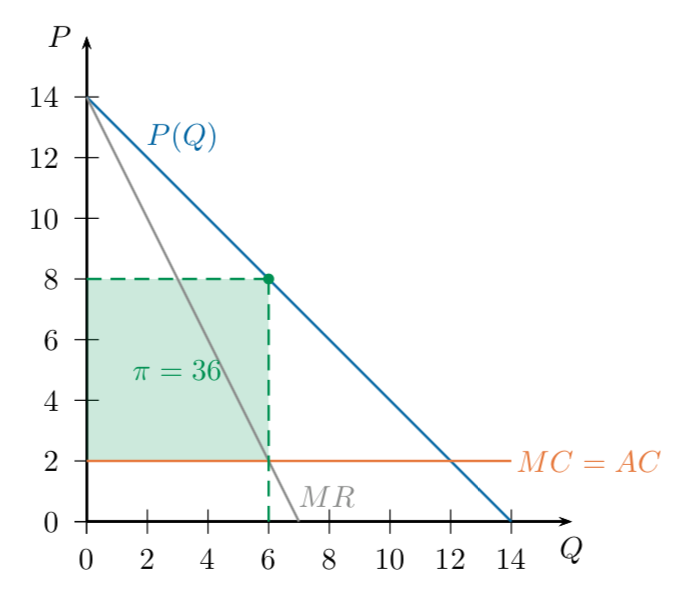
Baseline Case: Monopoly

A single-price monopolist faces an inverse demand curve P(Q)
which determines the market price if it produces Q units of output.

The monopolist's profit-maximization problem is to choose Q to maximize:

\pi(Q) = P(Q)Q -c(Q)

Maximize by taking the derivative and setting equal to zero.

\text{total revenue}
\text{total cost}
P(Q) = 14 - Q
c(Q) = 2Q
\text{Market Demand:}
\text{Monopoly's Costs: }

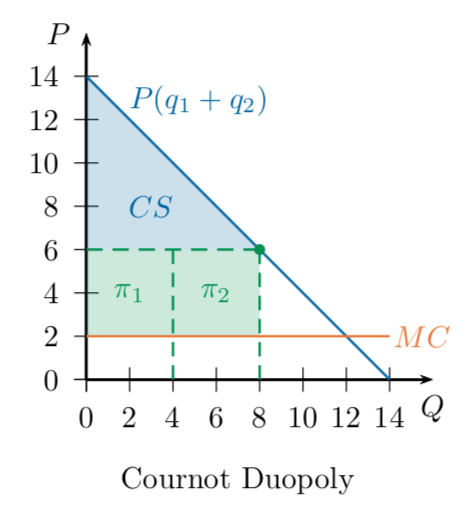
Quantity Choice: Cournot Duopoly

c_1(q_1) = 2q_1
c_2(q_2) = 2q_2
\text{Firm 1's Costs:}
\text{Firm 2's Costs:}

Cournot (Quantity) Duopoly

Players: Two firms, Firm 1 and Firm 2

Strategy Spaces: each firm chooses a level of output \(q_i\)

Outcome:

Market price is determined by total output produced:

Profit to each firm is

P(q_1,q_2)
\pi_i(q_i,q_{-i}) = P(q_i,q_{-i})q_i - c_i(q_i)

Payoffs:

P(Q) = 14 - Q
\text{Market Demand:}

Best-Response Functions

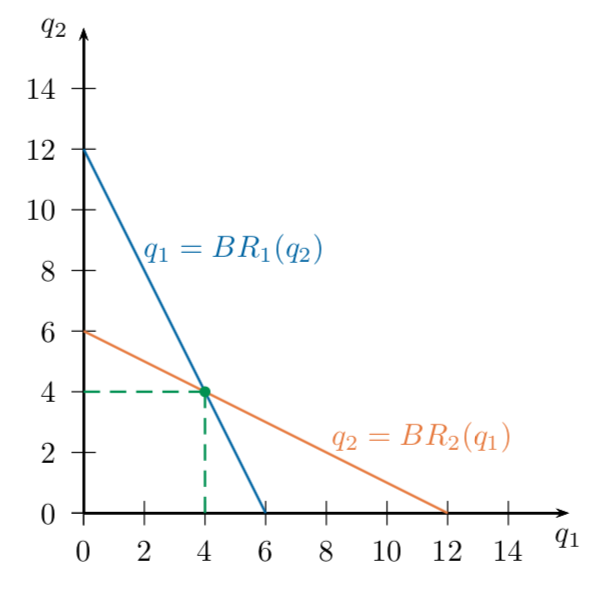
What is the Nash Equilibrium of this game?

P = 8, Q = 6
CS = 18
\pi = 36
P = 6, Q = 8
CS = 32
\pi_1 = \pi_2 = 16
P = 2, Q = 12
CS = 72
\sum \pi = 0