Repeated Games
To navigate: press "N" to move forward and "P" to move back.
To see an outline, press "ESC". Topics are arranged in columns.
Today's Agenda
Part 1: Discrete Strategies
Part 2: Continuous Strategies
Finitely Repeated Games
Evaluating Infinite Payoffs
Infinitely Repeated Games
Sustaining Collusion in a Cournot Duopoly
Finitely Repeated Games
Suppose there is some stage game G, which is repeated for T periods,
with the payoffs being the sum of the payoffs in each period.
Trivial result: it is always a SPNE if a NE is played in every period.
Nontrivial result: there may be SPNE in which non-NE strategy profiles are played in early periods.
Key insight: this requires multiple Nash equilibria, which gives the ability to credibly promise a reward in the last period.


Evaluating Infinite Payoffs
Value of getting payoff \(x\) forever, starting today:
Value of getting payoff \(z\) forever, starting tomorrow:
Value of getting payoff \(y\) today and then payoff \(z\) tomorrow and forever after:
Infinitely Repeated Games
Strategy in a Repeated Game
- Must specify what to do in each period,
as a function of all previously taken actions. - We often group action histories to make strategies simpler:
- Grim trigger: "If anyone has ever played 'cheat'"
- Tit-for-tat: "If the other player played 'cheat' last period"
- Limited punishment: "If the other player played 'cheat' in any of the last 3 periods"
Cooperate
Defect
Cooperate
Defect
2
3
0
1
2
1
0
3
Suppose the following prisoner's dilemma is repeated indefinitely,
with future payoffs discounted at rate \(\delta < 1\).
Consider the grim trigger strategy: "If you ever defect, I will defect for all eternity." For what values of \(\delta\) would that constitute a SPNE?
Sustaining Collusion
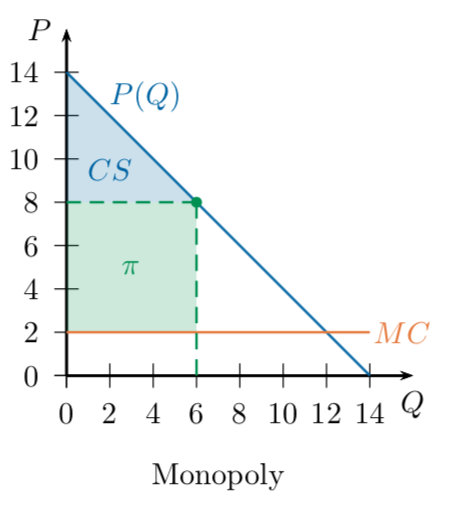
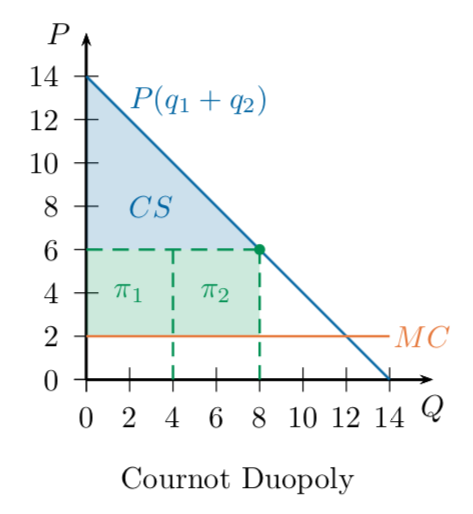
Recall from last time: market demand \(P(Q) = 14 - Q\),
all firms have constant MC of 2
Monopoly: produces 6, profit of 36
Cournot equilibrium: each firm produces 4, receives profit of 16
Possible collusion: each firm produces 3, receives profit of 18
Best possible deviation: if the other firm produces 3,
produce 4.5, receive payoff of 20.25.
If the other firm is playing a grim trigger strategy,
what's your payoff from colluding and producing 3? From deviating and producing 4.5?
Cournot (Quantity) Duopoly
Players: Two firms, Firm 1 and Firm 2
Strategy Spaces: each firm chooses a level of output \(q_i\)
Outcome:
Market price is determined by total output produced:
Profit to each firm is
Payoffs:
Could the two firms do better than Cournot?
Payoff from Colluding
Payoff from most profitable defection
Assume the other player is playing the grim trigger strategy:
"I will collude and play 3 as long as you collude and play 3.
If anyone has ever defected and not played 3, I will play the Cournot quantity of 4 forever."
Conclusions and Next Steps
Last time we saw that not all Nash equilibria involve credible threats.
This time we saw that playing games over time allows credible threats that
sustain non-Nash behavior in each period (i.e., can solve the prisoner's dilemma)
Playing games over time allows us to consider a wide range of strategies, including threats and promises about future behavior.
Next week: we introduce information problems.
What if you don't know the other players' true payoffs?
What if one player knows more than the other?
Can they credibly communicate their information?