Capsule Networks Introduction

Introduction Capsule Networks

1

Alexander Isenko

28.11.2017

In-House presentation @ iteratec

2

Alexander Isenko

28.11.2017

Motivation

Motivation

3

Alexander Isenko

28.11.2017

Default Graphics

Graphics

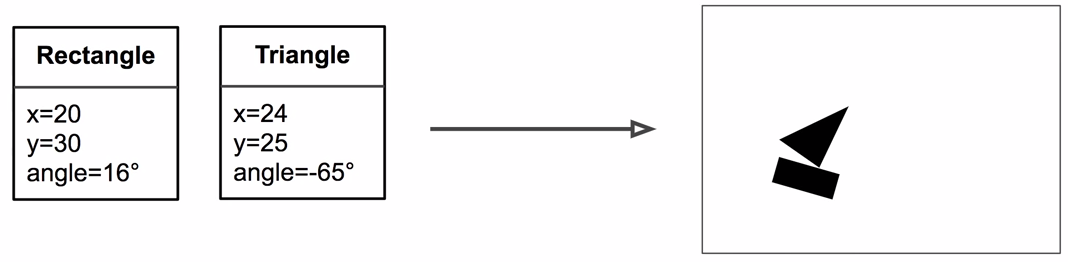
Instantiation Parameters

Rendering

Image

4

Alexander Isenko

28.11.2017

Inverse Graphics

Graphics

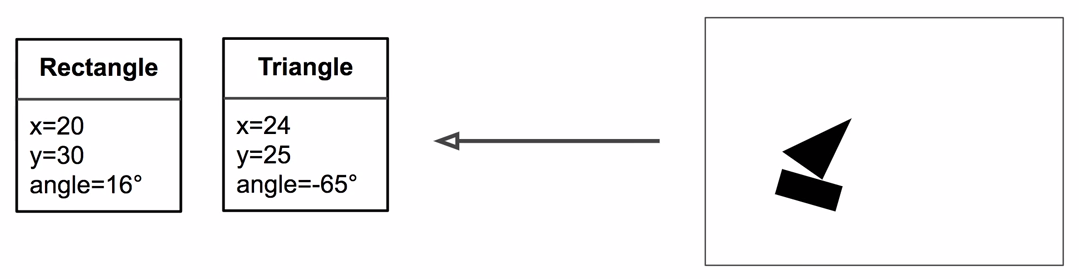
Instantiation Parameters

Inverse Rendering

Image

5

Alexander Isenko

28.11.2017

Capsule Activations

Capsules

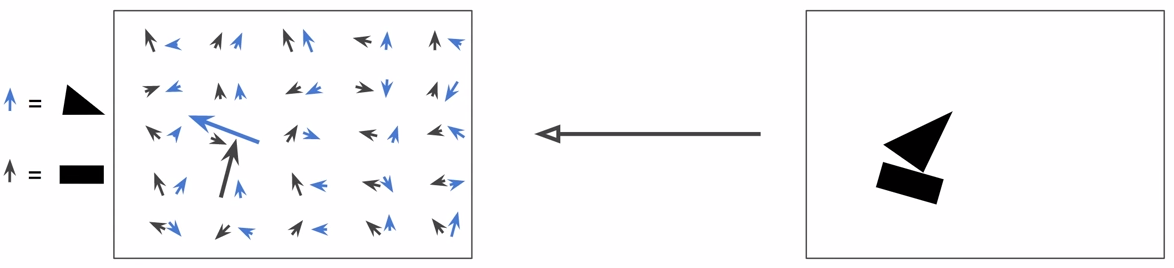
Capsule Activations

Image

Activation vector:

Length = estimated probability of presence

Orientation = estimated pose parameteres

1

Alexander Isenko

28.11.2017

Capsule Activations

Capsules

Capsule Activations

Image

Squash(\textbf{u}) =

Squash(\textbf{u}) =

\frac{||\textbf{u}||^2}{1 + ||\textbf{u}||^2} \cdot \frac{\textbf{u}}{ ||\textbf{u}||}

\frac{||\textbf{u}||^2}{1 + ||\textbf{u}||^2} \cdot \frac{\textbf{u}}{ ||\textbf{u}||}

Convolutional Layers

+ Reshape

+ Squash

6

Alexander Isenko

28.11.2017

Transformation Matrix

Capsules

\hat{\textbf{u}}_{j|i} = \textbf{W}_{ij}\textbf{u}_i

\hat{\textbf{u}}_{j|i} = \textbf{W}_{ij}\textbf{u}_i

\text{Transformation Matrix } \textbf{W}

\text{Transformation Matrix } \textbf{W}

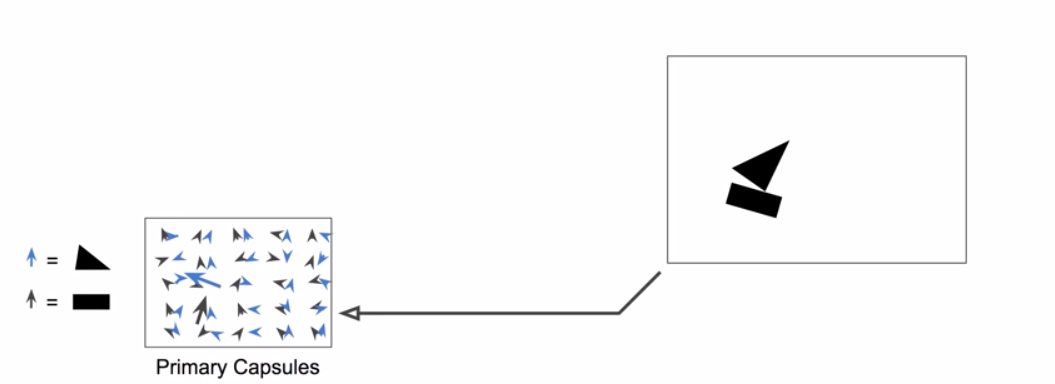
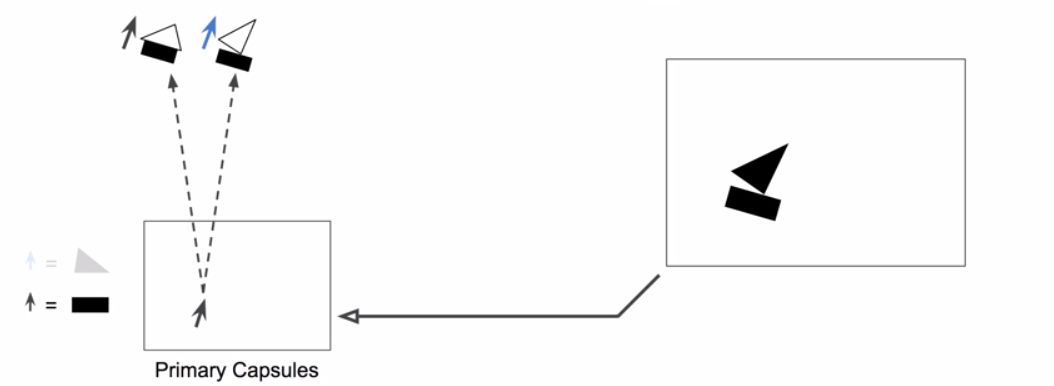
7

Alexander Isenko

28.11.2017

Routing by Agreement

Capsules

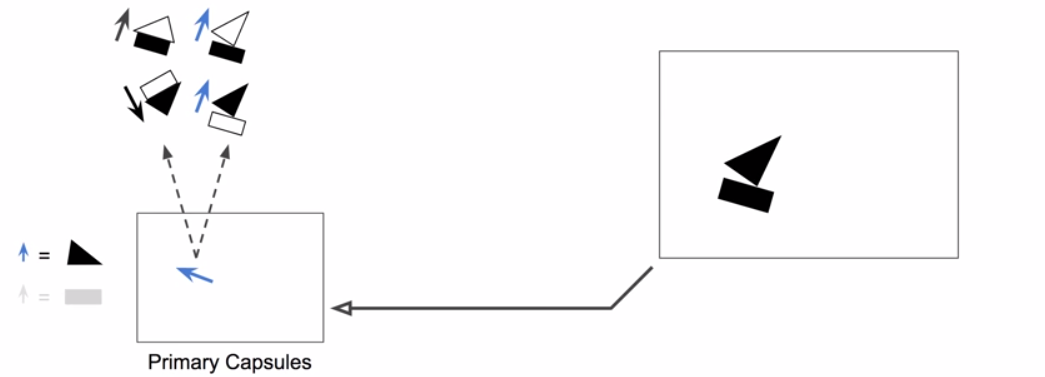
8

Alexander Isenko

28.11.2017

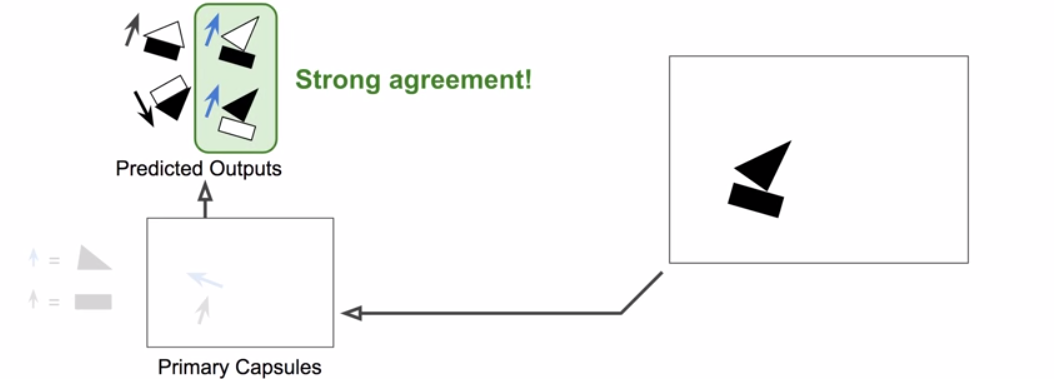
Routing by Agreement

Capsules

\forall i,j: b_{ij} = 0.5

\forall i,j: b_{ij} = 0.5

\textbf{c}_{i,j} = \text{softmax}(\textbf{b}_{i,j},\textbf{b}_{i} )

\textbf{c}_{i,j} = \text{softmax}(\textbf{b}_{i,j},\textbf{b}_{i} )

0.5

0.5

0.5

0.5

0.5

0.5

0.5

0.5

\hat{\textbf{u}}_{j | i}

\hat{\textbf{u}}_{j | i}

\hat{\textbf{u}}_{j | i}

\hat{\textbf{u}}_{j | i}

\textbf{s}_{i,j} = \textbf{c}_{i,j} \cdot

\textbf{s}_{i,j} = \textbf{c}_{i,j} \cdot

\textbf{v}_{j} = \text{squash}( \textbf{s}_{j})

\textbf{v}_{j} = \text{squash}( \textbf{s}_{j})

\textbf{b}_{i,j} \leftarrow \textbf{b}_{i,j} + \hat{\textbf{u}}_{j | i} \cdot \textbf{v}_{j}

\textbf{b}_{i,j} \leftarrow \textbf{b}_{i,j} + \hat{\textbf{u}}_{j | i} \cdot \textbf{v}_{j}

Final output of #1 round

Routing coefficient

Prediction vector

Routing weights

0.9

0.9

0.1

0.1

0.2

0.2

0.8

0.8

9

Alexander Isenko

28.11.2017

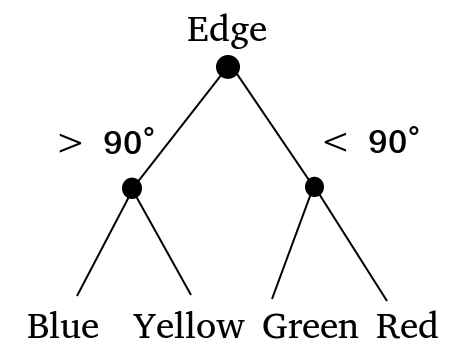
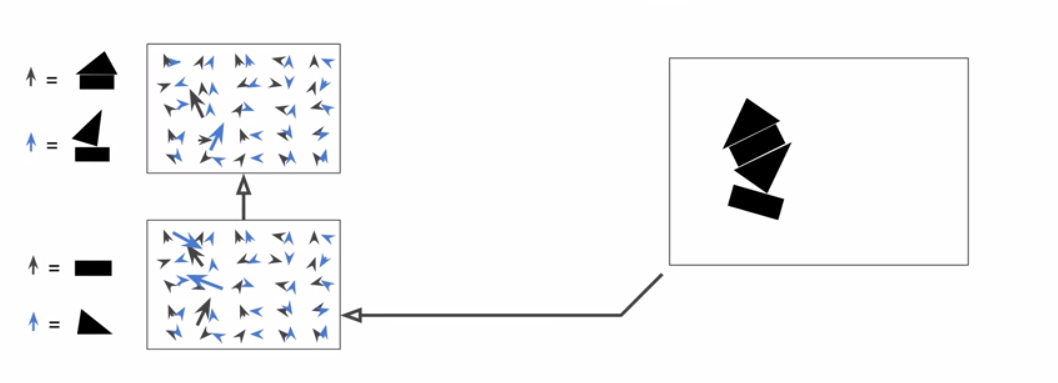
Crowded Scenes

Capsules

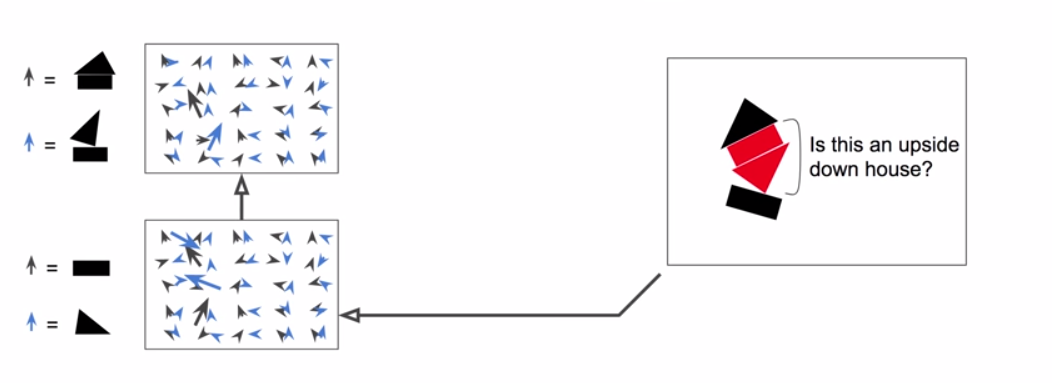
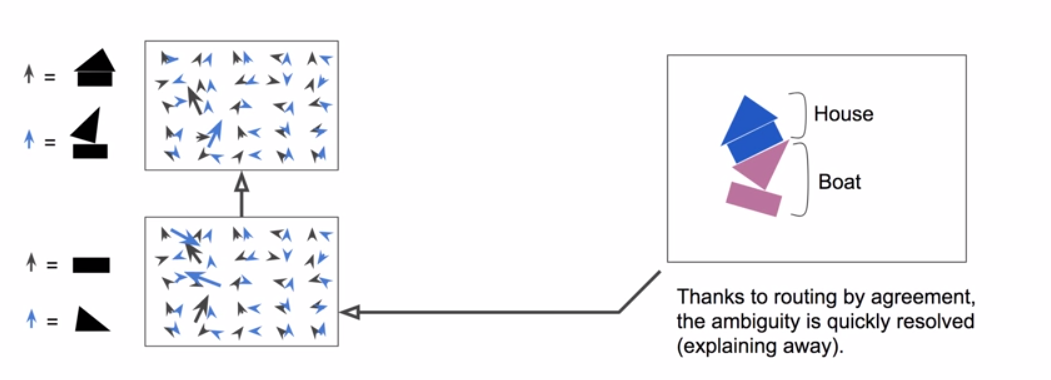
10

Alexander Isenko

28.11.2017

MNIST Classifier

Example

\textbf{Reconstruction} = 1, \textbf{Routing} = 1, \textbf{Error} = 0.29 \pm0.011

\textbf{Reconstruction} = 1, \textbf{Routing} = 1, \textbf{Error} = 0.29 \pm0.011

\textbf{Reconstruction} = 0, \textbf{Routing} = 3, \textbf{Error} = 0.35 \pm0.036

\textbf{Reconstruction} = 0, \textbf{Routing} = 3, \textbf{Error} = 0.35 \pm0.036

\textbf{Reconstruction} = 0, \textbf{Routing} = 1, \textbf{Error} = 0.34 \pm0.032

\textbf{Reconstruction} = 0, \textbf{Routing} = 1, \textbf{Error} = 0.34 \pm0.032

\textbf{Reconstruction} = 1, \textbf{Routing} = 3, \textbf{Error} = 0.25 \pm0.005

\textbf{Reconstruction} = 1, \textbf{Routing} = 3, \textbf{Error} = 0.25 \pm0.005

\textbf{Baseline} = 0.39

\textbf{Baseline} = 0.39

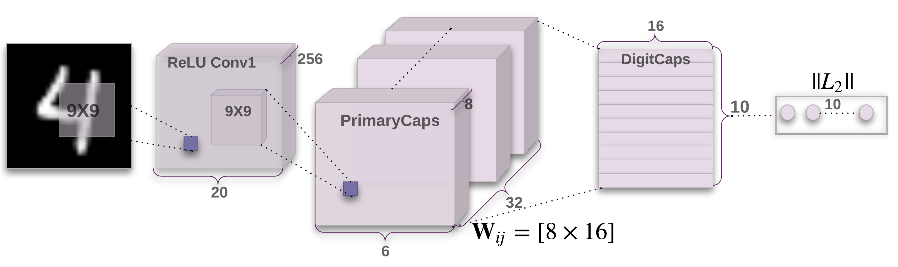
11

Alexander Isenko

28.11.2017

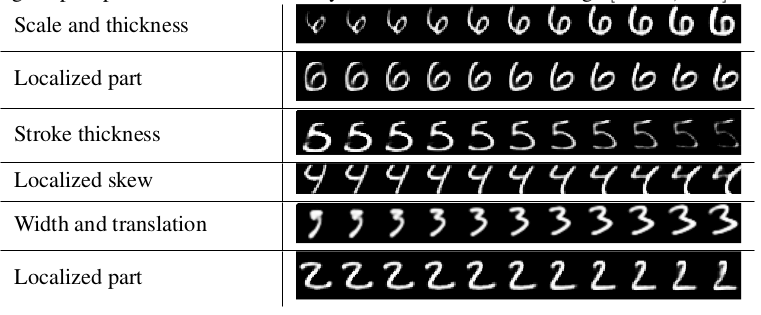
MNIST Latent Variables

Example

12

Alexander Isenko

28.11.2017

Takeaway

Pros

Routing by agreement is an innovative concept
- allows for better classification of crowded scenes
- does not throw away information in comp. to MaxPooling
Activation of the capsules is the vector length
Learning the transformation matrices
- scale, rotation
- not translation, that's via low level capsules (CNN)
Activation vectors are interpretable
- creation of hierarchy
Parse tree for "every fixation" point
Requires less data

13

Alexander Isenko

28.11.2017

Takeaway

Pros

\textbf{u}_{i}

\textbf{u}_{i}

\cdot \textbf{W}_{i,j}

\cdot \textbf{W}_{i,j}

\hat{\textbf{u}}_{j | i}

\hat{\textbf{u}}_{j | i}

\textbf{u}_{i}

\textbf{u}_{i}

=

=

\hat{\textbf{u}}_{j | i}

\hat{\textbf{u}}_{j | i}

= squash(\textbf{s}_j)

= squash(\textbf{s}_j)

\textbf{v}_{j}

\textbf{v}_{j}

Routing

Capsule

output

Routing coefficient

Capsule activation

Transformation Matrix

Prediction vector

c_{i,j}

c_{i,j}

\cdot \hat{\textbf{u}}_{j | i}

\cdot \hat{\textbf{u}}_{j | i}

\textbf{s}_j

\textbf{s}_j

\sum

\sum

\textbf{v}_j

\textbf{v}_j

14

Alexander Isenko

28.11.2017

Takeaway

CIFAR10 was not state of the art
Does it scale? Imagenet?
Slow training (routing agreement)
Can't see two close objects next to each other

Cons

15

Alexander Isenko

28.11.2017

Sources

Link to the original paper
Excellent youtube talk where I copied most of the slides
- Implementation links are provided in the description
A nice blog post