Bachelor Thesis

Neuroevolution in RoboCup2D

Bachelor Präsentation

1

Alexander Isenko

19.01.2017

Betreuer: Thomas Gabor M.Sc,

Dr. Lenz Belzner

3

Alexander Isenko

19.01.2017

Fragestellung

4

Alexander Isenko

19.01.2017

Fragestellung

5

Alexander Isenko

19.01.2017

Fragestellung

6

Alexander Isenko

19.01.2017

Fragestellung

Untersuchung von neuroevolutionären Algorithmen

in einer Domäne mit seltener Fitnessfunktion ohne Gradienten

7

Alexander Isenko

19.01.2017

Domäne - RoboCup [1][2]

RoboCup Small Size

RoboCup@Rescue

RoboCupSoccer Standart

RoboCupSoccer Humanoid

Untersuchung von neuroevolutionären Algorithmen in einer Domäne mit seltener Fitnessfunktion ohne Gradienten

8

Alexander Isenko

19.01.2017

Subdomäne - Half Field Offense

Halbes Spielfeld
1 vs 1 Szenario
Deterministischer Torwart

Untersuchung von neuroevolutionären Algorithmen in einer Domäne mit seltener Fitnessfunktion ohne Gradienten

9

Alexander Isenko

19.01.2017

Half Field Offense - Zustandsraum [3]

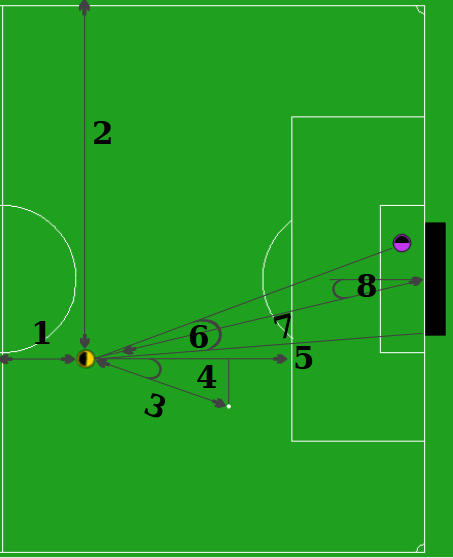
X-Position
Y-Position
Distanz zum Ball
Winkel zum Ball
Sichtrichtung
Winkel zw. Torwart & Pfosten
Distanz zur Tormitte
Winkel zur Tormitte
Ballaktion ausführbar

Untersuchung von neuroevolutionären Algorithmen in einer Domäne mit seltener Fitnessfunktion ohne Gradienten

10

Alexander Isenko

19.01.2017

Half Field Offense - Aktionsraum [3]

Aktion	Bedeutung
Move	Bewegung in Richtung des Balls
Shoot	Schieße den Ball in Richtung des Tores
Dribble	Schieße den Ball vor dir hin und lauf hinterher
Intercept	Sprintet in Richtung des Balls
No-Op	Führe keine Aktion aus

Untersuchung von neuroevolutionären Algorithmen in einer Domäne mit seltener Fitnessfunktion ohne Gradienten

11

Alexander Isenko

19.01.2017

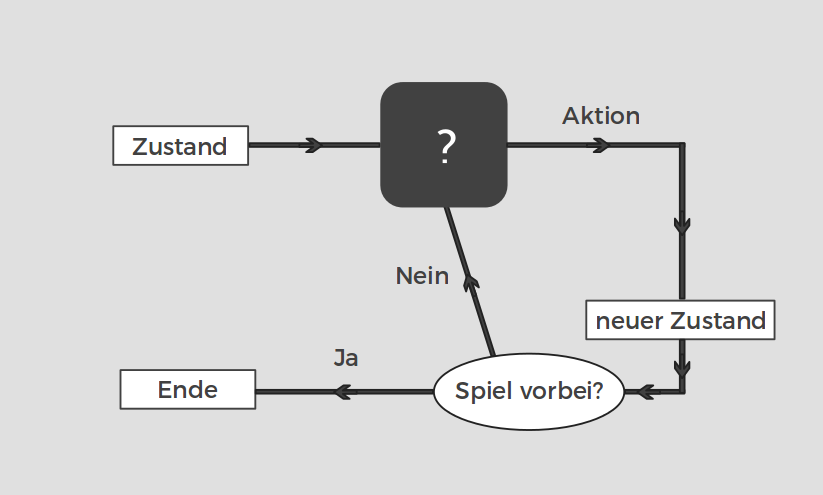
Half Field Offense - Ablauf eines Spiels

Untersuchung von neuroevolutionären Algorithmen in einer Domäne mit seltener Fitnessfunktion ohne Gradienten

12

Alexander Isenko

19.01.2017

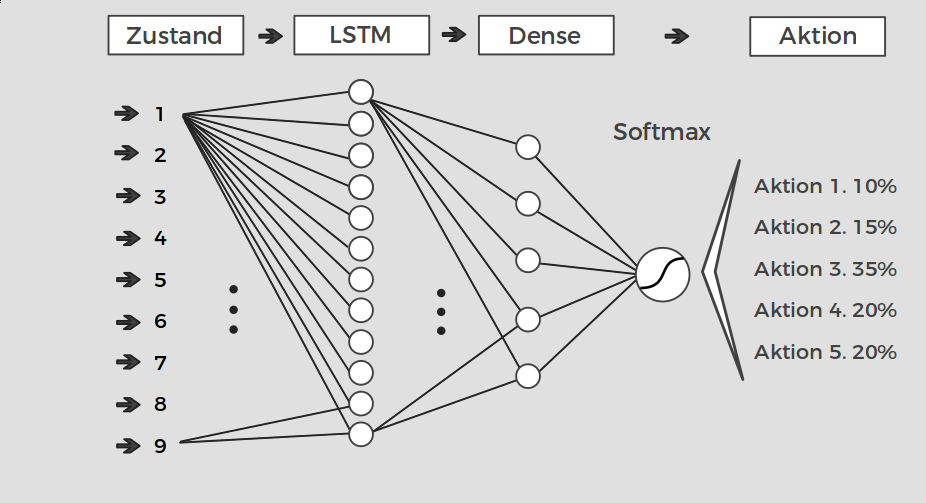
Technik - Neuronale Netze

Untersuchung von neuroevolutionären Algorithmen in einer Domäne mit seltener Fitnessfunktion ohne Gradienten

13

Alexander Isenko

19.01.2017

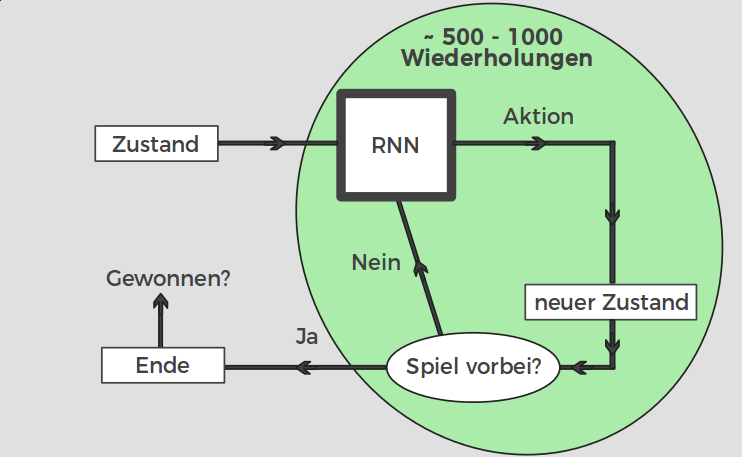
Problem - Seltene Fitnessfunktion

Untersuchung von neuroevolutionären Algorithmen in einer Domäne mit seltener Fitnessfunktion ohne Gradienten

14

Alexander Isenko

19.01.2017

Technik - Genetischer Algorithmus

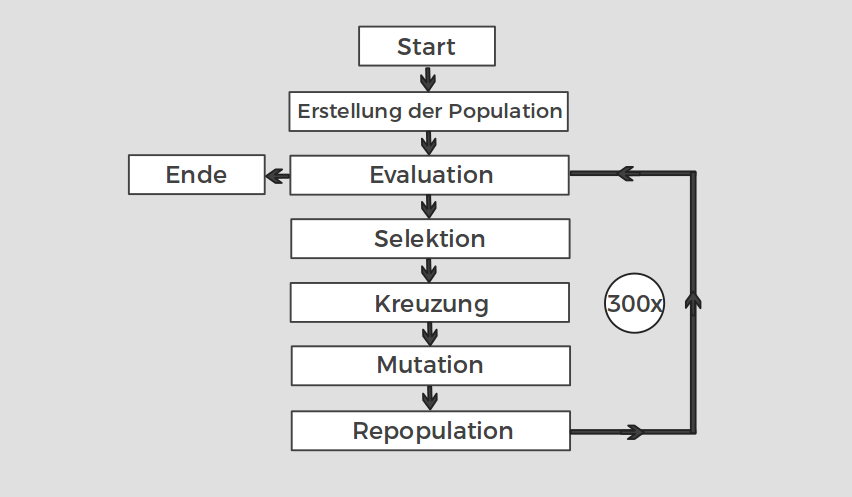
Untersuchung von neuroevolutionären Algorithmen in einer Domäne mit seltener Fitnessfunktion ohne Gradienten

15

Alexander Isenko

19.01.2017

Kompression - Diskrete Kosinus Transformation

1:1

1:5

1:55

Untersuchung von neuroevolutionären Algorithmen in einer Domäne mit seltener Fitnessfunktion ohne Gradienten

16

Alexander Isenko

19.01.2017

Technik #1 - Naive Neuroevolution

Untersuchung von neuroevolutionären Algorithmen in einer Domäne mit seltener Fitnessfunktion ohne Gradienten

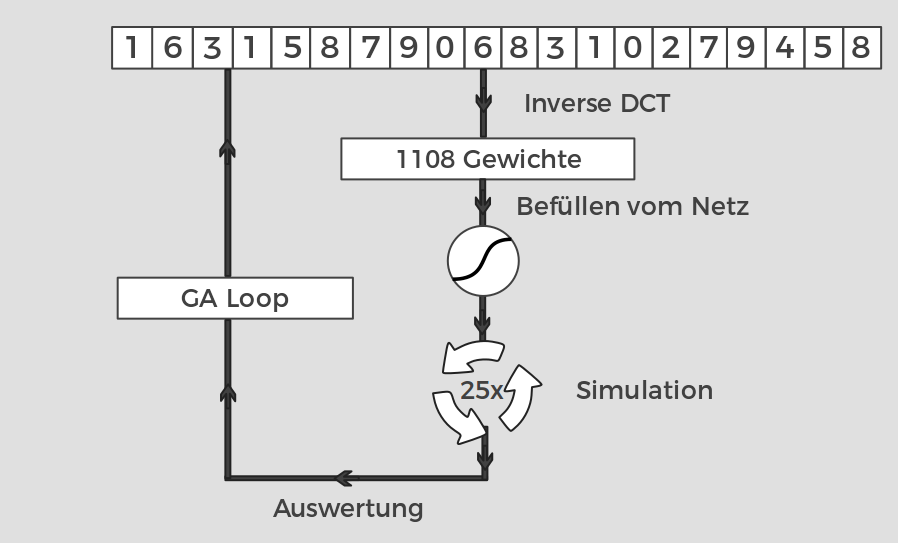
17

Alexander Isenko

19.01.2017

Technik #2 - Cross Entropy Method [5]

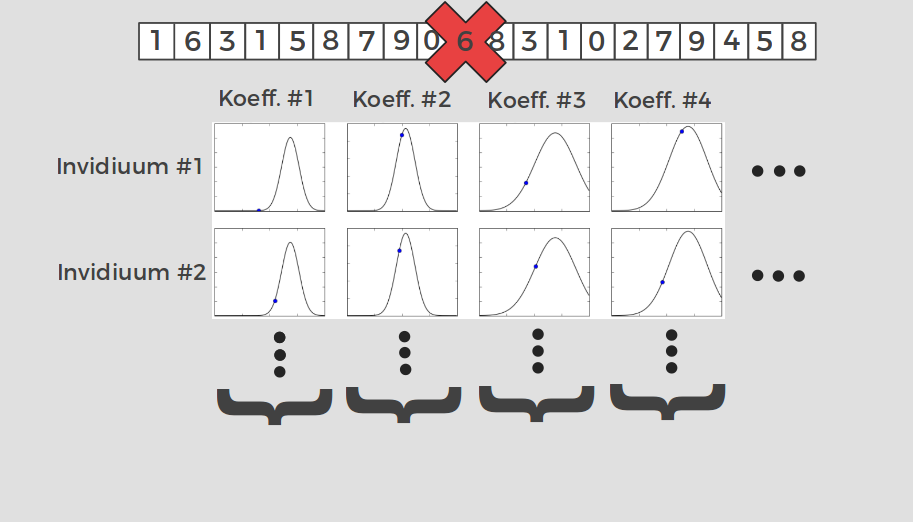
Untersuchung von neuroevolutionären Algorithmen in einer Domäne mit seltener Fitnessfunktion ohne Gradienten

\mu = 3.76

\mu = 3.76

\sigma^2 = 1.58

\sigma^2 = 1.58

\mu = 0.68

\mu = 0.68

\sigma^2 = 1.69

\sigma^2 = 1.69

\mu = 3.81

\mu = 3.81

\sigma^2 = 3.73

\sigma^2 = 3.73

\mu = 3.90

\mu = 3.90

\sigma^2 = 3.44

\sigma^2 = 3.44

\mathcal{N}(x |

\mathcal{N}(x |

)

)

18

Alexander Isenko

19.01.2017

Technik #3 - CoSyNE [4]

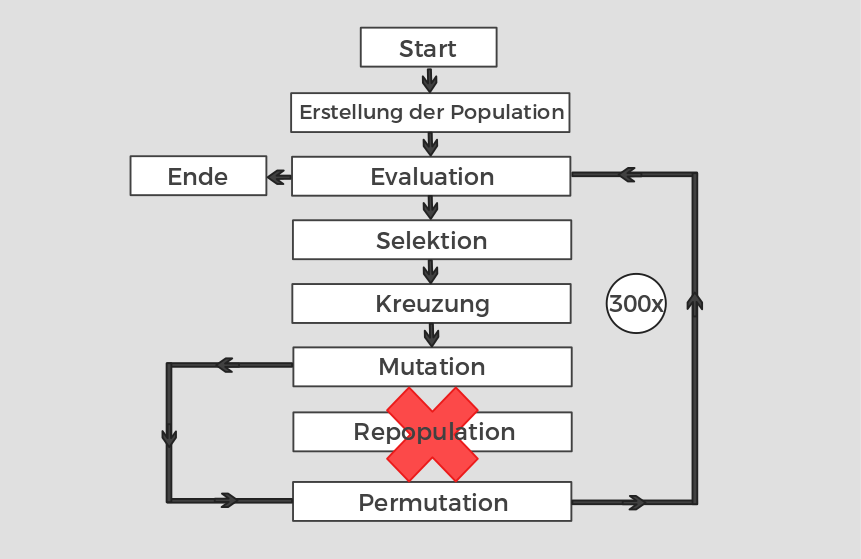
Untersuchung von neuroevolutionären Algorithmen in einer Domäne mit seltener Fitnessfunktion ohne Gradienten

19

Alexander Isenko

19.01.2017

Resultate - Cross Entropy Method

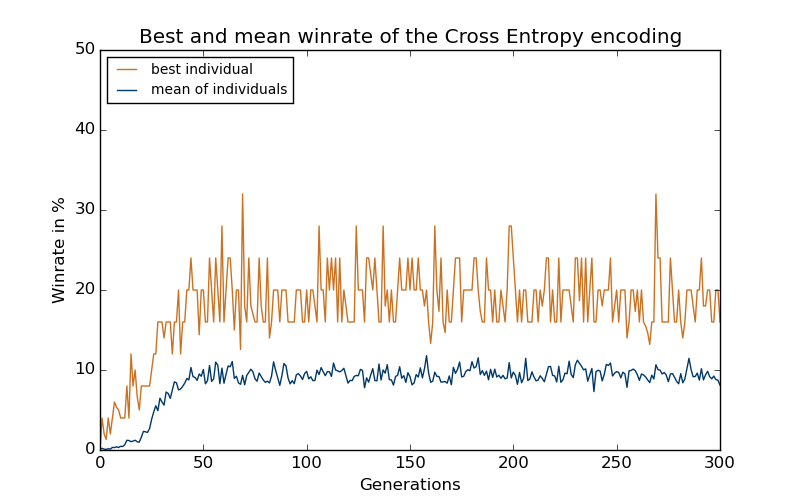
Untersuchung von neuroevolutionären Algorithmen in einer Domäne mit seltener Fitnessfunktion ohne Gradienten

20

Alexander Isenko

19.01.2017

Resultate - Naive Neuroevulution

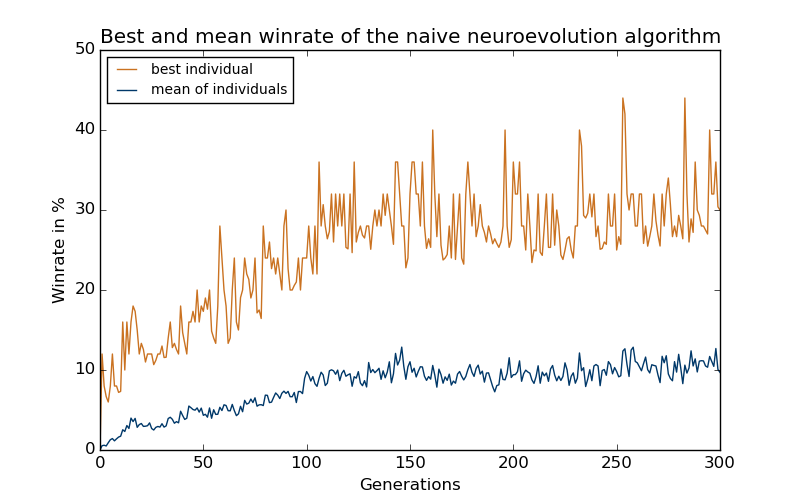
Untersuchung von neuroevolutionären Algorithmen in einer Domäne mit seltener Fitnessfunktion ohne Gradienten

21

Alexander Isenko

19.01.2017

Resultate - CoSyNE

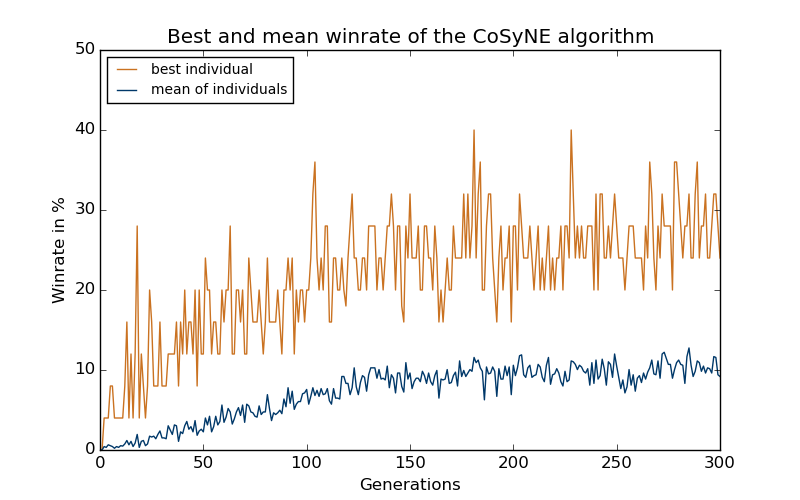
Untersuchung von neuroevolutionären Algorithmen in einer Domäne mit seltener Fitnessfunktion ohne Gradienten

22

Alexander Isenko

19.01.2017

Resultate - Zusammenfassung

Algorithmus	E(Trainierte Fit.)	E(Getestete Fit.)	E(Fehler)
Cross Entropy	29.60%	6.56%	77.87%
CoSyNE	37.60%	12.45%	66.98%
Naive Neuroevo.	42.00%	20.13%	51.93%

Untersuchung von neuroevolutionären Algorithmen in einer Domäne mit seltener Fitnessfunktion ohne Gradienten

23

Alexander Isenko

19.01.2017

Resultate

Video

24

Alexander Isenko

19.01.2017

Ausblick

Die Implementierung und Algorithmus sind erweiterbar auf 4 vs 4 modelliert
OpenAI Gym Aufgabe wurde freigeschaltet ohne bisherige Submissions
Tests gegen Policy Gradient Methoden
CoSyNE + DCT haben bei den Papern viel besser abgeschnitten [4], verschiedene Parametrisierung sollten ausprobiert werden

25

Alexander Isenko

19.01.2017

Referenzen

[1] http://www.robocup.org/leagues

[2] http://www.robocup.org/a_brief_history_of_robocup

[3] https://github.com/LARG/HFO/blob/master/doc/manual.pdf

[4] F. Gomez, J. Schmidhuber, and R. Miikkulainen, “Efficient non-linear control
through neuroevolution,” in Proceedings of the European Conference on Machine
Learning, (Berlin), pp. 654–662, Springer, 2006

[5] https://gym.openai.com/docs/rl

26

Alexander Isenko

19.01.2017

Half Field Offense - Zustandsraum

Winkelkodierung

\text{Sei } f : [0,\pi] \rightarrow [-1, 1] \text{ die Kodierungsfunktion}

\text{Sei } f : [0,\pi] \rightarrow [-1, 1] \text{ die Kodierungsfunktion}

\text{und } g : [-1, 1] \rightarrow [0, \pi] \text{ die inverse Dekodierungsfunktion}:

\text{und } g : [-1, 1] \rightarrow [0, \pi] \text{ die inverse Dekodierungsfunktion}:

f(x) = (\frac{x}{\pi} - 1) \cdot 2, \;\; g(x) = (\frac{x}{2} + 1) \cdot \pi

f(x) = (\frac{x}{\pi} - 1) \cdot 2, \;\; g(x) = (\frac{x}{2} + 1) \cdot \pi

Lagekodierung

max_L = \sqrt{l^2 + b^2} \;\;\;\;\; l,b := \text{L}\ddot{a}\text{nge und Breite des Spielfelds}

max_L = \sqrt{l^2 + b^2} \;\;\;\;\; l,b := \text{L}\ddot{a}\text{nge und Breite des Spielfelds}

\text{Sei } f : [-max_{\text{L}}, max_{\text{L}}] \rightarrow [-1, +1] \text{ die Kodierungsfunktion}

\text{Sei } f : [-max_{\text{L}}, max_{\text{L}}] \rightarrow [-1, +1] \text{ die Kodierungsfunktion}

\text{und } g : [-1, +1] \rightarrow [-max_{\text{L}}, max_{\text{L}}] \text{ die inverse Dekodierungsfunktion} :

\text{und } g : [-1, +1] \rightarrow [-max_{\text{L}}, max_{\text{L}}] \text{ die inverse Dekodierungsfunktion} :

f(x) = \frac{x}{max_{\text{L}}}, \;\; g(x) = x \cdot max_{\text{L}}

f(x) = \frac{x}{max_{\text{L}}}, \;\; g(x) = x \cdot max_{\text{L}}

Boole'sche Kodierung

-1 \;\;\; \text{entspricht} \;\;\; false

-1 \;\;\; \text{entspricht} \;\;\; false

1 \;\;\; \text{entspricht} \;\;\; true

1 \;\;\; \text{entspricht} \;\;\; true

27

Alexander Isenko

19.01.2017

GA - Kodierungsdetails

Generationen	300
Populationsgröße	50
Teamepisoden	25
Episodenzeit	500s
Ball nicht berührt	50s
Selektion	25%
Mutation	10%

28

Alexander Isenko

19.01.2017

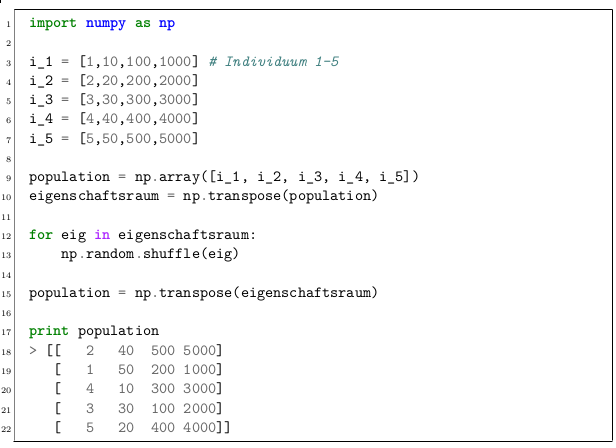
CoSyNE - Beispiel

29

Alexander Isenko

19.01.2017

Fehlerberechung

\text{Fehler} = \frac{F_{\text{Training}} - F_{\text{Test}}}{F_{\text{Training}}}

\text{Fehler} = \frac{F_{\text{Training}} - F_{\text{Test}}}{F_{\text{Training}}}