A programming paradigm that treats computation as the evaluation of mathematical functions and avoids changing-state and mutable data.

Functional Programming

as defined by wikipedia

The borrowing of functional programming concepts into multiparadigm programming languages.

Functional Style

For a given set of inputs (x), a function always returns the same output (y).

f(x) => y

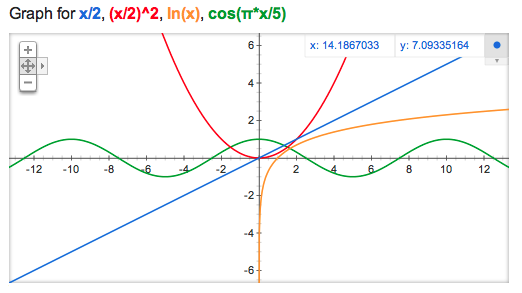
Functions

Not Functions

An arguably useful history of functional programming

Mathematical Functions

Ancient Greece - 17th century

In mathematics, a function is a relation between a set of inputs and a set of permissible outputs with the property that each input is related to exactly one output.

f(x) => y

For a given set of inputs (x), a function (f) always returns the same output (y).

Lambda Calulus

1936

Created by Alonzo Church in 1936,

it is a formal system for expressing computation based on function abstraction and application.

f·g·x

(the application of `x` to the function `g` the result of which is applied to the function `f`)

"Functional" Programming Languages

1950's - Present

Lisp

Scheme

Scala

Clojure

OCaml

Haskell

F#

XQuery

SQL

JavaScript

Ruby

Java8

Python

Perl

C#

Imperative Functional Concepts

see what i did there? 

  • First class functions
  • Higher order functions
  • Pure functions
  • Referential transparency
  • Recursion
let add1 = (x) => x + 1;

(fn) => fn();

(dis, dat) => dis(dat);

let x = add1(1) = 2;

function fn(x) { x ? fn(x-1) : x }

Non-Functional ≠ Non-Functioning

OOP

OOP combines data (properties) and associated behavior (methods) into a single location (an “object”).

Functional

FP moves data through  functions which produce the effect of behavior.

class Pizza {
  constructor(toppings=[]) {
    this.toppings = toppings; //data
  }

  addToppings(toppings) { //behavior
    for (topping of toppings) {
        this.toppings.push(topping);
    }
  }
}
const pizza = { //data
    toppings: []
};

//behavior
const addToppings = (toppings, dish) => ({
    ...dish,
    toppings: [...dish.toppings, ...toppings]
});

OOP

OOP tends to be imperative -- describing how --, more domain specific and stateful

Functional

FP tends to be declarative in nature -- describing what --, more abstract and stateless.

class Pizza {
  constructor(toppings=[]) {
    this.toppings = toppings;
  }

  addToppings(toppings) {
    for (topping of toppings) {
        this.toppings.push(topping);
    }
  }
}

const pizza = new Pizza();
pizza.addToppings(['pepperoni'])
const pizza = {
    toppings: []
};

const addToppings = (toppings, dish) => ({
    ...dish,
    toppings: [...dish.toppings, ...toppings]
});

addToppings(['pepperoni'], pizza);

OOP

OOP views applications as collection of object models and how they relate to each other.

Functional

FP views applications as an orchestration of data transformations.

Food 
    -Desert
        - Pie
            - Pizza
 
pizza -> 
    makeDough -> 
    applySause -> 
    addToppings -> 
    bake

Paradigm shifts

Functional programming is a paradigm shift from OOP. As with any paradigm shift, if one attempts to bring preconceptions from a previous paradigm, one's experience in the new paradigm will be less than satisfactory. 

 

When starting out in a new paradigm, be prepared to challenge preconceptions. Have an open mind and try to go with the grain of the paradigm as much as possible. 

The reason functional programming forces you to learn so much is because it challenges every assumption about writing software that you had.

Vasily Vasinov - 16 Months of Functional Programming

You won't get it, until you do.

My experience with functional style programming is that it won't make a whole lot of sense until you force yourself to fully embrace it.

 

When starting, expect to take several times longer to accomplish your goal that it would have otherwise. 

 

How long did it take you to iterate through a list on day one. All the little micro patterns and practices you have built over the years you hadn't obtained yet. Don't expect shortcuts.

That's it‽
It feels so anti-climatic!

Expect that the amount of code you produce to be disproportionately small compared to the amount of time you spend on it. This can initially feel like you are not being productive. Functional code tends to be terse, yet expressive. There also tends to be fewer bugs in the code that need to be addressed after.

First Order Functions?

First Class Functions/Higher Order Functions

First Class Functions

In functional style programming, functions are first class citizens, meaning functions can be used the same as any other reference. They can be assigned to variables, they can be passed as arguments or they can be returned as values from other functions.

Higher Order Functions

The concept of higher order functions is closely related to the functions as first class citizens.

 

A function is a higher order function if:

  1. It accepts a function as an argument.

    or
     
  2. It returns a function as a result.

Higher Order Functions

Higher order functions form the foundations of functional style programming.

 

They can be used to "customize" a generic function.

const isNamed = (name) => 
    (item) => item.name === name;
const isNamedCory = isNamed('Cory');

higher order function because...

it returns a function

Higher Order Functions

They can abstract a pattern of processing.

const filter = (how, what) =>
    let filtered = [];
    for (item of what) {
        filtered = how(item) 
            ? [...filtered, item] 
            : filtered;
    }
    return filtered;

 

filter(isNamedCory, ['Cory', 'Jared', 'Matt']);

higher order because it accepts a function.

Higher Order Functions

They can compose other functions together.

const compose = (...fns) => 
  (val) => 
    fns.reduce(
      (v, f) => f(v), 
      val
    );
const app = compose(fn1, fn2, fn3);

app(initialState);

higher order because it accepts and returns functions

Yeah, but what've you done for me lately?

classical vs functional examples.

Think of the children

classical

Think of the children

Functional

Hey Siri...

show me...

  1. Movies
  2. Made in the last 20 years
  3. Staring Morgan Freeman
  4. That are kid friendly
  5. and educational

do it

Hey Siri...

show me...

  1. Movies
  2. Made in the last 20 years
  3. Staring Morgan Freeman
  4. That are kid friendly
  5. and educational

impare me

Regrouping

Let's group our movies by genre

Thinking Functionally

Think about the problem set, rather than the problem itself.

What are you doing to the data?

Have you done similar things in other scenarios?

How can those similar problems be universally described with functions?

Thinking Functionally

Another way to think functionally is to start with your whole problem set as one unit. Then subdivide that unit into discrete smaller units at the same abstraction level.

Keep doing this until you have atomic functions. Functions that cannot be broken into more discrete pieces of functionality.

You have just deconstructed a functional solution. :)