Soss: Lightweight Probabilistic Programming in Julia

Chad Scherrer

Senior Data Scientist, Metis

GLOBAL BIG DATA

CONFERENCE

About Me

Served as Technical Lead for language evaluation for the DARPA program
Probabilistic Programming for Advancing Machine Learning (PPAML)

PPL Publications

Scherrer, Diatchki, Erkök, & Sottile, Passage : A Parallel Sampler Generator for Hierarchical Bayesian Modeling, NIPS 2012 Workshop on Probabilistic Programming
Scherrer, An Exponential Family Basis for Probabilistic Programming, POPL 2017 Workshop on Probabilistic Programming Semantics
Westbrook, Scherrer, Collins, and Mertens, GraPPa: Spanning the Expressivity vs. Efficiency Continuum, POPL 2017 Workshop on Probabilistic Programming Semantics

Making Rational Decisions

Managed Uncertainty

Rational Decisions

Bayesian Analysis

Probabilistic Programming

Physical systems
Hypothesis testing
Modeling as simulation

Medicine
Finance
Insurance

Risk

Custom models

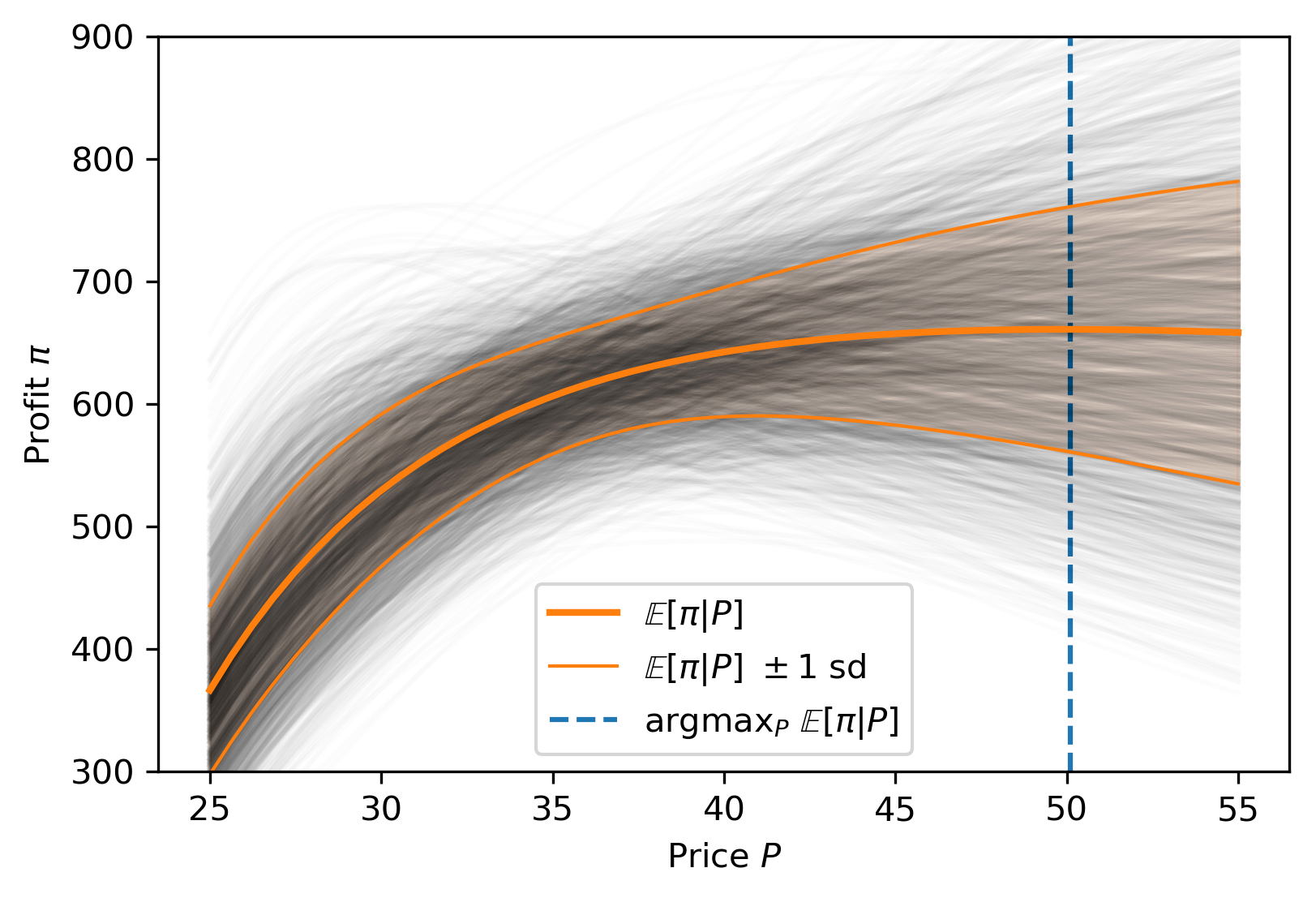
Business Applications

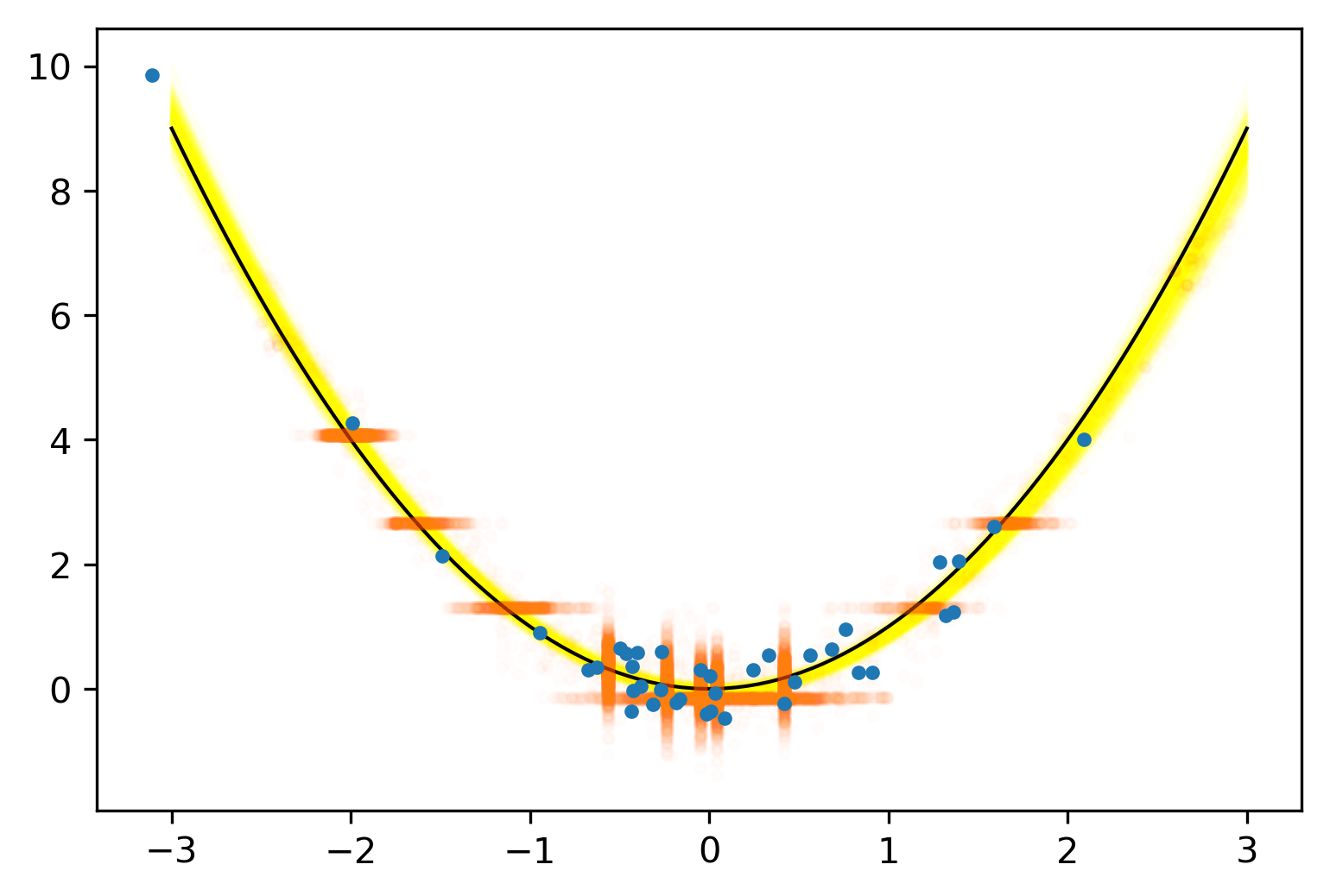
https://cscherrer.github.io/post/max-profit/

Missing Data

The Two-Language Problem

A disconnect between the "user language" and "developer language"

Python

C

Deep Learning Framework

Harder for beginner users
Barrier to entry for developers
Limits extensibility

A New Approach in Julia

Models begin with "Tilde code" based on math notation
A Model is a "lossless" data structure
Combinators transform code before compilation

Model

Tilde code

\begin{aligned} \mu &\sim \text{Normal}(0,5)\\ \sigma &\sim \text{Cauchy}_+(0,3) \\ x_j &\sim \text{Normal}(\mu,\sigma) \end{aligned}

Advantages

Transparent
Composable
Backend-agnostic
No intrinsic overhead

A (Very) Simple Example

P(\mu,\sigma|x)\propto P(\mu,\sigma)P(x|\mu,\sigma)

\begin{aligned} \mu &\sim \text{Normal}(0,5)\\ \sigma &\sim \text{Cauchy}_+(0,3) \\ x_j &\sim \text{Normal}(\mu,\sigma) \end{aligned}

m = @model N begin
    μ ~ Normal(0, 5)
    σ ~ HalfCauchy(3)
    x ~ Normal(μ, σ) |> iid(N)
end

Theory

Soss

julia> sourceLogdensity(m)
:(function ##logdensity#1168(pars)
      @unpack (μ, σ, x, N) = pars
      ℓ = 0.0
      ℓ += logpdf(Normal(0, 5), μ)
      ℓ += logpdf(HalfCauchy(3), σ)
      ℓ += logpdf(Normal(μ, σ) |> iid(N), x)
      return ℓ
  end)

A (Slightly Less) Simple Example

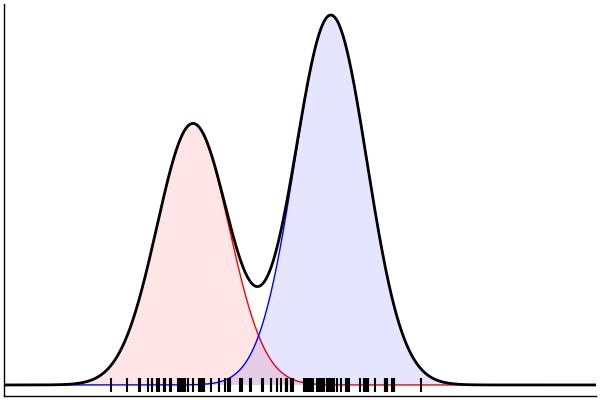
gaussianMixture = @model begin
    N ~ Poisson(100)
    K ~ Poisson(2.5)
    p ~ Dirichlet(K, 1.0)
    μ ~ Normal(0,1.5) |> iid(K)
    σ ~ HalfNormal(1)
    θ = [(m,σ) for m in μ]
    x ~ MixtureModel(Normal, θ, p) |> iid(N)
end

julia> m = gaussianMixture(N=100,K=2)
@model begin
    p ~ Dirichlet(2, 1.0)
    μ ~ Normal(0, 1.5) |> iid(2)
    σ ~ HalfNormal(1)
    θ = [(m,σ) for m in μ]
    x ~ MixtureModel(Normal, θ, p) |> iid(N)
end

Sampling From the Model

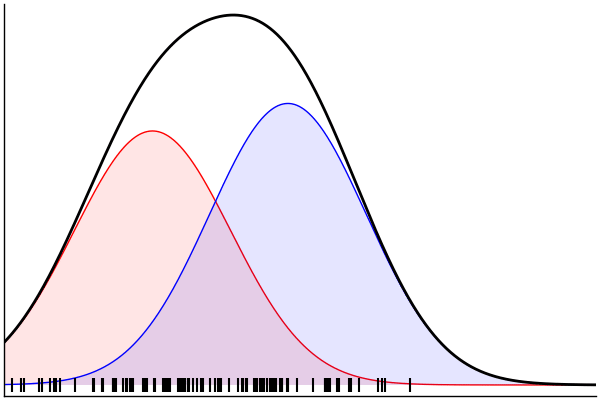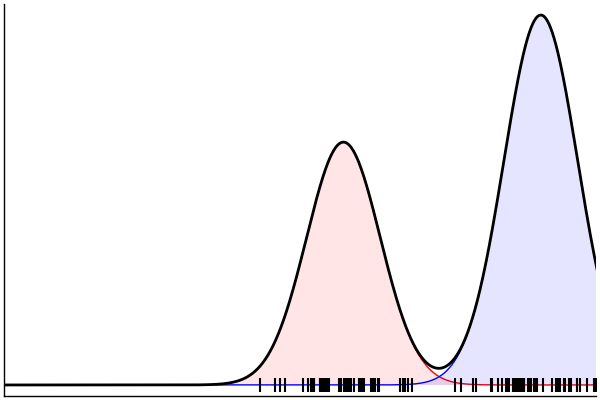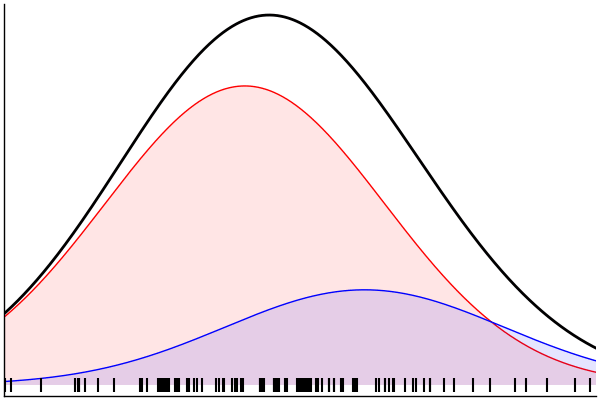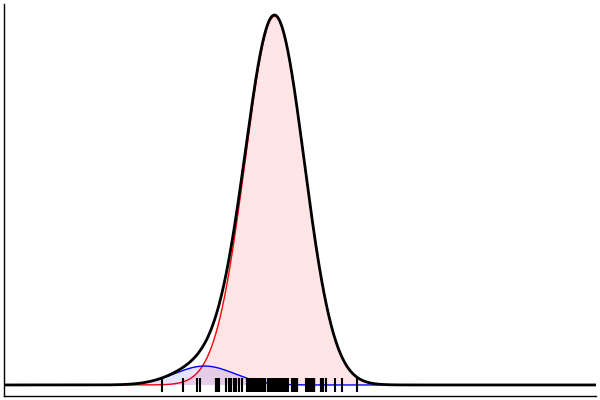
julia> rand(m) |> pairs
pairs(::NamedTuple) with 4 entries:
  :p => 0.9652
  :μ => [-1.20, 3.121]
  :σ => 1.320
  :x => [-1.780, -2.983, -1.629, ...]

(Dynamic) Conditioning: Forward Model

rand(m_fwd; groundTruth...)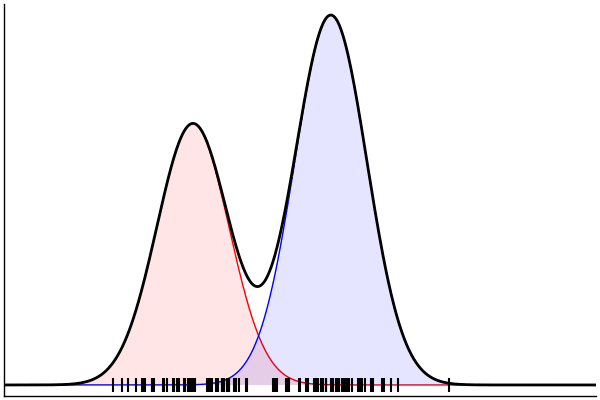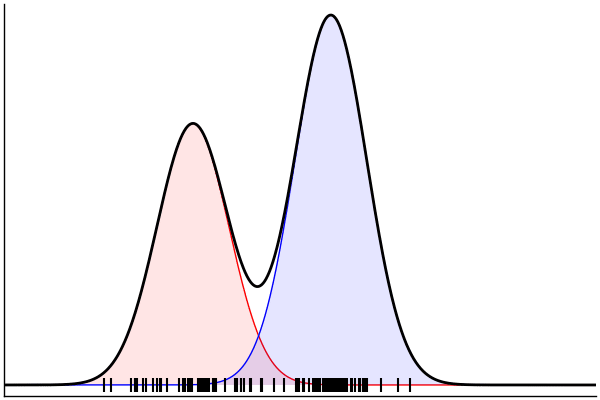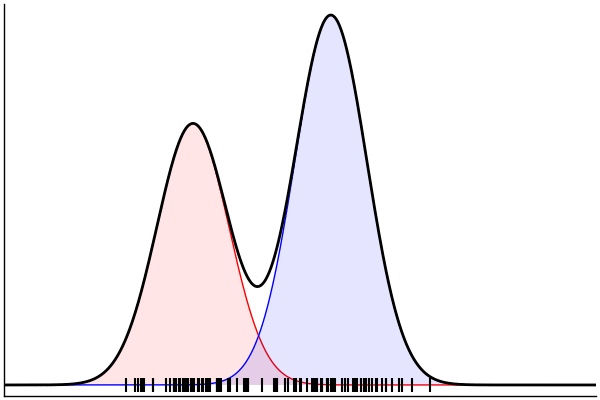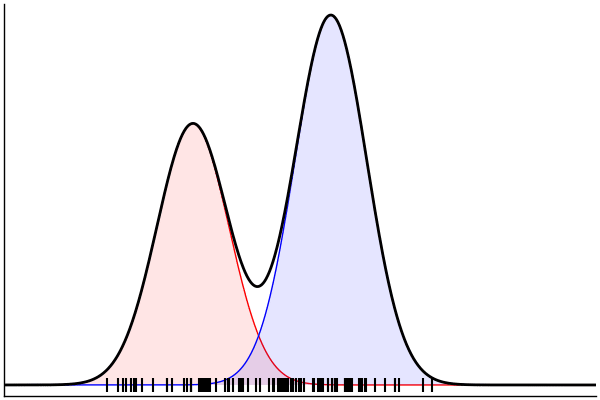

julia> m_fwd = m(:p,:μ,:σ)
@model (p, μ, σ) begin
    θ = [(m, σ) for m = μ]
    x ~ MixtureModel(Normal,θ,[p,1-p]) |> iid(100)
end

m = @model begin
    p ~ Uniform()
    μ ~ Normal(0, 1.5) |> iid(2)
    σ ~ HalfNormal(1)
    θ = [(m, σ) for m in μ]
    x ~ MixtureModel(Normal,θ,[p,1-p]) |> iid(100)
end

(Dynamic) Conditioning: Inverse Model

post = nuts(m_inv; groundTruth...)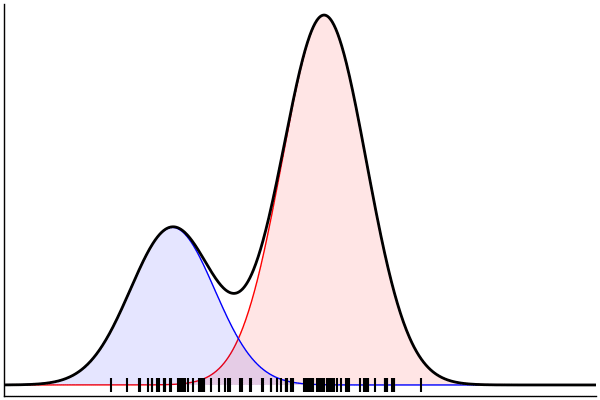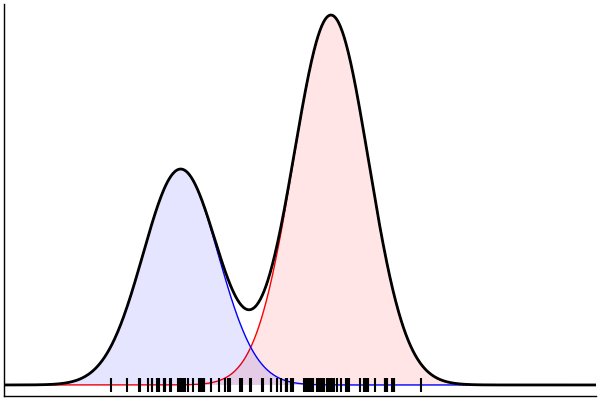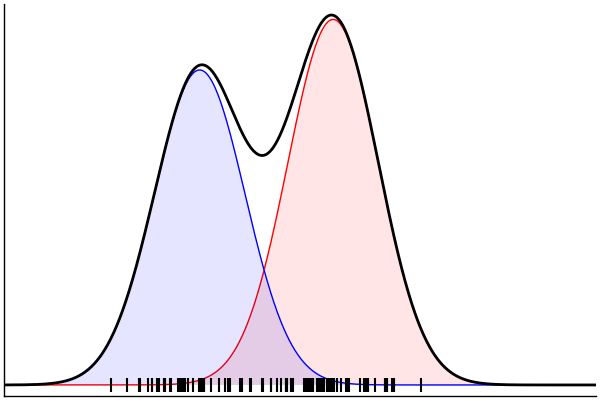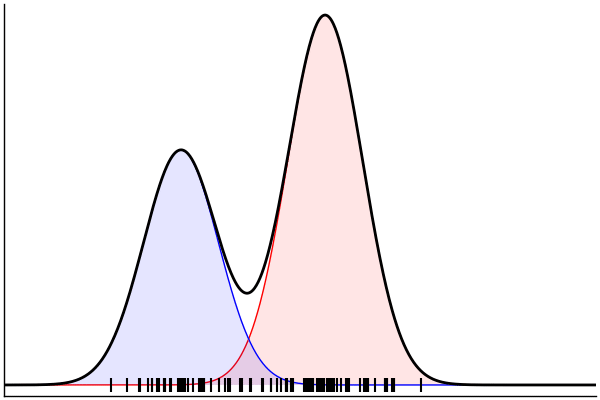

julia> m_inv = m(:x)
@model x begin
    p ~ Uniform()
    μ ~ Normal(0, 1.5) |> iid(2)
    σ ~ HalfNormal(1)
    θ = [(m, σ) for m = μ]
    x ~ MixtureModel(Normal,θ,[p,1-p]) |> iid(100)
end

m = @model begin
    p ~ Uniform()
    μ ~ Normal(0, 1.5) |> iid(2)
    σ ~ HalfNormal(1)
    θ = [(m, σ) for m in μ]
    x ~ MixtureModel(Normal,θ,[p,1-p]) |> iid(100)
end

Posterior Predictive Checks

\theta_1

\theta_2

\theta_n

x^\text{rep}_1

x^\text{rep}_2

\vdots

Static Dependency Analysis

julia> lda
@model (α, η, K, V, N) begin
    M = length(N)
    β ~ Dirichlet(repeat([η],V)) |> iid(K)
    θ ~ Dirichlet(repeat([α],K)) |> iid(M)
    z ~ For(1:M) do m
            Categorical(θ[m]) |> iid(N[m])
        end
    w ~ For(1:M) do m
            For(1:N[m]) do n
                Categorical(β[(z[m])[n]])
            end
        end
end

julia> dependencies(lda)
               [] => :α
               [] => :η
               [] => :K
               [] => :V
               [] => :N
             [:N] => :M
     [:η, :V, :K] => :β
     [:α, :K, :M] => :θ
     [:M, :θ, :N] => :z
 [:M, :N, :β, :z] => :w

Blei, Ng, & Jordan (2003). Latent Dirichlet Allocation. JMLR, 3(4–5), 993–1022.

In the Works

First-class models
Symbolic simplification via SymPy or REDUCE
Constant-space streaming models (particle or Kalman filter)
Reparameterizations ("noncentering", etc)
Deep learning via Flux
Variational inference a la Pyro
Simulation-based modeling via Turing

logo by James Fairbanks, on Julia Discourse site

JuliaCon 2019

July 21-27

Baltimore, MD

Thank You!

https://cscherrer.github.io/

https://github.com/cscherrer/Soss.jl