Computing Bottom SCCs Symbolically Using Transition Guided Reduction

Nikola Beneš, Luboš Brim, Samuel Pastva, and David Šafránek

Labelled transition systems (LTS)

  • A finite set of states (S)
  • A finite set of labels (L)
  • A transition relation for each label:
\forall a \in L \ \xrightarrow{a} \subseteq S \times S

By erasing labels, we get a normal directed graph...

Why labelled transition systems then?

SYMBOLIC COMPUTATION

Sets and relations are represented symbolically.

(We use binary decision diagrams)

\text{Post}(a, X) = \{ s' \in S \mid \exists s \in X. s \xrightarrow{a} s' \}
\text{Pre}(a, X) = \{ s \in S \mid \exists s' \in X. s \xrightarrow{a} s' \}
\text{CanPost}(a, X) = \{ s \in S \mid \exists s' \in X. s \xrightarrow{a} s' \}

With these we can build sets of forward and backward reachable states...

\text{Fwd}(X) \text{ , } \text{Bwd}(X)

* saturation

LTS Operations

BOTTOM STRONGLY CONNECTED COMPONENTS

Goal: Identify the subsets of S that represent the bottom (terminal) strongly connected components (BSCCs).

Useful term: A subset of S is SCC-closed if whenever it contains some state x, it also contains the SCC "around" x.

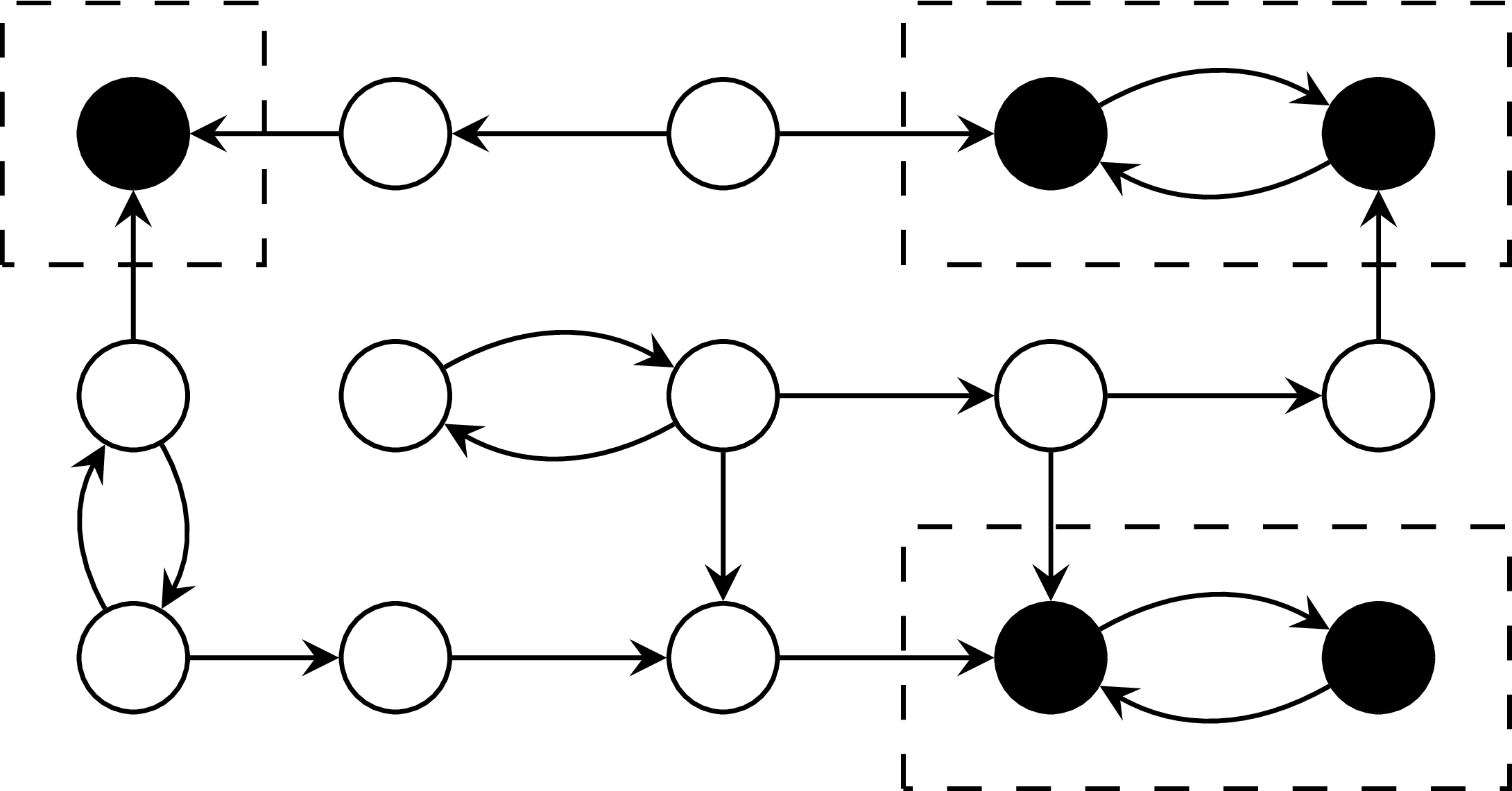
"Basic" BSCC Algorithm

while S != empty:
  ​pivot = PICK(S);
  B = BWD(pivot);
  F = FWD(pivot);
  if F is subset of B:
    report F as BSCC;   
  S = S \ B;
Graph
Pivot Vertex ⇒

"Basic" BSCC Algorithm

Graph
Pivot Vertex ⇒ 
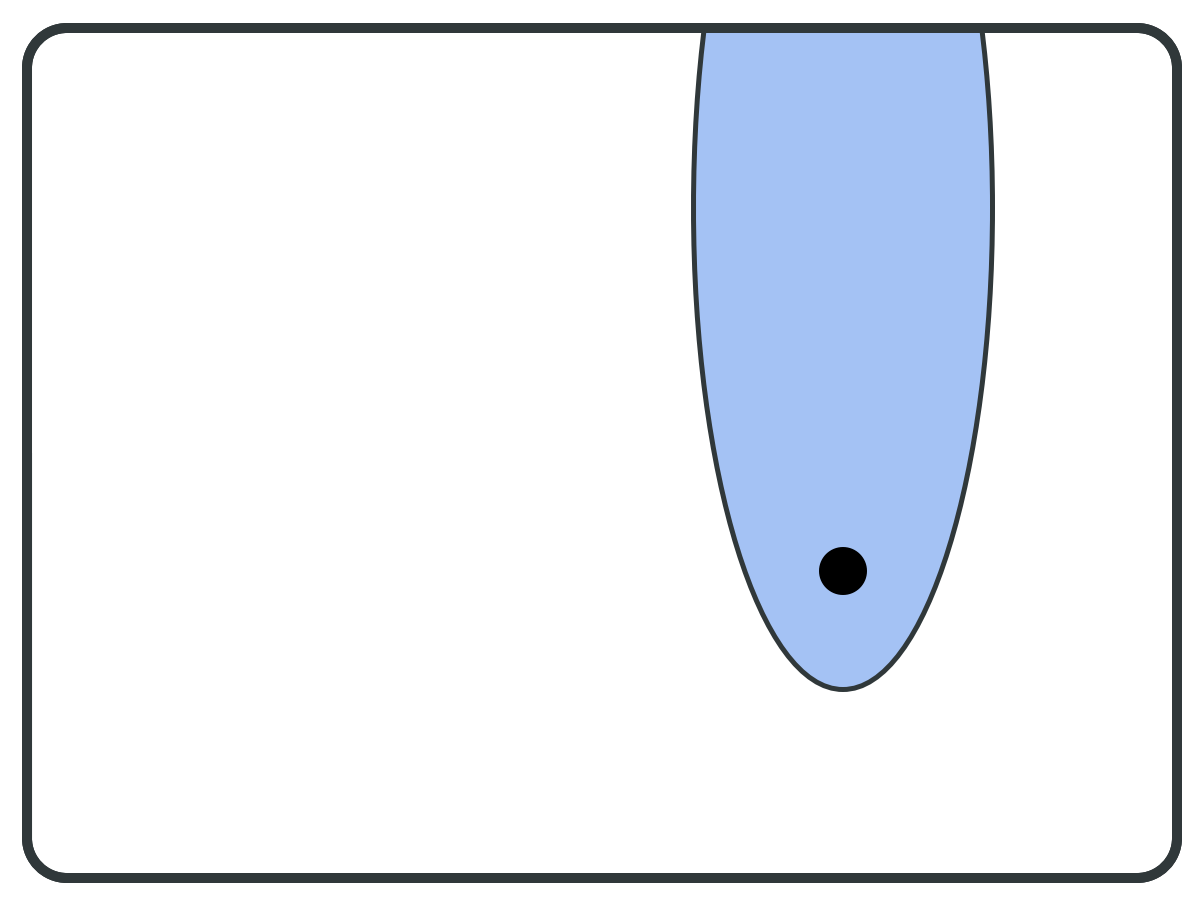
Backward 
set (B) ⇒ 
while S != empty:
  ​pivot = PICK(S);
  B = BWD(pivot);
  F = FWD(pivot);
  if F is subset of B:
    report F as BSCC;   
  S = S \ B;

"Basic" BSCC Algorithm

Graph
Backward 
set (B) ⇒ 
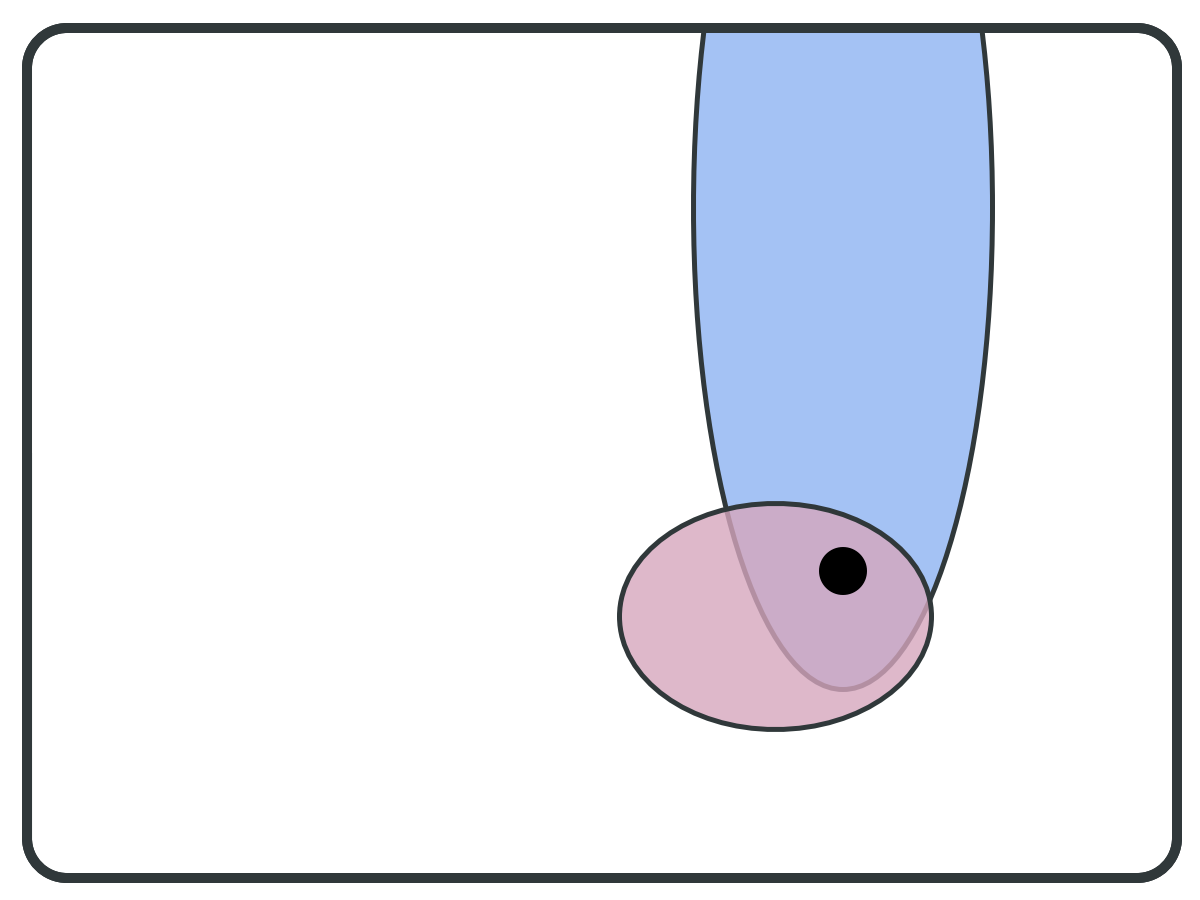
Forward 
set (F) ⇒ 
while S != empty:
  ​pivot = PICK(S);
  B = BWD(pivot);
  F = FWD(pivot);
  if F is subset of B:
    report F as BSCC;   
  S = S \ B;

"Basic" BSCC Algorithm

Graph
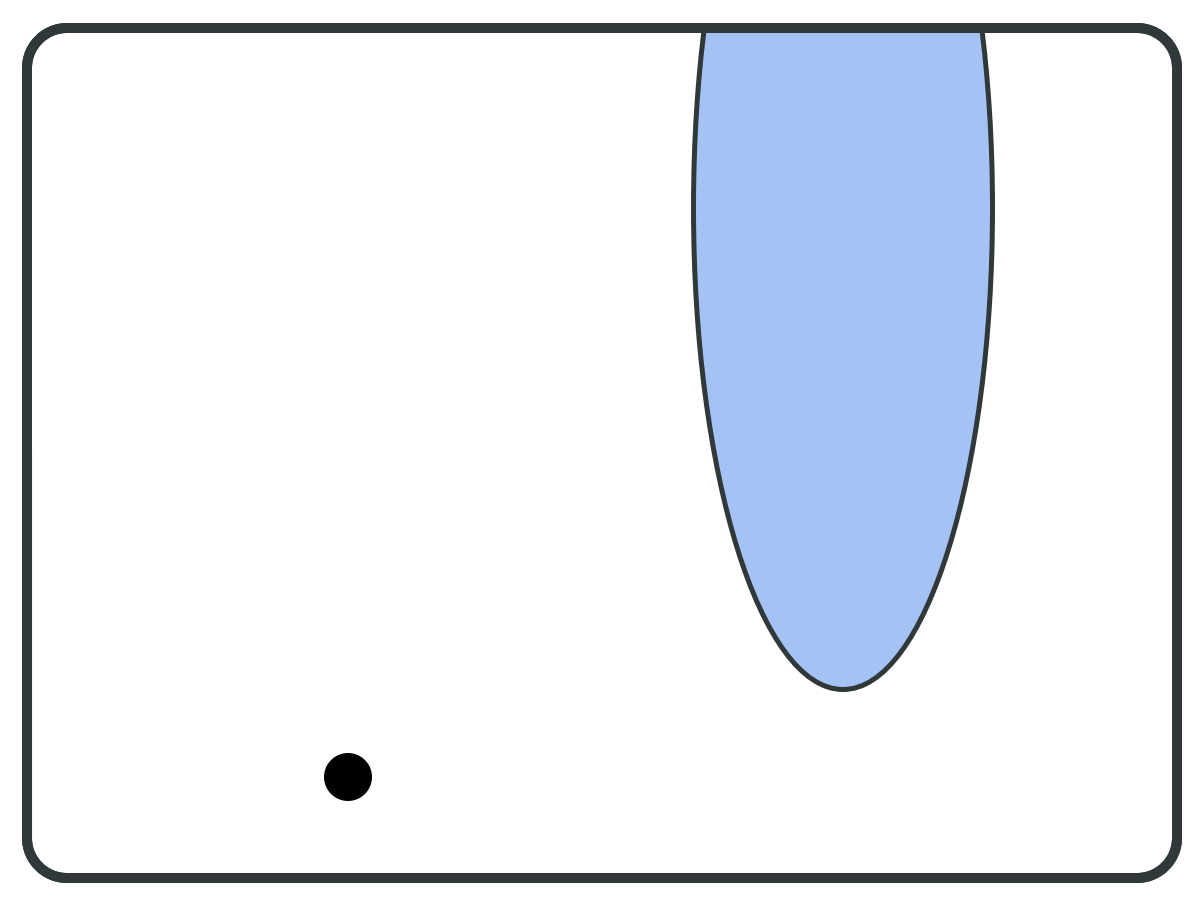
⇐ Pivot Vertex

×

Useful "tricks":

  • Stop computation of F as soon as it leaves B.
  • Pick pivot from F \ B when possible (instead of random)...

SCC-closed!

while S != empty:
  ​pivot = PICK(S);
  B = BWD(pivot);
  F = FWD(pivot);
  if F is subset of B:
    report F as BSCC;   
  S = S \ B;

Works well when BSCC IS large, but AN interesting BSCC RARELY IS!

Graph
10^30
10^10
0.000000000000000001%
⇐

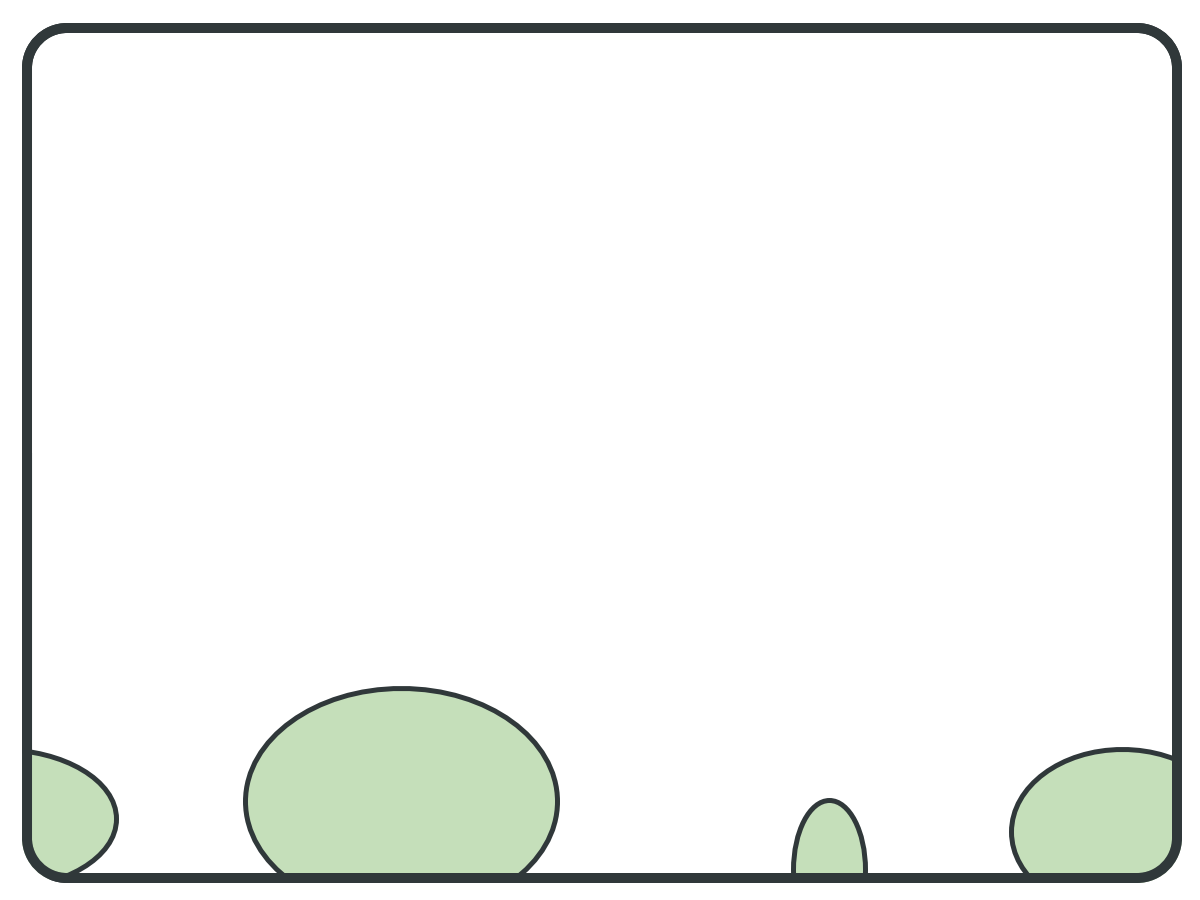
Two ways this can go wrong:

  1. Poor pivot selection
  2. Large graph diameter

×

×

×

×

×

×

×

×

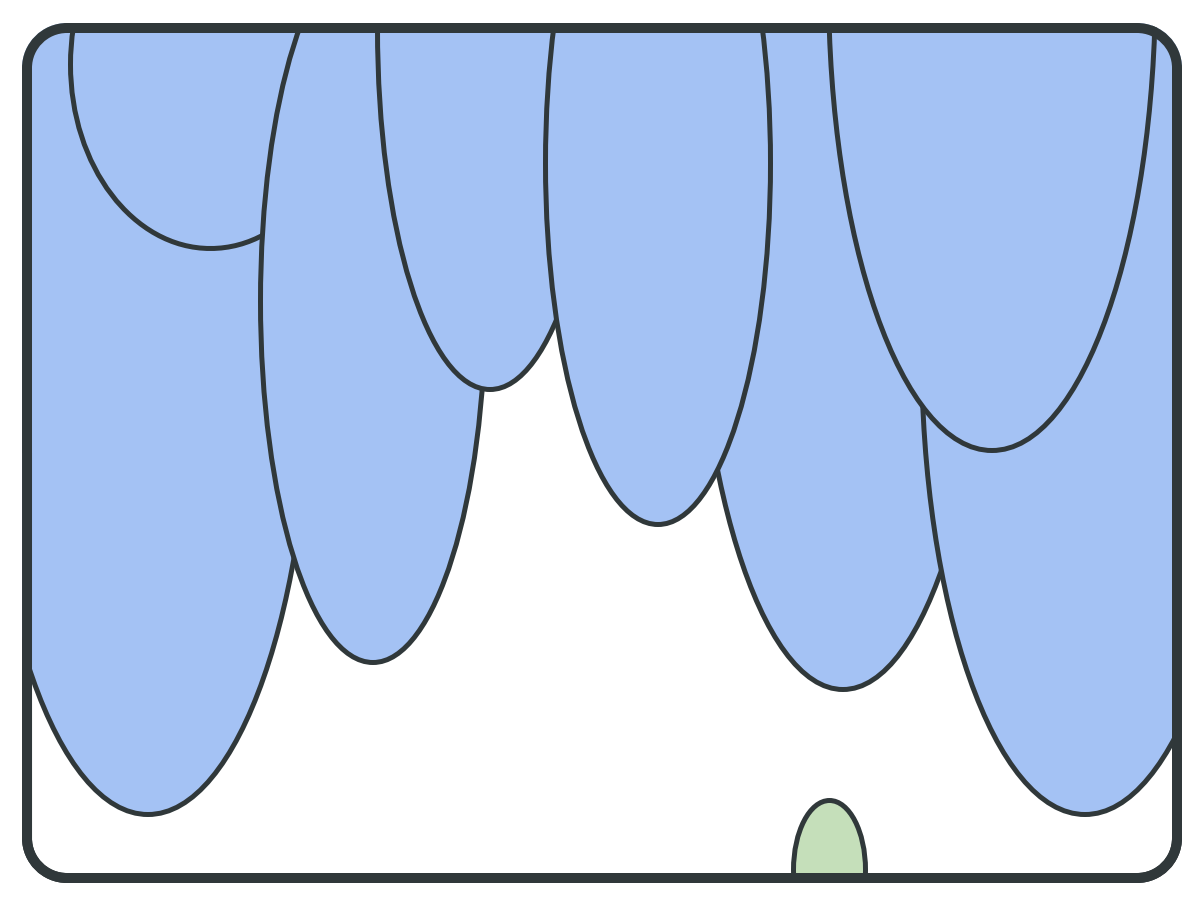
y
x
x << y

Three ways...

Graph

×

​reduce(S, pivots):
  B = BWD(pivots);
  F = FWD(pivots);
​  S = S \ (B \ F);
  bottom = F \ B;
  B' = BWD(bottom);
  S = S \ (B' \ bottom);
  return S;
​

REDUCTION PRINCIPLE

⇐ Pivot  Set
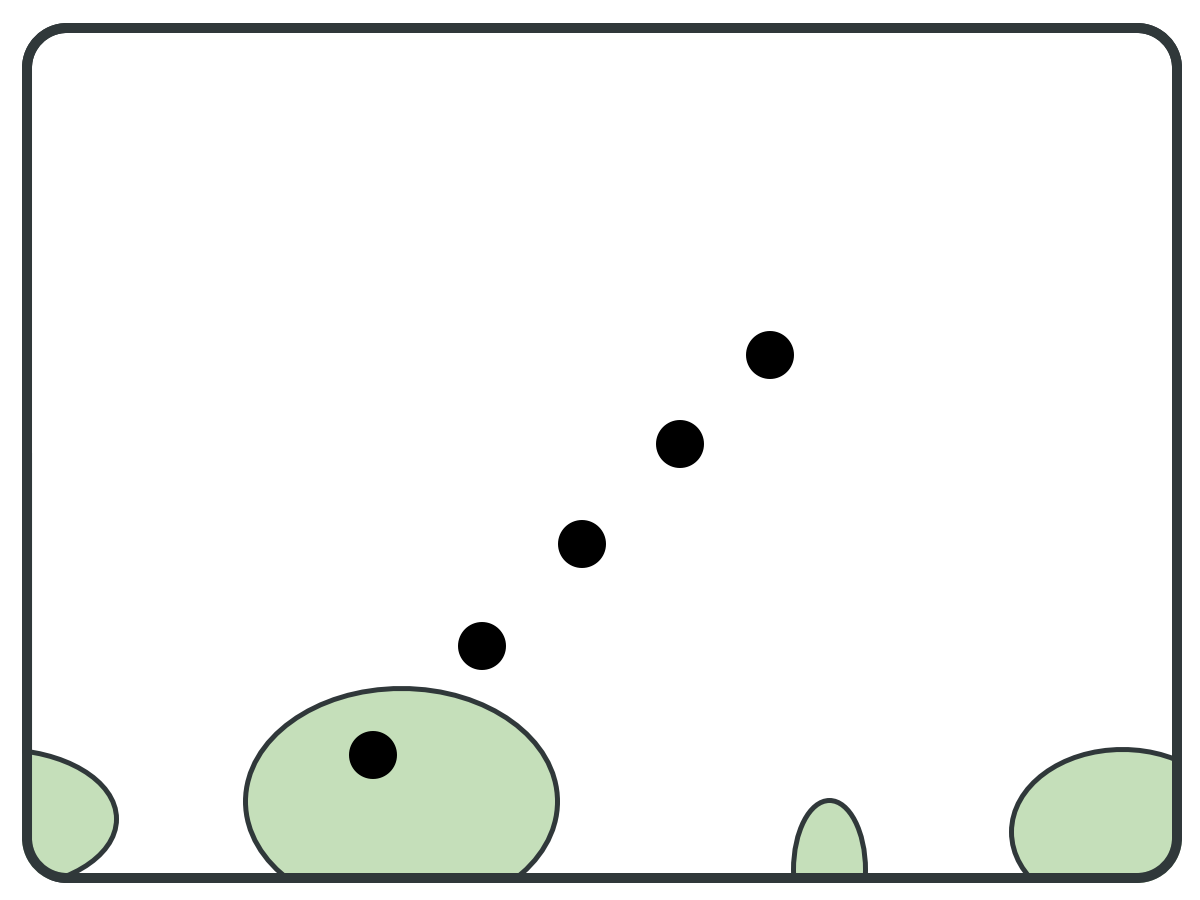
​reduce(S, pivots):
  B = BWD(pivots);
  F = FWD(pivots);
​  S = S \ (B \ F);
  bottom = F \ B;
  B' = BWD(bottom);
  S = S \ (B' \ bottom);
  return S;
​

REDUCTION PRINCIPLE

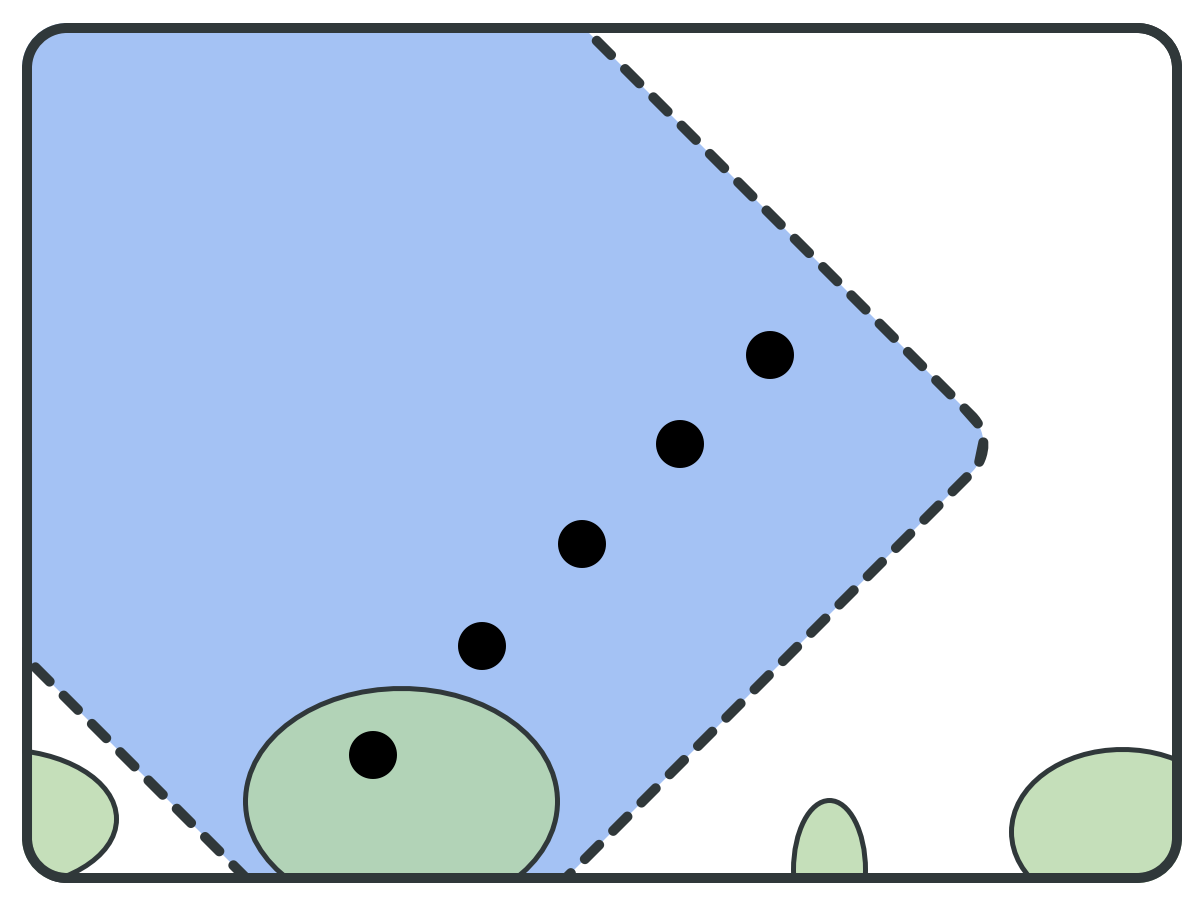
Backward set (B) 
​reduce(S, pivots):
  B = BWD(pivots);
  F = FWD(pivots);
​  S = S \ (B \ F);
  bottom = F \ B;
  B' = BWD(bottom);
  S = S \ (B' \ bottom);
  return S;
​

REDUCTION PRINCIPLE

Backward set (B) 
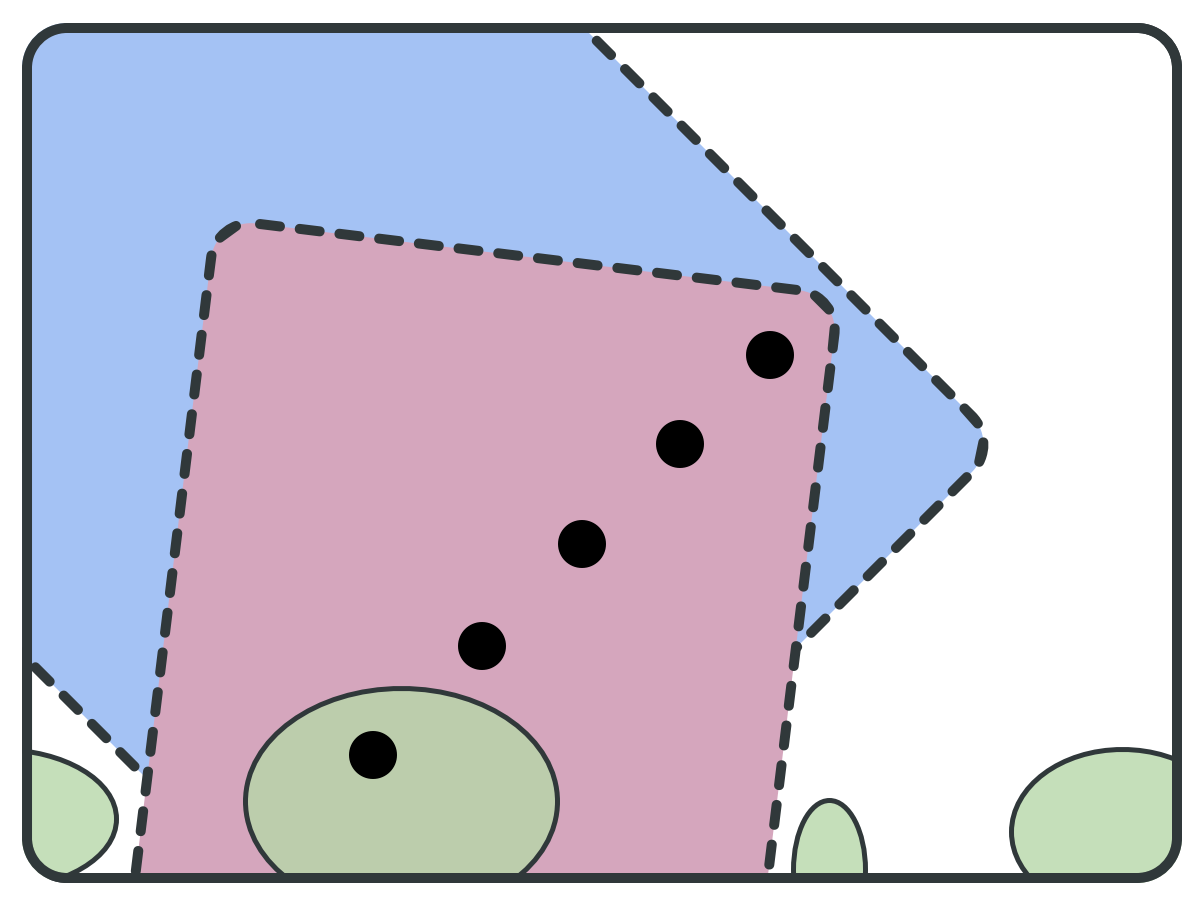
Forward Set 
(F) 
​reduce(S, pivots):
  B = BWD(pivots);
  F = FWD(pivots);
​  S = S \ (B \ F);
  bottom = F \ B;
  B' = BWD(bottom);
  S = S \ (B' \ bottom);
  return S;
​

REDUCTION PRINCIPLE

Backward set (B) 
Forward Set 
(F)

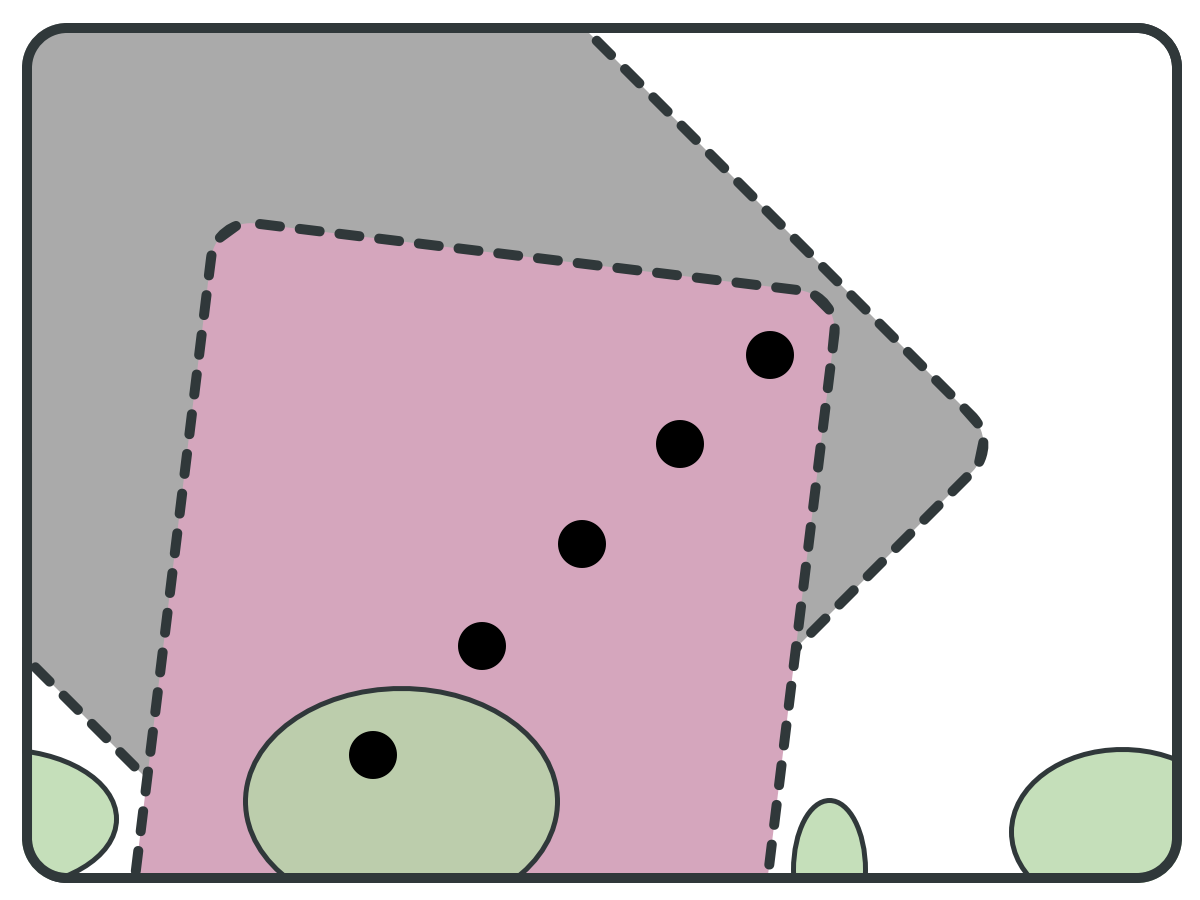
Because F is

SCC-closed

​reduce(S, pivots):
  B = BWD(pivots);
  F = FWD(pivots);
​  S = S \ (B \ F);
  bottom = F \ B;
  B' = BWD(bottom);
  S = S \ (B' \ bottom);
  return S;
​

REDUCTION PRINCIPLE

Backward set (B) 
Forward Set 
(F)

F \ B is also

SCC-closed

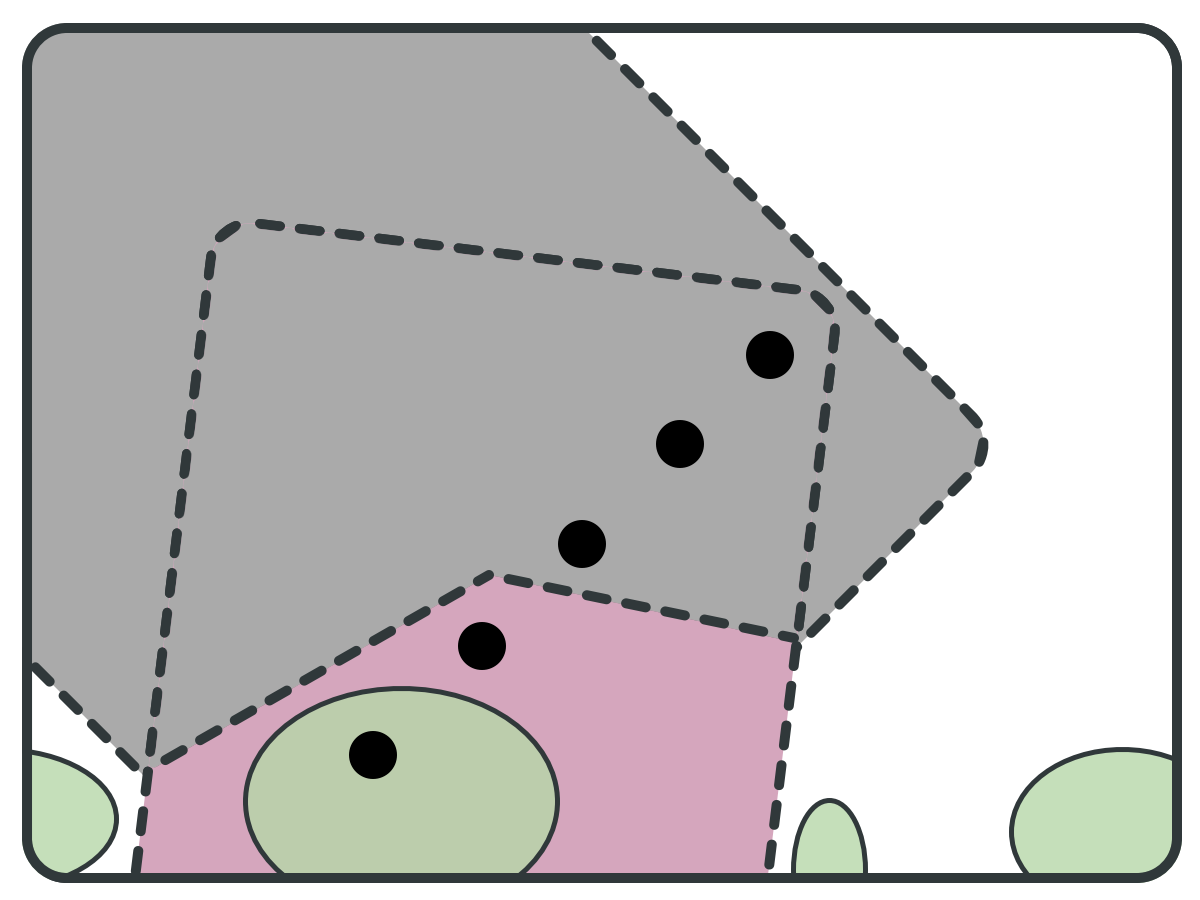
Who picks the pivots?

for every a in L:
  S = reduce(S, CanPost(a, S));

(T)ransition (G)uided (R)eduction

But why does it work?

All BSCCs rarely use all transition labels. Using TGR, we prune the graph based on which transitions can be actually used infinitely often in the reachable state space.

Are we done yet?

a) TGR eliminates almost all non-BSCC states. ✓

b) Performance depends on the ordering of labels.

A lot.

Interleaving?

Start reducing a.
Remove 10.000 states.
Start reducing b.
Remove 10^20 states.

...

Interleaving!

Start reducing a.
Start reducing b.
Start reducing c.
Start reducing d.
Nothing
10^20 states
5.000 states
10^6 states

The process with the smallest symbolic representation advances in every step.

  1. Reductions that can be computed quickly finish first.
  2. Completed reductions speed up the remaining processes (less remaining state space).

(I)nterleaved (T)ransition (G)uided (R)eduction

Experiments and Evaluation

125 real models, up to 2^350 states
ITGR vs. CABEAN

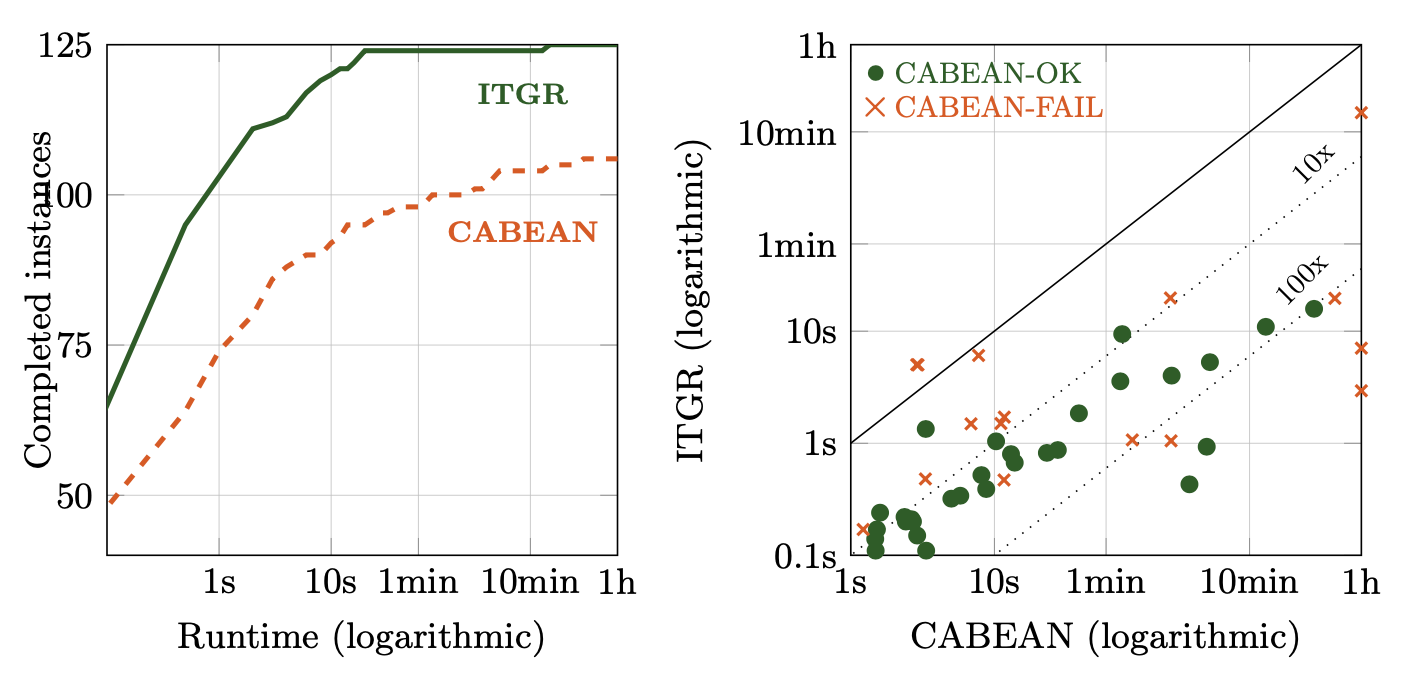
Experiments and Evaluation

125 real + 100 random, up to 2^1000 states
ITGR vs. TGR
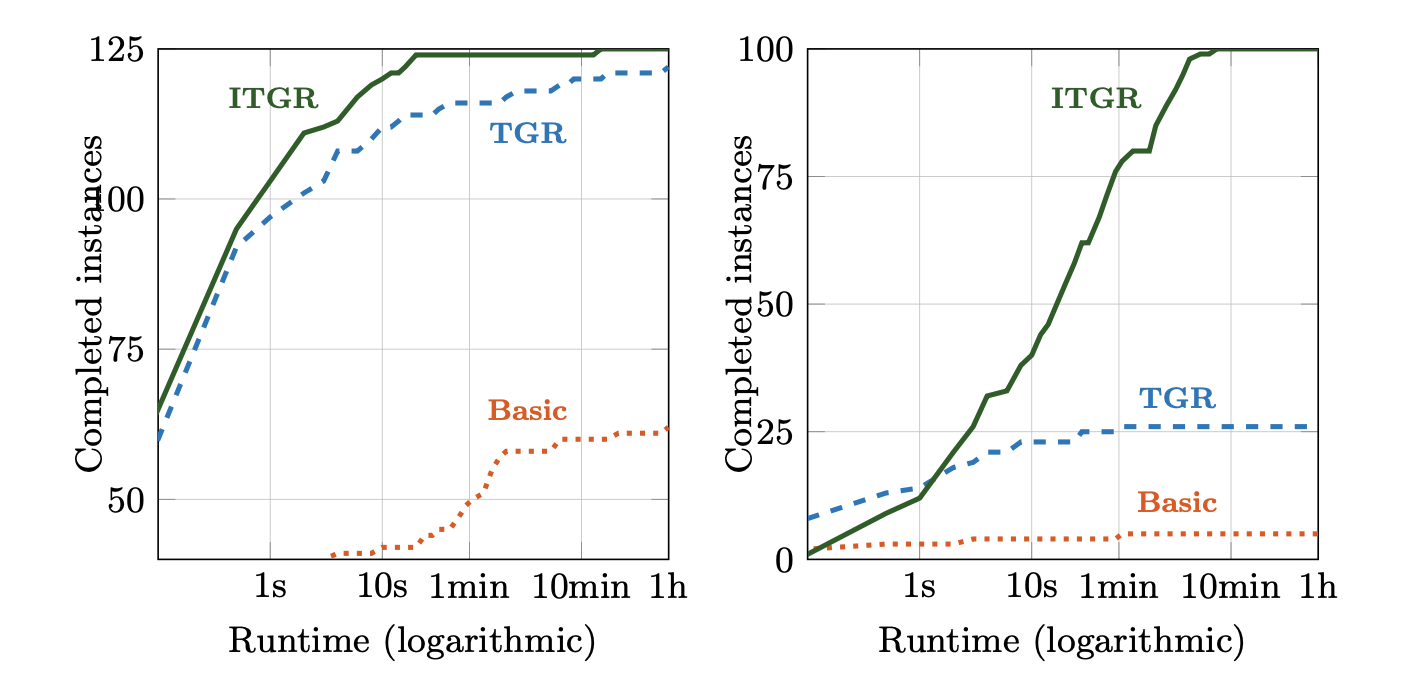
Plus another 100 models with 2^1000 only!
  • General reduction principle for directed graphs.
  • Transition guided reduction: Prunes states based on fireable transition labels.
  • Interleaving: Improve performance and stability by performing multiple reductions simultaneously.
  • Evaluation: Large real-world and generated Boolean networks.

Interleaved Transition Guided Reduction