Deep Implicits
with Differential Rendering
Daniel Yukimura
scene
parameters
2D image
- camera pose
- geometry
- materials
- lighting
- ...


rendering
differentiable
Feedback
(Learning)
Differentiable Volumetric Rendering

Can we infer implicit 3D representations without 3D supervision?
Differentiable Volumetric Rendering


single-view 3D reconstruction
Architecture

Forward Pass - Rendering:
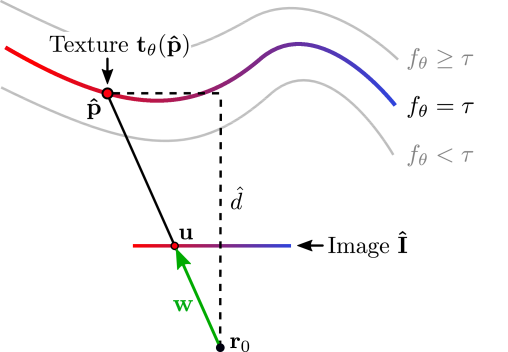
Backward Pass - Gradients:
Loss function
Differentiable Rendering
KNOWN
??
Depth Gradients:
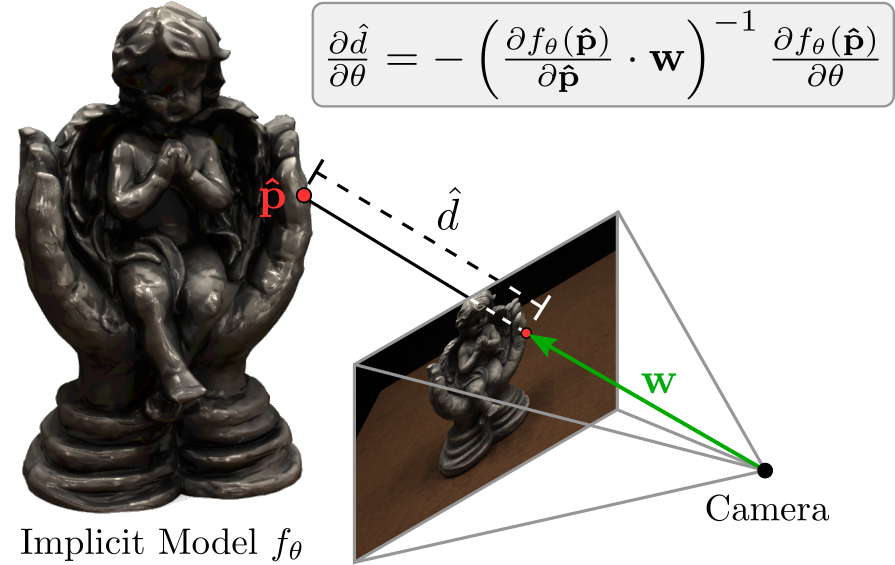
Single-View Reconstruction:
- Multi-View Supervision
- Single-View Supervision



Experiments:
Multi-View Reconstruction:
Experiments:
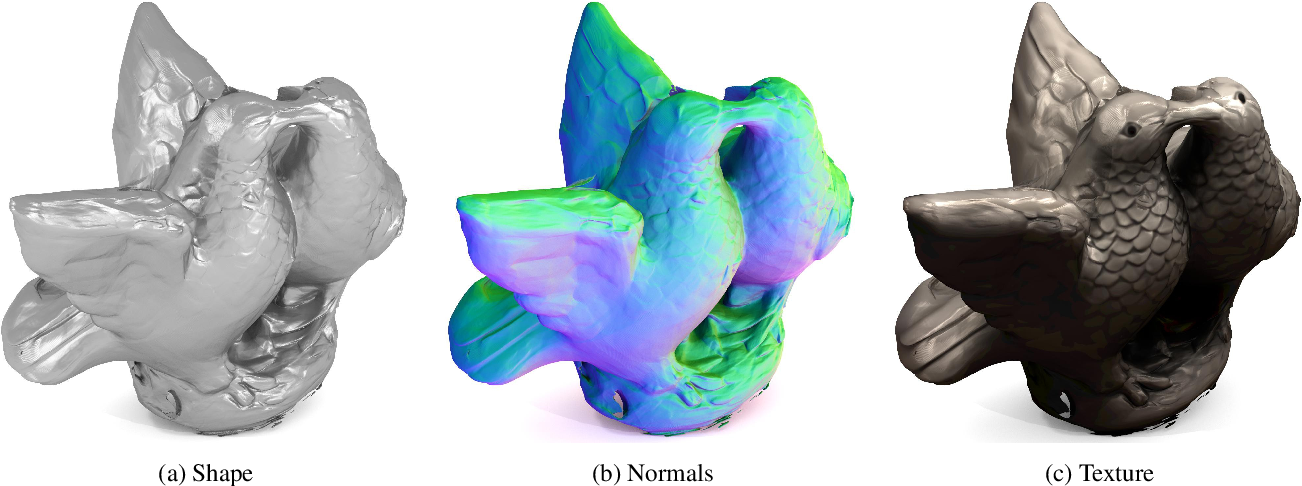
Implicit Differentiable Rendering
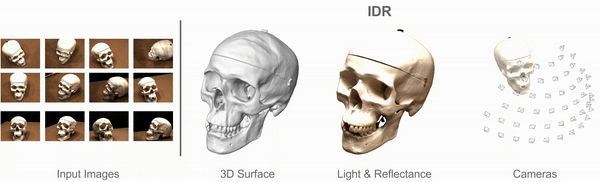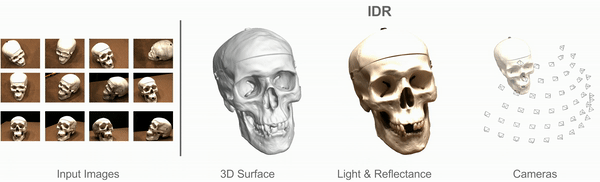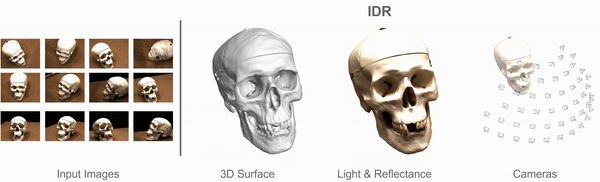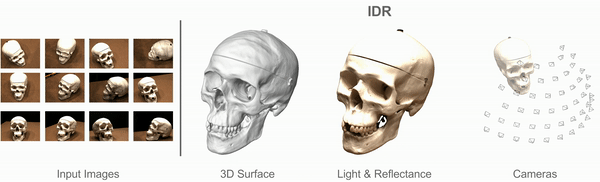
Multiview 3D Surface Reconstruction
Input: Collection of 2D images (masked)
with rough or noisy camera info.
Targets:
- Geometry
- Appearance (BRDF, lighting conditions)
- Cameras
Method:
Geometry:
signed distance function (SDF) +
implicit geometric regularization (IGR)

- geometry parameters
IDR - Forward pass

- camera parameters
Ray cast:
(first intersection)
IDR - Forward pass
- appearance parameters
Output (Light Field):
Surface normal
Global gometry feature vector

Differentiable intersections
Lemma:
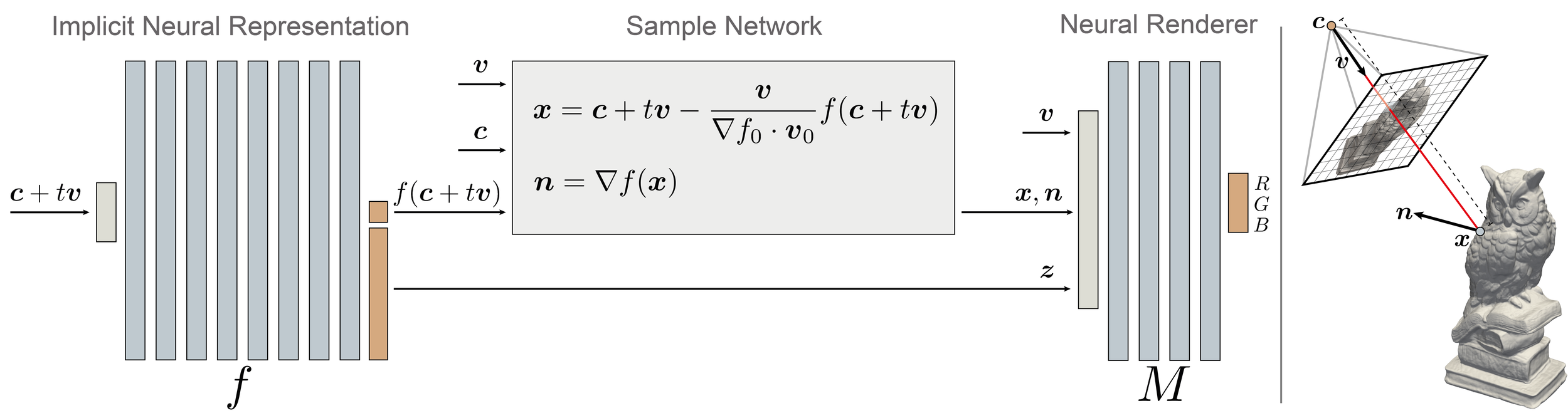
Light Field Approx.
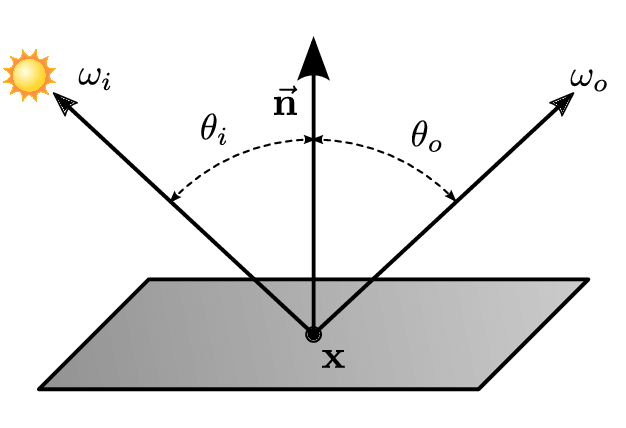
BRDF function
out direction
income direction
emitted
radiance
incoming radiance

Experiments:
Multi-View Reconstruction:
Experiments:
Disentangling Geometry and Appearance:
