Redes neurais profundas:

aspectos matemáticos e estatísticos

Roberto

Imbuzeiro

Oliveira

O que faz uma rede neural profunda?

https://code.fb.com/ml-applications/advancing-state-of-the-art-image-recognition-with-deep-learning-on-hashtags/,https://blog.webcertain.com/machine-translation-technology-the-search-engine-takeover/18/02/2015/, https://www.smithsonianmag.com/innovation/google-ai-deepminds-alphazero-games-chess-and-go-180970981/

Fonte: Szegedy Zaremba Sutskever Bruna Erhan Goodfellow Fergus (2013) e https://www.pymnts.com/innovation/2019/autonomous-vehicles-run-into-serious-roadblocks/

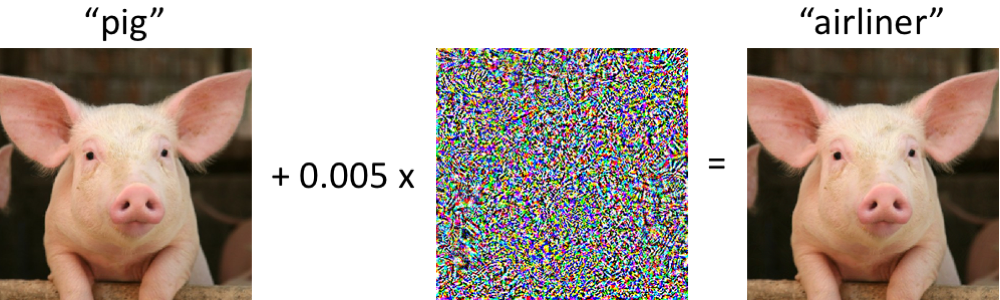
Uma família de algoritmos por trás de tudo.

Rede neural profunda

  • Entrada
  • Saída
  • "Neurônios": lugares onde computações são feitas
  • "Pesos sinápticos": parâmetros do modelo.

Perceptron (Rosenblatt'58)

\[ \sigma(x;w,a,b) = a \phi(w.x + b) \]

 

onde \(x\in\R^d\) é a entrada (vetor),

\(\phi:\R\to\R\) é função não-afim fixa

e \(w\in\R^d\), \(a\in\R\) , \(b\in \R\) são pesos.

 

Perceptron (Rosenblatt'58)

\[ \sigma(x;w,a,b) = a \phi(w.x + b) \]

 

Exemplos de \(\phi\):

  • \(\phi(t) = \frac{e^t}{1+e^t}\) sigmóide
  • \(\phi(t) = \max\{t,0\}\) ReLU

Intuição

\(x_1\)

\(x_1\)

\(x_2\)

\(x_3\)

Entrada

\(x_3\)

\(w_1\)

\(w_1\)

\(w_2\)

\(w_3\)

\(a,b\)

Pesos

\(a\phi(x_1w_1 + x_2w_2 + x_3w_3 + b)\)

Saída

Rede profunda (DNN)

Fonte: https://towardsdatascience.com/training-deep-neural-networks-9fdb1964b964

Tipos de neurônios

 

  • Conexões completas com neurônios anteriores.
  • Convoluções com pedaços da entrada/imagem, seguidas de funções não lineares (ConvNet).
  • "Pooling" de janelas pequenas...

 

Literatura empírica é IMENSA

Aprendender pesos?

 

  • Rede calcula função a partir da entrada com pesos como parâmetros: \[(x,\theta)\in\R^d\times \R^N\mapsto \widehat{y}(x;\theta).\]
  • Perda: \[\widehat{L}_n(\theta):=\frac{1}{n}\sum_{i=1}^n(Y_i - \widehat{y}(X_i;\theta))^2.\]
  • Como escolher \(\theta\) para minimizar perda?

Descida de gradiente

 

 

\[\theta^{(k+1)} = \theta^{(k)} - \alpha^{(k)}\nabla_\theta\widehat{L}_n(\theta^{(k)})\]

 

"Backpropagation" (Hinton): regra da cadeia compacta para calcular o gradiente.

Funciona?

Tudo indica que sim.

Redes com \(O(10^1)\) - \(O(10^2)\) camadas.

\(O(10^7)\) ou + neurônios por camada.
Bases de dados: ImageNet tem \(O(10^9)\) imagens.

Método exige potência computacional e muitos ajustes.

Por quê?

Ninguém sabe.

Descobrir isso é um objetivo de pesquisa de muitos.

Aplicações potenciais?

Performance no CIFAR-10

Taxa de erro desceu de 21% para 1%.

E agora?

 

  • Principais conferências dobram de tamanho a cada ano.
  • Indícios de que Inteligência computacional substituirá humanos em várias tarefas.
  • Pouquíssima compreensão teórica.

Como formular o problema?

Aprendizado Estatístico

 

Artigo relevante: Leo Breiman.

"Statistical Modeling: The Two Cultures"

Statistical Science v. 16, issue 3 (2001), 199 -231

Aprendizado supervisionado (regressão)

  • É dada uma função \(f:\R^d\times \Theta\to\R\).
  • Objetivo é escolher \(\theta\in \Theta\) de modo a minimizar o erro médio quadrático:

\[L(\theta):= \mathbb{E}_{(X,Y)\sim P}(Y-f(X;\theta))^2.\]

  • Aprendizado "estatístico" porque  \((X,Y)\in\R^d\times \R\) são aleatórios.

Dados e erro empírico

 

Na prática, não se sabe calcular a esperança, mas temos dados independentes e identicamente distribuídos.

\[(X_1,Y_1),(X_2,Y_2),\dots,(X_n,Y_n)\sim P.\]

 

Problema: como e o quanto o quanto podemos nos aproximar de um \(\theta\) ótimo? Quando isso é bom o suficiente?

Dados e erro empírico

 

Ideia: trocar a minimização do valor esperado pela minimização do "erro empírico".

 

\[\widehat{L}_n(\theta):= \frac{1}{n}\sum_{i=1}^n(Y_i-f(X_i;\theta))^2.\]

 

Chame de \(\widehat{\theta}_n\) o minimizador deste erro.

Por que pode dar certo?

 

Lei dos grandes números: se \(n\) é grande,

\[ \frac{1}{n}\sum_{i=1}^n(Y_i-f(X_i;\theta))^2 \approx \mathbb{E}_{(X,Y)\sim P}(Y-f(X;\theta))^2 \]

\[\Rightarrow \widehat{L}_n(\theta)\approx L(\theta).\]

 

É necessário um teorema sobre convergência uniforme: Vapnik, Chevornenkis, Dudley, Talagrand...

Viés e variância

 

Viés: se \(\Theta\) é "pequeno", pode ser que todas as escolhas de parâmetro tenham erro \(\mathbb{E}(Y-f(X;\theta))^2\) grande.

 

Variância: se \(\Theta\) é "muito grande", o erro na lei dos grandes números pode ser grande e isso complica a vida. 

Underfitting e overfitting

Visão tradicional: overfitting \(\approx\) interpolação

Fonte: https://hackernoon.com/memorizing-is-not-learning-6-tricks-to-prevent-overfitting-in-machine-learning-820b091dc42

Balanço de viés e variância

Teoria tem falhas para as DNNs

Boa notícia: viés pequeno

 

Suponha \[Y=f_*(X) + \text{ruído}\] com \(f_*\) contínua, então redes neurais com 1 camada interna com \(N\to +\infty\) neurônios têm viés \(\to 0\).

 

Kurt Hornik (1991) "Approximation Capabilities of Multilayer Feedforward Networks", Neural Networks, 4(2), 251–257

Descida de gradiente minimiza?

Interpolação

 

Teoria tradicional diz que variância vem capacidade de interpolar.

DNNs são capazes de interpolar quando têm muitos parâmetros e parecem funcionar mesmo assim.

Zhang et al, "Understanding deep learning requires rethinking generalization." ICLR 2017

Aprendizado c/interpolação

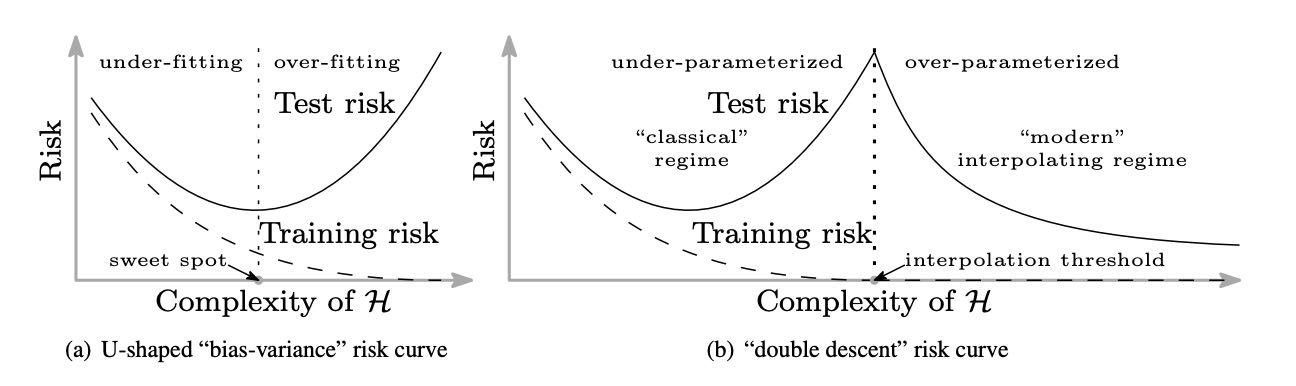
Source: https://arxiv.org/abs/1812.11118

Belkin, Hsu, Ma & Mandal (2018)

Não otimiza

Não adianta aplicar uma teoria baseada na minimização do erro empírico.

Falta de convexidade é a razão.

O que parece garantir convergência na prática?

Interpola

Medidas tradicionais de variância são inúteis.

Como medir variância?

Por que o "overfitting" não parece ser sempre um problema?

Min local

Teoria para métodos/estimadores que convergem para mínimos locais. 

(Arora, Ge, Jordan, Ma, Loh, Wainwright, etc)

Interpolação

É possível encontrar métodos que interpolam e têm bons resultados em alguns casos.

(Rakhlin, Belkin, Montanari, Mei, Bartlett, etc)

Problema: nada disso é sobre redes neurais.

Hipóteses de trabalho


  1. Devemos pensar em DNNs com infinitos parâmetros ("tamanho não importa").
  2. No limite de infinitos parâmetros, problema é "otimizável"
  3. O próprio método de descida de gradiente está ajudando para que tudo funcione.


Evidências: Zhang et al ICLR 2017.

DNNs: algum progresso

Uma primeira ilustração

 

  • Dada \(h:\R^{d_{in}}\times \R^D\to \R^{d_{out}}\) e medida de probabilidade sobre \(\R^D\), escreva:

\(h(x,\mu):= \int\,h(x,\theta)\,d\mu(\theta).\)

 

  • Uma rede neural profunda calcula composições de funções deste tipo, com medidas \(\mu\) diferentes para cada camada.
  • Aprendizado = as \(\mu\) evoluem no tempo.

Nossas redes

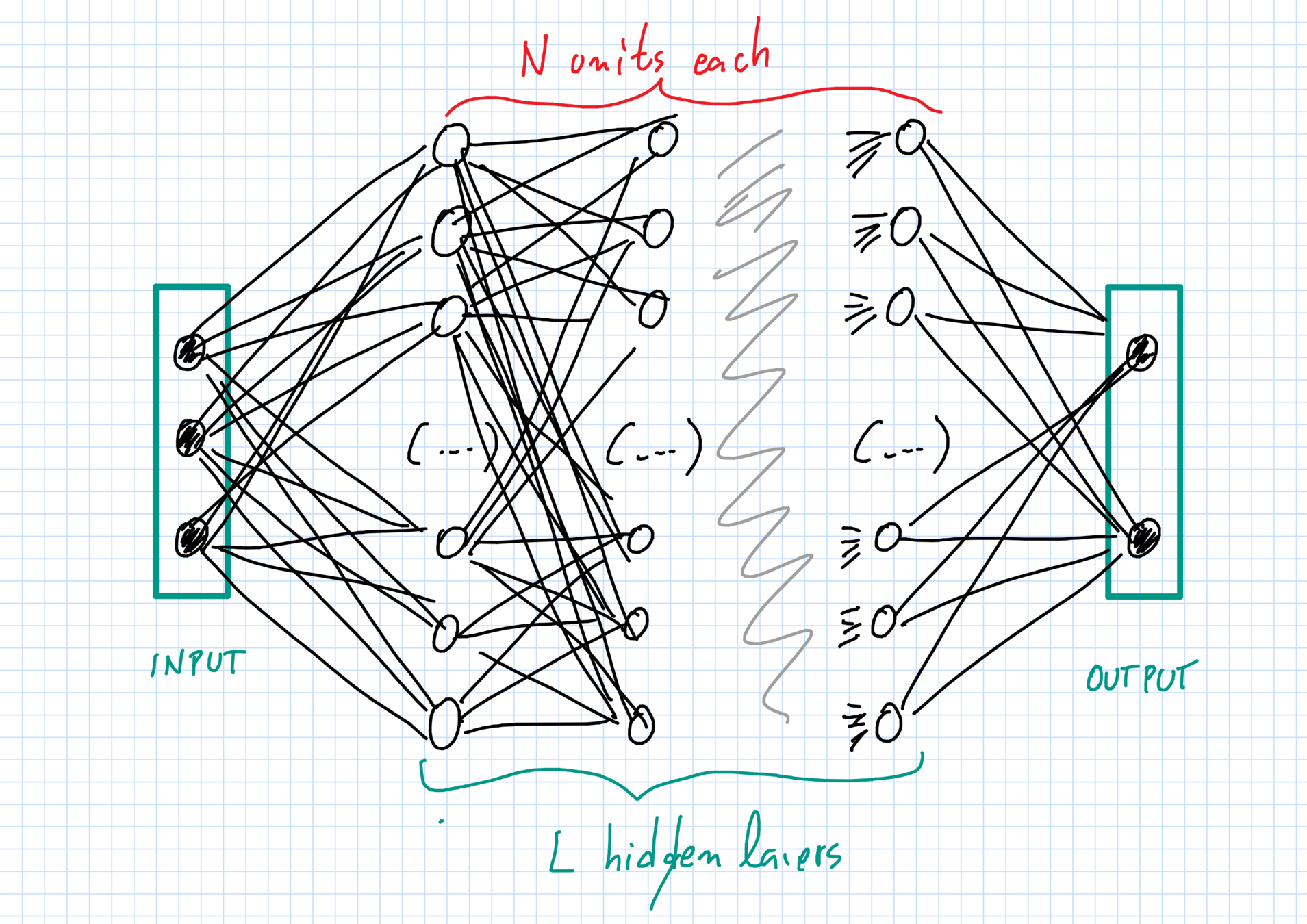
Pesos iniciais são aleatórios e independentes.

Nossas redes

Pesos iniciais são aleatórios e independentes.

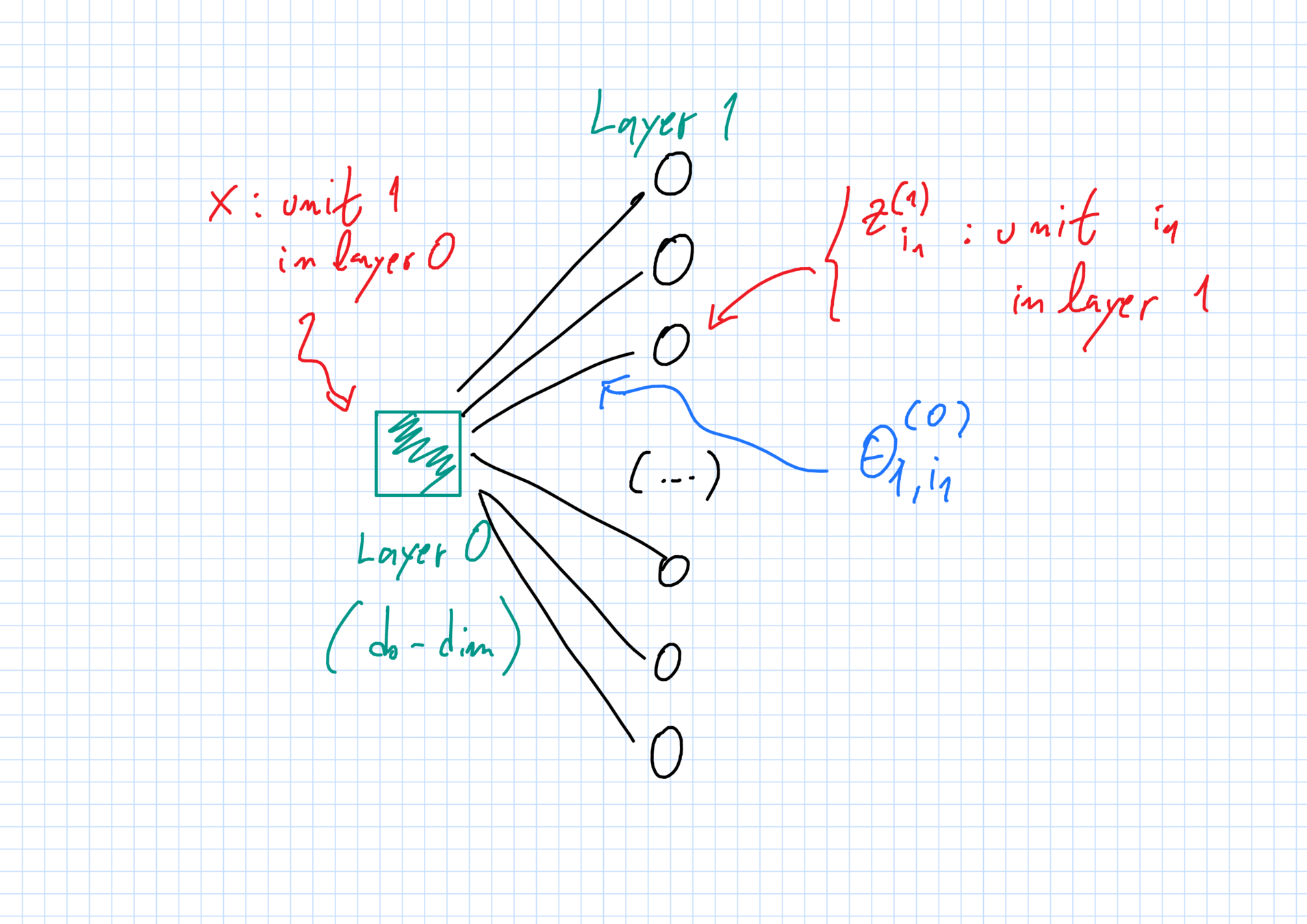
Camadas e unidades

Camadas \(\ell=0,1,\dots,L,L+1\):

  • \(\ell=0\) input e \(\ell=L+1\) output;
  • \(\ell=1,\dots,L\) camadas ocultas.

 

Cada camada \(\ell\) tem \(N_\ell\) unidades com dimensão \(d_\ell\).

  • \(N_0 = N_{L+1}=1\), (um input \(+\) um output);
  • \(N_\ell=N\gg 1 \) neurônios nas ocultas (\(1\leq \ell\leq L\)).

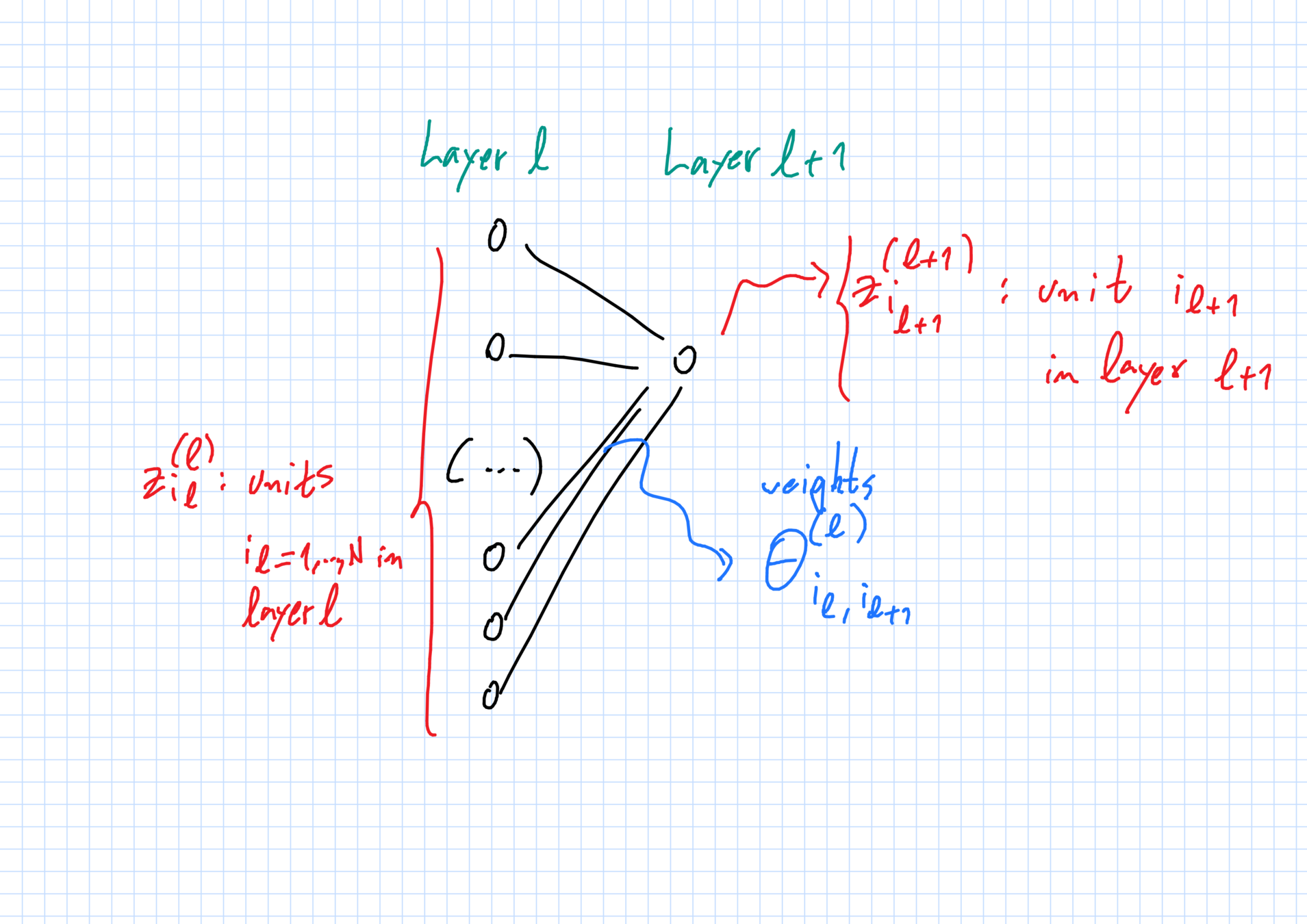
Pesos

"Pesos"  \(\theta^{(\ell)}_{i_\ell,i_{\ell+1}}\in\mathbb{R}^{D_\ell}\):

  • conecta unidade \(i_\ell\) na camada \(\ell\) \(\to\) unidade \(i_{\ell+1}\) na camada \(\ell+1\).

 

Vetor de todos os pesos: \(\vec{\theta}_N\).

 

Inicialização aleatória independente: mesmo superescrito \(\Rightarrow\) mesma lei \(\mu^{(\ell)}_0\).

 

Primeira camada oculta

z^{(1)}_{i_1}(x,\vec{\theta}_N):= \sigma^{(0)}_*(x,\theta^{(1)}_{1,i_1})

Camada \(\ell \to \ell+1\)

z^{(\ell+1)}_{i_{\ell+1}}(x,\vec{\theta}_N):= \frac{1}{N_\ell}\sum_{i_\ell=1}^{N_\ell}\sigma^{(\ell)}_*(z^{(\ell)}_{i_\ell}(x,\vec{\theta}_N),\theta^{(\ell)}_{i_\ell,i_{\ell+1}})

Função e perda

z^{(L+1)}_{1}(x,\vec{\theta}_N):= \frac{1}{N_L}\sum_{i_L=1}^{N_L}\sigma^{(L)}_*(z^{(\ell)}_{i_\ell}(x,\vec{\theta}_N),\theta^{(L)}_{i_L,i_{1}})

Na saída \(L+1\), \(N_{L+1}=1\).

\widehat{y}(x,\vec{\theta}_N) := \sigma^{(L+1)}_*(z^{(L+1)}_1(x,\vec{\theta}_N))
L_N(\vec{\theta}_N):= \frac{1}{2}\mathbb{E}_{(X,Y)\sim P}\,\|Y - \widehat{y}(X,\vec{\theta}_N)\|^2

Evolução dos pesos via SGD

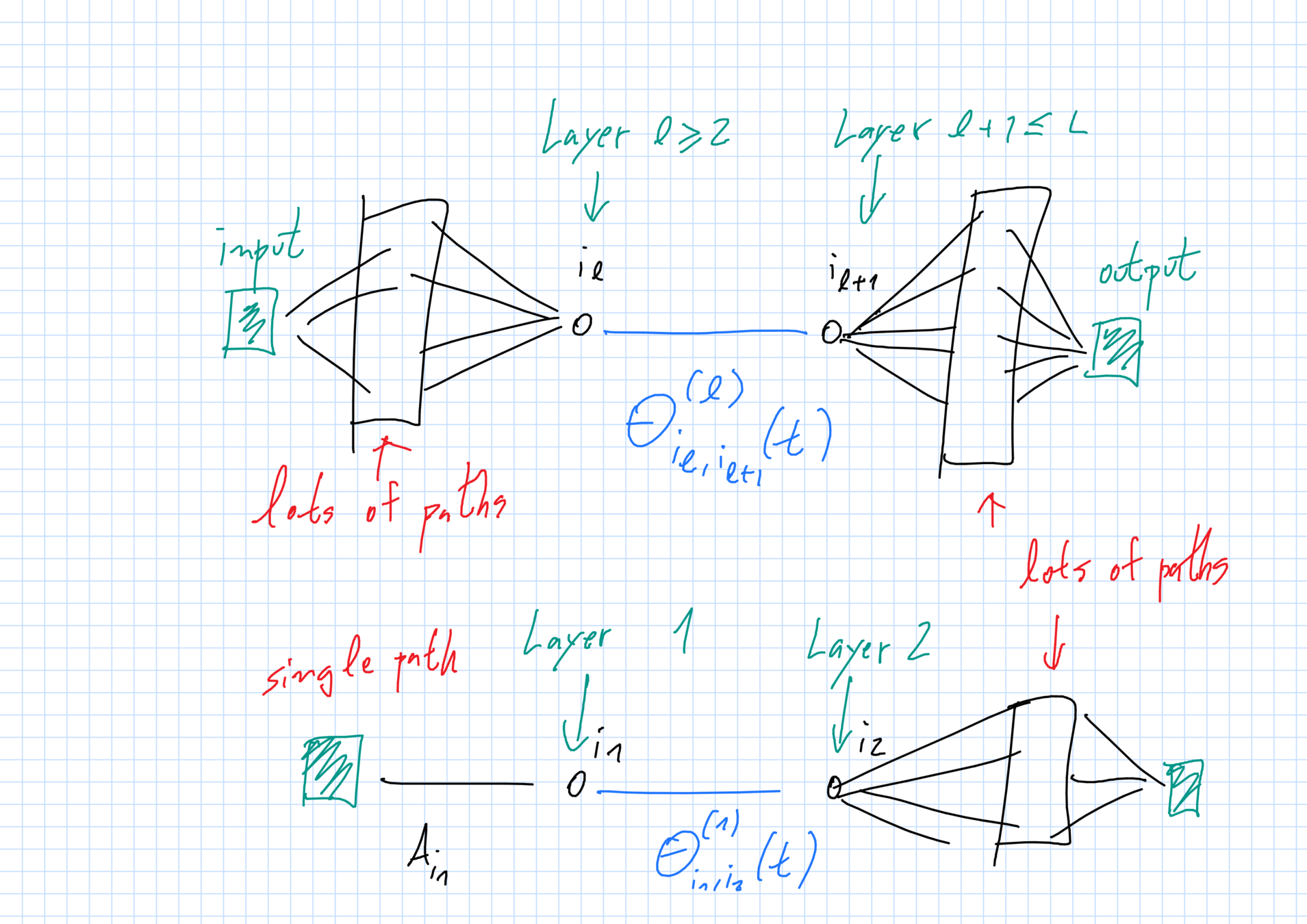
Pesos perto da entrada \(A_{i_1}:=\theta^{(0)}_{1,i_1}\) ou perto da saída \(B_{i_L}:=\theta^{(L)}_{i_L,1}\) ficam fixos ("random features").

 

Outros pesos \(\theta^{(\ell)}_{i_\ell,i_{\ell+1}}\) (\(1\leq \ell\leq L-1)\): SGD com tamanho de passo \(\epsilon\) e amostras "frescas" a cada passo.

Se \(\epsilon\ll 1\), \(N\gg 1\):

\[\frac{d}{dt}\vec{\theta}_N(t) \approx -N^2\, \nabla L_N(\vec{\theta}_N(t))\]

(\(N^2\) passos de SGD \(\sim 1\) 1 unid tempo no limite)


 

Comportamento limite com

\(N\to+\infty, \epsilon\to 0\)

Estrutura de dependências

Distribuição \(\mu_t\) dos pesos-limite

\[(A_{i_1},\overline{\theta}^{(1)}_{i_1,i_2}(t),\overline{\theta}^{(2)}_{i_2,i_3}(t),\dots,\overline{\theta}^{(L)}_{i_L,i_{L+1}}(t),B_{i_{L+1}})\sim \mu_t\]

 

fatoriza da seguinte forma:

\[\mu_t = \mu^{(0,1)}_t\otimes \mu^{(2)}_t \otimes \dots \otimes \mu_{t}^{(L-1)}\otimes \mu_t^{(L,L+1)}.\]

 

Pesos independentes em \(\ell\neq 1,L-1\), mas \(\theta^{(1)}_{i_1,i_2}\) depende de \(\theta^{(0)}_{1,i_1}\) (e mais nada)  e \(\theta^{(L-1)}_{i_{L-1},i_L}\) depende de \(\theta^{(L)}_{i_L,1}\) (e mais nada).  

Função limite e rede

\left\{\begin{array}{lll}\overline{z}^{(2)}(x,\mu_t)&:= & \int\,\sigma_*^{(1)}(\sigma_*^{(0)}(x,a),\theta)\,d\mu_t^{(0,1)}(a,\theta);\\ \\ {\rm For}\; \ell=3,\dots,L: & & \\ \overline{z}^{(\ell)}(x,\mu_t)&:= & \int\,\sigma_*^{(\ell-1)}(\overline{z}^{(\ell-1)}(x,\mu_t),\theta)\,d\mu_t^{(\ell-1)}(\theta);\\ \\ \overline{y}(x,\mu_t) &:=& \int\,\sigma_*^{(L+1)}(\sigma_*^{(L)}(\overline{z}^{(L)}(x,t),\theta),b) d\mu_t^{(L,L+1)}(\theta,b).\end{array}\right.

Função \(\widehat{y}(x,\vec{\theta}_N(t))\) é aprox. composição de funções da forma \(\int\,h(x,\theta)\,d\mu(\theta)\). 

\[L_N(\vec{\theta}_N)\approx \frac{1}{2}\mathbb{E}_{(X,Y)\sim P }\,\|Y - \overline{y}(X,\mu_t)\|^2\] onde

 

De onde isso vem?

Evolução limite dos pesos

Forma da evolução depende dos próprios pesos, das "densidades" de vizinhos numerosos e (para \(\ell=1,L\)) pesos próximos.

\left\{\begin{array}{lll}\dot{\theta}^{(1)}_{i_1,i_2}(t) &= &\psi^{(1)}(\theta^{(1)}_{i_1,i_2}(t),A_{i_1},\mu_t); \\ \\ {\rm For}\;2\leq \ell\leq L-2: \\ \dot{\theta}^{(\ell)}_{i_\ell,i_\ell+1}(t) &= &\psi^{(1)}(\theta^{(\ell)}_{i_\ell,i_{\ell+1}}(t),\mu_t); \\ \\ \dot{\theta}^{(L-1)}_{i_{L-1},i_L}(t) &= &\psi^{(L-1)}(\theta^{(L-1)}_{i_{L-1},i_L}(t),B_{i_L},\mu_t). \end{array}\right.

Lei dos grandes números

McKean-Vlasov 

Ansatz:

 

  1. Qualquer termo que é uma média de muitos pesos deve convergir a uma integral determinística com uma certa densidade.
  2. As densidades só devem depender da camada do peso.

 

\(\Rightarrow\) Processo de McKean-Vlasov.

McKean Vlasov?

McKean-Vlasov abstrato

\left\{\begin{array}{lll}Z(0)&\sim & \mu_0\,\\ \dot{Z}(t)&=& \psi(t,Z(t),\mu_t) + \sigma \dot{B}_t\,\,(t\geq 0)\\ \end{array}\right.

Considere:

  1. \(M_1(\mathbb{R}^D)\) = todas as medidas de prob. sobre \(R^D\),
  2. medidas \(\mu_t\in M_1(\mathbb{R}^D)\) for \(t\geq 0\);
  3. nível de ruído \(\sigma\geq 0\);
  4. função de deriva \(\psi:\mathbb{R}\times \mathbb{R}^D\times M_1(\mathbb{R}^D)\to \mathbb{R}^D\);
  5. Trajetória aleatória:

Auto-consistência: \(Z(t)\sim \mu_t\) for all times \(t\geq 0\)

O que representa

  • Nuvem de partículas indistinguíveis com distribuição espacial \(\mu_t\).
  • \(Z(t)\) = uma partícula típica na nuvem.
  • Campo médio: \(Z(t)\) interage com a média sobre a nuvem (=média sobre \(\mu_t\)).
  • Como \(Z(t) \) é típica, \(Z(t)\sim \mu_t\).

Existência e unicidade

\left\{\begin{array}{lll}Z(0)&\sim & \mu_0\,\\ \dot{Z}(t)&=& \psi(t,Z(t),\mu_t) + \sigma \dot{B}_t\,\,(t\geq 0)\\ \end{array}\right.

Sob condições tipo Lipschitz, para qualquer medida inicial \(\mu_0\) existe uma única trajetória

\[t\geq 0\mapsto \mu_t\in M_1(\mathbb{R}^D)\]

tal que qualquer processo 

satisfaz a condição de consistência de McKean-Vlasov:

\[Z(t)\sim \mu_t, t\geq 0.\]

[McKean'1966, Gärtner'1988, Sznitman'1991, Rachev-Ruschendorf'1998,...]

EDP descreve a densidade

\left\{\begin{array}{lll}Z(0)&\sim & \mu_0\,\\ \dot{Z}(t)&=& \psi(t,Z(t),\mu_t) + \sigma \dot{B}_t\,\,(t\geq 0)\\ \end{array}\right.

Densidade \(p(t,x)\) de \(\mu_t\) evolui de acordo com uma EDP não-linear.

\partial_t p(t,x) = \frac{\sigma^2}{2}\Delta_x p(t,x) + \nabla_x\cdot (\psi(t,x,\mu_t)\,p(t,x))

não-linearidade vem de \(\mu_t\sim p(t,x)\)

Feito para redes com \(L=1\)

  • Mei, Montanari e Nguyen
  • Rotskoff e van den Einjden
  • Sirignano e Spiliopoulos

 

arXiv 2018

Mei - Montanari - Nguyen

Função calculada pela rede

\[\widehat{y}(x,\vec{\theta}_N) = \frac{1}{N}\sum_{i=1}^N\sigma_*(x,\theta_i).\]

 

Perda:\[L_N(\vec{\theta}_N):=\frac{1}{2}\mathbb{E}_{(X,Y)\sim P}(Y-\widehat{y}(X,\vec{\theta}_N))^2\]

Mei - Montanari - Nguyen 

Evolução de um peso ("partícula"):

\dot\theta_i(t)\\ = -\gamma \,\int\,\,\left\{[y- (\widehat{\mu}_{N,t}\,\sigma_*(x,\cdot))]\, \partial_\theta\sigma_*(x,\theta_i(t))\right\}\,dP(x,y) \\ = \psi(\theta_i(t),\widehat{\mu}_{N,t})

onde \[\widehat{\mu}_{N,t}:= \frac{1}{N}\sum_{i=1}^N \delta_{\theta_i(t)}.\]

Heurística

Se vale a lei dos grandes números,

\[\widehat{\mu}_{N,t}\to \mu_t\] com \(\mu_t\) determinística. Logo no limite:

\dot\theta_i(t) = \psi(\theta_i(t),\mu_t)

Em particular, independência no tempo 0 é preservada

 

Tipicalidade: \(\theta_i(t)\sim \widehat{\mu}_{N,t}\approx \mu_t\).

Estrutura da EDP

A EDP neste caso

\partial_t p(t,x) = \frac{\sigma^2}{2}\Delta_x p(t,x) + \nabla_x\cdot (\psi(t,x,\mu_t)\,p(t,x))

corresponde a uma

descida de gradiente com potencial convexo no espaço de medidas de probabilidade sobre \(\R^D\).

 

Ambriosio, Gigli, Savaré, Figalli, Otto, Villani...

E o nosso caso?

As dependências limites dos pesos são muito complicadas.

 

  • Antes: unidades de análise = pesos individuais.

Mantêm-se i.i.d. no limite \(N\gg 1\). 

  • Nosso caso: unidades básicas são caminhos.

Não são i.i.d. no limite. Problema McK-V é descontínuo: aparecem probabilidades condicionais no limite. 

Lei dos grandes números

Como é a prova

 

Existência e unicidade do processo McK-V \((\mu_t)_{t\geq 0}\) que deve corresponder à distribuição limite de pesos ao longo de um caminho.

 

Provar que esta medida tem a estrutura certa de independência.

\[\mu_{[0,T]} = \mu^{(0,1)}_{[0,T]}\otimes \mu^{(2)}_{[0,T]} \otimes \mu_{[0,T]}^{(L-1)}\otimes \mu_{[0,T]}^{(L,L+1)}.\]

Usar essa estrutura

 

Dá para comparar os pesos reais e "partículas ideias" derivadas de \(\mu(t)\) através de argumentos de acoplamento.

A estrutura de dependências é fundamental neste passo.

A EDP limite é mais ou menos assim

 

[Public domain/Wikipedia]

Uma direção de pesquisa

 

No limite, o que uma DNN do nosso tipo faz é calcular composições de funções:

\(x\mapsto h(x;Q):= \int\,h(x,\xi)\,dQ(\xi)\) onde \(Q\in M_1(\mathbb{R}^{D})\).

  • Tomando as medidas \(Q\) como parâmetros, como é o problema de aprendizado/regressão neste espaço?
  • Qual é o melhor que dá para fazer?
  • DNNs são discretização disso. Há outras? Qual a melhor?

Obrigado!