Causal Inference for Software Traceability

int i = a \ b

assert ( i == a \ b )

Requirement

Terminology

Software Traceability is the way how we follow the implementation of a requirement by establishing relations among artifacts (e.g., design documents, bug reports, code)

int i = a \ b

assert ( i == a \ b )

Requirement

Source Code

Test Cases

Most of the state-of-the-art approaches for automated traceability recovery are based on Information Retrieval

Mining concepts from code with Topic Models (Linstead et al, 2007)

Latent Dirichlet Allocation (Maskeri et al, 2008)

VSM, LDA, Jensen-Shanon, Latent Semantic Indexing and Orthogonality (Oliveto et al, 2010)

Orthogonality and Hybrid Methods (Gethers et al, 2011)

Integrating multiple source of information and TM+GA (Dit et al, 2013)

Directed Acyclic Graph (DAG) is a finite directed graph with no directed cycles

A confounder is a variable that influences both the dependent variable and independent variable causing spurious association

Z

X

Y

X (independent variable) and Y (dependent variable) are not confounded iff the following holds:

P(y|do(x)) = P(y|x)

To estimate the effect of X on Y

Controlling for confounders

P(y|do(x)) \neq P(y|x)

P(y|do(x)) = \sum_{z} P(y|x,z)P(z)

P(Y=recovered | do(x=giveDrug)) =

Z

X

Y

Gender

Recovery

Drug

P(Y=recovered | do(x=giveDrug)) =

Z

X

Y

Gender

Recovery

Drug

P(Y=recovered|X=giveDrug,Z=male)P(Z=male) +

P(Y=recovered | do(x=giveDrug)) =

Z

X

Y

Gender

Recovery

Drug

P(Y=recovered|X=giveDrug,Z=male)P(Z=male) +

P(Y=recovered|X=giveDrug,Z=famale)P(Z=famale)

A Counterfactual is a conditional containing an if-clause which is contrary to fact (Goodman, 1947)

If the doctor did not give the drug, then the patient was not recovered

If the doctor had not given the drug, then the patient would not have been recovered

A Counterfactual is a conditional containing an if-clause which is contrary to fact (Goodman, 1947)

If the doctor did not give the drug, then the patient was not recovered

If the doctor had not given the drug, then the patient would not have been recovered

Pr[Y=1|A=1] - Pr[Y=1|A=0] = 0

A Counterfactual is a conditional containing an if-clause which is contrary to fact (Goodman, 1947)

If the doctor did not give the drug, then the patient was not recovered

If the doctor had not given the drug, then the patient would not have been recovered

Pr[Y=1|A=1] - Pr[Y=1|A=0] = 0

Pr[Y^{a=1}=1] - Pr[Y^{a=0}=1] = 0

Conditional Independence: learning the value of Y does not provide additional information about X, once we know Z

(X \perp Y|Z)

Conditional Independence: learning the value of Y does not provide additional information about X, once we know Z

The sets X and Y are said to be conditionally independent given Z if

P(x|y,z) = P(x|z)

(X \perp Y|Z)

Causal Effect vs Causal Inference

Causal Effect (in a nutshell)

Consider a dichotomous treatment A (1: LSI, 0:VSM) and a dichotomous outcome Y (1:Linked, 0:Not Linked)

Y^{a=1}

Observable Outcome Variables

read Y under treatment a = 1

Y^{a=0}

read Y under treatment a = 0

Causal Effect (in a nutshell)

Potential outcomes or counterfactual outcomes.

Y^{a=1} = 0

Consider this scenario for a specific Req R1 to Code C1

R1 is not Linked to C1 under LSI

Y^{a=0} = 1

R1 is Linked to C1 under VSM

Causal Effect (in a nutshell)

The treatment A has a causal effect on an individual's outcome Y if

Y^{a=1} = 0

Consider this scenario for a specific Req R1 to Code S1

Y^{a=0} = 1

Y^{a=1} \neq Y^{a=0}

Consider this powerful Research Question:

What is the average causal effect of IR baseline techniques on traceability?

In this case we need the expectation of the population

E[Y^{a=1}] \neq E[Y^{a=0}]

Pr[Y^{a=1}=1] \neq Pr[Y^{a=0}=1]

Measure of Causal Effect: Null Causal Effect

Pr[Y^{a=1}=1] - Pr[Y^{a=0}=1] = 0

Pr[Y^{a=1}=1] / Pr[Y^{a=0}=1] = 1

Inductive Causation (IC) Algorithm (Pearl, 1988)

Input: p a sampled distribution on a set T of variables
Output: some pattern (partially directed graph) compatible with p

Inductive Causation (IC) Algorithm (Pearl, 1988)

Based on variable dependencies
Find all pairs of variables that are dependent of each other
Eliminate indirect dependencies
Determine directions of dependencies

Inductive Causation (IC) Algorithm (Pearl, 1988)

X

Z

Y

Inductive Causation (IC) Algorithm (Pearl, 1988)

X

Z

Y

X

Z

Y

Inductive Causation (IC*) Algorithm (Pearl, 1988)

w

z

y

x

Inductive Causation (IC*) Algorithm (Pearl, 1988)

w

z

y

x

w

z

y

x

Inductive Causation (IC*) Algorithm (Pearl, 1988)

w

z

y

x

Inductive Causation (IC*) Algorithm (Pearl, 1988)

w

z

y

x

z

y

x

Experimental vs Observational

Software Traceability Observational or Experimental?

Automatic Repair Observational or Experimental?

Software Traceability Observational or Experimental?

Traceability Problem, the similarity values allow us to "observe" a correlation among artifacts

Similarity \approx Correlation

R

S

In experimental studies, we are allowed to change the individual.

To tackle the Traceability Problem by looking for correlations

Since we observe the phenomenon of traceabilty, it cannot be claimed that a Requirement Links are "Causing" Source Code Links

Similarity \neq Causation

R

S

How can we measure the causal effect?

Randomized Experiments

From Observational to Experimental

Inductive Traceability Causation

A software traceability link is a probability distribution of an artifact respect to a set of artifacts of interest

L: Artifact_x \to S_{Artificts}

Links

T = Pr[l \in L]

Traceability Link

A Causal Model M is composed by a set of n stochastic variables

T_k;k\in \{1,...,n\}

Endogenous Variables

U_{k'};k'\in \{1,...,n\}

Exogenous Variables

For each variable T the model contains a function f such that

T_k = f_k(pa(T_k),U_k, \theta_k)

Set of parents

For each variable T the model contains a function f such that

T_k = f_k(pa(T_k),U_k, \theta_k)

Hidden causes

For each variable T the model contains a function f such that

T_k = f_k(pa(T_k),U_k, \theta_k)

Constant factors

The joint probability Pr({T}) can be decomposed in a Markov factorization (Pearl, 2009)

Pr(T_1,...,T_n) = \prod_{k=1}^{n} Pr(T_k|pa(T_k))

The joint probability Pr({T}) can be decomposed in a Markov factorization (Pearl, 2009)

Pr(T_1,...,T_n) = \prod_{k=1}^{n} Pr(T_k|pa(T_k))

Joint Distribution

The joint probability Pr({T}) can be decomposed in a Markov factorization (Pearl, 2009)

Pr(T_1,...,T_n) = \prod_{k=1}^{n} Pr(T_k|pa(T_k))

Conditional Independencies

Joint Distribution

A causal model M has an associated graphical representation called Causal Structure G(M)

Causal Structure of a set of variables T is a DAG in which each node corresponds to a distinct element of T, and each link represents direct functional relationship among the corresponding variables

directional separation or d-separation is the conditional independence criteria

T_j \bot_G T_{j'} | C

directional separation or d-separation is the conditional independence criteria

T_j \bot_G T_{j'} | C

Two nodes T and T' are d-separated by a set of C iff for every path between T,T' one of the following condition is fulfilled:

The path contains a non-collider T_k
The path contains a collider T_k which does not belong to C and T_k is not ancestor of an node C

A causal structure can be inferred from the set of conditional independencies present in an observed joint distribution

T_j \bot_G T_{j'} | C

A causal structure can be inferred from the set of conditional independencies present in an observed joint distribution

T_j \bot_G T_{j'} | C

X

Z

Y

X \bot Y | Z

X \bot Y | \emptyset

How can we derive a probability distribution for the traceability variables?

T_k = f_k(pa(T_k),U_k, \theta_k)

f_k \propto \Upsilon

Observational Correlation

Observational correlations

L \in \{R_1 \to C_1, R_1 \to C_2,R_1 \to C_3\}

Observational correlations

L \in \{R_1 \to C_1, R_1 \to C_2,R_1 \to C_3\}

VSM(R_1 \to C) = \alpha_{R_1 \to C}

JS(R_1 \to C) = \beta_{R_1 \to C}

Observational correlations

L \in \{R_1 \to C_1, R_1 \to C_2,R_1 \to C_3\}

VSM(R_1 \to C) = \alpha_{R_1 \to C}

JS(R_1 \to C) = \beta_{R_1 \to C}

V = [\alpha,\beta]

Correlation Vector

What do we use for categorical samples?

R_1 \to C_1

R_1 \to C_2

R_1 \to C_3

\emptyset

What do we use for categorical samples?

R_1 \to C_1

R_1 \to C_2

R_1 \to C_3

\emptyset

Pr[l=R_1 \to C_1]

Pr[l=R_1 \to C_2]

Pr[l=R_1 \to C_3]

Pr[l=\emptyset]

What do we use for categorical samples?

R_1 \to C_1

R_1 \to C_2

R_1 \to C_3

\emptyset

Pr[l=R_1 \to C_1]

Pr[l=R_1 \to C_2]

Pr[l=R_1 \to C_3]

Pr[l=\emptyset]

\alpha

\beta

\Omega \div |L|

Pr[]

What do we use for categorical samples?

R_1 \to C_1

R_1 \to C_2

R_1 \to C_3

\emptyset

Pr[l=R_1 \to C_1]

Pr[l=R_1 \to C_2]

Pr[l=R_1 \to C_3]

Pr[l=\emptyset]

\Omega(\alpha_{R_1 \to C_1} + \beta_{R_1 \to C_1}) \div 3

\Omega(\alpha_{R_1 \to C_2} + \beta_{R_1 \to C_2}) \div 3

\alpha

\beta

Pr[]

\Omega \div |L|

Generalization for multinomial

\alpha

\beta

\Omega

Pr[]

\Upsilon \sim Multinomial

\Upsilon = \sum_{l \in L} \Omega(v_\alpha + v_\beta) \div |L|

Traceability Causal Graph

T_{R_1 \to C}

T_{R_3 \to C}

T_{R_2 \to C}

Traceability Causal Graph: using interventions

T_{R_1 \to C}

T_{R_3 \to C}

T_{R_2 \to C}

Pr[T_{R_1 \to C}|do(T_{R_2 \to C} = R_2 \to C_1)]

Traceability Causal Graph

T_{R_1 \to C}

T_{R_3 \to C}

T_{R_2 \to C}

Pr[T_{R_1 \to C}|do(T_{R_2 \to C} = R_2 \to C_1)]

Case Study: LibEst

Req File	Source File	Correlation
RQ11	est_client_proxy.c	0.0573523792522

Req File	Source File	Correlation
RQ11	est_client_proxy.c	0.0573523792522

Finding the graph is the crux of the problem

R0

R1

R2

R5

R4

R3

[
('R0', 'R1', {'marked': False, 'arrows': ['R0']}), 
('R0', 'R2', {'marked': False, 'arrows': ['R0']}), 
('R1', 'R5', {'marked': False, 'arrows': []}), 
('R2', 'R4', {'marked': False, 'arrows': []}), 
('R3', 'R4', {'marked': False, 'arrows': []}]

R0

R1

R2

R5

R4

R3

[
('R0', 'R1', {'marked': False, 'arrows': ['R0']}), 
('R0', 'R2', {'marked': False, 'arrows': ['R0']}), 
('R1', 'R5', {'marked': False, 'arrows': []}), 
('R2', 'R4', {'marked': False, 'arrows': []}), 
('R3', 'R4', {'marked': False, 'arrows': []}]

R0

R1

R2

R5

R4

R3

[
('R0', 'R1', {'marked': False, 'arrows': ['R0']}), 
('R0', 'R2', {'marked': False, 'arrows': ['R0']}), 
('R1', 'R5', {'marked': False, 'arrows': []}), 
('R2', 'R4', {'marked': False, 'arrows': []}), 
('R3', 'R4', {'marked': False, 'arrows': []}]

R0

R1

R2

R5

R4

R3

[
('R0', 'R1', {'marked': False, 'arrows': ['R0']}), 
('R0', 'R2', {'marked': False, 'arrows': ['R0']}), 
('R1', 'R5', {'marked': False, 'arrows': []}), 
('R2', 'R4', {'marked': False, 'arrows': []}), 
('R3', 'R4', {'marked': False, 'arrows': []}]

R0

R1

R2

R5

R4

R3

[
('R0', 'R1', {'marked': False, 'arrows': ['R0']}), 
('R0', 'R2', {'marked': False, 'arrows': ['R0']}), 
('R1', 'R5', {'marked': False, 'arrows': []}), 
('R2', 'R4', {'marked': False, 'arrows': []}), 
('R3', 'R4', {'marked': False, 'arrows': []}]

R0

R1

R2

R5

R4

R3

Causal Inference for Software Traceability

Terminology

Software Traceability is the way how we follow the implementation of a requirement by establishing ​relations among artifacts (e.g., design documents, bug reports, code)

Most of the state-of-the-art approaches for automated traceability recovery are based on Information Retrieval

Directed Acyclic Graph (DAG) is a finite directed graph with no directed cycles

A confounder is a variable that influences both the dependent variable and independent variable causing spurious association

X (independent variable) and Y (dependent variable) are not confounded iff the following holds:

Controlling for confounders

A Counterfactual is a conditional containing an if-clause which is contrary to fact (Goodman, 1947)

A Counterfactual is a conditional containing an if-clause which is contrary to fact (Goodman, 1947)

A Counterfactual is a conditional containing an if-clause which is contrary to fact (Goodman, 1947)

Conditional Independence: learning the value of Y does not provide additional information about X, once we know Z

Conditional Independence: learning the value of Y does not provide additional information about X, once we know Z

Causal Effect vs Causal Inference

Causal Effect (in a nutshell)

Causal Effect (in a nutshell)

Causal Effect (in a nutshell)

Measure of Causal Effect: Null Causal Effect

Inductive Causation (IC) Algorithm (Pearl, 1988)

Inductive Causation (IC) Algorithm (Pearl, 1988)

Inductive Causation (IC) Algorithm (Pearl, 1988)

Inductive Causation (IC) Algorithm (Pearl, 1988)

Inductive Causation (IC*) Algorithm (Pearl, 1988)

Inductive Causation (IC*) Algorithm (Pearl, 1988)

Inductive Causation (IC*) Algorithm (Pearl, 1988)

Inductive Causation (IC*) Algorithm (Pearl, 1988)

Experimental vs Observational

Software Traceability Observational or Experimental?

Automatic Repair Observational or Experimental?

Software Traceability Observational or Experimental?

Traceability Problem, the similarity values allow us to "observe" a correlation among artifacts

To tackle the Traceability Problem by looking for correlations

Randomized Experiments

From Observational to Experimental

Inductive Traceability Causation

A software traceability link is a probability distribution of an artifact respect to a set of artifacts of interest

A Causal Model M is composed by a set of n stochastic variables

For each variable T the model contains a function f such that

Set of parents

For each variable T the model contains a function f such that

Hidden causes

For each variable T the model contains a function f such that

Constant factors

The joint probability Pr({T}) can be decomposed in a Markov factorization (Pearl, 2009)

The joint probability Pr({T}) can be decomposed in a Markov factorization (Pearl, 2009)

The joint probability Pr({T}) can be decomposed in a Markov factorization (Pearl, 2009)

Causal Structure of a set of variables T is a DAG in which each node corresponds to a distinct element of T, and each link represents direct functional relationship among the corresponding variables

directional separation or d-separation is the conditional independence criteria

directional separation or d-separation is the conditional independence criteria

A causal structure can be inferred from the set of conditional independencies present in an observed joint distribution

A causal structure can be inferred from the set of conditional independencies present in an observed joint distribution

How can we derive a probability distribution for the traceability variables?

Observational correlations

Observational correlations

Observational correlations

Correlation Vector

What do we use for categorical samples?

What do we use for categorical samples?

What do we use for categorical samples?

What do we use for categorical samples?

Generalization for multinomial

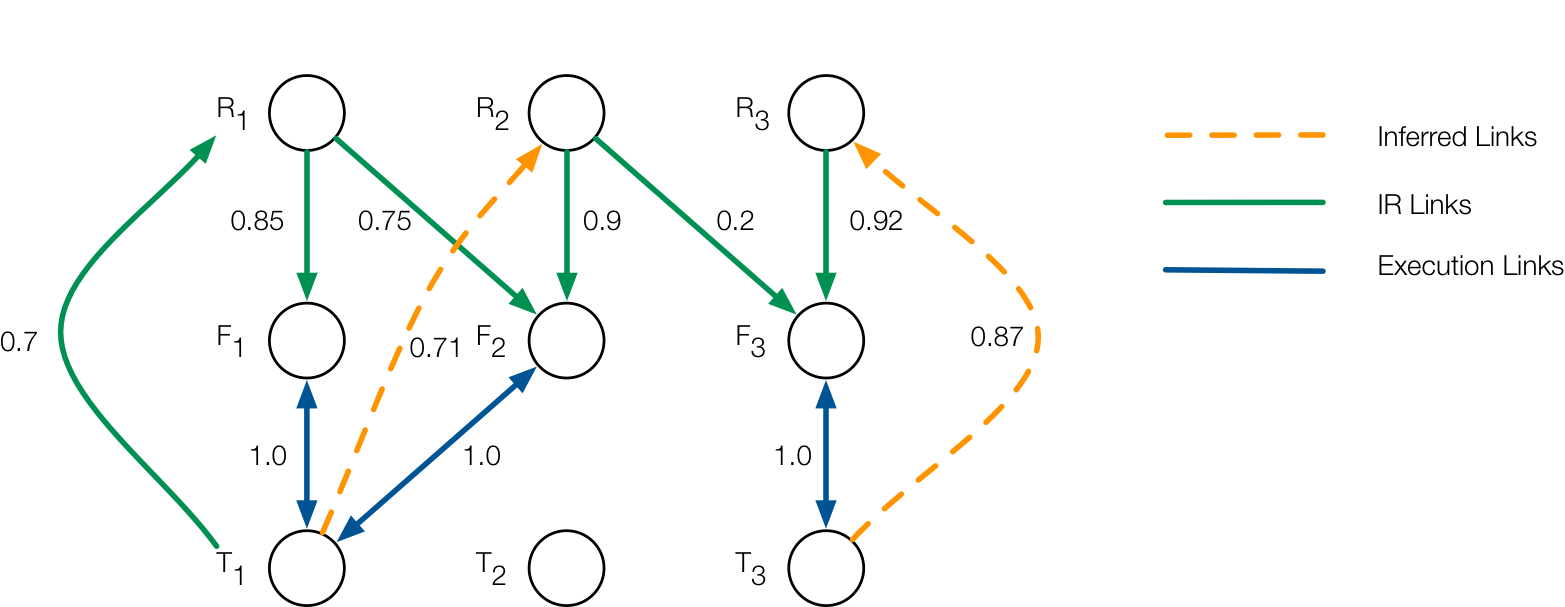
Traceability Causal Graph

Traceability Causal Graph: using interventions

Traceability Causal Graph

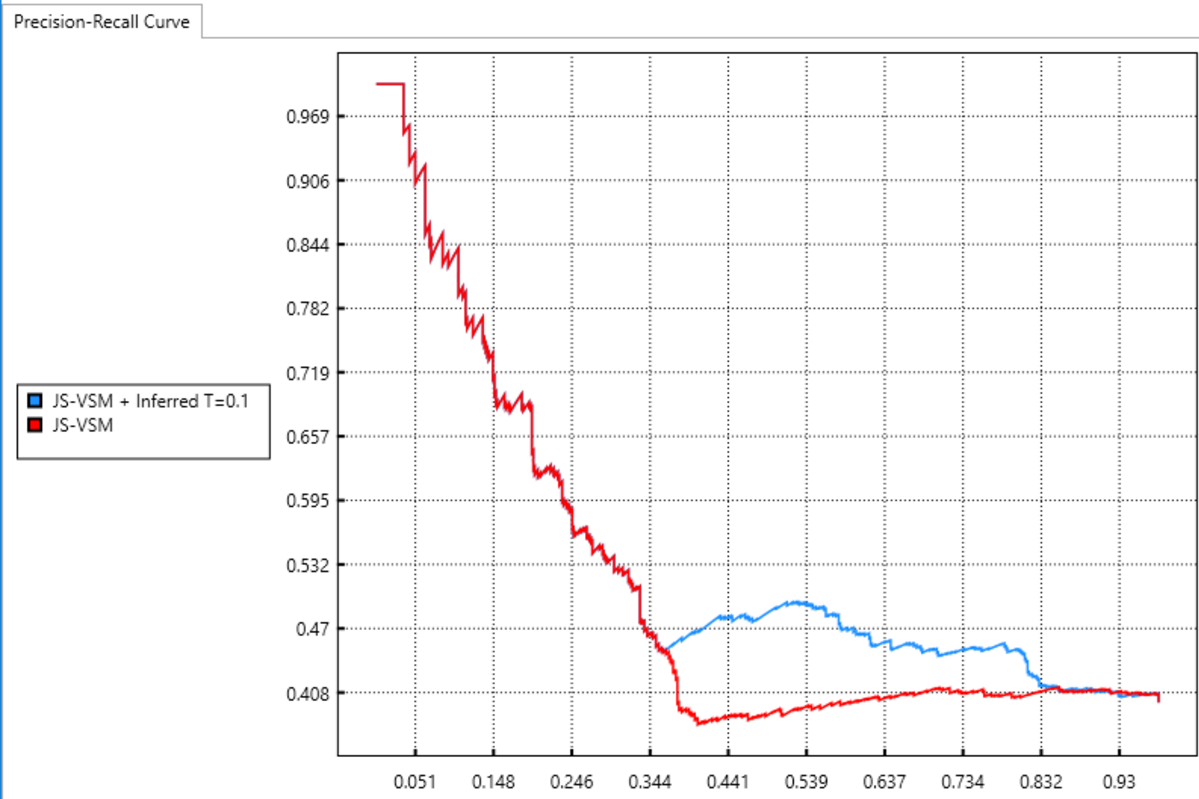
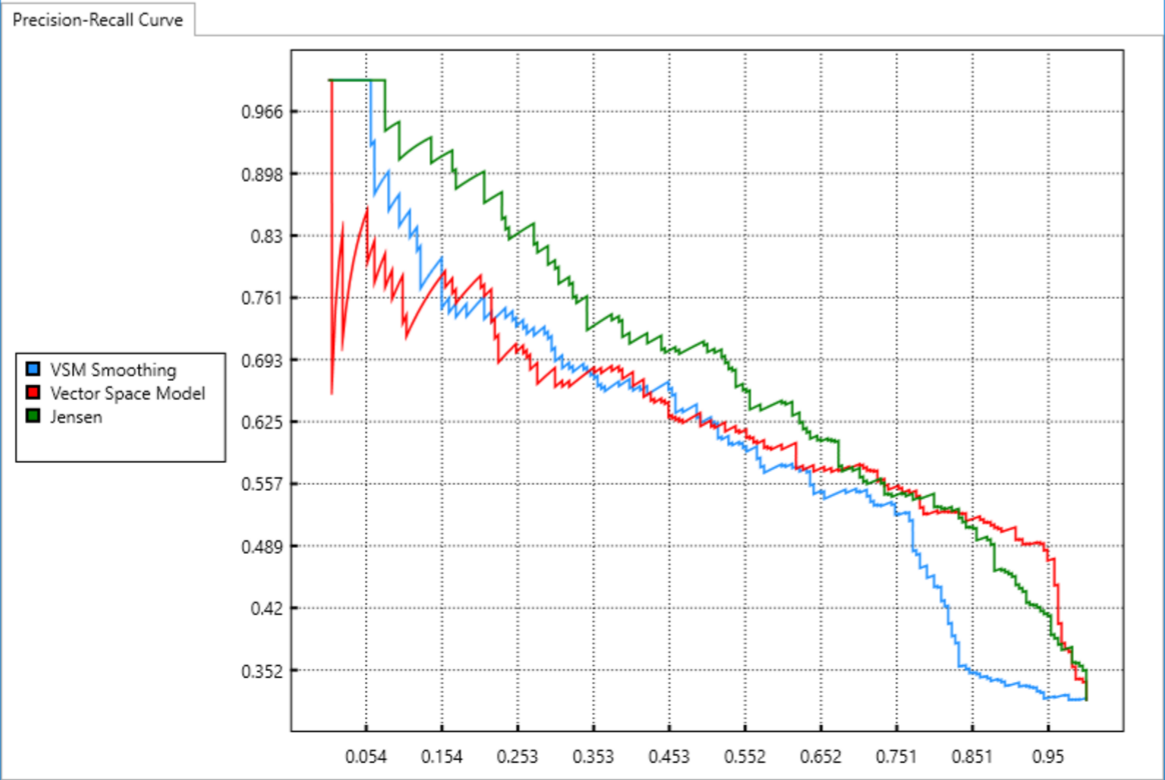
Case Study: LibEst

Finding the graph is the crux of the problem

Thank you

Software Traceability is the way how we follow the implementation of a requirement by establishing relations among artifacts (e.g., design documents, bug reports, code)