Asympt. složitost, Reprezentace grafů

LAB 01

B4M33PAL - Ing. David Pařil

Ing. David Pařil

Bývalý student Kybernetiky a robotiky ČVUT FEL

Lektor katedry kybernetiky

Výzkum v oblasti kardiologické chirurgie v Nizozemí

Organizátor Robotických táborů a Robosoutěží

Správce Bastlírny na strahově

Místnost: E-220

Kontakt: parildav@fel.cvut.cz

B4M33PAL

Maximálně 2 absence za semestr!

Podmínkou zápočtu je alespoň 24 bodů z DÚ.

Viz courseware předmětu...

COURSEWARE

Příklad

Big O” notace

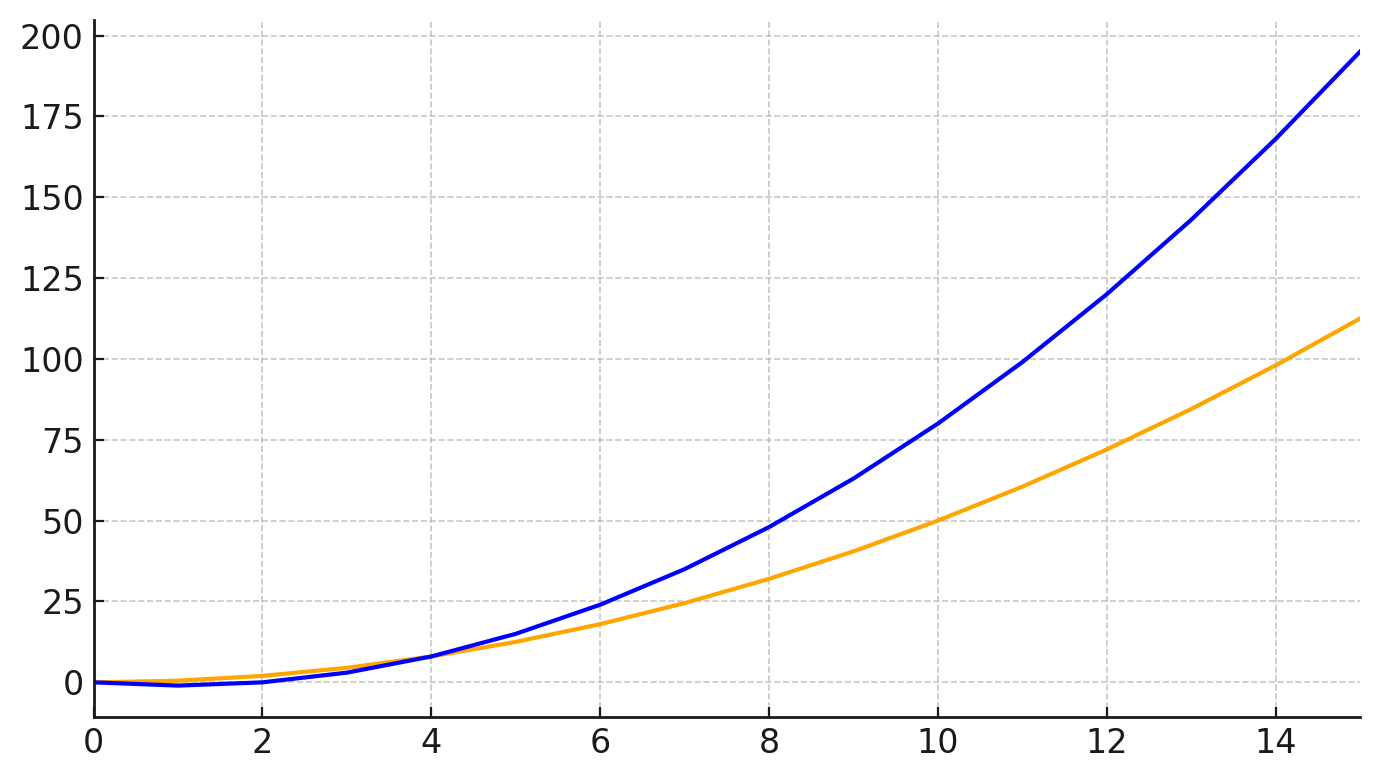
Ověřte, že platí:

Graf funkce $f(n) = 0.5n^2$ pro $n>4$ tedy leží vždy pod grafem funkce $g(n) = n^2 - 2n$ a navíc rozdíl g(n) - f(n) roste do nekonečna s rostoucím $n$.

Dokažte pomocí definice množiny $O(f(n))$, že i přesto platí:

$$g(n) \in O(f(n))$$

$$\forall n \in \mathbb{N}:\quad n>4 \quad \Rightarrow \quad n^{2}-2n > 0.5\,n^2$$

$$\quad n^{2}-2n > \frac{1}{2} \,n^2$$

$$-\frac{1}{2} \,n^2$$

$$\frac{1}{2}n^2-2n >0$$

$$n \left(\frac 1 2 n -2\right)>0$$

$$>0$$

Obě poloviny jsou v rozmezí $n>4$ striktně kladné $\rightarrow$ Důkaz

$$\forall n \in \mathbb{N}:\quad n>4 \quad \Rightarrow \quad \textcolor{blue}{n^{2}-2n} > \textcolor{orange}{0.5\,n^2}$$

Příklad

Růst Funkcí

Symbolem $\lg$ značíme logaritmus o základu 2.

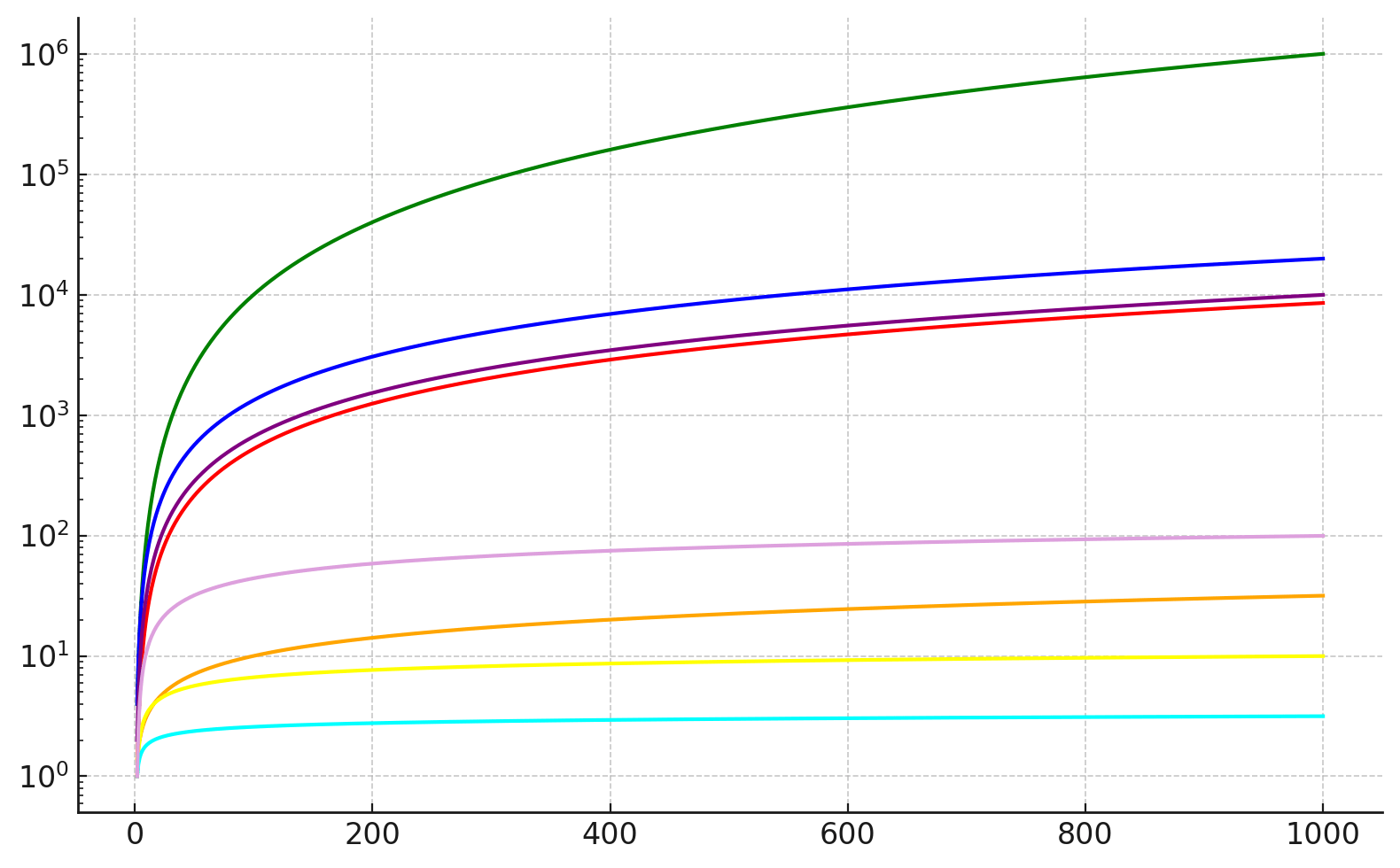
Uspořádejte podle řádu růstu uvedené funkce proměnné $n$.

Zdůvodněte pořadí každých dvou sousedních funkcí v tomto uspořádání.

$\lg(n!)$

$(\sqrt{2})^{\lg(n)}$

$2^{\lg(\lg(n))}$

$4^{\lg(n)}$

$\sqrt{\lg(n)}$

$n \lg(n^2)$

$n \lg(n)$

$ (\lg(n))^2$

Nápověda: potřebujeme se zbavit exponentů a faktoriálu.

Příklad

$\lg(n!)$

Jak se zbavit faktoriálu? Dá se to zjednodušit?

Existuje nějaký přibližný odhad $\lg(n!)$?

Stirlingův vzorec

= nejznámější aproximace faktoriálu pro vysoké hodnoty...

$$n! \approx \sqrt{2 \pi n}\left(\frac{n}{e}\right)^n$$

Příklad

$\lg(n!)$

Stirlingův vzorec

$$n! \approx \sqrt{2 \pi n}\left(\frac{n}{e}\right)^n$$

$\lg\left[ \sqrt{2 \pi n}\left(\frac{n}{e}\right)^n \right]$ = $\lg \sqrt{2 \pi n} + \lg\left(\frac{n}{e}\right)^n $

malé

$n\lg\left(\frac{n}{e}\right) \quad\rightarrow\quad e$ je zanedbatelné

$O\left(n\lg\left(n\right)\right)$

Příklad

$\lg(n!)$

Alternativní řešení:

Horní mez: $\lg k \leq \lg n$ pro všechna $k$, takže

$$\lg(n!) <= \sum^n_{k=1} \lg k = n \lg n \quad \rightarrow \quad \mathcal{O}(n \lg n)$$

Dolní mez: pro $k = \frac n 2 + 1, ..., n$ je $\lg k \geq \lg \frac n 2$ a takových členů je $\geq \frac n 2$

$$\lg(n!) \geq \frac n 2 \lg \frac n 2 = \frac n 2 (\lg n - \lg 2) = \Omega(n\lg n)$$

Získáváme tedy řešení $\Theta(n\lg n)$

$\lg(n!)$

$(\sqrt{2})^{\lg(n)}$

$2^{\lg(\lg(n))}$

$4^{\lg(n)}$

$\sqrt{\lg(n)}$

$n \lg(n^2)$

$n \lg(n)$

$ (\lg(n))^2$

$\Theta(n\lg n)$

$\left(2^{\frac 1 2}\right)^{\lg n}$

$\sqrt n$

$\lg n$

$2^{\lg n^2}$

$n^2$

$2^{2 \lg n}$

$2 n\lg n$

$n\lg n$

$\sqrt n$

$\lg n$

$n^2$

$\sqrt{\lg(n)}$

$2 n\lg n$

$n \lg(n)$

$ (\lg(n))^2$

$n\lg n$

$\sqrt n$

$\lg n$

$n^2$

$\sqrt{\lg(n)}$

$2 n\lg n$

$n \lg(n)$

$ (\lg(n))^2$

Nový

1

3

$\lg(n!)$

$(\sqrt{2})^{\lg(n)}$

$2^{\lg(\lg(n))}$

$4^{\lg(n)}$

$\sqrt{\lg(n)}$

$n \lg(n^2)$

$n \lg(n)$

$ (\lg(n))^2$

Pořadí

Původní

6

4

7

2

3

5

Příklad

Průchod polem

Algoritmus $A$ projde celým polem délky $N$ a prvek s indexem $k$ zpracuje za $ck$ milisekund. Konstanta $c$ je stále stejná.

Určete asymptotickou složitost zpracování celého pole.

Pole:

Prvek $k$

Zpracování $c \cdot k$ ms

Pole:

$c$

$2c$

$3c$

$Nc$

$+$

$\dotsm$

$+$

$$\frac{c + Nc}2 \cdot N$$

Průměrná hodnota × počet prvků

$\Theta(N^2)$

Příklad

Průchod maticí

Algoritmus $P$ projde celým 2D polem velikosti $N\times N$ a prvek na pozici $(k,m)$ zpracuje za:

A) $c(k+m)$ milisekund.

B) $c(km)$ milisekund.

Konstanta $c$ je stále stejná.

Určete asymptotickou složitost zpracování celého pole.

$k$

$m$

$k$

$m$

Varianta A) $c(k+m)$

Odhad: určitě musí být větší než $\Theta(N^2)$

$$ \sum_{k=1}^N \sum_{m=1}^N \textcolor{green}{c}(k+m) $$

$$ \sum_{m=1}^N k + \sum_{m=1}^N m $$

$$ N k + \frac{N+1}{2} N $$

$$ \textcolor{green}{c} \sum_{k=1}^N \left[ N k + \frac{N+1}{2} N \right]$$

$$ \textcolor{green}{c} \left( N \cdot \frac{N+1}{2} N + \frac{N+1}{2} N^2 \right)$$

$$ \textcolor{green}{c} \left( N+1 \right) N^2$$

$k$

$m$

Varianta B) $c(km)$

Odhad: jaký řád?

Přibližně horší o řád: $\approx \Theta(N^4)$

Přesné řešení: $c \cdot \frac {N^2}{4} (N+1)^2$

Příklad

Převody grafových reprezentací

Popiště jednotlivé reprezentace orientovaného grafu v paměti počítače které znáte. Pro každou možnou dvojici reprezentací R1 a R2 navrhněte pseudokód, který vzájemný převod provede, a určete, jaká bude jeho asymptotická složitost.

$n$ uzlů a $m$ hran

	a	b	c	d	e
a	0	1	0	1	0
b	1	0	1	0	1
c	0	1	0	0	1
d	1	0	0	0	1
e	0	1	1	1	0

Matice sousednosti

a
b
c
d
e

Seznam sousedů

$n$ uzlů a $m$ hran

	a	b	c	d	e
a	0	1	0	1	0
b	1	0	1	0	1
c	0	1	0	0	1
d	1	0	0	0	1
e	0	1	1	1	0

Matice sousednosti

a
b
c
d
e

Seznam sousedů

Matice -> Seznam

Seznam -> Matice

A ← n×n nuly
for u in 1..n:
  for v in adj[u]:
    A[u][v] ← 1

adj ← n prázdných seznamů
for u in 1..n:
  for v in 1..n:
    if A[u][v] = 1:
      append v to adj[u]

adj ← n prázdných seznamů
for u in 1..n:
  for v in 1..n:
    if A[u][v] = 1:
      append v to adj[u]

A ← n×n nuly
for u in 1..n:
  for v in adj[u]:
    A[u][v] ← 1

$\Theta(N^2)$

$\Theta(n+2m)$

Za předpokladu, že nemusíme alokovat paměť

... jinak $\Theta(N^2)$

Příklad

DFS/BFS se sekvenčním přístupem

Předpokládejte, že máte k dispozici neorientovaný graf $G = (V,E)$,

který je reprezentován seznamem hran.

Seznam hran není nijak uspořádán!

Přístup k jeho jednotlivým prvkům je pouze sekvenční (nelze přistupovat pomocí indexu).

Určete asymptotickou složitost BFS a DFS.

Přípomenutí:

Jaká je asymptotická složitost klasického BFS a DFS?

BFS(G, s):
  for v in V: visited[v] ← false
  Q ← empty queue
  visited[s] ← true
  enqueue(Q, s)
  while Q not empty:
    u ← dequeue(Q)
    for v in adj[u]:
      if not visited[v]:
        visited[v] ← true
        enqueue(Q, v)

DFS(G, s):
  for v in V: visited[v] ← false
  DFSvisit(s)

DFSvisit(u):
  visited[u] ← true
  for v in adj[u]:
    if not visited[v]:
      DFSvisit(v)

Správná odpověď: $\Theta(n + m)$

$n$ uzlů a $m$ hran

Neorientovaný graf $G = (V,E)$ je reprezentován seznamem hran.

$$ \langle v_1, v_4 \rangle, \langle v_2, v_5 \rangle, \langle v_2, v_6 \rangle, ...$$

Pro každý uzel musí být prozkoumán celý seznam hran:

$$O(\lvert V\rvert \cdot \lvert E\rvert)$$

Cvičení:

Mějme neorientovaný graf na 2D mřížce o velikosti $N \times N$. Určete, jak velký zásobník/fronta je potřeba alokovat pro BFS/DFS worst-case-scenario při dané konfiguraci?

start

cíl

start

cíl

start

cíl

BFS:

Počet uzlů jedné vrstvy je nejvýš $\Theta(N)$.

DFS:

Může jít přes všechny uzly bez návratu - v zásobníku drží celou cestu: $\Theta(N^2)$.

Příklad

Hledání minimální kostry

Napište pseudokód Jarníkova algoritmu, určete jeho časovou složitost a najděte pomocí něj minimální kostru následujícího grafu:

3

1

4

2

1 D

E

C

B

A

3

1

4

2

1 D

E

C

B

A

Prim / Jarník

Jarnik(G, start):
  for v in V:
    key[v] ← +∞
    parent[v] ← NIL
    inT[v] ← false

  key[start] ← 0
  H ← min-heap všech vrcholů podle key[·]

  while H není prázdný:
    u ← extract_min(H)          // nejmenší key
    inT[u] ← true               // u přidáme do stromu

    for (v, w_uv) in adj[u]:    // všechny hrany z u
      if not inT[v] and w_uv < key[v]:
        parent[v] ← u
        key[v] ← w_uv
        decrease_key(H, v, key[v])

  return { (parent[v], v) | v ∈ V \ {start} }